It often happens that we have to compare fractions with different numerators and different denominators.

For example, compare fractions and . To answer the question of which of these fractions is larger or smaller, you must reduce them to the same (common) denominator. Then you can easily determine which fraction is larger or smaller.

Let's reduce fractions and to the same (common) denominator. Find the least common multiple (LCM) of the denominators of both fractions. The LCM of the denominators of fractions and is 6.

The fractions that need to be compared are different. The best case is when the fractions have the same denominators, but different numerators. In this case, the following rule applies:

Of two fractions with the same denominators, the one with the larger numerator is larger. The fraction with the smaller numerator is smaller.

For example, compare fractions and and answer which of these fractions is larger. The denominators are the same, but the numerators are different. Fraction has a larger numerator than fraction . It means that is larger than . That's how we answer. Answer with the bigger sign (>).

The next case we can get into is when the numerators of the fractions are the same, but the denominators are different. The following rule is provided for such cases:

If we compare two fractions with identical numerators, the one with the smaller denominator is larger. And correspondingly smaller is the fraction whose denominator is larger.

You will often find an expression in which the division of fractions is written with a fractional dash. For example, the expression can be written as follows:

What is the difference between expressions and ? Actually, there is no difference. The two expressions have the same meaning and can be equated:

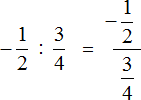
In the first case, the division sign is a colon and the expression is written on one line. In the second case, the division of fractions is written with a fractional dash. The result is a fraction, which is called a complex fraction.

Any mixed number is the result of isolating the whole part in an improper fraction. For example, consider an improper fraction . If you isolate the whole part of it, you get

But the reverse process is also possible: any mixed number can be converted into an improper fraction. To do this, multiply the whole part by the denominator of the fractional part and add the result to the numerator of the fractional part. The result will be the numerator of the new fraction, and the denominator will remain unchanged.

For example, let's convert a mixed number into an improper fraction. Multiply the whole part of 2 by the denominator of the fractional part:

An improper fraction is a fraction with a numerator greater than the denominator.

There are improper fractions that have 10, 100, 1000 or 10000 in the denominator. Such fractions can be converted to decimals. However, before converting to a decimal, the whole part of the fraction must be extracted.

Example 1. Convert an improper fraction into a decimal.

Fraction is an improper fraction. To convert such a fraction into a decimal, you must first select the whole part of the fraction. Recall how to select the whole part of improper fractions. If you forget, we suggest that you go back to this topic and study it thoroughly.

We know that if we want to convert a mixed number into an improper fraction, we need to multiply the integer part by the denominator of the fractional part and add it to the numerator of the fractional part. The resulting number will be the numerator of the new fraction, and the denominator remains the same.

For example, let's convert the mixed number to an improper fraction

Multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part:

(2 × 2) + 1

Let's calculate this expression:

(2 × 2) + 1 = 4 + 1 = 5

Any decimal can be converted back to a regular fraction. Again, to do this, it is enough to know how to read decimals. For example, translate 0.3 into an ordinary fraction. 0.3 is zero point three. Write down zero integers first:

0

and next to three tenths 0 . Zero is traditionally not written down, so the final answer is not 0, but just .

---

Example 2. Convert a decimal 0.02 into an ordinary fraction.

0.02 is zero integers and two hundredths. We do not write down zero, so we write down two hundredths

---

Example 3. Convert 0.00005 to a fraction

0.00005 is zero integers and five hundred thousandths. We do not write down zero, so we immediately write down five hundred thousandths

---

Example 4. Convert 3.5 to a fraction

First, convert the given decimal to a mixed number:

Now convert the mixed number to an improper fraction:

---

Example 5. Convert 1.25 to a fraction

First, convert the given decimal to a mixed number:

Now convert the mixed number to an improper fraction:

---

Video lesson

Any decimal can be converted back to a mixed number. To do this, all you need to know is how to read decimals.

For example, let's convert 6.3 to a mixed number. 6.3 is six integers and three tenths. Let's write down six integers first:

6

and next to three tenths:

---

Example 2. Convert a decimal 3.002 to a mixed number

3.002 is three integers and two thousandths. We first write down three integers

3

and next to it write down two thousandths:

3

Ordinary fractions with 10, 100, 1000 or 10000 in the denominator can also be converted to decimals. Since a fraction has no whole part, first write down 0, then put a dot and write down the numerator of the fractional part.

Here too, the number of zeros in the denominator and the number of digits in the numerator must be the same. Therefore, you should be careful.

Example 1. Convert an ordinary fraction into a decimal.

The whole part is missing, so first write 0 and put a dot:

0.

Now look at the number of zeros in the denominator. We see that there is one zero. And there is one digit in the numerator. So we can safely continue the decimal by writing the number 5 after the point