Definition. A mathematical expression is any combination of numbers, letters, and relational operators. We can say that all mathematics consists of expressions.
There are two kinds of expressions: numerical and alphabetical.
Numerical expressions consist of numbers and relational operators.
For example, the following expressions are numerical expressions:
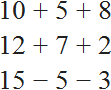
An expression with unknown contain letters in addition to numbers and relational operators. For example, the following expressions are the expressions with unknown:

Letters that are contained in letter expressions are called variables. Remember this once and for all! Ask any schoolboy what a variable is - this question will put him in a stupor, despite the fact that he will solve complex math tasks without knowing what it is. In the meantime, variable is a fundamental concept without an understanding of which mathematics cannot be studied.
By the word "study" we mean independent reading of the relevant literature and the ability to understand what is written there. Otherwise, it seems that you know mathematics with a B grade, you can solve some problems, but you cannot understand what is written in lectures and books. Everyone knows this feeling, especially students.
Since the understanding of a variable is very important, let's dwell on it in more detail. Look closely at the word "variable. Does it ring any bells? The word "variable" comes from the words "to change", "to change", "to change its value". A variable in mathematics is always expressed by some letter. For example, let's write the following expression:
a + 5
This is an expression with unknown. There is one variable - a. Because it is a variable, it can change its value at any time. Anyone can change the value: you, your teacher, your friend, anyone. For example, let's change the value of this variable. Let's give it the value 5. So let's write the variable itself, then let's make an equal sign and write 5
a = 5
What happens as a result of this? The value of the variable a (which is 5) will go into the main expression a + 5, and will be substituted for a.
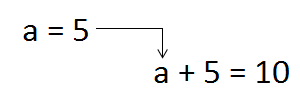
The value of the variable a is substituted into the original expression
The result is: 5 + 5 = 10
Of course, we have considered the simplest expressions. In practice, there are more complex expressions that contain fractions, powers, roots, and parentheses. This looks scary. But in fact, there's nothing to be afraid of. The main thing is to understand the principle.
In textbooks, you will often find the following problem: Find the value of the expression x + 10 if x = 5. Such an expression requires that you substitute the value of the variable for it. Let's do it. The value of the variable x is 5. Substitute that five into the original expression x + 10 and we get 5 + 10 = 15.
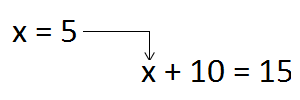
The value of the variable x is substituted into the expression x + 10
A variable is a kind of container where the value is stored. Variables are convenient because they allow you, without giving examples, to prove theorems, to write various formulas and laws.
Recall Lesson 2, Basic Operations. To understand what addition is, we gave the example 5 + 2 = 7, and said that the numbers 5 and 2 are the summands of, and the number 7 is the sum result. But we could have understood the topic without the example if we had used a letter expression. Denote the summands by any letters, for example a and b, and denote the sum result by c. Then we would have an expression with three variables a + b = c, and we would say that a and b are the summand and c is the sum.
So, having expression a + b = c, we can use it by substituting any numbers instead of variables a and b. And the variable c will get its value automatically, depending on what numbers we substitute instead of a and b
As practice you can do the following task. The expression a + b = c is given. Find its value if a = 10, b = 6. Variable c will get its value automatically. Write the answer as follows: If a = 10 and b = 6, the variable c is equal to ...
Solution:
a + b = c
10 + 6 = 16
Answer: when a = 10 and b = 6, the variable c is 16.
Result of the expression
In elementary school textbooks, you will often find the task to solve something, followed by a list of exercises. When you have an assignment like this in front of you, you should immediately understand what you need to calculate. This is often sounds like "solve an example", but if we are more literate, we should say "evaluate an algebraic expression". Solving an example and finding the value of an expression are actually the same thing.
For example, an expression 10 + 6 is given, and we are asked to find the value of that expression. This means that we need to solve this example. Put an equal sign = and write down the answer:
10 + 6 = 16
The resulting sum (16) is called the value of the expression 10 + 6.
Definition. The value of an expression is the result of the computation described by this expression when the variables and constants in it are assigned values
Let's look at some more examples:
- 16 is the value of the expression 4 × 4, because 4 × 4 = 16
- 20 is the value of the expression 10 + 10, because 10 + 10 = 20
- 5 is the value of the expression 10 ÷ 2, because 10 ÷ 2 = 5
Comments