Intersection of sets
Consider two sets: John's set of friends and Michael's set of friends.
John's Friends = {Tom,
Fred,
Max,
George }
Michael's Friends = { Leo,
Tom,
Fred,
Evan }
We see that Tom and Fred are both friends of John and Michael.
Talking in set terms, the elements Tom and Fred belong to both John's set of friends and Michael's set of friends.
Let's define a new set called "Common Friends of John and Michael" and add Tom and Fred to it as elements:
John and Michael's mutual friends = { Tom, Fred }
In this case, the set "Shared friends of John and Michael" is the intersection of the sets of John and Michael's friends.
An intersection of two (or more) original sets is a set that consists of elements belonging to each of the original sets.
In our case, the elements Tom and Fred belong to each of the original sets, namely, the set of John's friends and the set of Michael's friends.
Denote the set of John's friends by the letter A, the set of Michael's friends by the letter B, and the set of John and Michael's common friends by the letter C:
A = { Tom, Fred, Max, George }
B = { Leo, Tom, Fred, Evan }
C = { Tom, Fred }
Then the intersection of sets A and B will be set C and written as follows:
A ∩ B = C
The symbol ∩ means intersection.
When speaking of a set, we usually mean the elements belonging to that set. The intersection symbol ∩ reads as AND. Then the expression A ∩ B = C can be read as follows:
«Elements that belong to set A AND set B are elements that belong to set C».
Or even simpler:
«Friends belonging to John AND Michael at the same time, there are common friends of John and Michael».
Now suppose that John and Michael have no friends in common. For convenience, as before, we denote the set of John's friends by the letter A, and the set of Michael's friends by the letter B.
A = { Max, George }
B = { Leo, Evan }
In this case, the original sets are said to have no common elements and the intersection of such sets is an empty set. An empty set is denoted by the symbol ∅
A ∩ B = ∅
Example 2. Consider two sets: set A consisting of numbers 1, 2, 3, 5, 7 and set B consisting of numbers 1, 2, 3, 4, 6, 12, 18
A = { 1, 2, 3, 5, 7 }
B = { 1, 2, 3, 4, 6, 12, 18 }
Define a new set C and add to it elements that simultaneously belong to the set A and to the set B
C = { 1, 2, 3 }
The set C is the intersection of the sets A and B because the elements of the set C simultaneously belong to the set A and to the set B
Example 3. Consider two sets: the set A, consisting of the numbers 1, 5, 7, 9, and the set B, consisting of the numbers 1, 4, 5, 7
A = { 1, 5, 7, 9 }
B = { 1, 4, 5, 7 }
Define a new set C and add to it elements which simultaneously belong to the set A and to the set B
C = { 1, 5, 7 }
The set C is the intersection of the sets A and B because the elements of the set C simultaneously belong to the set A and the set B.
Example 4. Find the intersection of the following sets:
A = { 1, 2, 3, 7, 9 }
B = { 1, 3, 5, 7, 9}
C = { 3, 4, 5, 8, 9}
The intersection of the sets A, B, and C will be the set consisting of elements belonging to each of the sets A, B, and C. These elements are numbers 3 and 9.
Define a new set D and add elements 3 and 9 to it. Then use the intersection symbol ∩ to write that the intersection of sets A, B, and C is the set D
D = { 3, 9}
A ∩ B ∩ C = D
It is not necessary to define sets with letters to find the intersection. If there are few elements, the set can be specified by direct enumeration of elements.
For example, let the first set consist of elements 1, 3, 5, and the second set consist of elements 2, 3, 5. The intersection in this case is the set consisting of elements 3 and 5. To write the intersection, you can use direct enumeration:
{ 1, 3, 5 } ∩ { 2, 3, 5 } = { 3, 5 }
Numerical intervals, which we discussed in the previous lessons, are also sets. The elements of such sets are the numbers in the numerical interval.
For example, the interval [2; 6] can be understood as the set of all numbers from 2 to 6. For clarity, you can list all the integers belonging to this interval:
2, 3, 4, 5, 6 ∈ [2; 6]
Note that we have listed only integers. The segment [2; 6] also includes other numbers that are not integers, such as decimals. Decimals are placed between integers, but their number is so great that it is impossible to list them.
Another example. An interval (2; 6) can be understood as the set of all numbers from 2 to 6 except the numbers 2 and 6. We said earlier that an interval is a numerical interval whose boundaries do not belong to it. To make it clear, we can list all the integers that belong to the interval (2; 6):
3, 4, 5 ∈ (2; 6)
Since numerical intervals are sets, we can find intersections between different numerical intervals. Let's look at some examples.
Example 5. There are two numerical intervals: [2; 6] and [4; 8]. Find their intersection.
Both intervals have square brackets, so their boundaries belong to them.
For illustration, let us list all the integers that belong to the intervals [2; 6] and [4; 8]:
2, 3, 4, 5, 6 ∈ [2; 6]
4, 5, 6, 7, 8 ∈ [4; 8]
We see that numbers 4, 5, 6 belong both to the first interval [2; 6] and to the second one [4; 8].
Then the intersection of numerical intervals [2; 6] and [4; 8] is the numerical interval [4; 6]
[2; 6] ∩ [4; 8] = [4; 6]
Let us represent the intervals [2; 6] and [4; 8] on the coordinate line. On the upper area mark the numerical interval [2; 6], on the lower area mark the interval [4; 8].
![]()
We see that the numbers belonging to the interval [4; 6] belong both to the interval [2; 6] and to the interval [4; 8]. We can also see that the strokes belonging to the intervals [2; 6] and [4; 8] intersect in the interval [4; 6]. In such a situation, when there is a coordinate line in front of your eyes, the notion of intersection of sets can be understood in the direct sense, which is very convenient.
Example 6. Find the intersection of numerical intervals [-2; 3] and [4; 7].
Both intervals are framed by square brackets, so their boundaries belong to them.
For illustration, let us list all the integers that belong to the intervals [-2; 3] and [4; 7]:
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
4, 5, 6, 7 ∈ [4; 7]
We see that the numerical intervals [-2; 3] and [4; 7] have no common numbers. Therefore their intersection is an empty set:
[−2; 3] ∩ [4; 7] = Ø
If you draw the numerical intervals [-2; 3] and [4; 7]on the coordinate line, you can see that they do not intersect anywhere:

Example 7. A set of one element { 2 } is given. Find its intersection with the interval (-3; 4)
The set, consisting of one element { 2 }, on the coordinate line is represented as a filled circle, and the numeric interval (-3; 4) is an interval, the borders of which do not belong to it. So the boundaries of -3 and 4 will be represented as empty circles:
![]()
The intersection of the set { 2 } and the number interval (-3; 4) is the set consisting of one element { 2 }, because element 2 belongs to both the set { 2 } and the number interval (-3; 4)
{ 2 } ∩ (−3; 4) = { 2 }
In fact, we already dealt with the intersection of number spaces when we solved systems of linear inequalities. Recall how we solved them. First, we found the set of solutions to the first inequality, then the set of solutions to the second inequality. Then we found the set of solutions that satisfy both inequalities.
In fact, the set of solutions satisfying both inequalities is the intersection of the sets of solutions of the first and second inequalities. These sets are numeric intervals.
For example, to solve a system of inequalities 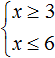 , we must first find the solution sets of each inequality, then find the intersection of these sets.
, we must first find the solution sets of each inequality, then find the intersection of these sets.
In this example, the solution of the first inequality x ≥ 3 is the set of all numbers that are greater than 3 (including the number 3 itself). In other words, the solution of the inequality is the numerical interval [3; +∞).
The solution of the second inequality x ≤ 6 is the set of all numbers that are less than 6 (including the number 6 itself). In other words, the solution of the inequality is the numerical interval (-∞; 6]
And the general solution of the system will be the intersection of the sets of solutions of the first and second inequalities, that is, the intersection of the numerical intervals [3; +∞) and (-∞; 6].
If we represent the set of solutions of the system 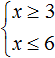 on the coordinate line, we see that these solutions belong to the interval [3; 6], which in turn is the intersection of the intervals [3; +∞) and (-∞; 6].
on the coordinate line, we see that these solutions belong to the interval [3; 6], which in turn is the intersection of the intervals [3; +∞) and (-∞; 6].
[3; +∞) ∩ (−∞; 6] = [3; 6]

Therefore, our answer was that the values of the variable x belong to the numerical interval [3; 6], that is, to the intersection of the sets of solutions of the first and second inequalities
x ∈ [3; 6]
Example 2. Solve the inequality 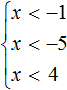
All inequalities included in the system have already been solved. We only need to specify the solutions that are common to all inequalities.
The solution of the first inequality is the numerical interval (-∞; -1).
The solution of the second inequality is the numeric interval (-∞; -5).
The solution of the third inequality is the numeric interval (-∞; 4).
The solution of the system 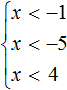 is the intersection of the numerical intervals (-∞; -1), (-∞; -5) and (-∞; 4). In this case this intersection is the interval (-∞; -5).
is the intersection of the numerical intervals (-∞; -1), (-∞; -5) and (-∞; 4). In this case this intersection is the interval (-∞; -5).
(−∞; −1) ∩ (−∞; −5) ∩ (−∞; 4) = (−∞; −5)
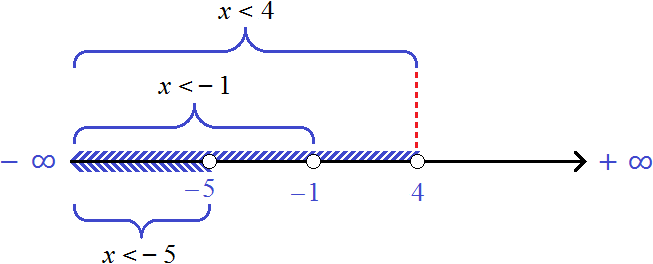
The picture shows numerical intervals and the inequalities with which these numerical intervals are given. It can be seen that the numbers belonging to the interval (-∞; -5) simultaneously belong to all the original intervals.
Let's write down the answer to system 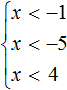 using the numeric interval:
using the numeric interval:
x ∈ (−∞; −5)
Example 3. Solve the inequality 
The solution of the first inequality y > 7 is the numerical interval (7; +∞).
The solution of the second inequality y < 4 is the numerical interval (-∞; 4).
The solution of the system  is the intersection of the numerical intervals (7; +∞) and (-∞; 4).
is the intersection of the numerical intervals (7; +∞) and (-∞; 4).
In this case, the intersection of the numerical intervals (7; +∞) and (-∞; 4) is an empty set, because these numerical intervals have no common elements:
(7; +∞) ∩ (−∞; 4) = ∅
If you draw the numerical intervals (7; +∞) and (-∞; 4) on the coordinate line, you will see that they do not intersect anywhere:

Union of sets
A union of two (or more) original sets is a set that consists of elements that belong to at least one of the original sets.
In practice, a union of sets consists of all elements belonging to the original sets. Therefore, the elements of such a set are said to belong to at least one of the original sets.
Consider the set A with elements 1, 2, 3 and the set B with elements 4, 5, 6.
A = { 1, 2, 3 }
B = { 4, 5, 6 }
Define a new set C and add to it all elements of the set A and all elements of the set B
C = { 1, 2, 3, 4, 5, 6 }
In this case, the union of sets A and B is set C and is denoted as follows:
A ∪ B = C
The symbol ∪ means union and replaces - OR. Then the expression A ∪ B = C can be read as follows:
Elements that belong to set A OR to set B are elements that belong to set C.
The definition of union says that the elements of such a set belong to at least one of the original sets. This phrase can be understood in the literal sense.
Let us return to the set C, which includes all the elements of sets A and B. Let's take element 5 from this set as an example. What can we say about it?
If 5 is an element of set C, and set C is the union of sets A and B, then we can surely say that element 5 belongs to at least one of the sets A and B. This is the case:
A = { 1, 2, 3 }
B = { 4, 5, 6 }
C = { 1, 2, 3, 4, 5, 6 }
Take another element from the set C, for example, element 2. What can we say about it?
If 2 is an element of set C, and set C is the union of sets A and B, then we can confidently state that element 2 belongs to at least one of the sets A and B. This is the case:
A = {1, 2, 3}
B = {4, 5, 6}
C = { 1, 2, 3, 4, 5, 6 }
If we want to union of two or more sets and suddenly find that one or more elements belong to each of these sets, then the repeated elements will enter the union only once.
For example, consider set A with elements 1, 2, 3, 4 and set B with elements 2, 4, 5, 6.
A = {1, 2, 3, 4}
B = {2, 4, 5, 6}
We see that elements 2 and 4 belong to both sets A and B at the same time. If we want to union sets A and B, then the new set C will contain elements 2 and 4 only once. This is what it looks like:
C = { 1, 2, 3, 4, 5, 6 }
To avoid mistakes when uniting, the usual way is to first add all elements of the first set to the new set, then add the elements of the second set that do not belong to the first set. Let us try to do such a union with sets A and B.
So we have the following original sets:
A = { 1, 2, 3, 4 }
B = { 2, 4, 5, 6 }
Define a new set C and add to it all the elements of the set A
C = { 1, 2, 3, 4,
Now add elements from the set B that do not belong to the set A. Elements 5 and 6 do not belong to the set A. We add them to the set C
C = { 1, 2, 3, 4, 5, 6 }
Example 2. John's friends are Tom, Fred, Max, and George. And Michael's friends are Leo, Tom, Fred and Evan. Find the union of the sets of John's and Michael's friends.
To begin with we define two sets: the set of John's friends and the set of Michael's friends.
Friends of John = { Tom,
Fred,
Max,
George }
Michael's friends = { Leo,
Tom,
Fred,
Evan }
Set up a new set called "All of John and Michael's Friends" and add all of John and Michael's friends to it.
Note that Tom and Fred are both friends of John and Michael, so we will add them to the new set only once, since there are no two Toms and two Freds at once.
All of John and Michael's Friends = { Tom, Fred, Max, George, Leo, Evan }
John's Friends ∪ Michael's Friends = All of John and Michael's Friends
In this case, the set of all of John's and Michael's friends is the union of the sets of John's and Michael's friends.
Example 3. Given two numerical intervals: [-7; 0] and [-3; 5]. Find their union.
Both intervals have square brackets, so their boundaries belong to them.
For illustration, let us list all the integers that belong to these intervals:
−7, −6, −5, −4, −3,−2, −1, 0 ∈ [−7; 0]
−3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
The union of the numeric intervals [-7; 0] and [-3; 5] will be the numeric interval [-7; 5], which contains all the numbers of the interval [-7; 0] and [-3; 5] without repeating some of the numbers
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Note that the numbers -3,-2, -1 belonged to both the first interval and the second one. But since the union is allowed to include such elements only once, we included them once.
So the union of the numeric intervals [-7; 0] and [-3; 5] will be the numeric interval [-7; 5].
[−7; 0] ∪ [−3; 5] = [−7; 5]
On the coordinate line, draw the intervals [-7; 0] and [-3; 5]. On the upper area mark the numerical interval [-7; 0], on the lower area mark the interval [-3; 5].
![]()
Earlier we found out that the interval [-7; 5] is a union of the intervals [-7; 0] and [-3; 5]. Here it is useful to recall the definition of union of sets, which was given at the beginning. A union is interpreted as a set consisting of all elements belonging to at least one of the original sets.
Indeed, if we take any number from the interval [-7; 5], we will find that it belongs to at least one of the intervals: either [-7; 0] or [-3; 5].
Take any number from the interval [-7; 5], for example number 2. Since the interval [-7; 5] is a union of [-7; 0] and [-3; 5], the number 2 will belong to at least one of these intervals. In this case, the number 2 belongs to the interval [-3; 5]

Let's take another number. For example, the number -4. This number will belong to at least one of the intervals: [-7; 0] or [-3; 5]. In this case it belongs to the interval [-7; 0]
Let's take another number. For example, the number -2. It belongs to the interval [-7; 0] as well as to the interval [-3; 5]. But on the coordinate line it is shown only once, because there are no two numbers -2 at once in one point.
Not every union of numeric intervals is a numeric interval. For example, try to find the union of the numeric intervals [-2; -1] and [4; 7].
The idea is the same: the union of numeric intervals [-2; -1] and [4; 7] is a set consisting of elements belonging to at least one of the intervals: [-2; -1] or [4; 7]. But this set will not be a numeric interval. For illustration, let us list all the integers belonging to this union:
[−2; −1] ∪ [4; 7] = { −2, −1, 4, 5, 6, 7 }
We obtained the set { -2, -1, 4, 5, 6, 7 }. This set is not a numeric interval, because the numbers between -1 and 4 are not included in the resulting set
![]()
The numeric interval must contain all numbers from the left border to the right. If one of the numbers is missing, the numerical space is meaningless. Suppose there is a ruler 15 cm long

This ruler is a numerical interval [0; 15], because it contains all numbers in the interval from 0 to 15 inclusive. Now imagine that on the ruler the number 9 is followed immediately by the number 12.

This ruler is not a 15 cm ruler, and it is undesirable to use it to measure. Also, it cannot be called a numerical interval [0; 15] because it does not contain all the numbers it should have contained.
Solving inequalities containing the sign ≠
Some inequalities contain the sign ≠ (not equal). For example, 2x ≠ 8. To solve such an inequality, you need to find the set of values of the variable x, in which the left part is not equal to the right part.
Solve the inequality 2x ≠ 8. Divide both parts of this inequality by 2, then we obtain:
We obtain an equal inequality x ≠ 4. The solution of this inequality is the set of all numbers not equal to 4. That is, if we substitute into the inequality x ≠ 4 any number that is not equal to 4, we obtain the correct inequality.
For example, let's substitute the number 5
5 ≠ 4 is a valid inequality because 5 is not equal to 4
Let's substitute the number 7
7 ≠ 4 - correct inequality because 7 is not equal to 4
And since the inequality x ≠ 4 is equivalent to the original inequality 2x ≠ 8, the solutions of the inequality x ≠ 4 will also fit the inequality 2x ≠ 8. Let us substitute the same test values 5 and 7 into the inequality 2x ≠ 8.
2 × 5 ≠ 8
2 × 7 ≠ 8
Let us represent the set of solutions to the inequality x ≠ 4 on the coordinate line. To do this, we mark the point 4 on the coordinate line, and mark the rest of the area on both sides with strokes:

Now let's write the answer in the form of a numeric interval. To do this we use the union of sets. Any number that is a solution of the inequality 2x ≠ 8 will belong either to the interval (-∞; 4) or to the interval (4; +∞). Thus we write that the values of the variable x belong to (-∞; 4) or (4; +∞). Recall that for the word "or" the symbol ∪
x ∈ (−∞; 4) ∪ (4; +∞)
This expression says that the values taken by the variable x belong to the interval (-∞; 4) or to the interval (4; +∞).
Inequalities containing the sign ≠ can also be solved like ordinary equations. To do this, replace the sign of ≠ with the sign =. Then you get an ordinary equation. At the end of the solution the found value of the variable x must be excluded from the set of solutions.
Solve the previous inequality 2x ≠ 8 as an ordinary equation. Replace the sign of ≠ with the equal sign =, we obtain the equation 2x = 8. Divide both parts of this equation by 2, we obtain x = 4.
We see that when x equals 4, the equation turns into a correct numerical equality. At other values the equation will not hold. We are interested in these other values. To do this we just need to exclude the found four from the set of solutions.
Example 2. Solve the inequality 3x - 5 ≠ 1 - 2x
Move -2x from the right side to the left side, changing the sign, and move -5 from the left side to the right side, again changing the sign:
![]()
Let us give like terms in both parts:
![]()
Divide both parts of the resulting inequality by 5
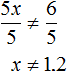
The solution of the inequality x ≠ 1.2 is the set of all numbers not equal to 1.2
Draw the set of solutions to the inequality x ≠ 1.2 on the coordinate line and write the answer as a numeric interval:
x ∈ (−∞; 1.2) ∪ (1.2; +∞)
This expression says that the values taken by the variable x belong to the interval (-∞; 1.2) or to the interval (1.2; +∞)
Solving sets of inequalities
Consider another type of inequalities called set inequalities. This type of inequalities may be rare to solve, but for general development it is useful to study them as well.
A set of inequalities is very similar to a system of inequalities. The difference is that in a system of inequalities you need to find a set of solutions satisfying each inequality that forms the system.
And in the case of a set of inequalities, you need to find the set of solutions satisfying at least one inequality that forms this set.
A set of inequalities is denoted by a square bracket. For example, the following entry of two inequalities is a set:
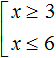
Let's solve this set. We first need to solve each inequality separately.
The solution of the first inequality x ≥ 3 is the numeric interval [3; +∞). The solution of the second inequality x ≤ 6 is the numerical interval (-∞; 6].
The set of values of x for which at least one of the inequalities is true will belong to the interval [3; +∞) or to the interval (-∞; 6]. We write it this way:
x ∈ [3; +∞) ∪ (-∞; 6]
This expression says that the variable x included in the set 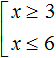 takes all values belonging to the interval [3; +∞) or the interval (-∞; 6]. This is what we need. To solve a set means to find a set of solutions satisfying at least one inequality of this set. Any number from interval [3; +∞) or interval (-∞; 6] will satisfy at least one inequality.
takes all values belonging to the interval [3; +∞) or the interval (-∞; 6]. This is what we need. To solve a set means to find a set of solutions satisfying at least one inequality of this set. Any number from interval [3; +∞) or interval (-∞; 6] will satisfy at least one inequality.
For example, the number 9 from the interval [3; +∞) satisfies the first inequality x ≥ 3. The number -7 from the interval (-∞; 6] satisfies the second inequality x ≤ 6.
Look carefully at the expression x ∈ [3; +∞) ∪ (-∞; 6], namely its right-hand side. Indeed, the expression [3; +∞) ∪ (-∞; 6] is a union of the numerical intervals [3; +∞) and (-∞; 6]. More precisely, the union of the sets of solutions of the first and second inequalities.
Thus, the solution of the set of inequalities is the union of the sets of solutions of the first and second inequalities.
In other words, the solution of set 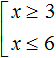 is the union of the numerical intervals [3; +∞) and (-∞; 6].
is the union of the numerical intervals [3; +∞) and (-∞; 6].

The union of numerical spaces [3; +∞) and (-∞; 6] is the space (-∞; +∞). More precisely, the union of the numerical intervals [3; +∞) and (-∞; 6] is the whole coordinate line. And the whole coordinate line is all the numbers which can only be
[3; +∞) ∪ (−∞; 6] = (−∞; +∞)
You can leave the answer as we wrote it down earlier:
x ∈ [3; +∞) ∪ (−∞; 6]
or replace it with a shorter one:
x ∈ (−∞; +∞)
Take any number from the resulting union, and check if it satisfies at least one inequality.
Take for example number 8. It satisfies the first inequality x ≥ 3.
8 ≥ 3
Take some other number, such as number 1. It satisfies the second inequality x ≤ 6
1 ≤ 6
Take some other number, for example number 5. It satisfies both the first inequality x ≥ 3 and the second inequality x ≤ 6

Example 2. Solve the set of inequalities 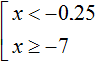
To solve this set, we need to find the set of solutions that satisfy at least one inequality that forms this set.
First, find the set of solutions to the first inequality x < -0.25. This set is the numerical interval (-∞; -0.25).
The set of solutions of the second inequality x ≥ -7 is the numerical interval [-7; +∞).
The solution of the set of inequalities 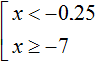 will be the union of the sets of solutions of the first and second inequalities.
will be the union of the sets of solutions of the first and second inequalities.
x ∈ (−∞; −0.25) ∪ [−7; +∞)
In other words, the solution to the set 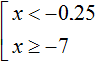 is the union of the sets of solutions of the first and second inequalities.
is the union of the sets of solutions of the first and second inequalities.

The union of numerical intervals (-∞; -0.25) and [-7; +∞) is the whole coordinate line. And the whole coordinate line is all the numbers which can only be
(−∞; −0.25) ∪ [−7; +∞) = (−∞; +∞)
You can leave the answer as we wrote it down earlier:
x ∈ (−∞; −0.25) ∪ [−7; +∞)
or replace it with a shorter one:
x ∈ (−∞; +∞)
Example 3. Solve the set of inequalities 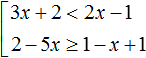
Let's solve each inequality separately:
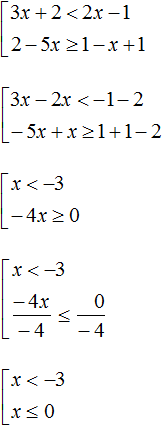
The set of solutions of the first inequality x < -3 is the numerical interval (-∞; -3).
The set of solutions of the second inequality x ≤ 0 is the numerical interval (-∞; 0].
The solution of the set of inequalities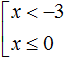 is the union of the sets of solutions of the first and second inequalities.
is the union of the sets of solutions of the first and second inequalities.
x ∈ (−∞; −3) ∪ (−∞; 0]
In other words, the solution of set 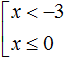 is the union of the numerical intervals (-∞; -3) and (-∞; 0].
is the union of the numerical intervals (-∞; -3) and (-∞; 0].

The union of the numerical intervals (-∞; -3) and (-∞; 0] is the numerical interval (-∞; 0]
(−∞; −3) ∪ (−∞; 0] = (−∞; 0]
You can leave the answer as we wrote it down earlier:
x ∈ (−∞; −3) ∪ (−∞; 0]
or replace it with a shorter one:
x ∈ (−∞; 0]
Tasks for independent decision
B = { 3, 4, 5 }
A ∪ B = { 1, 2, 3, 4, 5 }
A = { -3, -2, -1, 0, 1, 2 }
B = { 1, 2, 3, 4, 5 }
A ∪ B = { −3, −2, −1, 0, 1, 2, 3, 4, 5 }
B = { 3, 4 }
A ∪ B = { 1, 2, 3, 4 }
[−2; 7) ∩ (0; 10] = (0; 7)
[−2; 7) ∪ (0; 10] = [−2; 10]
(−∞; 3] ∩ [−2; 1) = [−2; 1)
(−∞; 3] ∪ [−2; 1) = (−∞; 3]

(3; +∞) ∩ [2; +∞) = (3; +∞)
(3; +∞) ∪ [2; +∞) = [2; +∞)
[−3; −1] ∩ (−2; 4] = (−2; −1]
[−3; −1] ∪ (−2; 4] = [−3; 4]

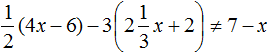
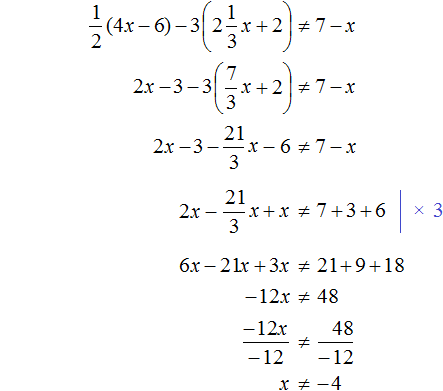

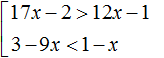
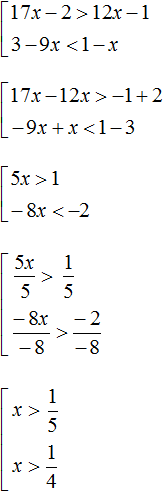

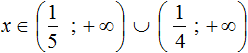

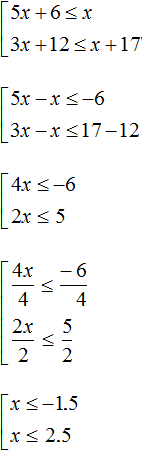

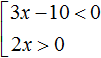
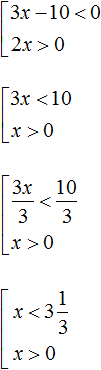

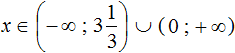
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.