Expanding a binomial
A binomial is a polynomial consisting of two terms. In the previous lessons, we raised a polynomial to the second and third powers, thus obtaining the formulas for reduced multiplication:
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
But a binomial can be raised not only to the second and third powers, but also to the fourth, fifth, or higher powers.
For example, take binomial a + b to the fourth power:
(a + b)4
Let us represent this expression as the product of a + b and the cube of the same binomial
(a + b)(a + b)3
The factor (a + b)3 can be replaced by the right-hand side of the formula for the cube of the sum of the two expressions. Then we obtain:
(a + b)(a3 + 3a2b + 3ab2 + b3)
This is the usual multiplication of polynomials. Let's perform it:
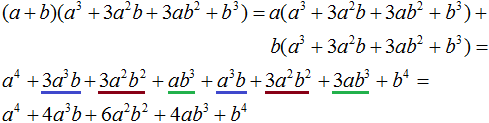
That is, if you raise a + b to the fourth power you get a polynomial a4 + 4a3b + 6a2b2 + 4ab3 + b4
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
The raising of a + b to the fourth power can also be done as follows: represent the expression (a + b)4 as the product of powers of (a + b)2(a + b)2
(a + b)2(a + b)2
But the expression (a + b)2 equals a2 + 2ab + b2. Replace in the expression (a + b)2(a + b)2 the squares of the sum by the polynomial a2 + 2ab + b2
(a2 + 2ab + b2)(a2 + 2ab + b2)
This is again the usual multiplication of polynomials. Let's perform it. We get the same result as before:
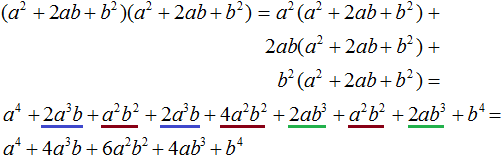
Expanding a trinomial
A trinomial is a polynomial consisting of three terms. For example, the expression a + b + c is a trinomial.
Sometimes you may have the task of raising a trinomial to a power. For example, square the trinomial a + b + c
(a + b + c)2
Two terms inside the brackets can be bracketed. For example, put the sum of a + b in brackets:
((a + b) + c)2
In this case the sum of a + b will be treated as one term. Then it turns out that we are not squaring a trinomial, but a binomial. The sum of a + b will be the first term, and the term c will be the second term. And we already know how to square a binomial. To do this, we can use the formula for squaring the sum of two expressions:
(a + b)2 = a2 + 2ab + b2
Let's apply this formula to our example:
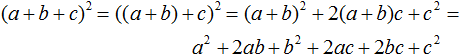
In the same way, a polynomial with four or more terms can be squared. For example, squared the polynomial a + b + c + d
(a + b + c + d)2
Let us represent the polynomial as a sum of two expressions: a + b and c + d. To do this, put them in brackets:
((a + b) + (c + d))2
Now use the formula for the square of the sum of two expressions:
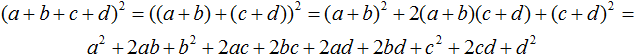
Extraction of a complete square from a quadratic trinomia
Another identical transformation that may be useful in solving tasks is the extraction of the full square from a quadratic trinomial.
A quadratic trinomial is a trinomial of the second power. For example, the following trinomials are quadratic:
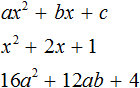
The idea of extracting a full square from such trinomials is to represent the original square trinomial as an expression (a + b)2 + c, where (a + b)2 is a full square and c is some numeric or alphabetic expression.
For example, let's extract the complete square of the trinomial4x2 + 16x + 19.
First we need to construct an expression of the form a2 + 2ab + b2. We will construct it from the trinomial 4x2 + 16x + 19. First, let's determine which terms will be denoted by variables a and b
The variable a will be the term 2x because the first term of the trinomial 4x2 + 16x + 19, namely 4x2 is obtained if 2x is squared:
(2x)2 = 4x2
So the variable a is 2x
a = 2x
Now we return to the original trinomial and immediately pay attention to the expression 16x. This expression is the doubled product of the first expression a (in our case it is 2x) and the second expression b, which we don't know yet. We temporarily put a question mark in its place:
2 × 2x × ? = 16x
If we look carefully at the expression 2 × 2x × ? = 16x, then intuitively it becomes clear that the term b in this situation is number 4, because the expression 2 × 2x equals 4x, and to get 16x you need to multiply 4x by 4.
2 × 2x × 4 = 16x
From this we conclude that the variable b is 4
b = 4
So our complete square would be the expression (2x)2 + 2 × 2x × 4 + 42
Now we are all set to extract the complete square from the trinomial 4x2 + 16x + 19.
So, let's return to the original trinomial 4x2 + 16x + 19 and try to carefully embed the full square (2x)2 + 2 × 2x × 4 + 42
4x2 + 16x + 19 =
Instead of 4x2 write (2x)2
4x2 + 16x + 19 = (2x)2
Then instead of 16x we write the doubled product, which is 2 × 2x × 4
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4
Then we add the square of the second expression:
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42
And term 19 for the time being, we'll rewrite it as it is:
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 + 19
Now note that the polynomial (2x)2 + 2 × 2x × 4 + 42 + 19 is not identical to the original trinomial 4x2 + 16x + 19. Verify this by converting the polynomial (2x)2 + 2 × 2x × 4 + 42 + 19 to the standard form:
(2x)2 + 2 × 2x × 4 + 42 + 19 = 4x2 + 16x + 42 + 19
We see that we get a polynomial 4x2 + 16x + 42 + 19, and we should have gotten 4x2 + 16x + 19. This is because the term 42 was artificially introduced into the original trinomial in order to arrange a complete square of the trinomial 4x2 + 16x + 19.
To save the value of the original polynomial, after adding the term 42 you must immediately subtract it
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19
Now the expression (2x)2 + 2 × 2x × 4 + 42 can be written as (a + b)2. In our case we obtain the expression (2x + 4)2
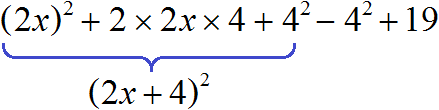
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19 = (2x + 4)2 − 42 + 19
The remaining terms -42 and 19 can be added together. -42 is -16, hence -16 + 19 = 3
4x2 + 16x + 19 = (2x)2 + 2 × 2x × 4 + 42 − 42 + 19 = (2x + 4)2 − 42 + 19 = (2x + 4)2 + 3
So, 4x2 + 16x + 19 = (2x + 4)2 + 3
Example 2. Extract the full square from the quadratic trinomial x2 + 2x + 2
First, we construct an expression of the form a2 +2ab + b2. The variable a in this case is x, since x2 = x2.
We rewrite the next term of the original trinomial 2x as the doubled product of the first expression (this is x) and the second expression b (this is 1).
2 × x × 1 = 2x
If b = 1, then the complete square is x2 + 2x + 12.
Now let's go back to the original quadratic trinomial and introduce the full square x2 + 2x + 12 into it
x2 + 2x + 2 = x2 + 2x + 12 − 12 + 2 = (x + 1)2 + 1
As in the previous example, the term b (in this example it is 1) was immediately subtracted after addition in order to preserve the value of the original trinomial.
Consider the following numerical expression:
9 + 6 + 2
The value of this expression is 17
9 + 6 + 2 = 17
Let's try to isolate the complete square in this numerical expression. To do this, we first construct an expression of the form a2 + 2ab + b2. The variable a in this case is number 3, because the first term of the expression 9 + 6 + 2, namely 9, can be represented as 32.
The second term 6 is presented as the doubled product of the first term 3 and the second term 1
2 × 3 × 1 = 6
That is, the variable b will be equal to one. Then the complete square is the expression 32 + 2 × 3 × 1 + 12. Introduce it into the original expression:
32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2
Let's make a complete square, and add the terms -12 and 2:
32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2 = (3 + 1)2 + 1
You get the expression (3 + 1)2 + 1, which is still 17
(3 + 1)2+1 = 42 + 1 = 17
Suppose we have a square and two rectangles. A square with side 3 cm, a rectangle with sides 2 cm and 3 cm, and a rectangle with sides 1 cm and 2 cm
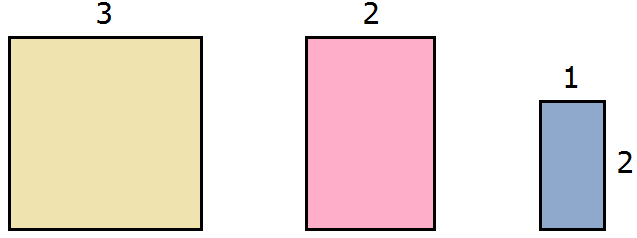
Let's calculate the area of each figure. The area of the square is 32 = 9 cm2, the area of the pink rectangle is 2 × 3 = 6 cm2, the area of the lilac rectangle is 1 × 2 = 2 cm2.
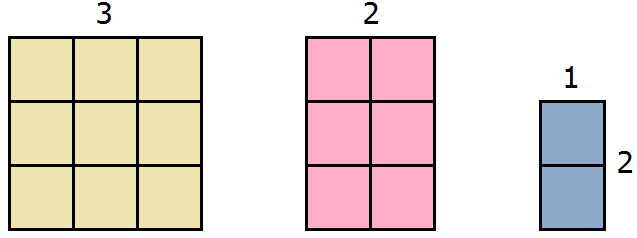
Write down the sum of the areas of these rectangles:
9 + 6 + 2
This expression can be understood as the union of a square and two rectangles into a single figure:

Then we obtain a figure with an area of 17 cm2. Indeed, the given figure contains 17 squares with a side of 1 cm.
Let's try to form a square from the existing figure. And as big a square as possible. To do this we will use parts of the pink and lilac rectangle.
To form a larger square of the existing shape, you can leave the yellow square unchanged, and half of the pink rectangle attached to the bottom of the yellow square:
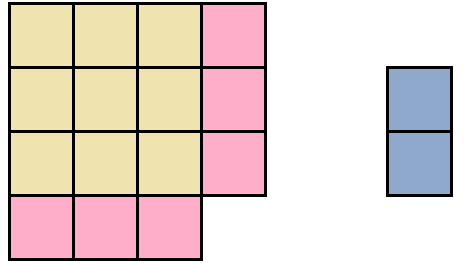
We see that one more square centimeter is missing to form a complete square. We can take it from the lilac rectangle. So, take one square from the lilac rectangle and attach it to form a large square:
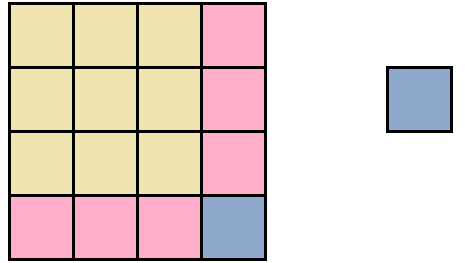
Now look carefully at what we have obtained. Namely on the yellow part of the figure and the pink part, which essentially enlarged the former yellow square. Doesn't this mean that there was a side of the square equal to 3 cm, and this side was enlarged by 1 cm, resulting in an increase in area?
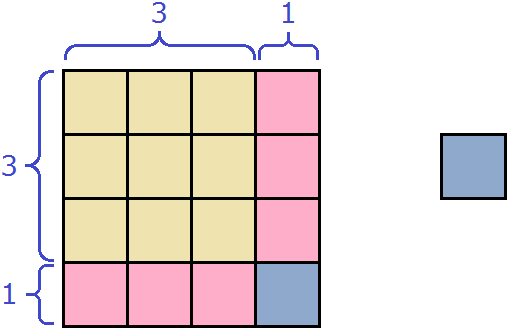
(3 + 1)2
The expression (3 + 1)2 is 16 because 3 + 1 = 4 and 42 = 16. The same result can be obtained by using the formula for the square of the sum of two expressions:
(3 + 1)2 = 32 + 6 + 1 = 9 + 6 + 1 = 16
Indeed, the resulting square contains 16 squares.
The remaining one square from the lilac rectangle can be attached to the resulting large square. After all, originally we were talking about a single figure:
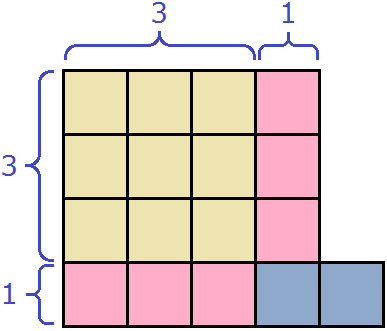
(3 + 1)2 + 1
Attaching a small square to an existing large square is described by the expression (3 + 1)2 + 1. And this is the extraction of the full square from the expression 9 + 6 + 2
9 + 6 + 2 = 32 + 6 + 2 = 32 + 2 × 3 × 1 + 12 − 12 + 2 = (3 + 1)2 + 1
The expression (3 + 1)2 + 1, as well as the expression 9 + 6 + 2 is 17. Indeed, the area of the formed figure is 17 cm2.
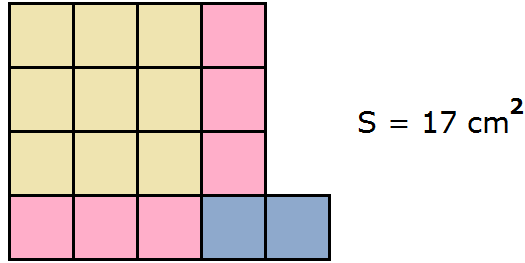
Example 4. Execute the extraction of the full square from the quadratic trinomial x2 + 6x + 8
x2 + 6x + 8 = x2 + 2 × x × 3 + 32 − 32 + 8 = (x + 3)2 − 1
In some examples, when constructing the expression a2 + 2ab + b2, it is not possible to immediately determine the values of the variables a and b.
For example, extract the full square from the quadratic trinomial x2 + 3x + 2
The variable a corresponds to x. The second term 3x cannot be represented as a doubled product of the first expression and the second. In this case the second term should be multiplied by 2, and to keep the value of the original polynomial unchanged, immediately divide by 2. This will look like this:
![]()
The resulting fraction is ![]() and contains the values of variables a and b. Our task is to be able to recognize them correctly. Rewrite this fraction as the product of multiplier 2, fraction
and contains the values of variables a and b. Our task is to be able to recognize them correctly. Rewrite this fraction as the product of multiplier 2, fraction ![]() , and the variable x
, and the variable x
![]()
Now the second term is represented as the doubled product of the first expression and the second. The variable a, as stated earlier, is equal to x. And the variable b is equal to the fraction ![]()
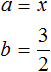
Go back to our example and add the square of the second expression, and so that the value of the expression does not change, immediately subtract it:
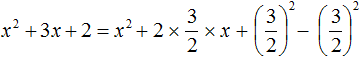
Add the remaining term 2
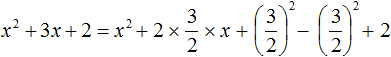
Let's make a full square:
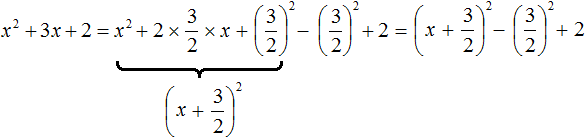
The remaining square of the second expression and the number 2 can be added. We end up with:
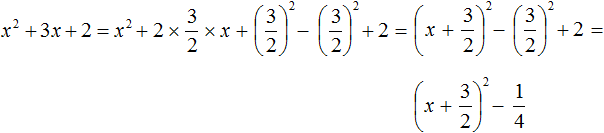
Example 6. Select the full square from the quadratic trinomial 9x2 + 18x + 7
![]()
Example 7. Select the full square from the quadratic trinomial x2 − 10x + 1
In this trinomial, the first two terms are connected by a minus sign. In this case, as before, we need to extract the complete square, but it will be the square of the difference. Simply put, we need to construct an expression of the form a2 − 2ab + b2.
![]()
Example 8. Select the full square from the quadratic trinomial 16x2 + 4x + 1
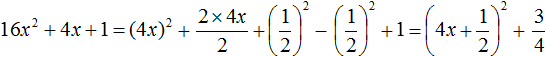
Example 9. Decompose the polynomial x2 + 6x + 8 into multipliers using the allocation of the full square.
Let's first select a complete square:
![]()
The resulting polynomial (x + 3)2 − 1 is the difference of squares, since the unit can be represented as 12. Use the formula for difference of squares and decompose the polynomial (x + 3)2 − 1 into multiples:
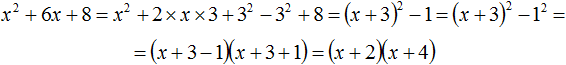
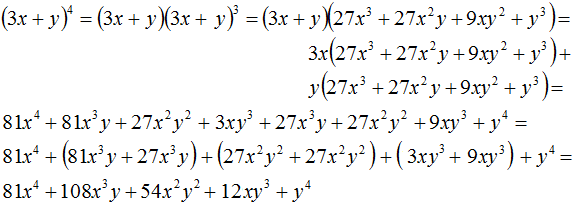
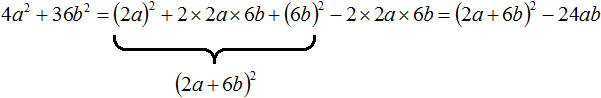
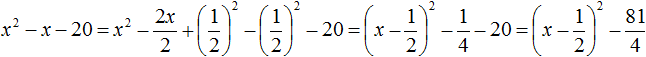
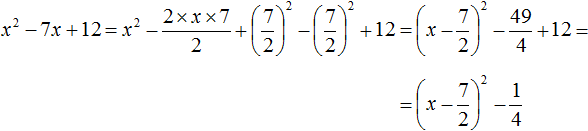
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.