Converting mixed repeating decimals to fractions

To convert a mixed repeating decimals to fractions, write in the numerator the difference where the minuend is the digits standing after the point in the fraction and the subtrahend are the digits standing between the point and the first period of the fractions.

For example, convert the mixed repeating decimal 0.31 (6) to fraction.

First, write the difference in the numerator. All digits after the decimal point (including the period) will be the decomposer, and the digits between the decimal point and the period will be the subtraction:

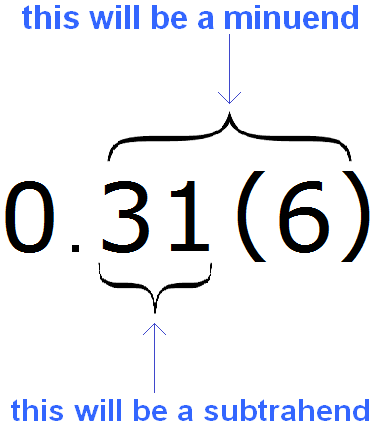
So we write the difference in the numerator:

And in the denominator we write some number of nines and zeros. The number of nines must be equal to the number of digits in the period of the periodic fraction 0.31 (6)

In the decimal 0.31 (6), the period consists of one digit. So we write one nine in the denominator of the fraction:

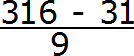
Now add the number of zeros. The number of zeros must be equal to the number of digits between the decimal point and the period of the periodic fraction.

In the fraction 0.31 (6) there are two digits between the decimal point and the period. So there must be two zeros in the denominator of the fraction. Add them:

We got an expression that is easy to calculate:

We got the answer

Thus, when you convert the periodic fraction 0.31 (6) to fraction, you get

Example 2. Convert the mixed repeating decimal 0.72 (62) into a to fraction

First, write the difference in the numerator. All digits after the decimal point (including the period) minus  the digits between the decimal point and the period:

So we write the difference in the numerator:

And in the denominator we write some number of nines and zeros. The number of nines must be equal to the number of digits in the period of the repeating decimal 0.72 (62)

In 0.72 (62) decimal the period consists of two digits. So we write two nines in the denominator of the fraction:

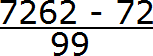
Now add the number of zeros. The number of zeros must be equal to the number of digits between the decimal point and the period of the repeating decimal .

In the fraction 0.72 (62) there are two digits between the decimal point and the period. So there must be two zeros in the denominator of the fraction. Add them:

We got an expression that is easy to calculate:

The answer is 

So when you convert the periodic fraction 0.72 (62) into an ordinary fraction, you get

Video lesson

Add comment