We continue to study polynomials. In this lesson we will learn how to multiply polynomials using the reduced multiplication formulas.
The square of the sum of two expressions
There are a number of cases where the multiplication of a polynomial by a polynomial can be greatly simplified. This is, for example, the case of (2x + 3y)2.
The expression (2x + 3y)2 is a multiplication of two polynomials, each of which is equal to (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
We obtained the multiplication of a polynomial by a polynomial. Let's perform it:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2
That is, the expression (2x + 3y)2 is 4x2 + 12xy + 9y2
(2x + 3y)2 = 4x2 + 12xy + 9y2
Let's solve a similar example, which is simpler:
(a + b)2
The expression (a + b)2 is a multiplication of two polynomials, each equal to (a + b)
(a + b)2 = (a + b)(a + b)
Let's perform this multiplication:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
That is, the expression (a + b)2 is a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
It turns out that the case (a + b)2 can be extended for any a and b. The first example we solved, namely (2x + 3y)2, can be solved using the identity (a + b)2 = a2 + 2ab + b2. To do this, substitute the terms from (2x + 3y)2 instead of the variables a and b. In this case the a variable corresponds to the term 2x, and the b variable corresponds to the term 3y
a = 2x
b = 3y
And then you can use the identity (a + b)2 = a2 + 2ab + b2, but instead of variables a and b you must substitute the expressions 2x and 3y, respectively:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2
As in the last time we obtained the polynomial 4x2 + 12xy + 9y2. The solution is usually written in a shorter form, performing all elementary transformations in mind:
(2x + 3y)2 = 4x2 + 12xy + 9y2
The identity (a + b)2 = a2 + 2ab + b2 is called the formula for the square of the sum of two expressions. This formula can be read as follows:
The square of the sum of two expressions is equal to the square of the first expression plus twice the product of the first expression by the second expression plus the square of the second expression.
Consider the expression (2 + 3)2. It can be calculated in two ways: add in parentheses and square the result, or use the formula for squaring the sum of two expressions.
First way:
(2 + 3)2 = 52 = 25
Second way:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Example 2. Convert the expression (5a + 3)2 into a polynomial.
Use the formula for the square of the sum of two expressions:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
So (5a + 3)2 = 25a2 + 30a + 9.
Let's try to solve this example without using the sum squared formula. We should get the same result:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
The formula for the square of the sum of two expressions has a geometric meaning. We remember that in order to calculate the area of a square you have to raise its side to the second power.
For example, the area of a square with side a will be a2. If we increase the side of the square by b, the area will be equal to (a + b)2
Consider the following figure:

Imagine that the side of the square shown in this picture is increased by b. All sides of the square are equal. If its side is increased by b, then the other sides are also increased by b
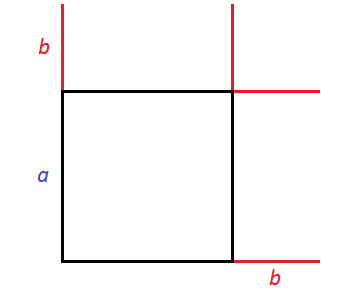
We got a new square, which is larger than the previous one. To see it well, add the missing sides:
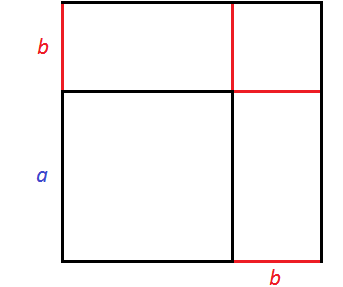
To calculate the area of this square, you can separately calculate the squares and rectangles included in it, then add up the results.
First, you can calculate a square with side a - its area will be equal to a2. Then you can calculate rectangles with sides a and b - they will be equal to ab. Then you can calculate a square with side b
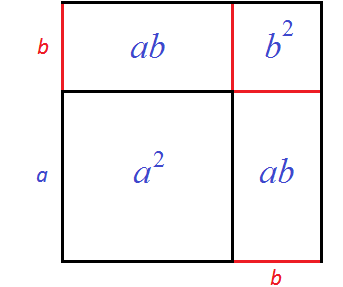
The result is the following sum of areas:
a2 + ab + ab + b2
The sum of areas of identical rectangles can be replaced by the multiplication of 2ab, which literally means "to repeat twice the area of rectangle ab". Algebraically, this is obtained by reducing like terms ab and ab. The result is the expression a2 + 2ab + b2, which is the right-hand side of the formula for the square of the sum of two expressions:
(a + b)2 = a2 + 2ab + b2
The square of the difference of two expressions
The formula for the square of the difference of two expressions is as follows:
(a − b)2 = a2 − 2ab + b2
This formula can be read as follows:
The square of the difference of two expressions is equal to the square of the first expression minus twice the product of the first expression by the second plus the square of the second expression.
The formula for the square of the difference of two expressions is derived in the same way as the formula for the square of the sum of two expressions. The expression (a - b)2 is the product of two polynomials, each equal to (a - b)
(a − b)2 = (a − b)(a − b)
If you perform this multiplication, you will get polynomial a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Example 1. Convert the expression (7x - 5)2 into a polynomial.
Use the formula for the square of the difference of two expressions:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
So (7x − 5)2 = 49x2 − 70x + 25.
Let's try to solve this example without using the squared difference formula. We should get the same result:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
The formula for the square of the difference of two expressions also has a geometric meaning. If the area of a square with side a is a2, then the area of the square whose side is reduced by b will be (a - b)2
Consider the following figure:

Imagine that the side of the square shown in this picture was reduced by b. All sides of the square are equal. If one side is reduced by b, then the other sides are also reduced by b
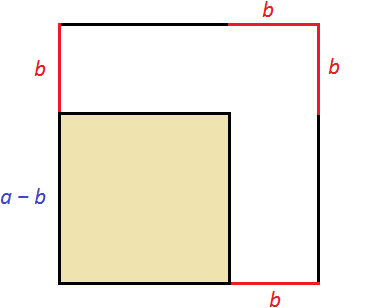
We got a new square, which is smaller than the previous one. It is highlighted in yellow in the picture. Its side is equal to a - b, because the old side a has been reduced by b. To calculate the area of this square, we can subtract from the original square's area a2 the areas of the rectangles that were obtained during the reduction of the sides of the old square. Let us show these rectangles:
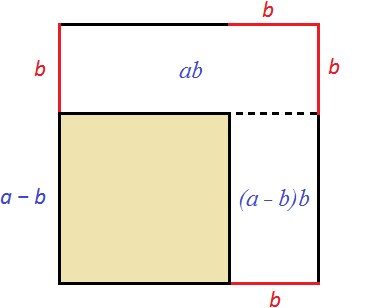
Then we can write the following expression: old area a2 minus area ab minus area (a - b)b
a2 − ab − (a − b)b
Open the brackets in the expression (a - b)b
a2 − ab − ab + b2
Let us give like terms:
a2 − 2ab + b2
The result is the expression a2 − 2ab + b2, which is the right part of the formula for the square of the difference of two expressions:
(a − b)2 = a2 − 2ab + b2
The formulas for the square of the sum and the square of the difference are generally called reduced multiplication formulas. These formulas allow you to greatly simplify and speed up the multiplication of polynomials.
Earlier we said that when considering a member of a polynomial separately, it should be considered together with the sign that is placed in front of it.
But when applying the reduced multiplication formulas, the sign of the original polynomial should not be regarded as the sign of the term itself.
For example, if an expression (5x - 2y)2 is given, and we want to use the formula (a − b)2 = a2 − 2ab + b2, then instead of b we should use 2y, not -2y. This is a peculiarity of working with formulas, which should not be forgotten.
(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2
If you substitute -2y, it will mean that the difference in parentheses of the original expression has been replaced by the sum:
(5x − 2y)2 = (5x + (−2y))2
and in that case you should not apply the formula for the square of the difference, but the formula for the square of the sum:
(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2
An exception may be expressions of the form (x - (-y))2. In this case, using the formula (a − b)2 = a2 − 2ab + b2 instead of b we should substitute (-y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
But when squaring expressions of the form x - (-y), it is more convenient to replace subtraction with addition of x + y. Then the original expression will look like (x + y)2 and you can use the formula for the sum squared instead of the difference:
(x + y)2 = x2 + 2xy + y2
The cube of the sum and the cube of the difference
The formulas for the cube of the sum of two expressions and the cube of the difference of two expressions are as follows:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
The formula for the cube of the sum of two expressions can be read as follows:
The cube of the sum of two expressions is equal to the cube of the first expression plus three times the product of the square of the first expression by the second expression plus three times the product of the first expression by the square of the second expression plus the cube of the second expression.
And the formula for the cube of the difference of two expressions can be read as follows:
The cube of the difference of two expressions is equal to the cube of the first expression minus three times the product of the square of the first expression by the second expression plus three times the product of the first expression by the square of the second expression minus the cube of the second expression.
When solving problems, it is desirable to know these formulas by heart. If you don't remember them, that's okay! You can derive them yourself. We already know how to do it.
Let's derive the formula for the cube of the sum by ourselves:
(a + b)3
The expression (a + b)3 is the product of three polynomials, each equal to (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
But the expression (a + b)3 can also be written as (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
In this case the factor (a + b)2 is the square of the sum of the two expressions. This sum square is equal to the expression a2 + 2ab + b2.
Then (a + b)3 can be written as (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
This is the multiplication of a polynomial by a polynomial. Let's perform it:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Similarly, we can derive the formula for the cube of the difference of two expressions:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Example 1. Convert the expression (x + 1)3 into a polynomial.
Use the formula for the cube of the sum of two expressions:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Let's try to solve this example without using the formula for the cube of the sum of two expressions. We will get the same result, but the solution will be longer:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Example 2. Convert the expression (6a2 + 3b3)3 into a polynomial.
Use the formula for the cube of the sum of two expressions:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3 = (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Example 3. Convert the expression (n2 − 3)3 into a polynomial.
Use the formula for the cube of the difference of two expressions:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Example 4. Convert the expression (2x2 − x3)3 into a polynomial.
Use the formula for the cube of the difference of two expressions:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9
Multiplying the difference of two expressions by their sum
There are tasks that require multiplying the difference of two expressions by their sum. For example:
(a − b)(a + b)
In this expression, the difference of two expressions a and b is multiplied by the sum of the same two expressions. Let us perform this multiplication:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
That is, the expression (a − b)(a + b) equals a2 − b2
(a − b)(a + b) = a2 − b2
We see that multiplying the difference of two expressions by their sum yields the difference of the squares of those expressions.
The product of the difference of two expressions and their sum is equal to the difference of the squares of these expressions.
The case of (a - b)(a + b) can be extended to any a and b. Simply put, if a task requires multiplying the difference of two expressions by their sum, then this multiplication can be replaced by the difference of the squares of these expressions.
Example 1. Perform multiplication of (2x - 5)(2x + 5)
In this example, the difference of expressions 2x and 5 is multiplied by the sum of the same expressions. Then according to the formula (a − b)(a + b) = a2 − b2 we have:
(2x − 5)(2x + 5) = (2x)2 − 52
Let's calculate the right part, we get 4x2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
Let's try to solve this example without using the formula (a − b)(a + b) = a2 − b2. We get the same result 4x2 − 25
(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25
Example 2. Multiply (4x - 5y)(4x + 5y)
Use the formula for multiplying the difference of two expressions by their sum:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2
Example 3. Multiply (2a + 3b)(2a - 3b)
Use the formula for multiplying the difference of two expressions by their sum:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
In this example, the sum of terms 2a and 3b was located earlier than the difference of these terms. In the formula (a - b)(a + b) = a2 − b2 the difference is earlier.
It makes no difference how the factors (a - b) in (a + b) are arranged in the formula. They can be written as (a - b)(a + b) or (a + b)(a - b). The result will still be a2 − b2, since the permutation of the factors does not change the product.
So in this example the factors (2a + 3b) and (2a - 3b) can be written as (2a + 3b)(2a - 3b) or (2a - 3b)(2a + 3b). The result will still be 4a2 − 9b2.
Example 4. Multiply (7 + 3x)(3x - 7)
Use the formula for multiplying the difference of two expressions by their sum:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49
Example 5. Perform multiplication of (x2 - y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Example 6. Multiply (-5x - 3y)(5x - 3y)
In the expression (-5x - 3y) we put -1 outside the brackets, then the original expression will take the following form:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Replace the product (5x + 3y)(5x - 3y) by the difference of squares:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
The difference of squares has been bracketed. If this is not done, it will turn out that -1 is multiplied only by (5x)2. And this will cause an error and change the value of the original expression.
Then we calculate the expression in brackets:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9x2)
Now multiply -1 by the expression in brackets and get the final result:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2
Multiplying the difference of two expressions by the incomplete square of their sum
There are tasks that require multiplying the difference of two expressions by the incomplete square of their sum. This expression looks like the following:
(a − b)(a2 + ab + b2)
The first polynomial (a - b) is the difference of two expressions, and the second polynomial (a2 + ab + b2) is the incomplete square of the sum of these two expressions.
The incomplete sum square is a polynomial of the form a2 + ab + b2. It is similar to the usual sum square a2 + 2ab + b2 except that the product of the first and second expressions is not doubled.
For example, the expression 4x2 + 6xy + 9y2 is the incomplete square of the sum of expressions 2x and 3y.
Indeed, the first term of the expression 4x2 + 6xy + 9y2, namely 4x2 is the square of the expression 2x, because (2x)2 = 4x2. The third term of the expression 4x2 + 6xy + 9y2, namely 9y2, is the square of the expression 3y, since (3y)2 = 9y2. The term in the middle of 6xy is the product of the expressions 2x and 3y.
So, multiply the difference (a - b) by the incomplete square of the sum a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
That is, the expression (a − b)(a2 + ab + b2) equals a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
This identity is called the formula for multiplying the difference of two expressions by the incomplete square of their sum. This formula can be read as follows:
The product of the difference of two expressions and the incomplete square of their sum equals the difference of the cubes of these expressions.
Example 1. Multiply (2x − 3y)(4x2 + 6xy + 9y2)
The first polynomial (2x - 3y) is the difference of two expressions 2x and 3y. The second polynomial 4x2 + 6xy + 9y2 is the incomplete square of the sum of the two expressions 2x and 3y. This allows you to use the formula (a − b)(a2 + ab + b2) = a3 − b3 without having to do long calculations. In our case, the multiplication (2x − 3y)(4x2 + 6xy + 9y2) can be replaced by the difference of the cubes 2x and 3y
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Let's try to solve the same example without using the formula (a − b)(a2 + ab + b2) = a3 − b3. We will get the same result, but the solution will be longer:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Example 2. Multiply (3 − x)(9 + 3x + x2)
The first polynomial (3 - x) is the difference of two expressions, and the second polynomial is the incomplete square of the sum of these two expressions. This allows us to use the formula (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Multiplying the sum of two expressions by the incomplete square of their difference
There are tasks that require multiplying the sum of two expressions by the incomplete square of their difference. This expression looks like the following:
(a + b)(a2 − ab + b2)
The first polynomial (a + b) is the sum of two expressions, and the second polynomial (a2 − ab + b2) is the incomplete square of the difference of these two expressions.
The incomplete difference square is a polynomial of the form a2 − 2ab + b2. It is similar to the usual difference square of a2 − 2ab + b2 except that the product of the first and second expressions is not doubled.
For example, the expression 4x2 − 6xy + 9y2 is the incomplete square of the difference of expressions 2x and 3y.
(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2
Let's return to the original example. Multiply the sum a + b by the incomplete square of the difference a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
That is, the expression (a + b)(a2 − ab + b2) equals a3 + b3
(a + b)(a2 − ab + b2) = a3 + b3
This identity is called the formula for multiplying the sum of two expressions by the incomplete square of their difference. This formula can be read as follows:
The product of the sum of two expressions and the incomplete square of their difference is equal to the sum of the cubes of these expressions.
Example 1. Multiply (2x + 3y)(4x2 − 6xy + 9y2)
The first polynomial (2x + 3y) is the sum of two expressions 2x and 3y, and the second polynomial 4x2 − 6xy + 9y2 is the incomplete square of the difference of these expressions. This allows us to use the formula (a + b)(a2 − ab + b2) = a3 + b3 without having to do long calculations. In our case, the multiplication (2x + 3y)(4x2 − 6xy + 9y2) can be replaced by the sum of the cubes 2x and 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Let's try to solve the same example without using the formula (a + b)(a2 − ab + b2) = a3 + b3. We will get the same result, but the solution will be longer:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Example 2. Multiply (2x + y)(4x2 − 2xy + y2)
The first polynomial (2x + y) is the sum of two expressions, and the second polynomial (4x2 − 2xy + y2) is the incomplete square of the difference of these expressions. This allows to use the formula (a + b)(a2 − ab + b2) = a3 + b3
(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3
Let's try to solve the same example without using the formula (a + b)(a2 − ab + b2) = a3 + b3. We will get the same result, but the solution will be longer:
(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) =
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.