Examples of solving systems of linear inequalities with one variable
Several linear inequalities satisfying the same solutions form a system.
Consider a simple example. System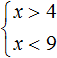 
consists of two inequalities that have already been solved.
Solutions of the first inequality are all numbers greater than 4. Solutions of the second inequality are all numbers that are less than 9.
Draw the set of solutions to each inequality on the coordinate line and write the answers to them as numerical intervals:
But the point is that the inequalities x > 4 and x < 9 are connected by a system sign, so they depend on each other. Our task is to specify solutions that simultaneously satisfy both the first and the second inequalities.
Simply put, you need to specify numbers that are greater than 4 but less than 9. Obviously, we are talking about numbers between 4 and 9.
So the solutions of the system 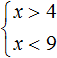are numbers from 4 to 9. Boundaries 4 and 9 are not included in the set of solutions of the system because the inequalities x > 4 and x < 9 are strict. The answer can be written as a numerical interval:
x ∈ ( 4 ; 9 )
Also, you need to represent the set of solutions of the system on the coordinate line.
For a system of linear inequalities, the solution on the coordinate line is shown as follows:
First, the boundaries of both inequalities are shown:
On the upper area mark the set of solutions of the first inequality x > 4
Mark the set of solutions of the second inequality x < 9 on the lower area
We are interested in the area that is marked with strokes on both sides. This is the area where the solutions of the system 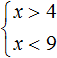are located. You can see that this area is located between 4 and 9. For clarity, we highlight this area in red:
To check, you can take any number from this interval and substitute it into the initial system 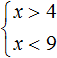. Take, for example, the number 6
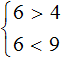
We see that solution 6 satisfies both inequalities. Take another number from the interval (4; 9), for example, the number 8
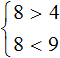
We see that solution 8 satisfies both inequalities.
Based on the above example, we can form a rule for solving a system of linear inequalities:
To solve a system of linear inequalities, you need to solve each inequality separately, and specify the set of solutions satisfying each inequality as a numerical interval.
Example 2. Solve the system of inequalities 
Solutions of the first inequality are all numbers greater than 17. Solutions of the second inequality are all numbers greater than 12.
Solutions of both inequalities are all numbers greater than 17.
Let us represent the set of solutions of the system on the coordinate line and write the answer as a numerical interval.
First, let us mark the boundaries of both inequalities on the coordinate line:
On the upper region, mark the set of solutions to the first inequality x > 17
On the lower region, mark the set of solutions to the second inequality x > 12
We are interested in the area that is marked with strokes on both sides. This is the area where the solutions of the system. You can see that this region is located in the interval from 17 to plus infinity. Let us write down the answer as a numerical interval:
x ∈ ( 17 ; +∞ )
Example 3. Solve a system of inequalities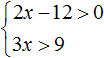 
Solve each inequality individually. You can do this within the system. If you have trouble solving each inequality, be sure to review the previous lesson
We obtained the system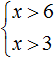 
. This completes the solution. It remains to represent the set of solutions of the system on the coordinate line and write the answer in the form of a numerical interval.
As in the last example, first mark the boundaries of both inequalities, then mark the set of solutions of each inequality (x > 6 and x > 3). The area of the coordinate line marked on both sides will be the interval in which the set of solutions of the system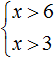
x ∈ ( 6 ; + ∞ )
Example 4. Solve the system of inequalities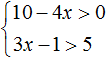 
Let's solve each inequality separately:
Let us represent the set of solutions of system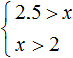 
on the coordinate line and write the answer as a numerical interval:
Example 5. Solve an inequality 
Let's solve each inequality separately:
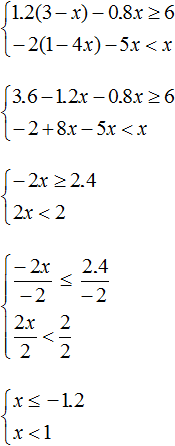
Let us represent the set of solutions of system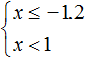 
on the coordinate line and write the answer as a numerical interval:
When there are no solutions
If the inequalities that make up the system have no solutions in common, then the system is said to have no solutions.
Example 1. Solve an inequality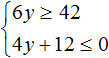 
Let's solve each inequality separately:
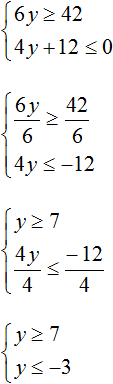
Solutions of the first inequality are all numbers greater than 7, including the number 7. Solutions of the second inequality are all numbers that are less than -3, including the number -3.
You can see that these inequalities have no solutions in common. You can see this clearly on the coordinate line. Mark on it the set of solutions for each inequality:
On the coordinate line there are no regions that are marked with strokes on both sides. This indicates that the inequalities y ≥ 7 and y ≤ -3 have no general solutions. So the system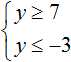 
has no solutions.
And if the given equivalent system 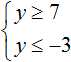has no solutions, then the original system 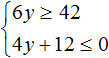has no solutions either.
Answer: no solutions.
Example 2. Solve a system of inequalities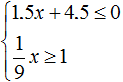 
Let's solve each inequality separately:
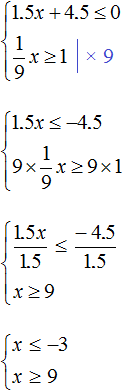
Draw the set of solutions to the inequalities x ≤ -3 and x ≥ 9 on the coordinate line:
We see that on the coordinate line there are no areas that are marked with dashes on both sides. So the inequalities x ≤ -3 and x ≥ 9 have no general solutions. This means that the system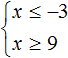 
has no solutions.
And if the given equivalent system 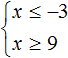has no solutions, then the original system 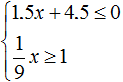has no solutions either.
Answer: no solutions.
Example 3. Solve a system of inequalities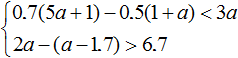 
Let's solve each inequality separately:
We obtain the inequalities 0 < -0.2 and a > 5. The first inequality is not true and has no solutions. Solutions of the second inequality a > 5 are all numbers that are greater than 5. But since the first inequality will not be true for any a, we can conclude that the inequalities have no common solutions. This means that the original system 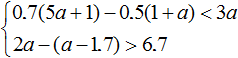has no solutions.
Answer: no solutions.
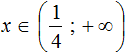
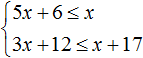
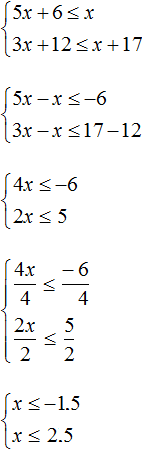
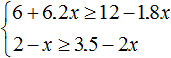
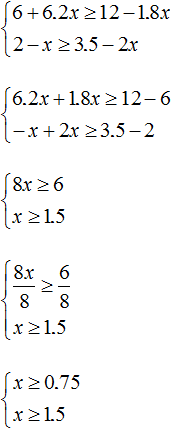
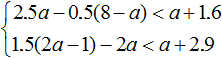
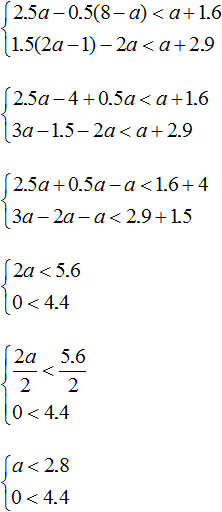
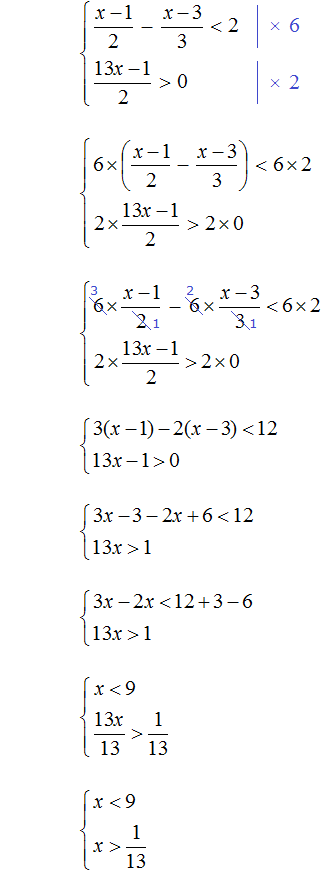
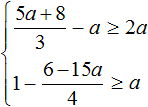
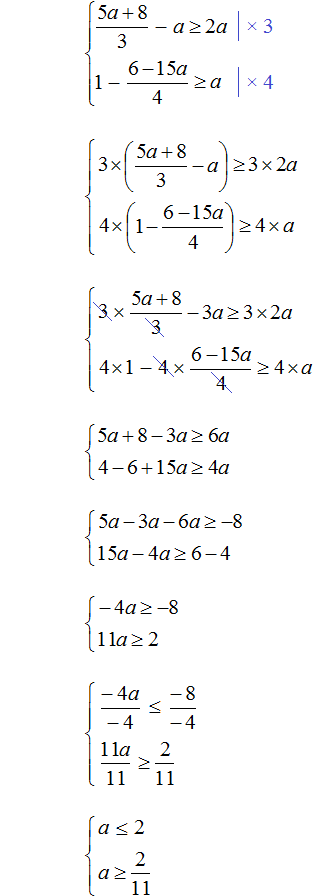
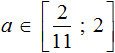
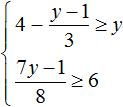
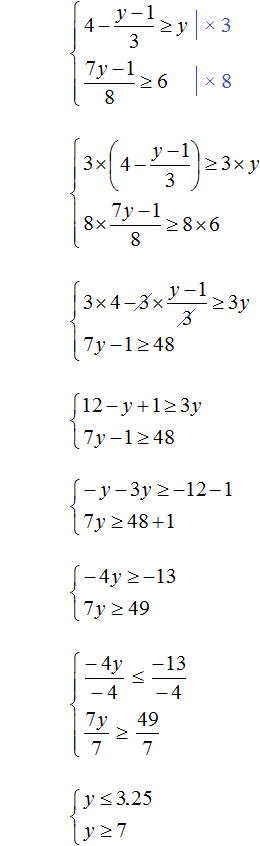
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.