A power with integer exponent is a power whose exponent is any integer.
In the last lesson we studied the power with a natural exponent. This type of power is also a power with an integer because natural numbers refer to integers.
Also, we looked at the power of a power whose exponent is 0. This type of power is also a power with an integer exponent, since 0 refers to integers.
Let us consider another kind of power with an integer exponent, namely, the exponent of which is a negative integer. These powers look like this:
2−2, 10−7, a−8
From now on, we will call any power with a natural, zero, or integer negative exponent a power with an integer exponent.
Calculation rule
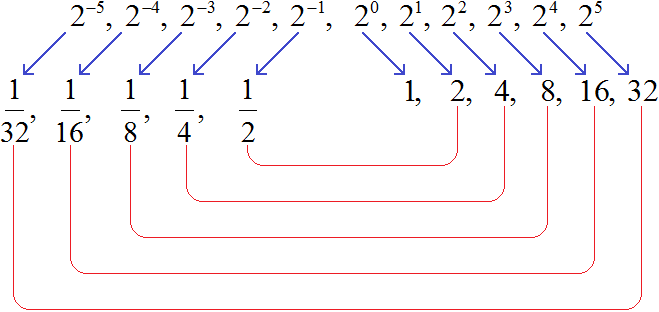
Consider the following sequence of powers:
20, 21, 22, 23, 24, 25
The first power in this sequence is 20. The previous power with an integer will already have a negative exponent and look like 2−1.
2−1, 20, 21, 22, 23, 24, 25
And the previous power with an integer exponent, which is located before 2−1, will be power 2−2
2−2, 2−1, 20, 21, 22, 23, 24, 25
Let's continue this sequence in the direction of powers with negative integer exponents:
2−5, 2−4, 2−3, 2−2, 2−1, 20, 21, 22, 23, 24, 25
Now let's try to calculate these powers. The powers with natural exponents and powers with an exponent of 0 are easy to calculate:
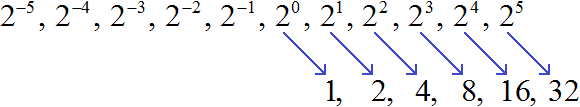
And how do you calculate powers with negative exponents? First, let's discuss a few regularities.
The number is raised to the negative power in a slightly different way. It should be understood that if the number is increased when it is raised to the positive power, then it is decreased when it is raised to the negative power.
If we take any number n, and start increasing its power in sequence, we get a sequence of numbers in which each number is n times smaller than the next one.
For example, let's take the number 2. Starting from zero we will consistently increase its exponent:
20, 21, 22, 23, 24, 25
Let us calculate these powers:
1, 2, 4, 8, 16, 32
We obtained a sequence of numbers in which each number is less than the next number by a factor of 2. Then it is logical to assume that the number located before one will be half as many as one. It can be obtained by dividing 1 by 2
![]()
Let's go back to our original sequence, where we calculated powers. It turns out that the power of 2−1 we have calculated. It is equal to the rational number ![]()
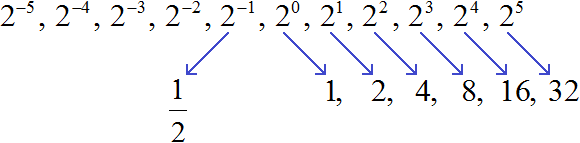
The previous one after the number ![]() must be half as much as
must be half as much as ![]() . To get it, divide
. To get it, divide ![]() by 2
by 2
![]()
We got ![]() . This is the value of power 2−2
. This is the value of power 2−2
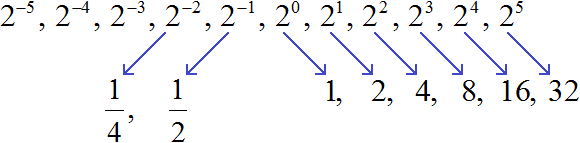
Continue dividing by 2 to get the values of the remaining powers with integer negative exponents:
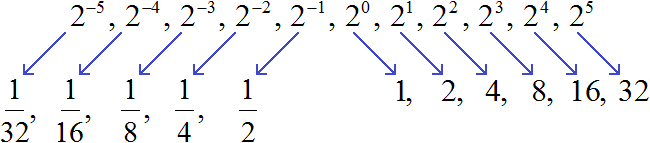
Note that in this sequence, the values of powers with negative exponents are inverse numbers to the values of powers with natural exponents:
For example, the value of the power of 22 is 4. And the value of the power of 2−2 is ![]() . The numbers 4 and
. The numbers 4 and ![]() are inverse of each other. And the powers of 22 and 2−2 differ only in that they have opposite exponents.
are inverse of each other. And the powers of 22 and 2−2 differ only in that they have opposite exponents.
We can conclude that to calculate the power with a negative exponent, we need to write a fraction with one in the numerator and the same power with the opposite exponent in the denominator. Let's show this using an example of the power of 2−2
![]()
Calculate the power in the denominator:
![]()
Thus, to calculate the power of the form a−n, you can use the following rule:
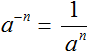
This rule can be proved using the rule of division of powers with equal bases. Suppose, for example, we need to calculate the expression 23 : 25. Let us write this division as a fraction
![]()
Let's use the rule of division of powers with equal bases:
![]()
We obtained the power with a negative exponent 2−2. Earlier we found out that its value is ![]() . To be sure of this, let's try to calculate the expression
. To be sure of this, let's try to calculate the expression ![]() as usual, without using the rule of division of powers:
as usual, without using the rule of division of powers:
![]()
We obtained a rational number ![]() . Let us reduce it by 8. Then we get
. Let us reduce it by 8. Then we get ![]()
![]()
Example 2. Find the value of expression 9−2
Use the rule of calculating a power with a negative integer exponent:
![]()
Example 3. Find the value of expression 3−3
![]()
It is important to know that the ![]() rule works only when a ≠ 0.
rule works only when a ≠ 0.
Indeed, if a equals zero, then the denominator is 0, and one cannot divide by zero.
Example 4. Find the value of expression ![]()
Example 5. Find the value of expression 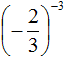

When you raise fractions to the negative power, you can use formula 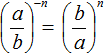 . Let us solve the previous two examples using this formula:
. Let us solve the previous two examples using this formula:
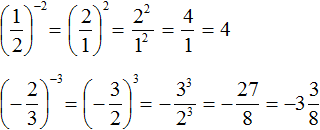
It is desirable to be able to raise fractions to the negative power both with and without a formula.
Identical transformations
All identical transformations that we considered in the study of the power with a natural exponent also hold for powers with integer negative exponents.
For example, to represent the expression 2−1 × 2−3 as a power, you can use the basic property of power:
2−1 × 2−3 = 2−1 + (−3) = 2−4
Example 2. Find the value of expression 5−15 × 516
Let us use the basic property of the power:
5−15 × 516 = 5−15 + 16 = 51 = 5
or:
![]()
We see that the first version of the solution is much easier and more convenient.
Example 3. Find the value of expression (10−4)−1
Let's use the rule of raising the power of power
(10−4)−1 = 10−4 × (−1) = 104 = 10000
Example 4. Find the value of expression ![]()
Let's represent the number base 10 as a product of 2 × 5. Then the numerator will be (2 × 5)−6
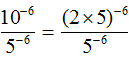
In the numerator, we apply the rule of exponentiation of the product:
![]()
Let's reduce the resulting fraction by 5−6
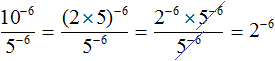
Let's calculate the power of 2−6
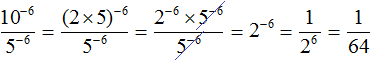
Raising the power from the denominator to the numerator and vice versa
If the denominator of a fractional expression contains a power, that power can be raised to the numerator by reversing the sign of the exponent. The value of the expression does not change. This transformation is sometimes used when simplifying expressions.
Consider the following equality:
![]()
This equation is true because expression ![]() equals 20, and any number to the power of zero is one.
equals 20, and any number to the power of zero is one.
Let us try to raise the power 22 from the denominator to the numerator by changing the sign of the index of this power to the opposite. In this case, connect the raised power and the power that was located in the numerator with the multiplication sign:
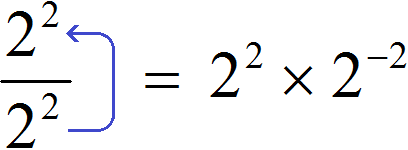
We obtained the expression 22 × 2−2. To calculate it, we use the basic property of the power:
22 × 2−2 = 22 + (−2) = 20 = 1
The result is the same as before. So the value of the expression has not changed. How does this work?
If we swap the left and right parts of equality ![]() , we obtain equality
, we obtain equality ![]() . This makes it possible to replace in expressions a fraction of the form
. This makes it possible to replace in expressions a fraction of the form ![]() with an identically equal expression a-n.
with an identically equal expression a-n.
Now let's represent expression ![]() as product
as product ![]() . That is, replace division with multiplication. Recall that in replacing division with multiplication, the dividend is multiplied by the inverse of the divisor. And the inverse of the divisor in this case is the fraction
. That is, replace division with multiplication. Recall that in replacing division with multiplication, the dividend is multiplied by the inverse of the divisor. And the inverse of the divisor in this case is the fraction ![]()
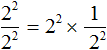
Now let's use rule ![]() . In product
. In product ![]() , replace fraction
, replace fraction ![]() with the identically equal expression 2−2
with the identically equal expression 2−2
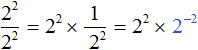
Next, as before, we apply the main property of the power:
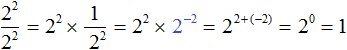
The result is the same as 1.
In the same way, you can drop the power from the numerator to the denominator, changing the sign of the exponent of that power to the opposite.
Consider the expression ![]() . To find its value, use the rule of division of powers with equal bases. The result is
. To find its value, use the rule of division of powers with equal bases. The result is ![]()
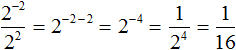
Now let's try to solve this example by dropping the power of 2−2 from the numerator to the denominator, changing the sign of the exponent of this power to the opposite. In this case, the power of 2−2 omitted and the power that was in the denominator will be connected by the multiplication sign. And the numerator will remain one:
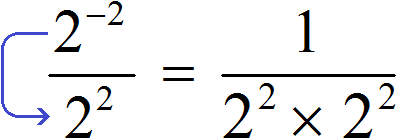
Further calculation is not too difficult:
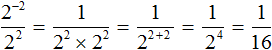
As in the previous example, the expression ![]() can be represented as the product
can be represented as the product ![]()
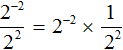
This explains the appearance of the one in the numerator after the power of 2−2 has been dropped in the denominator.
There can be more than one power transferable to the denominator or to the numerator. For example, the denominator of fraction ![]() contains powers 32, a3, b4. Transfer these powers to the numerator by reversing the signs of their exponents. The result is the expression 3−2a−3b−4..
contains powers 32, a3, b4. Transfer these powers to the numerator by reversing the signs of their exponents. The result is the expression 3−2a−3b−4..
Example 2. Raise powers from the denominator of the fraction ![]() to the numerator
to the numerator
![]()
Example 3. Raise powers from the denominator of the fraction ![]() to the numerator
to the numerator
![]()
Example 4. Raise powers from the denominator of the fraction ![]() to the numerator
to the numerator
![]()
Example 5. Lower the power from the numerator of fraction ![]() to the denominator
to the denominator
![]()
Example 6. Lower the power from the numerator of fraction ![]() to the denominator, and raise the power from the denominator to the numerator
to the denominator, and raise the power from the denominator to the numerator
![]()
It is not necessary to represent fraction ![]() as product of
as product of ![]() . If we omit this notation, this example can be solved shorter:
. If we omit this notation, this example can be solved shorter:
![]()
Example 7. In fraction  , transfer from the denominator to the numerator only those powers that have negative exponents:
, transfer from the denominator to the numerator only those powers that have negative exponents:
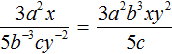
Example 8. Present the product 3x−5 as a fraction without a negative exponent.
Rewrite the product 3x−5 with the multiplication sign:
3 × x−5
Let's leave factor 3 unchanged, and replace the factor x−5 with an identically equal fraction ![]() .
.
![]()
Now, according to the rule of multiplication of a whole number by a fraction, multiply factor 3 into the numerator of the fraction ![]() . The result is a fraction
. The result is a fraction ![]()
![]()
Example 9. Present the product 3(x + y)−4 as a fraction containing no power with a negative exponent.
The expression consists of factors 3 and (x + y)−4. Leave the factor 3 unchanged, and replace the factor (x + y)−4 with an identically equal fraction
![]()
![]()
Now multiply multiplier 3 by the numerator of the fraction ![]() . The result is the fraction
. The result is the fraction ![]()
![]()
Example 10. Represent a fraction ![]() as a product.
as a product.
To solve this example, simply raise the power of x2 to the numerator by reversing the sign of the exponent of that power:
![]()
As in the previous examples, the fraction ![]() could be represented as the product of
could be represented as the product of ![]() . Then using the
. Then using the ![]() rule, replace the factor
rule, replace the factor ![]() with an identically equal factor x−2.
with an identically equal factor x−2.
![]()
Example 11. Present the fraction 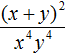 as a product.
as a product.
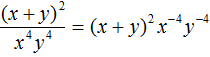
Example 12. Find the value of the expression 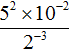
Raise power 2−3 from the denominator to the numerator, and lower power 10−2 from the numerator to the denominator:
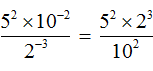
Calculate the values of the powers contained in the numerator and denominator:
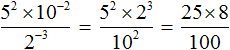
Let's reduce the resulting fraction by 25. Then we are left with a fraction ![]() , the value of which is 2.
, the value of which is 2.
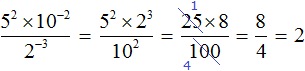
And if we didn't raise the power 2−3 in the numerator, and didn't lower the power 10−2 in the denominator, but calculated each power separately, we wouldn't have a very compact solution:
Raising the number 10 to the integer negative power
The number 10 is raised to the negative power in the same way as other numbers. For example:
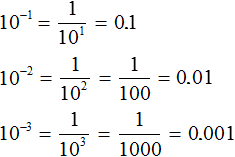
Note that the number of zeros that appear in the answer is equal to the modulus of the exponent of the original power. For example, to the power of 10−2, the modulus of the exponent is 2. This means that the answer will contain two zeros. So it is:
![]()
To raise the number 10 to the negative power, you need to write before the unit the number of zeros equal to the modulus of the exponent of the original power.
The first zero should be followed by a period. Examples:
10−4 = 0.0001
10−5 = 0.00001
10−6 = 0.000001
Representation of the numbers 0.1, 0.01, 0.001 as a power with base 10
To represent the numbers 0.1, 0.01, 0.001 as a power with base 10, you need to write the base of 10, and as the index specify a negative index, whose module is equal to the number of zeroes of the original number.
Let's represent the number 0.1 as a power with base 10. We see that the number 0.1 has one zero. So, the number 0.1 as a power with base 10 will be represented as 10−1. The exponent of the power 10−1 is equal to -1. The module of this exponent is equal to the number of zeros in the number 0.1
0.1 = 10−1
The number 0.1 is the result of dividing ![]() , and this fraction is the value of the power 10−1.
, and this fraction is the value of the power 10−1.
Example 2. Present the number 0.01 as a power with base 10.
The number 0.01 has two zeros. So, the number 0.01 as a power with base 10 will be represented as 10−2. The exponent of the power 10−2 is -2. The modulus of this exponent is equal to the number of zeroes in the number 0.01
0.01 = 10−2
The number 0.01 is the result of dividing ![]() , that is
, that is ![]() , and this fraction is the value of the power 10−2.
, and this fraction is the value of the power 10−2.
Example 3. Present the number 0.001 as a power with base 10.
0.001 = 10−3
Example 4. Present the number 0.0001 as a power with base 10.
0.0001 = 10−4
Example 5. Present the number 0.00001 as a power with base 10.
0.00001 = 10−5
Standard number view
Write the number 2 000 000 as the product of 2 and 1 000 000
2 × 1 000 000
The factor 1 000 000 can be replaced by the power of 106
2 × 106
This type of notation is called a standard number view. The standard number view allows you to write both large and small numbers in a compact form.
For example, a small number 0.005 can be written as the product of 5 and a decimal 0.001.
5 × 0.001
The decimal 0.001 can be replaced by a power with 10−3
5 × 10−3
So, the number 0.005 in standard view will look like 5 × 10−3
0.005 = 5 × 10−3
From the standard view of a number, we can calculate the original number. For example, if we write the number 2 000 000 in standard form, we get the product 2 × 106. If we calculate this product, we get 2 000 000 again
2 × 106 = 2 × 1 000 000 = 2 000 000
And when writing the number 0.005 in standard view, we got the product of 5 × 10−3. If we calculate this product, we get 0.005
![]()
That is, when writing a number in standard view, you need to write it in such a way as to preserve its original value.
The standard view of a number is an entry of the form a × 10n, where 1 ≤ a < 10 and n is an integer.
The number a is the initial number to be written in standard view. It must satisfy the inequality 1 ≤ a < 10. Most often, the original number must be reduced to a form in which the inequality 1 ≤ a < 10 becomes true.
For example, let's represent the number 12 in the standard view. First, check whether the inequality 1 ≤ a < 10 becomes true when we substitute the number 12 for a
1 ≤ 12 < 10
The inequality does not become true. To make the inequality true, let's make the number 12 a form in which it would satisfy the inequality. To do this, move a point in number 12 to the left by one digit:
1.2
The number 12 is converted to 1.2. This number will satisfy the inequality 1 ≤ a < 10
1 ≤ 1.2 < 10
Now our task is to write down the product a × 10n. We have solved the number a - this number will be 1.2. But how do we find the power with base 10?
After moving the dot one digit to the left, the number 12 has lost its original meaning. The point one digit to the left is moved when the number is divided by 10. To restore the original value of the number, the point must be moved back to the right side by one digit, that is, multiply the number 1.2 by 10.
So, to write the number 12 in standard view, we need to represent it as a product of 1.2 × 10¹.
12 = 1.2 × 10¹
Example 2. Write the number 0.5 in the standard view.
The number 0.5 does not satisfy the inequality 1 ≤ a< 10, so move the point in this number one digit to the right. As a result, we get number 5, which satisfies the inequality 1 ≤ a< 10.
Now write down a product of the form a × 10n. The number a in this case is 5. And the power with base 10 should be chosen so that the product a × 10n becomes equal to the number 0.5. The number 0.5 is obtained by multiplying the number 5 by the factor 0.1, which is presented as the power of 10−1. The result will be the following notation:
0.5 = 5 × 10−1
Example 3. Write the number 652 000 in the standard view.
The number 652 000 does not satisfy the inequality 1 ≤ a< 10, so move the point in this number five digits to the left. As a result, we get the number 6.52000, which satisfies the inequality 1 ≤ a< 10.
Now write down the product of the form a × 10n. The number a in this case is 6.52000. And the power with base 10 must be chosen so that the product a × 10n becomes equal to the number 652 000. You can get the number 652 000 if you multiply the number 6.52000 by 100 000, which is the power of 105. The result is the following notation:
652 000 = 6.52000 × 105
The zeros at the end of the decimal 6.52000 can be discarded. Then we get a more compact notation:
652 000 = 6.52 × 105
Example 5. Write the number 1 024 000 in the standard view.
The number 1 024 000 does not satisfy the inequality 1 ≤ a< 10, so move the point in this number six digits to the left. As a result, we obtain the number 1.024000, which satisfies the inequality 1 ≤ a< 10.
Now write down a product of the form a × 10n. The number a in this case is 1.024000 . And the power with base 10 must be chosen so that the product a × 10n is equal to the original number 1 024 000. The number 1 024 000 is obtained if 1 024 000 is multiplied by 1 000 000, which is the power of 106. The result will be the following notation:
1 024 000 = 1.024000 × 106
The zeros at the end of the decimal 1.024000 can be discarded:
1 024 000 = 1.024 × 106
You can only discard those zeros which are located at the end and after which there are no other digits larger than zero. In the example above, only three zeros were discarded, and the zero located between the point and the digit 2 was preserved, despite the fact that it was also located after the point.
Example 6. Write the number 0.000325 in the standard view.
Move a point in this number so that it satisfies the inequality 1 ≤ a< 10. As a result, we obtain the number 3.25
Now write down the product of the form a × 10n. The number a in this case is 3.25. And the power with base 10 must be chosen so that the product of a × 10n is equal to the original number 0.000325. The number 0.000325 is obtained if the number 3.25 is multiplied by the factor 0.0001, which is presented as the power of 10−4. The result is the following notation:
0.000325 = 3.25 × 10−4
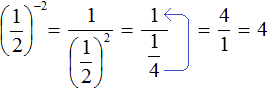

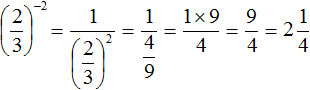
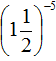
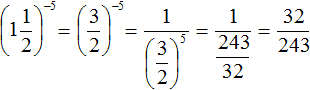
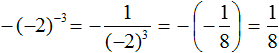
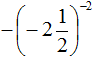
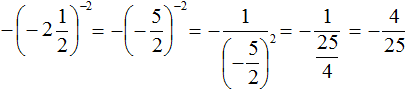
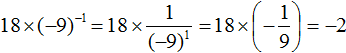
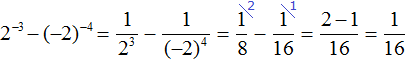
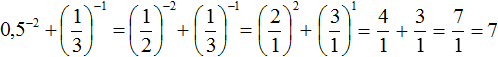
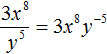
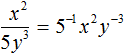
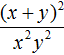 as a product.
as a product.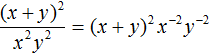
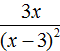 as a product.
as a product.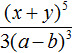 as a product.
as a product.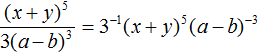
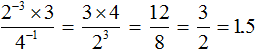
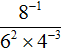 .
.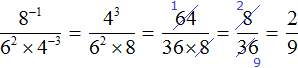
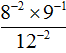 .
.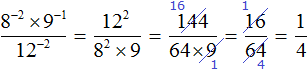
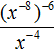 .
.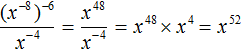
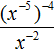 .
.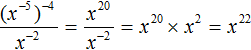
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.