The subject of rational numbers is quite vast. You can talk about it endlessly and write entire works, each time being surprised by new tricks.
To avoid future mistakes, in this lesson we will delve a little deeper into the subject of rational numbers, learn from it, and move on.
What are Rational Numbers
A rational number is a number that can be represented as a fraction ![]() , where a is the numerator of the fraction and b is the denominator of the fraction. And b must not be zero, because division by zero is not allowed.
, where a is the numerator of the fraction and b is the denominator of the fraction. And b must not be zero, because division by zero is not allowed.
Rational numbers include the following categories of numbers:
- integers (e.g. -2, -1, 0 1, 2, etc.)
- fractions (e.g.
 ,
,  ,
,  , etc.)
, etc.)
- mixed numbers (e.g.
 ,
,  ,
,  , etc.)
, etc.)
- decimals (e.g. 0,2, etc.)
- recurring decimals (e.g. 0,(3), etc.)
Each number in this category can be represented as a fraction ![]() .
.
Example 1. An integer 2 can be represented as a fraction ![]() . So number 2 refers not only to integers but also to rational numbers.
. So number 2 refers not only to integers but also to rational numbers.
Example 2. The mixed number ![]() can be represented as a fraction
can be represented as a fraction ![]() . This fraction is obtained by converting the mixed number into an improper fraction
. This fraction is obtained by converting the mixed number into an improper fraction
![]()
So the mixed number ![]() is a rational number.
is a rational number.
Example 3. A decimal fraction 0.2 can be represented as a fraction ![]() . This fraction is obtained by converting the decimal fraction 0.2 to a regular fraction. If you have difficulty at this point, review the topic of decimals.
. This fraction is obtained by converting the decimal fraction 0.2 to a regular fraction. If you have difficulty at this point, review the topic of decimals.
Since the decimal 0.2 can be represented as a fraction ![]() , it is also a rational number.
, it is also a rational number.
Example 4. An recurring decimals 0. (3) can be represented as a fraction ![]() . This fraction is obtained by converting a pure periodic fraction into an ordinary fraction. If you have some difficulties at this point, repeat the topic of recurring decimals.
. This fraction is obtained by converting a pure periodic fraction into an ordinary fraction. If you have some difficulties at this point, repeat the topic of recurring decimals.
Since the recurring decimals 0. (3) can be represented as a fraction ![]() , it is also a rational number.
, it is also a rational number.
In the future, all numbers that can be represented as fractions, we will name - rational numbers.
Rational numbers on the number line
We looked at the number line when we studied negative numbers. Recall that this is a line on which many numbers lie. It looks like this:
![]()
This figure shows a small fragment of the number line from -5 to 5.
Marking integers like 2, 0, and -3 on the coordinate line is not too difficult.
Things are much more interesting with the other numbers: fractions, mixed numbers, decimals, etc. These numbers lie between integers and there are infinitely many of them.
For example, note on the number line the rational number ![]() . This number is located exactly between zero and one
. This number is located exactly between zero and one

Let's try to understand why the fraction ![]() is suddenly placed between zero and one.
is suddenly placed between zero and one.
As mentioned above, between the integers there are other numbers too - fractions, decimals, mixed numbers, etc. For example, if you zoom in on a segment of the number line from 0 to 1, you can see the following picture
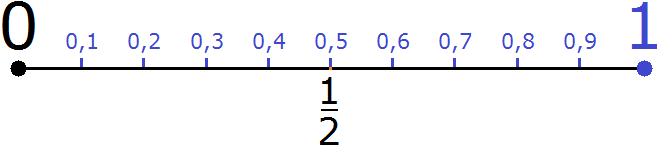
You can see that between the integers 0 and 1 there are other rational numbers. Here you can see our fraction ![]() , which is located in the same place as the decimal 0.5. Careful consideration of this figure answers the question of why the fraction
, which is located in the same place as the decimal 0.5. Careful consideration of this figure answers the question of why the fraction ![]() is located exactly there.
is located exactly there.
Fraction ![]() means to divide 1 by 2. And if we divide 1 by 2, we get 0.5
means to divide 1 by 2. And if we divide 1 by 2, we get 0.5
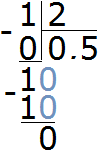
The decimal 0.5 can also be presented as other fractions. We know from the basic property of fractions that if the numerator and denominator of a fraction are multiplied or divided by the same number, the value of the fraction will not change.
If we multiply the numerator and denominator of ![]() by any number, such as 4, we get a new fraction
by any number, such as 4, we get a new fraction ![]() , and this fraction, like
, and this fraction, like ![]() , is 0.5
, is 0.5
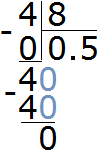
This means that on the number line the fraction ![]() can be placed in the same place as the fraction
can be placed in the same place as the fraction ![]() .
.

Example 2. Let's try to place the rational number ![]() on the number line. This number is located exactly between the numbers 1 and 2
on the number line. This number is located exactly between the numbers 1 and 2

The value of the fraction ![]() is 1.5
is 1.5
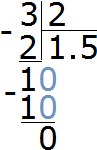
If we zoom in on a segment from 1 to 2, we see the following picture:
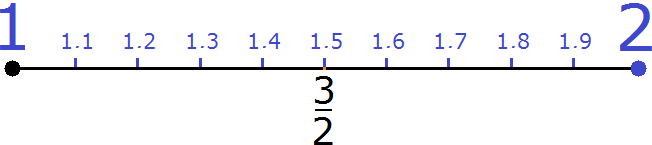
You can see that between the integers 1 and 2 there are other rational numbers, which are familiar to us decimal fractions. Here you can see our fraction ![]() , which is located in the same place as the decimal 1.5.
, which is located in the same place as the decimal 1.5.
We zoomed in on certain segments on the number line to see the rest of the numbers lying on that segment. As a result, we found decimals that had one digit after the point.
But these were not the only numbers lying on these segments. The numbers lying on the coordinate line are infinitely many.
It is not difficult to guess that between the decimals that have one digit after the point, there are other decimal fractions that have two digits after the point. In other words, hundredths of a segment.
For example, let's try to see the numbers that lie between the decimals 0.1 and 0.2
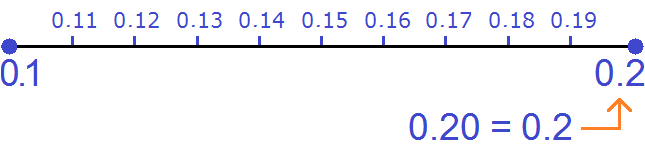
Another example. Decimals with two digits after the point and lying between zero and the rational number 0.1 look like this:
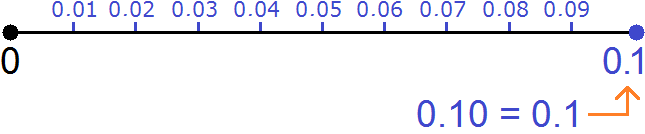
Example 3. Mark the rational number ![]() on the number line. This rational number will be located very close to zero
on the number line. This rational number will be located very close to zero

The value of the fraction ![]() is 0.02
is 0.02
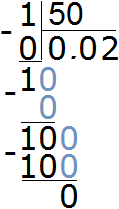
If we increase the segment from 0 to 0.1, we see exactly where the rational number ![]() is located
is located

You can see that our rational number ![]() is located in the same place as the decimal 0.02.
is located in the same place as the decimal 0.02.
Example 4. Mark on the number line the rational number 0. (3)
The rational number 0. (3) is an recurring decimals. Its fractional part never ends, it is infinite
0.33333.... and so on to infinity...
And since the number 0.(3) has a fractional part that is infinite, this means that we cannot find the exact place on the coordinate line where this number is located. We can only indicate this place approximately.
The rational number 0.33333... will lie very close to the usual decimal 0.3

This figure does not show the exact location of the number 0.(3). It is only an illustration to show how close the periodic fraction 0.(3) can be located to decimal 0.3.
Example 5. Mark the rational number ![]() on the coordinate line. This rational number will be in the middle between numbers 2 and 3
on the coordinate line. This rational number will be in the middle between numbers 2 and 3

![]() is 2 (two integers) and
is 2 (two integers) and ![]() (one second). The fraction
(one second). The fraction ![]() are also called "halves". So we marked two whole segments on the number line and another half segment.
are also called "halves". So we marked two whole segments on the number line and another half segment.
If we convert the mixed number ![]() to an improper fraction, we get the fraction
to an improper fraction, we get the fraction ![]() . This fraction on the number line will be located in the same place as the fraction
. This fraction on the number line will be located in the same place as the fraction ![]()

The value of the fraction ![]() is 2.5
is 2.5
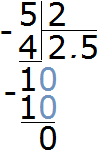
If we zoom in the section of the number line from 2 to 3, we see the following picture:
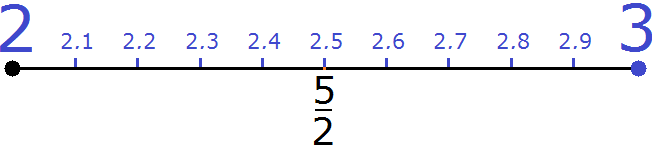
You can see that our rational number ![]() is located in the same place as the decimal 2.5
is located in the same place as the decimal 2.5
Minus before a rational number
In the previous lesson, called multiplication and division of integers, we learned how to divide integers. Both positive and negative numbers could be the dividend and the divisor.
Consider the simplest expression
(−6) : 2 = −3
In this expression, the dividend (-6) is a negative number.
Now consider the second expression
6 : (−2) = −3
Here the negative number is already the divisor (-2). But in both cases we get the same answer -3.
Given that any division can be written as a fraction, we can write the above examples as fractions as well:
![]()
![]()
And since in both cases the value of the fraction is the same, the minus in either the numerator or the denominator can be made common by putting it in front of the fraction
![]()
![]()
Therefore, we can put an equal sign between the expressions ![]() and
and ![]() and
and ![]() because they carry the same meaning
because they carry the same meaning
![]()
Later on, when we work with fractions, if we encounter minus in the numerator or denominator, we will make that minus common by putting it in front of the fraction.
Opposite rational numbers
Like an integer, a rational number has its opposite.
For example, for a rational number ![]() , the opposite number is
, the opposite number is ![]() . It is located on the number line symmetrically to the location of
. It is located on the number line symmetrically to the location of ![]() relative to the origin. In other words, both these numbers are equidistant from the origin
relative to the origin. In other words, both these numbers are equidistant from the origin
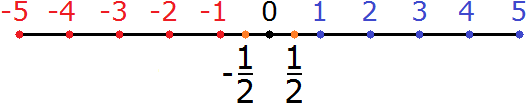
Conversion of mixed numbers into improper fractions
We know that if we want to convert a mixed number into an improper fraction, we need to multiply the integer part by the denominator of the fractional part and add it to the numerator of the fractional part. The resulting number will be the numerator of the new fraction, and the denominator remains the same.
For example, let's convert the mixed number ![]() to an improper fraction
to an improper fraction
Multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part:
(2 × 2) + 1
Let's calculate this expression:
(2 × 2) + 1 = 4 + 1 = 5
The resulting number 5 will be the numerator of the new fraction, and the denominator will remain the same:
![]()
This procedure is written in full as follows:
![]()
To return the original mixed number, just highlight the integer part in the fraction ![]()
![]()
But this method of converting a mixed number into an improper fraction is applicable only if the mixed number is positive. For a negative number, this method will not work.
Consider the fraction ![]() . We distinguish the integer part of the fraction. We get
. We distinguish the integer part of the fraction. We get ![]()
![]()
To return the original fraction ![]() , we need to convert the mixed number
, we need to convert the mixed number ![]() into an improper fraction. But if we use the old rule, which is to multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number, we get the following contradiction:
into an improper fraction. But if we use the old rule, which is to multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number, we get the following contradiction:
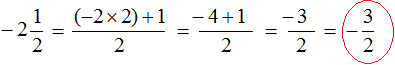
We got a fraction of ![]() , and we should have gotten a fraction of
, and we should have gotten a fraction of ![]() .
.
We conclude that the mixed number ![]() is incorrectly converted into an improper fraction:
is incorrectly converted into an improper fraction:
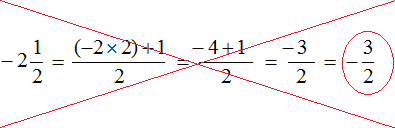
To convert a negative mixed number into an improper fraction correctly, multiply the integer part by the denominator of the fractional part, and subtract the numerator of the fractional part from the resulting number. In this case, everything will fall into place
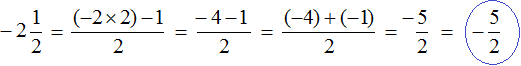
The negative mixed number ![]() is the opposite of the mixed number
is the opposite of the mixed number ![]() . If the positive mixed number
. If the positive mixed number ![]() is on the right side and looks like this
is on the right side and looks like this

then the negative mixed number ![]() will be located in the left part symmetrically
will be located in the left part symmetrically ![]() relative to the origin
relative to the origin

And while ![]() reads "two integers and one second,"
reads "two integers and one second," ![]() reads "minus two and a half". Because the numbers -2 and
reads "minus two and a half". Because the numbers -2 and ![]() are on the left side of the coordinate line, they are both negative.
are on the left side of the coordinate line, they are both negative.
Any mixed number can be written in expanded form. A positive mixed number ![]() is written as
is written as ![]() in expanded form.
in expanded form.
And a negative mixed number ![]() is written as
is written as ![]()
Now we can understand why the mixed number ![]() is located on the left side of the number line. The minus before the two indicates that we moved from zero two steps to the left, as a result we are at the point where the number -2
is located on the left side of the number line. The minus before the two indicates that we moved from zero two steps to the left, as a result we are at the point where the number -2
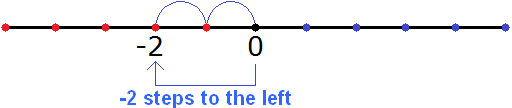
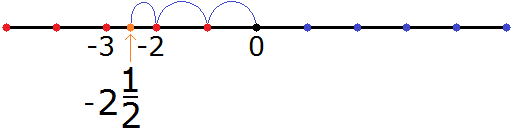
Then, starting from the number -2, we move another ![]() step to the left. And since the value of
step to the left. And since the value of ![]() is -0.5, our step is half of the full step.
is -0.5, our step is half of the full step.

We end up in the middle between the numbers -3 and -2
Example 2. Select the integer part of an improper fraction ![]() , then convert the resulting mixed number back to an improper fraction
, then convert the resulting mixed number back to an improper fraction
Let's do the first part of the assignment, namely, isolate the integer part in the improper fraction ![]()
![]()
Perform the second part of the problem, namely, convert the resulting mixed number ![]() to an improper fraction. To do this, multiply the integer part by the denominator of the fractional part and subtract the numerator of the fractional part from the resulting number:
to an improper fraction. To do this, multiply the integer part by the denominator of the fractional part and subtract the numerator of the fractional part from the resulting number:
![]()
If you don't want to get confused and get used to the new rule, you can put the mixed number in parentheses and leave the minus behind the parentheses. Then you can apply the good old rule: multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number.
Let's perform the previous task in this way, namely, to convert the mixed number ![]() into an improper fraction
into an improper fraction
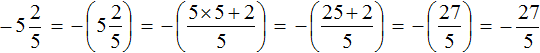
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.