We continue to study elementary math problems. Today we are going to look at a very interesting physical quantity - performance.
Definition and mathematics of Work
"Work" problems usually involve situations such as two people working together to paint a house. We sometimes need to calculate how many people are needed to complete a task within a given time. Alternatively, given a limited number of people, we often need to determine how long it takes to finish a task. Here we deal with the basic math concepts of how to handle these types of problems.
Many of these problems are not realistic - but it's the technique that teachers want you to learn, not the applicability to "real life".
Work is denoted by the capital Latin letter - A.
Productivity
Productivity (power) is the amount of work done per unit of time. A unit is one hour, one minute, or one second. Productivity is denoted by the Latin letter - V
Consider the following example. Two bakers are baking bread. The first baker baked 40 loafs of bread in 10 minutes, and the second 15 loafs in 5 minutes. How do we know which baker worked faster, the first or the second?
The one who bakes more loafs in one minute worked faster. We can say that he has a greater productivity. The following rule is used to find the Productivity:
To find the Productivity, you must divide the work done by the time of work.
Also, you can use the formula:
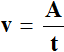
where V - productivity, A - work done, t - time of work.
Let's return to our task. If we know the rule or formula how to calculate the performance, we can determine how many loafs were made per minute.
Let's find the performance of the first baker.
Divide the work he did by the time he spent on it. The work done is the number of loafs he baked, that is, 40, and the time is 10 minutes.
40 : 10 = 4 loafs per minute
Similarly, find the performance of the second baker. Divide 15 by 5
15 : 5 = 3 loafs per minute
4 > 3
The first baker bakes more loafs per minute than the second baker, so his performance is higher. So we conclude that he works faster than the second baker.
You can also use the formula for finding the performance. In this case, the solution is as follows:
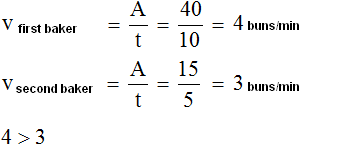
Task 2. Tom needs to read a book with 100 pages in two days. On the first day, he read for 4 hours at a rate of 12 pages per hour. At what rate should he read the rest of the book, if he has 4 hours to do it?
Lets find out how many pages did Tom read the first day. He read 12 pages per hour. He spent 4 hours reading on the first day, so multiply 12 by 4 in order to find how many pages did he read on the first day.
12 × 4 = 48 pages
Let's find out how many pages are left to read. Let's subtract the number of pages he read (48) from the total number of pages (100)
100 - 48 = 52 pages left to read
There are 52 pages left to read. Now find the performance at which Tom can read 52 pages in 4 hours. Let's distribute the 52 pages equally over 4 hours
52 : 4 = 13 pages per hour
Answer: To read the rest of the book in 4 hours, Tom must read it at the rate of 13 pages per hour.
Note. In some sources, the word "performance" may be replaced with the words "speed," "efficiency," "productivity".
Task 3. One pump worked for 4 hours, pumping out 158 buckets of water per hour, and the other pump worked for 3 hours, pumping out 169 buckets of water per hour. Determine which pump pump pumped out more buckets of water.
Solution
Determine how many buckets each pump did fill individually. To do this, multiply their performance by their working time:
158 × 4 = 632 buckets the first pump pumped
169× 3 = 507 buckets the second pump squeezed out
632 > 507
Answer: the first pump pumped out more buckets than the second pump.
Task 4. In 2 hours the pump pumped out 80 liters of water. Determine how many liters it will pump out in 5 hours of such work.
Solution
First, lets determine how many liters of water the pump pumps out in one hour. To do this, divide 80 liters by 2 hours.
80 : 2 = 40 liters per hour.
The pump will pump out 40 liters of water in one hour. In five hours the pump will pump out five times as much.
40 × 5 = 200 liters.
Answer: the pump will pump out 200 liters of water in 5 hours.
If you know the performance and the time of work, you can find the amount of work done. The amount of work done is equal to the performance multiplied by the time of work:
A = v × t
For example, if the baker's performance is 50 loafs per hour, and he worked for 4 hours, then you can find the amount of work done in those 4 hours. To do this, the performance (50 loafs per hour) must be multiplied by the time he worked (4 hours)
50 × 4 = 200 buns (loafs)
If the work and performance are known, you can find the time of work. Working time is equal to the ratio of amount of work to performance:
For example, if a team builds 2 floors per week, you can find out how many weeks will it take to build 8 floors. To determine the time it takes to build eight floors, divide the work done (8 floors) by the performance (2 floors/week):
8 : 2 = 4 weeks.
Or using the formula above:
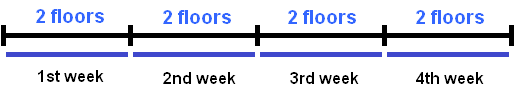
If two stories are built per week, then eight stories will be built in four weeks. In this case, all the work was equal to eight. The performance was equal to two, because by definition, performance is the work done per unit of time-in this case, two floors in a week.
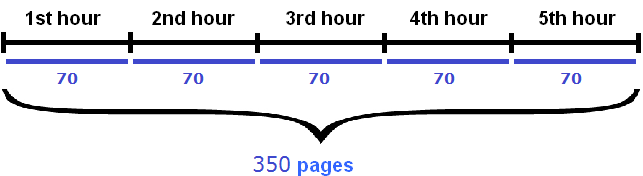
Task 6. The printer is printing at a rate of 70 pages per hour. How many pages will it print in 5 hours?
Solution
If the printer prints 70 pages per hour, it will print 5 times that many in 5 hours:
70 × 5 = 350 pages
Also, the solution can be written using the formula for finding work. In this case, the number of pages printed is the work done:
A = v × t = 70 × 5 = 350 pages
A = 350 pages
Task 7. The printer printed 350 pages in 5 hours. At what performance rate did it work?
Solution
If the printer printed 350 pages in five hours, it printed 
. That is, it performed at a rate of 70 pages per hour:
350 : 5 = 70 pages/hour.
Either using the formula for finding the performance rate:
Task 8. The printer was performing at 70 pages per hour and printed 350 pages. Determine the operating time of the printer.
Solution
The expression "was performing at 70 pages per hour" means that in each hour the printer printed 70 pages. And it continued to do so until it printed 350 pages. Obviously, if we divide the 350 pages by 70, we find out how many hours the printer was on
350 : 70 = 5 ч.
Either by using the formula for finding the time:
Task 9. The secretary printed 48 pages of the manuscript on the first day and 12 pages more on the second day than on the first. She spent 9 hours on all the work on those 2 days. How many hours she worked each of these days if her performance did not change ?
Solution
Determine how many pages the secretary printed on the second day. The condition says that she printed 12 more pages than she did on the first day:
48 + 12 = 60 pages on the second day.
Determine how many pages the secretary printed during the two days:
48 + 60 = 108 pages in two days.
The secretary spent 9 hours on this work. It is also said that her productivity did not change. If we divide the work done (108) by the time done (9), we determine the secretary's performance:
108 : 9 = 12 pages per hour.
Now we can determine how many hours the secretary worked on each of the two days. To do this, we divide in turn the work done on each of the two days by the performance:
48 : 12 = 4 hours the secretary worked on the first day
60 : 12 = 5 hours the secretary worked on the second day.
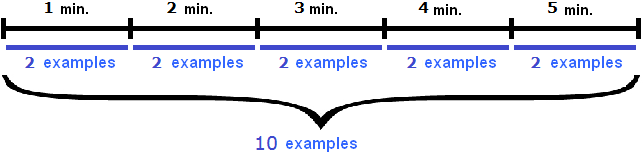
Task 10. John solved 10 examples in 5 minutes. At what performance rate did he solve these examples?
The 10 examples are the work John did. 5 minutes is the time of work. Divide the work done by the time of work and determine John's performance:
10 : 5 = 2 examples per minute.
John's performance is equal to two examples per minute.
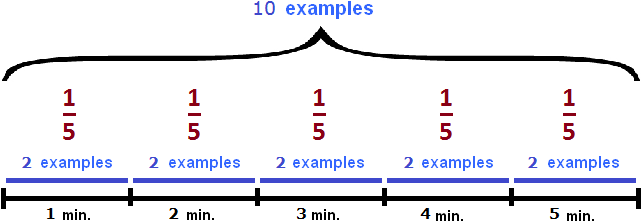
Task 11. John solved several examples in 5 minutes. With what performance did he solve these examples?
This is the same task as the previous one, but the work is not expressed by any number. All that is said is that John did the work in 5 minutes. Therefore, it is not possible to find out the specific performance in this task. But you can use fractions. Let us denote the performed work by one. Then John's performance will be expressed as a fraction - the fraction of examples solved per unit time. If you have studied fractions, you should know what we are talking about.
So, let's denote the work done by a unit:
A = 1
We know that to find performance, the work done must be divided by the time. The time we have is five minutes. Therefore, we divide one by five minutes:
A fraction of expresses some of the work done by John per unit time. If we go back to the previous problem, where the work done was equal to ten examples, and find one fifth of this work, we get 2
Expressing the work accomplished through a unit is often necessary when solving tasks on cooperative work.
Collaborative work tasks
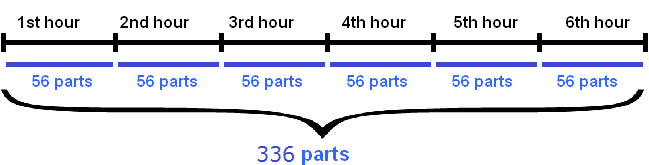
Task 1. The first master makes 64 parts in 2 hours, and the second master makes 72 parts in 3 hours. In how many hours will they produce 336 parts?
In this task we are talking about working together. We need to determine the productivity of both master and find the time in which they will produce 336 parts.
First, let's determine the performance of the first master:
64 : 2 = 32 parts per hour.
Let's determine the performance of the second master:
72 : 3 = 24 parts/hour.
Let's define the joint performance of masters. For this purpose we will add quantity of details which they make separately for a unit of time. That is, let us add their performance:
32 parts/hour + 24 parts/hour = 56 parts/hour.
Together they produce 56 parts in one hour. To know how many hours they will make 336 parts, you need to determine how many times 336 contains 56
336 : 56 = 6 hours
Task 2. The first master can paint a fence in 20 minutes, and the second master can paint a fence in 30 minutes. In how many minutes, working together, can they paint a fence?
Solution
Unlike the previous task, in this problem the work is not expressed by a number. It only says that the first master can do the job in 20 minutes and the second in 30 minutes.
In this situation, we can use fractions. We can denote all the work (painting the fence) by one.
So we denote the work (painting the fence) by one:
A = 1
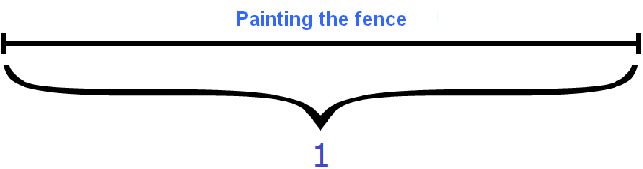
The performance of the first master will be expressed as a fraction of 1/20. That is, in one minute he will paint one twentieth of the fence. One is all the work, and twenty minutes is the time of work. Write down the performance of the first craftsman using the formula for finding performance:
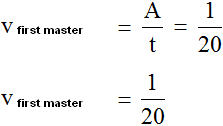
And the performance of the second master will be expressed in fractions of 
. That is, in one minute he will paint one thirtieth of the fence:
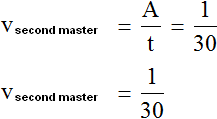
Determine the total performance of the masters. To do this, add the fractions expressing the performance of the first and second masters:
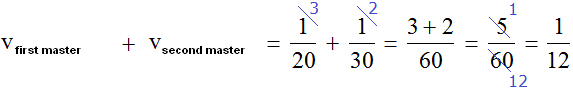
is a fraction expressing the total performance of both masters. That is, in one minute the masters together will paint parts of the fence.
Let's determine the time it takes the masters to paint the fence together. To do this, use the formula for finding the time: divide the work done by the total performance of the masters. The work done is expressed by one unit, and the performance by a fraction of .
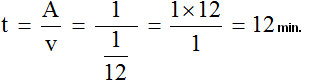
Answer: working together, masters will paint a fence in 12 minutes.
Task 3. The first worker can complete an order in 8 hours, and the second in 6 hours. They worked together for two hours, and only the second worker finished the job. How long did it take to complete this order?
Solution
Let's define all the work by unit
A = 1
Then the first worker can do 
part of the work in one hour, and the second worker can do 
part of the work. And together they can do 
part of the work in one hour
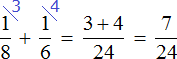
The workers worked together for two hours, so let's multiply the part of the work they did in one hour by 2:
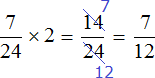
The rest of the work, namely 
, was finished by a second worker:
The second worker could complete parts of the work in one hour. To determine the time in which he completed the remaining pieces of work, use the formula for finding time.
Variable A now equals , variable v equals
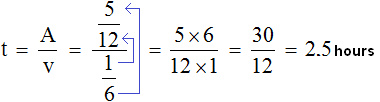
Now determine the total time of the order. The first two hours the workers worked together, the rest of the work was done by the second worker in two and a half hours, so we have 4.5 hours.
2 + 2.5 = 4.5 h.
Answer: It took 4.5 hours to complete the order.
Task 4. One pipe fills the pool in 6 hours, and the other pipe fills the pool in 4 hours. How many hours do the two pipes work together to fill the pool?
Solution
Let's denote the work (filling the pool) by one
A = 1
Then the first pipe will do part of the work in one hour, and the second pipe will do 
part of the work. Working together in one hour they will do 
part of the work:
Determine the time it takes the two pipes to fill the pool, working together:
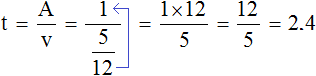
2.4 is two whole hours and four tenths of an hour
2.4 = 2 h + 0.4 h
And four-tenths of an hour is 24 minutes.
60 min. × 0.4 = 24 min.
Answer: both pipes working together will fill the pool in 2 h 24 min.
Exercises
Solution
Let's denote the work by one:
A = 1
Then the first crew will do part of the work, and the second will do part of the work in one hour. Their total performance is equal to the sum of the fractions and :
Let's determine the time in which the two crews will complete the task, working together:
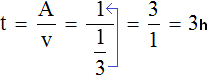
Answer: both crews will complete the job in 3 hours.
Solution
Work in this case is eating a bale of hay. Let us denote it by one:
A = 1
Then the performance of the horse will be expressed by one, the performance of the cow by a fraction 
, sheep performance - fractional . Their joint performance is equal to the following sum:
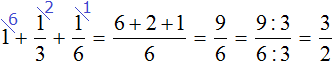
Determine the time it takes a horse, a cow, and a sheep to eat 1 bale of hay:
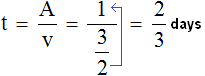
Answer: a horse, a cow, and a sheep will eat 1 bale of hay in 
days or 16 hours.
Solution
The work in this case is the filling of the vessel. Let us denote this work by a unit:
A = 1
The condition says that the vessel is filled by the hose in 12 minutes. It means that part of the vessel will be filled per minute. At the same time it is said that at the same time the faucet of the vessel is opened and water flows out of it, which the vessel is filled with. The water that flows out equals 
part of the vessel, because the condition says that a full vessel is emptied in 20 minutes.
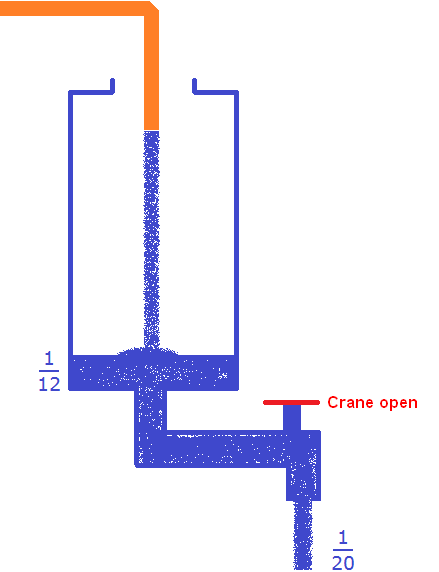
More water enters the vessel than flows out. Fraction is greater than .
Even though some of the water entering the vessel will flow out, the vessel will be replenished by a certain fraction every minute. Let's find out what that part is. To do this, we subtract the part that flows out from the incoming part:
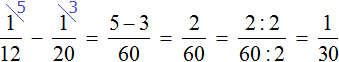
Every minute the vessel will fill by .
Determine the time it takes to fill an empty vessel if you simultaneously open the faucet and pour water into it through the hose:
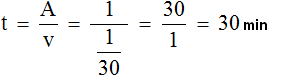
Answer: If you simultaneously open the faucet and pour water into the empty vessel through the hose, it will fill in 30 minutes.
Solution
The work in this case is filling the pool. Let's denote this work by one:
A = 1
The pool performance through the first pipe will be expressed by fraction , through the second pipe by fraction . The joint performance will be expressed by fraction
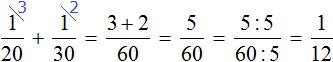
By definition, performance is the work done per unit time. So fraction is the answer to the problem, because we were interested in how much of the pool would fill through both pipes in 1 hour. This can be checked using the formula for finding the work. We have the variable v as , and the variable t as one (one hour). The formula for finding the work will allow us to determine what part of the work will be done in one hour:
Answer: part of the pool will be filled in one hour.
Solution
The task assumes that the excavator worked at the same rate of performance throughout the work. It took 10 hours to do the work. It worked for 8 hours. That means there are still 2 hours left. The 2 hours account for the remaining 50 meters of the trench. If you divide 50 meters by 2, you can determine how many meters the excavator makes in one hour:
50 : 2 = 25 m/h
The excavator was laying 25 meters per hour. It worked for 10 hours. Multiply 25 by 10 to find the total length of the trench:
25 × 10 = 250 m
Answer: The total length of the trench is 250 m.
Solution
For convenience, let's convert the time given in the problem to seconds
6 min 40 sec = 400 sec
8 min = 480 s
13 min 20 s = 800 s
Denote the filling of the bath by one:
A = 1
The performance of the first crane will be expressed as a fraction of 
, the performance of the second crane as a fraction of 
. The combined performance of both cranes is equal to the sum of fractions and
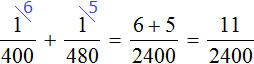
At the same time as the two taps are open, the plug is removed from the tub. Therefore, part of the water flowing into the bathtub immediately exits through the drain. This part will be expressed in fraction 
.
With each second the bath will be refilled by a certain fraction of water. Let's find out which part it is. To do this, subtract from the incoming part of the water the part that flows out through the drain.
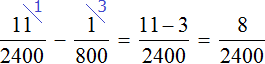
Let's find out how long it takes to fill the tub:
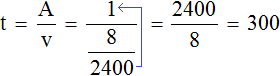
The bathtub will fill in 300 seconds. Since the task is complete, the seconds can be converted back to minutes. Three hundred seconds is five minutes:
300 : 60 = 5 min
Answer: The bathtub will fill in 5 minutes.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.