Let's look at some simple problems on topics we've already covered. For this, we will need a minimum of mathematical knowledge. In particular, be able to add, subtract, multiply and divide, find fractions from numbers, be able to calculate ratios, and perform elementary identity transformations.
The tasks in this lesson are easy enough to grasp and understand. It only takes a little skill to figure out which of the topics you have learned to use to solve the task at hand. Learning something is one thing, but applying it in practice is another.
Addition and subtraction tasks
Task 1. Five apples were placed in the fruit bowl and three more apples were placed in it. After some time two apples were taken from the cup. There are six apples left in the cup. Write an expression describing this movement of apples.
Solution
5 + 3 − 2 = 6
Task 2. 20 beds of carrots and 15 beds of beets were cultivated in the field. A total of 35 beds have been cultivated. Write the following expressions that contain addition and subtraction:
- An expression describing how many beds were cultivated in total. Place the total number of beds on the left side of the equation;
- An expression describing how five fewer beds of beets were tilled than carrots. Put the number responsible for the beets on the left side of the equation;
- An expression describing that the carrots have been tilled five more beds than the beets. Put the number for carrots on the left side of the equation;
Solution
35 = 20 + 15
15 = 20 − 5
20 = 15 + 5
Task 3. The car drove 980 km in three days. On Friday and Saturday it drove 725 km. How many kilometers did the car drive on each of these days, if it drove 123 kilometers more on Saturday than on Sunday?
Solution
Find out how many kilometers the car drove on Sunday. To do this, subtract the distance the car drove on Friday and Saturday (725 km) from the total distance (980 km)
980 − 725 = 255 km on Sunday
The condition says that the car drove 123 km more on Saturday than on Sunday. Therefore we must add 123 km to the distance the car drove on Sunday (255 km). So we get the distance the car traveled on Saturday
255 + 123 = 378 km on Saturday
Now find out how many kilometers the car drove on Friday. To do this, subtract from the total path (980) those paths the car drove on Saturday and Sunday. For convenience, these two paths can be added and the result subtracted from 980
980 − (378 + 255) = 980 − 633 = 347 km on Friday
Now let's check if the problem is solved correctly. To do this, add up all paths and see if the sum is equal to 980 km
347 + 378 + 255 = 980
980 = 980
Task 4: During three shifts the factory has produced 1680 meters of fabric. The first and second shifts together produced 970 meters of fabric, the second and third shifts produced 1060 meters. How many meters of fabric did each shift produce?
Solution
Let's find out how many meters of fabric produced by the first shift. To do this, subtract from the total number of meters that the second and third shifts made (1060m)
1680 − 1060 = 620m (the first shift produced)
Let's find out how many meters of fabric produced by the third shift. To do this, subtract from the total number of meters that the first and second shifts made (970m)
1680 − 970 = 710m (the third shift produced)
Let's find out how many meters of fabric were produced by the second shift. To do this, subtract from the total number of meters that the first and third shifts made (620m and 710m). For convenience, these two quantities can be added and the result subtracted from 1680
1680 − (620 + 710) = 1680 − 1330 = 350m (the second shift produced)
Let's check if the problem is solved correctly. To do this, add all quantities and see if the sum is equal to 1680m
620 + 350 + 710 = 1680
1680 = 1680
Task 5. There is the following equality
5 + 5 + 2 = 8 + 4
Both parts of the equality (both left and right) are equal to 12. Add 3 to the left side of the equation
5 + 5 + 2 + 3 ≠ 8 + 4
The equality is immediately broken. The left side is not equal to the right side, because the left side is now 15 and the right side is now 12. To keep the equality, add 3 to the right side of the equation
5 + 5 + 2 + 3 = 8 + 4 + 3
The sign "unequal" has disappeared. Now add one to the number 4, which is located on the right side of the equality
5 + 5 + 2 + 3 ≠ 8 + (4 + 1) + 3
The equality is broken again. The left side is not equal to the right side, because the right side is now 16, and the left side is 15.
Let's try again to "restore equality" between the left and right parts. To do this, you can add one to the left part. But you can also subtract one from any number on the right side. Let's leave the left part untouched and subtract one from the number 8, which is in the right part:
5 + 5 + 2 + 3 = (8 − 1) + (4 + 1) + 3
Task 6. By how many units is the number 78 greater than the number 63?
Solution
Subtract the number 63 from 78
78 − 63 = 15
78 is greater than 63 by 15 units.
Task 7. By how many units the number 88 is less than the number 105
Solution
Subtract the number 88 from 105
105 − 88 = 17
88 is 17 less than 105
Task 8: How much higher is the number 65 than the number 48 and lower than the number 95
Solution
Subtract 48 from 65
65 − 48 = 17
Subtract 65 from 95
95 − 65 = 30
65 is greater than 48 by 17 units, and less than 95 by 30 units.
Multiplication and division tasks
Task 1. 90 cups were equally placed in three boxes. The result is that each box contains 30 cups. Write an expression that describes that 90 cups are put into three boxes. Then perform the action in the expression.
Solution
90 : 3
90 : 3 = 30
30 = 30
Task 2. 60 plates were packed in boxes, six plates each. The result is 10 boxes. Write an expression that describes that 60 plates are put into boxes of 6 plates each. Then perform the action in the expression.
Solution
60 : 6
60 : 6 = 10
10 = 10
Task 3. There are 10 boxes of plates. There are 6 plates in each one. If you unpack all the boxes, you get 60 plates. Write an expression that describes that packing all the boxes results in 60 plates.
Solution
6 × 10 = 60 plates
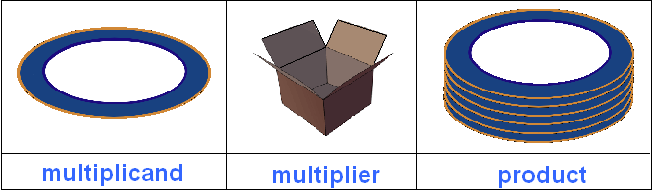
A small note should be made here. When constructing an expression containing a product, it is desirable to understand beforehand what is a multiplicand and what is a multiplier. By tradition, first write down the multiplicand and then the multiplier.
For example, if you want to increase the number 2 by three times, you should write 2 × 3. In this expression, the multiplicand is number 2, and the multiplier is number 3.
In the problem statement it was said that after unpacking there are 60 plates. So the final goal is to get these 60 plates. And they can be obtained by increasing the six plates tenfold. That is, multiplying 6 by a factor of 10. So the multiplicand is the plates, and the multiplier is the boxes. As a result, we will get plates, the number of which will be increased tenfold from the original.
Do not assume that the figure represents all 60 plates. This is just a model describing that multiplication results in plates, not boxes.
Of course, the product does not change by rearranging the places of the factors, but if you put number 10 in the first place and number 6 in the second place, you get the expression 10 × 6. In this expression, the multiplicand is the boxes and the multiplier is the plates. Then the result is not 60 plates, but 60 boxes, which violates the logic of the task:

As with the previous figure, do not think that it represents all 60 boxes resulting from multiplication. This is just a model describing that multiplication results in boxes, not plates.
As it was said above, the product does not change from the rearrangement of the places of the factors, and we can write the factors in any order, since the answer to the task will not change. Nevertheless, keeping track of the order of the factors allows us to understand the task and its essence.
The tradition of writing the multiplicand first, has survived only in some countries. In most other countries, they write the multiplier first and then the multiplicand. And this is more correct from the point of view of real mathematics.
For example, if we encounter the notation 5 cm, we read "five centimeters," not "centimeters five". Five in this case is a multiplier - a number by which one centimeter is increased fivefold. By "cm" we mean one centimeter:
5 cm = 5 × 1 cm
In everyday communication we often use product, sometimes without noticing it. And we pronounce first the multiplier and then the multiplicand. Examples: "five candies", "one hundred dollars", "ten tulips". We don't say "candies five", "dollars one hundred" or "tulips ten".
Recall the lesson "Algebraic expressions". This lesson was a basic lesson for the study of algebra. In it, we touched on the concept of a coefficient, a multiplier in front of a variable. We wrote this factor before the variable, for example 3a, 2x, 7y. We did not write a3, x2, y7. The first notation is more correct, and it is neater and more beautiful in terms of aesthetics. Later, when you study algebra and higher mathematics, you will more often notice that the multiplier comes first.
Task 4. There are 18 sheets in a notebook. How many notebooks can be made from 54 sheets?
Solution
18 sheets are one notebook. To find out how many of these notebooks can be made from 54 sheets, you need to group these 54 sheets by 18 sheets. To do this, divide 54 by 18. This allows you to find out how many notebooks can be made of 54 sheets:
54 : 18 = 3 notebooks
Task 5. In total (together) there are 72 sheets in several identical notebooks. Each notebook has 18 sheets. Write an expression to find out how many notebooks there are in total.
Solution
If there are 18 sheets in one notebook, then in order to know how many of the same 18 sheets (whole notebooks) there are in 72 sheets, divide 72 by 18
72 : 18 = 4 (notebooks)
Task 6. There are 75 sheets in three identical notebooks in total (together). How many sheets are in one notebook?
Solution
The notebooks are all the same. If we divide 75 by the number of notebooks, that is, by 3, we find out how many sheets there are per notebook:
75 : 3 = 25 sheets
Task 7. The father is 46 years old and the son is 23 years old. The father is twice as old as his son. Write an expression that describes that the father is twice as old as the son.
Solution
We write down the father's age and through the equal sign we write that the father's age is twice the age of the son:
46 = 23 × 2
Let's perform the action in the right part of the equality to make sure that the expression is correct - the equal sign should justify its position:
46 = 23 × 2
46 = 46
Task 8. A mother is 36 years old and her daughter is 12 years old. The daughter is three times younger than her mother. Write an expression describing that the daughter is three times younger than her mother.
Solution
Write down the daughter's age and through the equal sign write that she is three times younger than her mother
12 = 36 : 3
Perform the action on the right side of the equality - we get an identity:
12 = 12
Determine cost, length, mass, time, speed
Task 1. Nine books cost $162. How much are five of this books worth?
To solve similar problems, you first need to determine the cost of one unit of an item. Then use multiplication and determine the cost of several units of goods. In this case, $162 should be divided equally by nine books. That's how much one book is worth:
162 : 9 = $18.
We got the cost of one unit of goods. That is, the cost of one book is $18. Then, to find the value of five similar books, multiply 18 by the multiplier 5.
18 × 5 = $90.
Task 2. Eight magazines cost $176. Determine how many magazines you can buy for $66.
Let's determine the cost per magazine. To do this, divide the total price of $176 by eight magazines:
176 : 8 = $22.
22 dollars - the cost of one magazine. Let's determine how many magazines can be bought for $66. To do this, find out how many times $66 contains $22. In other words, divide $66 by the cost of one magazine:
66 : 22 = 3 magazines.
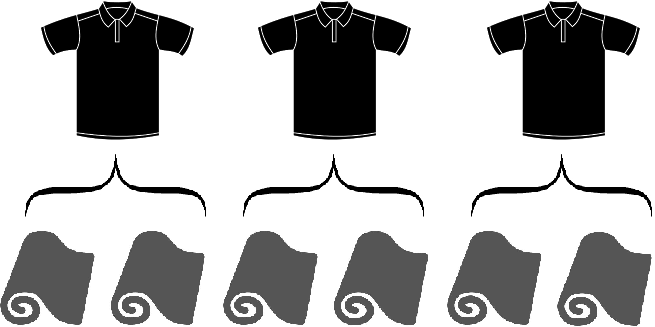
Task 3. Three shirts were made from six rolls of fabric. Determine how many rolls were used for one shirt
Solution
To determine how many rolls went for one shirt, divide 6 rolls by the number of shirts sewn, that is, by 3.
6 : 3 = 2
Task 4. 5 curtains were made from 15 meters of fabric. Determine how many curtains can be sewn from 42 meters of fabric.
Solution
Let's find out how many meters of fabric it takes to sew one curtain. To do this, divide 15 meters by the number of curtains sewn, that is, by 5
15 : 5 = 3 meters
It takes three meters to sew one curtain. To find out how many curtains can be sewn from 42 meters of fabric, you need to divide these 42 meters by 3 meters
42 : 3 = 14 curtains
Task 5. 6 loaves of bread were baked from 3 kg of flour. Determine how many loaves can be baked from 30 kg of flour.
Solution
Let's find out how many kilograms of flour it takes to make one loaf of bread. To do this, divide 3 kilograms by 6 loaves
3 : 6 = 0.5 kg per loaf
One bun takes 0.5 kg of flour. Let's find out how many loaves can be obtained from 30 kg of flour. To do this, divide 30 kg by 0.5
30 : 0.5 = 60 loaves
Task 6. Five identical bags of potatoes were bought with a total mass of 15 kg. Determine the mass of one bag
Solution
15 : 5 = 3 kg
Task 7. Father bought five identical bags of potatoes with a total weight of 20 kg. The son helped his father carry 2 bags. How many kilos of potatoes did the son carry?
Solution
Weight of one bag:
20 kg : 5 = 4 kg
The weight of the bags carried by the son:
4 kg × 2 = 8 kg.
Task 8. The speed of the helicopter is 250 km/h, and the speed of the airplane is 4 times greater. Determine the speed of the plane.
Solution
If the speed of the airplane is 4 times the speed of the helicopter, it is enough to multiply the speed of the helicopter by 4. So we get the speed of the airplane:
250 km/h × 4 = 1000 km/h.
Task 9. The train traveled 390 km in 6 hours, each hour equally. Determine how many kilometers this train traveled in 1 hour.
Solution
To determine how many kilometers the train traveled in one hour, it is sufficient to divide 390 by 6, i.e. to divide equally the distance by the time spent:
390 km : 6 = 65 km every hour
Task 10. A bouquet of flowers costs $25. What is the greatest number of bouquets you can buy for $160?
Solution
Divide 160 by 25
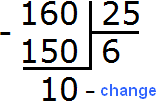
For 160 dollars you can buy a maximum of 6 bouquets, and still have change of 10 dollars.
Graphic representation of the task
It is useful to describe some tasks graphically in the form of diagrams, drawings, or tables. This allows you to find a solution faster and understand the essence of the task. There are also tasks that are difficult to solve if there is no graphical representation in front of your eyes.
Graphical description of the task is a creative process and here it all depends on your imagination.
Let's solve some simple tasks that can be described with the help of drawings.
Task 1. The factory had two pieces of fabric that were 96 meters long and 84 meters long each. They were used to make a coat. The second piece made 3 coats less than the first one. How many coats were made from each piece?
Solution
First, we need to know how many meters of fabric are used for one coat. Once we know this number, we will be able to divide by this number 96 meters and 84 meters, and thus know how many coats are made from each piece. But how do we do that?
Let's find out how much more 96 meters are than 84 meters. To do this, subtract 84 from 96.
96 m - 84 m = 12 m
96 meters is more than 84 meters by 12 meters. The task statement says that the second piece yielded three fewer coats than the first piece. This means that the first piece, on the contrary, made three more coats than the second one. For these three coats come the 12 meters of fabric we found. If we divide 12 meters by these 3 coats, we will find out how many meters of fabric are used for one coat:
12 : 3 = 4 meters per coat
Now you can find out how many coats are made from each piece of fabric. For this we divide the numbers 96 and 84 into 4 metres in turn
96 : 4 = 24 coats from the first piece
84 : 4 = 21 coats from the second piece.
We can check if the second piece really produced three fewer coats than the first one. Let's subtract 21 from 24
24 − 21 = 3
This task can be graphically represented. Let's represent 96 meters and 84 meters as two lines - the second one is shorter than the first one:

Draw a red line on top of these two lines so that this line crosses 96 meters on the section where the 84 meters end:
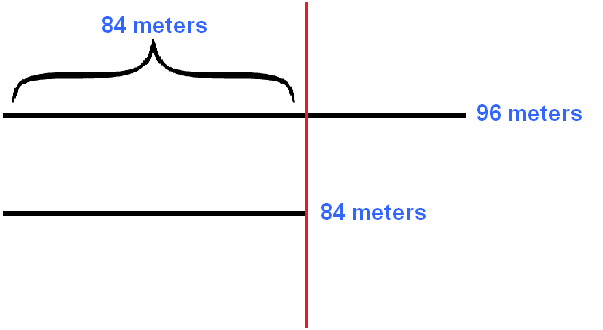
Now on the first piece of fabric after the red line we will draw three coats. After all, the first piece of fabric made three more coats:
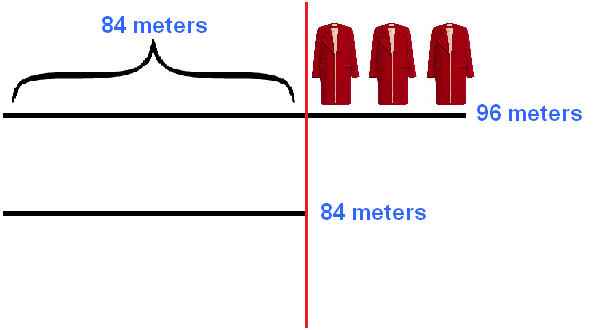
Well, then, if you look closely at the figure, you can understand what you need to do. The remainder of the first fabric (after the red line) should be equally divided by 3 coats and thus get the number of meters consumed per coat. The remainder of the first matter (after the red line) can be found by subtracting 84 meters from 96 meters.
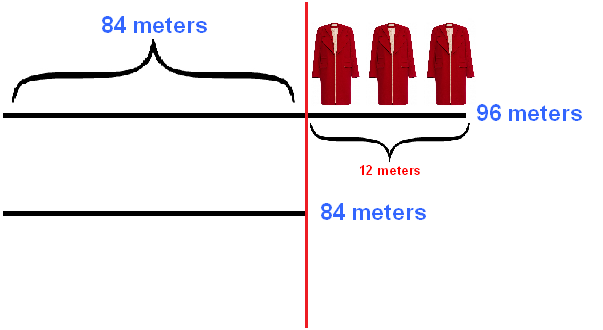
Now it is much more convenient to solve the problem. Divide 12 meters by three coats and determine how many meters of fabric are used for one coat.
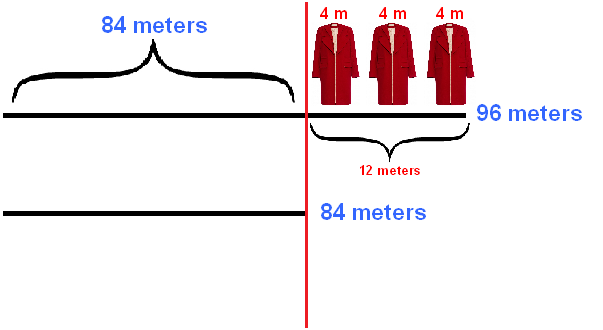
Then both pieces of fabric are divided by 4 and determine how many coats are sewn from each piece.
Task 2. In 4 hours the ship has traveled 136 km. How many kilometers will it cover in 8 hours if it moves at the same speed?
Solution
Let's find the speed of the motor ship. Recall that speed is the distance traveled by a body (person, car, boat) in 1 hour, 1 minute or 1 second. To find the speed, divide the distance traveled by the time of travel:
136 : 4 = 34 km/h
So the ship travels 34 kilometers in one hour. The problem says that the ship moves at the same speed. This allows us to find out how many of these 34 kilometers the ship travels eight times (in 8 hours)
34 km × 8 = 272 km
You can also make a drawing for this problem. It would be especially useful if you can't remember what speed is.
Let's draw 136 kilometers as a line:
![]()
Above this line we draw four lines that will represent four hours. They in turn will tell us how many kilometers the ship travels in an hour
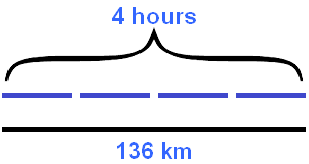
Since the speed of the ship is the same in each hour, we can add another 4 hours, thereby making a clue to ourselves with the distance traveled:
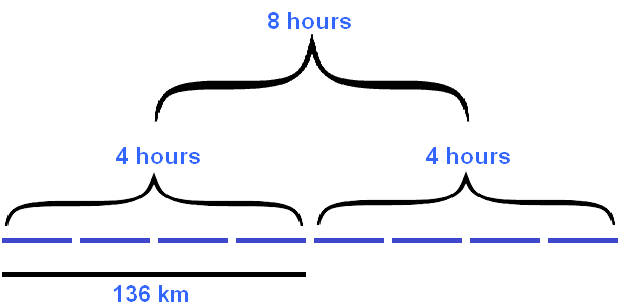
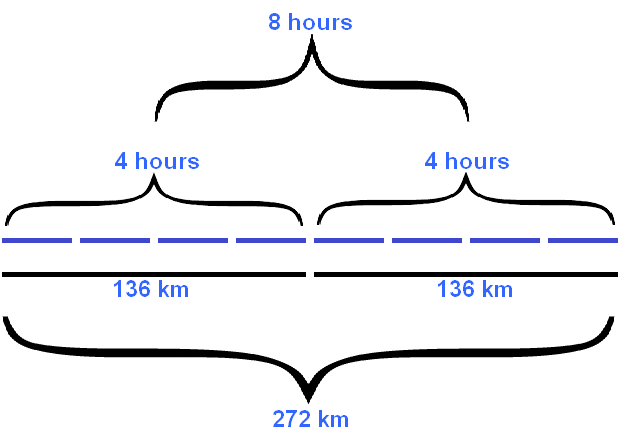
A close look at the figure reveals that the distance has doubled. We can write down the product 136×2 equal to 272 kilometers. We can also draw the bottom line representing the distance traveled:
136 × 2 = 272 km
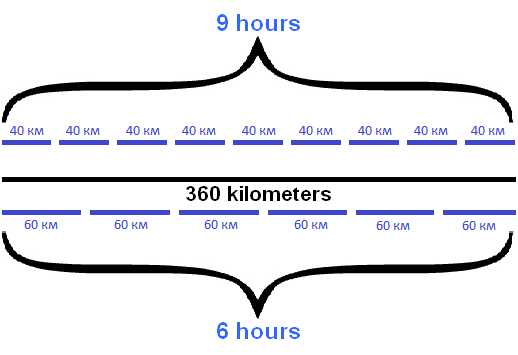
Task 3. The freight train traveled from one station to another in 9 hours, and the passenger train in 6 hours. What is the speed of the passenger train if the speed of the freight train is 40 km/h?
Solution
The question of the problem is to find the speed of a passenger train. To find the speed of the passenger train, we need to divide the distance traveled by the time of its movement. But the thing is that we do not know the distance traveled. All we know is its travel time - 6 hours.
But the task has a hint that the freight train travelled the same distance in 9 hours and its speed was 40 km/h. This allows us to know the distance between the stations. If the freight train travels 40 kilometers in one hour, then it traveled nine times more in 9 hours:
40 km × 9 = 360 km.
Now we know the distance between the stations. It is equal to 360 kilometers. This makes it easy to find the speed of the passenger train. Recall that to do this you need to divide the distance traveled (360 km) by the travel time of the passenger train (6h)
360 : 6 = 60 km/h
Draw a diagram for this problem. First, we represent the time of a freight train in the form of nine lines. The same lines will represent how many kilometers the freight train travels in an hour:
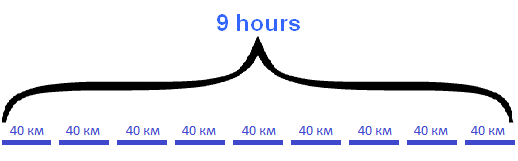
Below these lines, draw a solid line that represents the distance traveled by this train

Below from the solid line depicting the distance, draw six lines that represent the travel time of the passenger train:
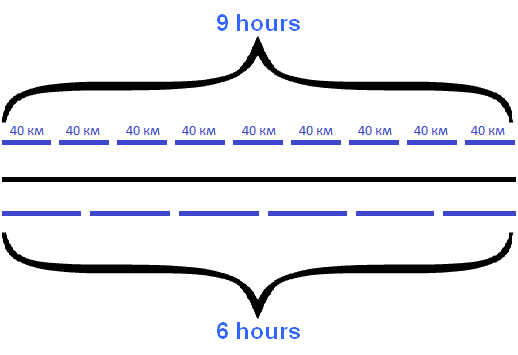
If you look carefully at the resulting figure, you can understand what to do next. You can add up all the distances traveled by the freight train during nine hours of movement (40 km in each hour) and get the length of the entire route. Then divide the resulting distance by the travel time of the passenger train (6 hours) and get the speed of its movement.
Task 4. A boarding school with 250 childrens has a stock of 22500 kg of potatoes for 180 days. How many days' supply of potatoes is made in another boarding school, if the same norm for 160 childrens is 9600 kg of potatoes?
Solution
First let's deal with the first school. It has 250 childrens. There are 22500 kg of potatoes for them for 180 days. Let's make a picture of the problem in the form of a table. Tables are another useful way that allows you to organize the data in a task and find its solution faster
| Distribution of potatoes per 250 children | |
| 22500 kg | for 180 days |
| ? | for 1 day |
Determine how many kilograms of potatoes per day. To do this, divide 22500 kg by 180 days
22500 kg : 180 days = 125 kg per day
Let's add a new value to our table. Instead of the question mark, insert the found 125 kilograms, which comes to one day
| Distribution of potatoes per 250 children | |
| 22500 kg | for 180 days |
| 125 kg | for 1 day |
So, 250 childrens are given 125 kilograms of potatoes a day.
Let's determine how many kilograms of potatoes per day per children. To do this, divide 125 kilograms by 250 children
| Distribution of potatoes per 250 children and 1 child per day |
|
| 125 kg | for 250 children |
| ? | for 1 child |
125 kg : 250 p = 0.5 kg per day per children
Let's add a new value to our table. Instead of the question mark, let's insert the found 0.5 kilograms per child per day
| Distribution of potatoes per 250 children and 1 child per day |
|
| 125 kg | for 250 children |
| 0.5 kg | for 1 child |
So, 0.5 kg is the mass of potatoes allocated per children per day. The same mass is the norm of potatoes per children per day
| Norm of potatoes per child per day | |
| 0.5 kg | for 1 day |
The task says that the second school at the same rate allocated 9600 kilograms of potatoes for 160 childrens. If we multiply 0.5 kilograms of potatoes by 160 childrens, we find out how many kilograms of potatoes per 160 childrens per day
0.5 kg × 160 c = 80 kg of potatoes for 160 children
And if we divide 9600 kilograms by 80 kilograms, we will find out how many days the allocated potatoes at the second school will be enough. That is, we get the answer to the problem by finding out how many days of the potato reserve at the second boarding school
9600 kg : 80 kg = 120 days
| Distribution of potatoes for 160 children | |
| 80 kg | for 1 day |
| 9600 kg | for 120 days |
Finding GCD and LCM
Task 1. There are 42 candies. Write the following expressions containing division:
- An expression in which 42 candies are divided into 2 children;
- An expression in which 42 candies are divided into 3 children;
- An expression in which 42 candies are divided into 7 children;
- An expression in which 42 candies are divided into 14 children;
- An expression in which 42 candies are divided into 21 children;
- An expression in which 42 candies are divided into 42 children;
Solution
- 42 : 2 = 21
- 42 : 3 = 14
- 42 : 7 = 6
- 42 : 14 = 3
- 42 : 21 = 2
- 42 : 42 = 1
Task 2. There are three children playing outside. We have 24 Snickers candy bars and 18 Twix candy bars. We need to distribute these chocolates to the children so that everyone gets an equal share.
Solution
First, divide 24 Snickers candies among three children:
24 : 3 = 8 (each child gets one Snickers bar).
Then we divide 18 Twix chocolates by the same three children:
18 : 3 = 6 (Twix chocolates for each child).
Each child receives 8 Snickers and 6 Twix.
Task 3. There are 24 Snickers candy bars and 18 Twix candy bars. What is the greatest number of identical gifts that can be made from these candy bars?
Solution
This task is similar to the previous one. In the previous one, we divided these candy bars among the three children. But these candy bars could be divided not only among three children, but also among two, four, or six.
In this case, the question is to determine the largest number of children on whom to divide the candy bars. At the same time, divide them so that each child gets an equal share of the candy bars and so that we have nothing left.
In such cases, you need to find the greatest common divisor (GCD) of two numbers - in our case, 24 and 18. Recall that GCD is the greatest number by which both numbers are divided without a remainder. And this is what we need.
Find the GCD of numbers 24 and 18
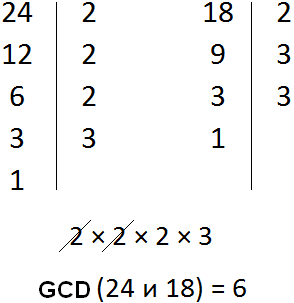
So there are 24 Snickers candy bars and 18 Twix candy bars to make six identical gifts.
We can scatter (divide) each kind of candy bars into six gifts and find out how many candy bars of each kind will be in each gift:
24 : 6 = 4 (Snickers candy bars)
18 : 6 = 3 (Twix candy bars)
Each gift contains 4 Snickers candy bars and 3 Twix candy bars.
Task 4. There are 60 apples and 40 pears. What is the greatest number of children that can be equally given these fruits? How many apples and pears will each child get?
Solution
The children in this case are the greatest common divisor. Our task is to find this GCD in order to distribute 60 apples and 40 pears equally.
The greatest common divisor of 60 and 40 is 20. So 60 apples and 40 pears can be equally distributed to 20 children.
Let's distribute 60 apples:
60 : 20 = 3 (apples to each child).
Let's distribute 40 pears:
40 : 20 = 2 (pears to each child)
Each child received three apples and two pears.
Task 5. The fabric material is sold by 3 meters or by 4 meters. What is the smallest number of meters that should be in a roll so that the material can be sold without any leftovers?
Solution
In order to sell the material without a remainder, the number of its meters must be divisible by 3 and by 4 meters without a remainder. We know that the number that is divisible by both numbers without a remainder is called the lowest common multiple of those numbers. This is the case in this problem. To answer the question we need to find the LCM of numbers 3 and 4.
The LCM of numbers 3 and 4 is 12. So the smallest number of meters of material must be 12, so it can be sold without a remainder.
Task 6. A small box holds 24 pencils, and a large box holds 30 pencils. Determine the smallest number of pencils that can be placed in both small and large boxes.
Solution
The least common multiple of 24 and 30 is 120. So 120 pencils can be placed in both small and large boxes.
In case we put 120 pencils into small boxes, we will need 5 small boxes:
120 : 24 = 5
In case we put 120 pencils in big boxes, we need 4 big boxes:
120 : 30 = 4
Conversion of units of measurement
Task 1. Convert three minutes in seconds.
There are 60 seconds in one minute and 180 seconds in three minutes:
60 × 3 = 180 (seconds)
3 minutes = 180 seconds
Task 2. Convert ten minutes in seconds.
There are 60 seconds in one minute and 600 seconds in ten minutes:
60 × 10 = 600 (seconds)
10 minutes = 600 seconds
Task 3. Convert eight minutes in seconds.
There are 60 seconds in one minute and 480 seconds in eight minutes:
60 × 8 = 480 (seconds)
8 minutes = 480 seconds
Task 4. Convert 2 minutes and 3 seconds in seconds.
Two minutes is 120 seconds plus 3 seconds, which do not need to be translated anywhere:
60 × 2 = 120
120 + 3 = 123 (seconds)
2 min 3 s = 123 s
Task 5. Convert 15 minutes and 47 seconds in seconds.
15 minutes is 900 seconds plus 47 seconds, which do not need to be translated anywhere:
60 × 15 = 900 seconds
900 + 47 = 947 seconds
15 min 47 s = 947 s
Task 6. Convert 3 centners and 45 kilograms in kilograms.
First, convert 3 centners to kilograms. One centner is 100 kilograms, and three centners is 300 kilograms. Plus we have another 45 kilograms. So we have to add 300 and 45. The result is 345 kilograms:
3c 45 kg = 300 kg + 45 kg = 345 kg
Task 7. Convert 4 kilograms and 654 grams in grams
First, let's convert 4 kilograms to grams. 1 kilogram is 1000 grams, and 4 kilograms is 4000 grams. Plus we have another 654 grams. So we have to add 4000 and 654. We end up with 4654 grams:
4 kg 654 g = 4000 g + 654 g = 4654 g
Task 8. Convert 20 seconds in minutes. Write the answer as a fraction:
20 sec. = ![]() min
min
The expression ![]() means that the minute is divided into 60 equal parts (into 60 seconds), and 20 parts are taken from those parts.
means that the minute is divided into 60 equal parts (into 60 seconds), and 20 parts are taken from those parts.
Task 9. Convert 15 seconds in minutes. Write the answer as a fraction:
![]()
Task 10. Convert 45 minutes in hours. Write the answer as a fraction:
45 min = ![]() h.
h.
The expression ![]() means that an hour is divided into 60 parts, and 45 parts are taken from those 60 parts. And the 45 parts of 60 are 45 minutes.
means that an hour is divided into 60 parts, and 45 parts are taken from those 60 parts. And the 45 parts of 60 are 45 minutes.
Task 11. The mass of a horse is 500 kg. Express this mass in tons. Write the answer as an ordinary fraction:
![]()
Task 12. Write 6 minutes and 15 seconds as a mixed number
Six minutes is an integer part of a mixed number. Fifteen seconds is fifteen seconds out of sixty seconds, so ![]() is the fractional part
is the fractional part
6 min. 15 sec. = 6![]()
Task 13. Write 43 meters and 5 centimeters as a mixed number
43 meters is an integer part of a mixed number. Five centimeters is five centimeters out of a hundred centimeters, so ![]() would be the fractional part of a mixed number:
would be the fractional part of a mixed number:
43 m 5 cm = 43![]() m.
m.
Task 14. To 6 centners of 87 kg add 2 center of 45 kg
Let's write the task as an expression:
6 c 87 kg + 2 c 45 kg
For convenience, let's convert these values into kilograms, we get 687 kg and 245 kg. Let's add these kilograms and get 932 kg. Then let's break down the centners and the rest of the kilograms separately:
6 c 87 kg + 2 c 45 kg = 687 kg + 245 kg = 932 kg = 9 c 32 kg
The second way is with mixed numbers:
![]()
Task 15. Find the value of the following expression: 3 kg 6 g - 2 kg 3 g
Solution
3 kg 6 g - 2 kg 3 g = 30006 g - 2003 g = 1003 g = 1 kg 3 g
Let's solve this task with mixed numbers:
![]()
Thus, subtracting two from three yielded one, which became the integer part of the resulting mixed number. The value of the expression ![]() became a fraction
became a fraction ![]() , which became the fractional part of the mixed number.
, which became the fractional part of the mixed number.
But the expression ![]() could have been calculated by converting the mixed numbers into improper fractions. The solution would look like this:
could have been calculated by converting the mixed numbers into improper fractions. The solution would look like this:
![]()
Of course this solution looks more cumbersome than the first solution. The first one looks much shorter and neater:
![]()
But keep in mind that in solving such tasks it sometimes happens that the fractional part of the minuend is smaller than the fractional part of the subtrahend. In this case, it is advisable to look for workarounds to make the solution shorter. Otherwise, the task may take up half a page.
Task 16. Find the value of the following expression:
43 m 5 cm - 37 m 86 cm
Solution
43 m 5 cm - 37 m 86 cm = 4305 cm - 3786 cm = 519 cm = 5 m 19 cm
Now let's try to solve this task with mixed numbers
![]()
We see that the fractional part of the minuend is smaller than the fractional part of the subtrahend. If we try to calculate the integer and fractional parts separately, we get a rather cumbersome solution:
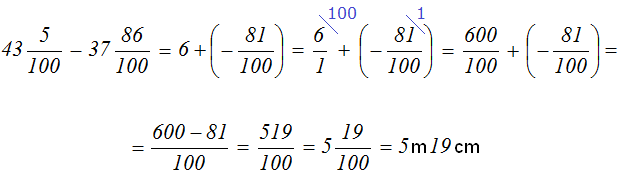
And if you first convert the mixed numbers to improper fractions, you can write down the solution much shorter:
![]()
You can also use another method, which is often used in schools. The essence of the method is that they take one unit off the integer part of the minuend, and present it as a fraction with the same denominator as the fractional part of the minuend. This fraction is then added to the fractional part of the minuend.
Let's write the minuend ![]() in the following form:
in the following form:
![]()
We removed one from the integer part of 43 - the integer part is now the sum of the numbers 42 and 1. Now represent the unit as a fraction with the same denominator as the fraction ![]()
![]()
Now add the fractions ![]() and
and ![]() - we get the following expression:
- we get the following expression:
![]()
The minuend that used to be ![]() is now
is now ![]() . We see that the problem of the minuend has disappeared - it is larger than the subtrahend. This allows us to calculate the integers and fractions separately and get a short solution:
. We see that the problem of the minuend has disappeared - it is larger than the subtrahend. This allows us to calculate the integers and fractions separately and get a short solution:
![]()
When solving such simple tasks, you don't have to resort to fractions, much less to such methods as we're discussing now. Your goal is to be able to apply your knowledge in practice.
Task 17. Find the value of the following expression:
24 c 6 kg - 21 c 78 kg
Solution
24 c 6 kg - 21 c 78 kg = 2406 kg - 2178 kg = 228 kg = 2 c 28 kg
Task 18. Find the value of the following expression:
16 km 34 m - 8 km 546 m
Solution
16 km 34 m - 8 km 546 m = 16034 m - 8546 m = 7488 m = 7 km 488 m
Task 19. Perform addition:
15 h 28 min + 6 h 37 min
Solution
15 h 28 min + 6 h 37 min = 928 min + 397 min = 1325 min
We got 1325 minutes. Express this answer in hours and minutes. To do this, we "take out" the hours from 1325.
60 minutes is one hour. And to understand how many such 60 minutes (hours) are contained in 1325 minutes, we must divide 1325 by 60
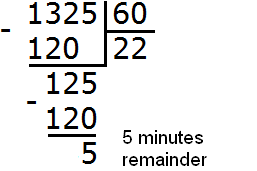
We get the answer that 1325 minutes is 22 hours and 5 minutes
15 h 28 min + 6 h 37 min = 928 min + 397 min = 1325 min = 22 h 5 min
Task 18. The world's first Soviet artificial satellite had a mass of 83 kg 600 g. The mass of the second satellite was 424 kg 700 g more than the mass of the first satellite and 818 kg 700 g less than the mass of the third satellite. Determine the mass of the third artificial earth satellite.
Solution
Let's find the mass of the second satellite. It is greater than the mass of the first satellite by 424 kg 700 grams. Let's add another 424 kg and 700 grams to the mass of the first satellite
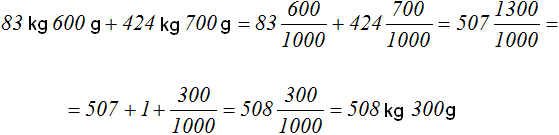
Further, it is said that the mass of the second satellite is less by 818 kg and 700 grams. If we add 818 kg and 700 grams to the mass of the second satellite, we get the mass of the third satellite
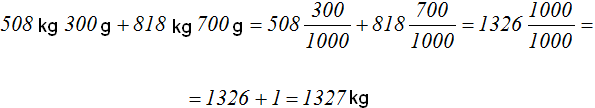
So the third artificial satellite has a mass of 1327 kilograms.
Exercises
Solution
Let's determine how many buckets of water were in the two barrels originally. To do this, add the remaining water in both barrels (34) and (20) plus the 16 buckets that were taken from them:
34 + 20 + 16 = 70 buckets of water were originally in both barrels.
Since the barrels are the same, we can divide 70 by 2 and find out how many buckets were in each barrel individually:
70 : 2 = 35 buckets in each barrel.
The first barrel had 34 buckets left. Subtract 34 buckets from 35 buckets, and find out how many buckets were taken from the first barrel:
35 - 34 = 1 bucket taken from the first barrel
There are 20 buckets left in the second barrel. Subtract 20 buckets from 35 buckets - find out how many buckets were taken from the second barrel:
35 - 20 = 15 buckets taken from the second barrel</em
The problem condition says that one bucket holds 9 liters. Multiplying 9 liters by the number of buckets we took, we find how many liters of water were taken from each barrel.
9 × 1 = 9 liters of water taken from the first barrel
9 × 15 = 135 liters of water taken from the second barrel
An answer: from the first barrel they took 9 liters of water, from the second barrel 135 liters.
Solution
Determine how many seeds one wild radish plant produces per year. To do this, divide 180,000 by 15:
180,000 : 15 = 12,000 seeds per plant.
If one plant yields 12,000 seeds, then 80 plants will yield eighty times that amount. To find out exactly how many, multiply 12,000 by 80:
12,000 × 80 = 960,000 seeds will yield 80 plants
An answer: 80 wild radish plants will yield 960,000 seeds.
Solution
Determine how many dollars were paid for the apples. To do this, multiply 0.6 by the number of kilograms, i.e. 5:
0.6 × 5 = $3 apples.
Let's subtract that $3 from the total amount of money paid ($6.8). That's how we find out how many dollars were paid for sugar:
6.8 - 3 = $3.8 paid for sugar.
Let's find out how much a kilogram of sugar costs. To do this, divide $3.8 by the number of kilograms, that is, by 4
3.8 : 4 = $0.95 a kilo of sugar
An answer: 1 kilogram of sugar costs $0.95.
Solution
If we divide 3240 by the number of days (12, 15 and 20) one by one, we find out how many books each workshop can bind per day. Then you add up the results and find out how many books three workshops can bind at the same time per day. And if we divide 3,240 books by the number of books bound together in one day by three shops, we know how many days it takes them to complete the order simultaneously:
3240 : 12 = 270 (books) per day by 1 workshop
3240 : 15 = 216 (books) per day by 2 workshops
3240 : 20 = 162 (books) per day by 3 workshops
270 + 216 + 162 = 648 (books) per day by 3 workshops simultaneously
3240 : 648 = 5 (days) it will take the workshops to bind all the books.
An answer: 5 days are needed for the three shops to bind all the books.
Solution
Determine how much money Mom paid for 4.5 kg of cereal. To do this, multiply $12.8 × 4.5
12.8 × 4.5 = $57.6 paid for 4.5 kg of grits
Let's make the grits $3.2 more expensive:
12.8 + 3.2 = $16.
Let's find out how much groats we can buy for 57.6 rubles. To do this, we will divide 57.6 dollars by the price per kilogram, i.e. by 16
Divide the $57.6 by the price per kilogram.
57.6 : 16 = 3.6 kilograms
An answer: 3.6 kilograms of cereal at a price of $16 per kilogram can be bought for $57.6.
Decision
Determine how many hours each painter worked:
7 × 6 = 42 hours worked first painter
6 × 5 = 30 hours worked second painter
Determine how many hours the windows were painted:
42 + 30 = 72 hours total time of painting frames.
Determine how many frames are painted in 1 hour. To do this, divide the total number of painted frames (144) by the total time of their painting (72)
The total number of painted frames (144).
144 : 72 = 2 windows painted in one hour.
Determine how many frames the first painter painted:
2 × 42 = 84 windows painted by the first painter
Determine how many frames the second painter painted:
2 × 30 = 60 frames the second painter painted
An answer: the first painter painted 84 windows. The second painter painted 60 frames.
The solution
Determine the total number of boxes:
10 + 14 = 24 boxes
Determine how many units of bread per tray. To do this, divide the total number of units of bread (288) by the total number of boxes (24)
decide how many units of bread per tray
288 : 24 = 12 units of bread per tray.
The number of units of bread on the boxes is the same. Determine how many loaves of black bread were brought to the bread department:
12 × 10 = 120 loaves of black bread were brought to the department.
Determine how many loaves of white bread were brought to the bread department:
12 × 14 = 168 loaves of white bread were brought to the bread department.
Response: The bread department brought 120 loaves of black bread and 168 loaves of white bread.
Decision
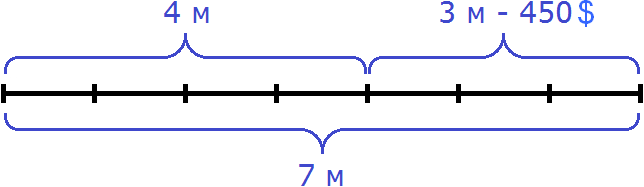
The difference between 7m and 4m is 3m. The $450 $ specified in the problem is for these 3 m. Let's determine how many dollars come to 1 m of silk. To do this, divide $450 $ by 3
450 : 3 = $150 - cost of 1 meter of silk.
An answer: the cost of 1 m of silk is $150
Decision
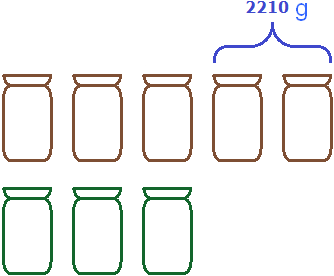
The difference between five cans and three cans is two cans. These two jars account for 2,210 grams. Let's determine how many grams are in one jar. To do this, divide 2210 g by 2
2210 : 2 = 1105 g is the mass of one jar.
Determine how much millet is in the cupboard. To do this, let's multiply 1105 g by the number of cans of millet:
1105 × 5 = 5525 grams of millet in the cupboard.
Determine how many peas are in the cupboard. To do this, multiply 1105 g by the number of jars of peas:
1105 × 3 = 3315 grams of peas in the cupboard.
An answer: there are 5525 g of millet and 3315 g of peas in the cupboard.
Solution
Determine how many kilograms of flour were obtained from 6,360 kg of wheat. To do this, we subtract 860 kg of waste from 6360 kg of wheat:
6360 - 860 = 5500 kg of flour was obtained.
Determine the number of bags in which the flour was poured:
28 + 32 + 40 = 100 bags.
Determine the mass of one sack. For this purpose let's divide 5500 kg of flour by the number of sacks:
5500 : 100 = 55 kg - mass of one bag.
Determine how many kilograms of flour were loaded on each machine:
55 × 28 = 1540 kg loaded on the first machine.
55 × 32 = 1760 kg loaded on the second machine.
55 × 40 = 2200 kg loaded on the third machine.
An answer: the first machine loaded 1,540 kg of flour, the second loaded 1,760 kg, and the third loaded 2,200 kg.
Large number abbreviations
Different abbreviations for large numbers are often given in the problems. Instead of zeros the abbreviations thousand million, billion are used.
Example 1. Instead of writing down 1000 the abbreviation 1 K is used.
Example 2. Instead of writing down 2000 the abbreviation 2 K is used.
Example 3. Instead of writing 1000000 the notation 1 M is used.
Example 4. Instead of writing 1000000000 we use the notation 1 B.
Abbreviations K, M, B replace the multipliers 1000, 1000000, 1000000000 respectively. To write a number in full without abbreviations, just multiply it by the appropriate multiplier.
For example, if the number in the letter is 5,500, you need to multiply it by 1000 to write it in full
5,5 × 1000 = 5500
Example 2. Write the number 1.5K without abbreviation
The abbreviation K points us to the multiplier 1000. Let's multiply 1500 by it
1500 × 1000 = 1 500 000
Example 3. Write the number 1500.5 K without abbreviation
1500,5 × 1000 = 1 500 500
Example 4. Write the number 11.2 K without abbreviation
11,2 × 1000 = 11 200
Example 5. Write 1.5 M without the abbreviation
The abbreviation million points us to the multiplier 1000000. Multiply 1.5
1,5 × 1000000 = 1500000
Example 6. The father's salary is $32.7 K and the mother's salary is $28.2 K. Write these numbers down without abbreviations.
32.7 × 1000 = $32700
28.2 × 1000 = $28,200
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.