Our first lesson was about numbers. We learned about a small part of this topic. In fact, it's much more complex. It has many rules and tricks.
Today we're going to continue studying numbers, but unfortunately, we're not going to cover all at once, so that we don't get tired with extra information that we don't really need at first. We're going to talk about Place value.
What is Place value?
Definition. Place value is the value of each digit in a number, every digit in a number has a place value.
Take the number 635 as an example.
This number consists of three digits: 6, 3 and 5.
The digits should be read from right to left. In the number 635, the first position has digit 5, the second position has digit 3, and the third position has digit 6.
The position where the number 5 is located represents ones
The position where the digit 3 is located represents tens
The position where the number 6 is located represents hundreds
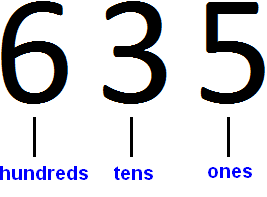
Each of us has heard such things as "ones," "tens," and "hundreds" since school. The digits indicate the position of the digit in the number and give us some information about the number itself. In particular, digits tell us how big a number is. Digits tell us how many ones, how many tens, and how many hundreds there are in a number.
Let's go back to number 635. There is a five in the ones. What does that tell us? It means that ones has five ones. It looks like this:
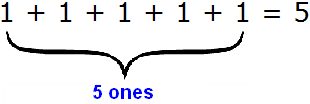
The digit of tens contains three 10. It looks like this:
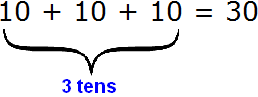
The digit of hundreds is 6. It looks like this:
If we sum up the number of ones, the number of tens, and the number of hundreds, we get our original number of 635
![]()
There are bigger numbers such as the thousands, ten thousands, hundred thousands, millions, and so on. We will rarely consider such big numbers, but it is nevertheless important to know about them as well.
For example, in the number 1 645 832 value place of ones contains 2 units, tens contains 3 tens, hundreds contains 8 hundreds, thousands contains 5 thousands, tens thousands contains 4 ten thousands, hundreds thousands contains 6 hundreds thousands, millions contains 1 million.
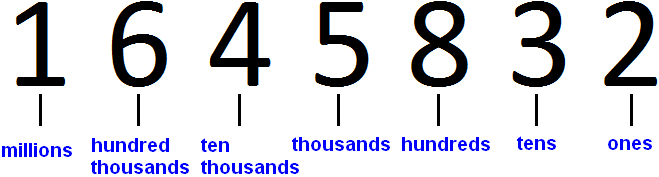
At the first time, while learning the digits, it is important to understand how many ones, tens, and hundreds a certain number contains. For example, number 9 contains nine ones. The number 12 contains two ones and one tens. The number 123 contains three ones, two tens and one hundred.
Grouping items
After counting some items, the ones, tens, thousands... can be used to group those items. For example, if we count 35 bricks in a yard, we can use the places to group those bricks. For example, the number 3 in the number 35 would say that the number 35 contains three tens. This means that 35 bricks can be grouped three times by ten.
So, let's group the bricks three times by ten pieces each:
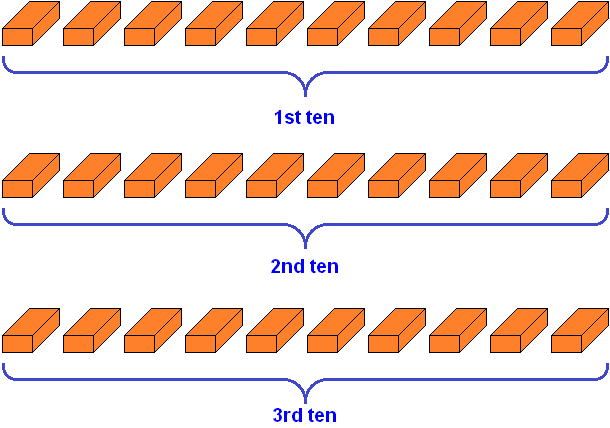
We got thirty bricks total. But there are five more bricks left. We'll call them "five ones".
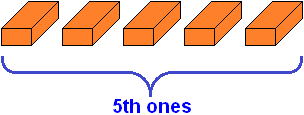
It turned out three tens and five ones of bricks - 35 total.
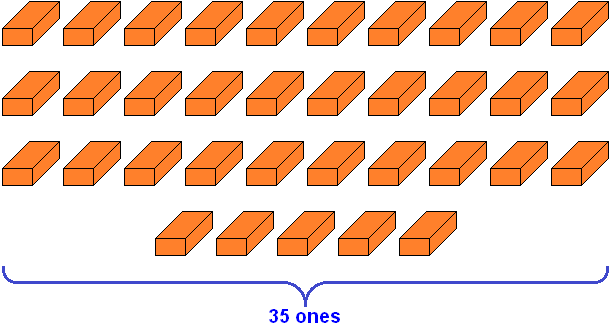
And if we did not group the bricks into tens and ones, we could say that the number 35 contains thirty-five ones. Such grouping would also be acceptable:
All numbers can be described in the same way. For example, the number 123. Earlier we said that this number contains three ones, two tens, and one hundred. But we can also say that this number contains 123 ones. Moreover, you can group this number in another way, saying that it contains 12 tens and three ones.
The words ones, tens, hundreds represent multipliers: 1, 10 and 100.
For example, the digit 3 is in the ones of 123. Using the multiplier 1, we can write that this unit is contained in the ones place value three times:
1 x 3 = 3
Next, in the tens of number 123, there is the digit 2. Using the multiplier 10, we can write something like this:
10 x 2 = 20
Next, the number 1 is in the hundreds of 123. Using the multiplier 100, we can write that there is only one hundred in 123:
100 x 1 = 100
If you add up 3, 20, and 100, you get the number 123
3 + 20 + 100 = 123
The same will happen if we say that the number 123 contains 12 tens and 3 ones. In other words, the tens will be grouped together 12 times:
10 x 12 = 120
And ones three times:
1 x 3 = 3
This can be understood from the following example. If there are 123 apples, you can group the first 120 apples 12 times by groups of 10 apples:

One hundred and twenty apples as a result. But there are three apples left. Let's call them "three ones".

If you add up the results of 120 and 3, you again get the number 123
120 + 3 = 123
You can also group 123 apples into one hundred, two tens, and three ones.
Let's group the hundred:

Let's group the two tens:
Let's group the three ones together:

If you add up 100, 20, and 3, you get 123 again.
100 + 20 + 3 = 123
Finally, consider the last possible grouping, where the apples will not be divided into tens and hundreds, but will be put together. In this case, the number 123 will be read as "one hundred and twenty-three ones". This grouping would also be possible:

1 x 123 = 123
Example 1. Read the number 523 in all possible ways.
The number 523 can be read as 3 ones, 2 tens, and 5 hundreds:
1 x 3 = 3 (three ones)
10 x 2 = 20 (two tens)
100 x 5 = 500 (five hundreds)
3 + 20 + 500 = 523
It can also be read as 3 ones of 52 tens:
1 x 3 = 3 (three ones)
10 x 52 = 520 (fifty two tens)
3 + 520 = 523
You can also read the number 523 as 523 units:
1 x 523 = 523 (five hundred and twenty-three units)
Where to use value places?
Value places make some calculations much easier. Imagine that you are solving a problem. You are almost done with the problem, all that is left is to calculate the last expression and get the answer. The expression to be calculated like this:
![]()
I don't have a calculator, but I want to write down the answer quickly and surprise everyone with the speed of my calculations. Everything is simple if you add up ones separately, tens separately, and hundreds separately. You need to start with the ones. First of all, you must mentally put three dots after the equal sign (=). Instead of these dots there will be digits of a new number (our result):
![]()
Now let's start to sum. The ones of 632 contains the number 2, and the ones of 264 contains the number 4. This means that the ones of 632 contains 2, and the ones of 264 contains 4. If we add up 2 and 4, we get 6. Write 6 in the ones of the new number (our result):
![]()
Next, we sum tens. The digit 3 is in the tens of 632, and the digit 6 is in the tens of 264. This means that the value place of tens of the number 632 contains three tens, and the value place of tens of the number 264 contains six tens. Add up 3 and 6 tens, and you have 9 tens. Write 9 in the tens value place of the new number (our result):
![]()
Finally, we add up hundreds separately. The hundred digit of 632 contains the digit 6, and the hundred digit of 264 contains the digit 2. This means that the hundreds of 632 contains six hundreds, and the hundreds of 264 contains two hundreds. Add 6 and 2 hundreds, and you get 8 hundreds. Write the number 8 in the hundreds of the new number (our result):
![]()
Thus, if you add 264 to the number 632, you get 896. Of course, you will calculate an expression like that faster and people around you will begin to wonder about your skills. They'll think you're calculating big numbers quickly, when in fact you were calculating small numbers. You may agree that calculating small numbers is much easier than calculating big numbers.
Place value overflow
A digit is characterized by a single number from 0 to 9. But sometimes a place value overflow may occur when calculating a numerical expression in the middle of a solution.
For example, adding the numbers 32 and 14 does not cause an overflow. Adding the units of these numbers will give 6 units in the new number. Adding the tens of these numbers will add 4 tens to the new number. The answer is 46 or six ones and four tens.
![]()
But when you add 29 and 13, there will be an overflow. Adding the ones of these numbers gives 12 ones, and adding the tens gives 3 tens. You cannot write 12 ones in one value place by one digit:
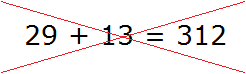
The value of 29 + 13 is 42, not 312. What should we do in case of an overflow? In our case, the overflow happened in the ones value place of the new number. When you add nine and three ones, you get 12 ones. Only digits in the range from 0 to 9 can be written in the ones/tens/etc.
The point is that twelve ones is not just "twelve ones". Another way to read this number is "two ones and one ten". The ones digit is for ones only. Tens have no place there. Adding 9 ones and 3 ones gives us 12 ones, which should be called two ones and one tens. By writing two ones and one tens in one digit, we've made a mistake, which eventually led to the wrong answer.
To correct this, write two ones in the ones place value of the new number, and transfer the remaining tens to the next digit of tens. After adding the tens in the example 29 + 13, we will add to the result the tens that remained when adding the ones.
So, 2 of the 12 ones we should write in the ones place value of the new number, and one tens we should move to the next value place
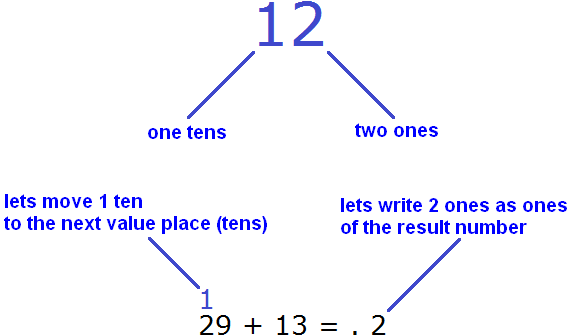
As you can see, we represented 12 ones as 1 tens and 2 ones. We wrote two units in the ones place value of the new number. And we transferred one tens to the place value of tens. We add this tens to the result of adding tens to the numbers 29 and 13. In order not to forget it, we wrote it above the tens of 29.
Now add the tens. Two tens plus one ten will be three tens, plus one tenth left over from the previous addition. As a result, we get four tens in the place value of tens:
![]()
Example 2. Add the digits of 862 and 372.
We start with the ones. The ones of 862 contains the digit 2, and the ones of 372 also contains the digit 2. This means that the ones of 862 contains 2, and the ones of 372 also contains 2. Add 2 ones plus 2 ones- we get 4 ones. Write the number 4 in the ones place value of the new number:
![]()
Then we add the tens. The number 6 is in the range of tens of the number 862, and the number 7 is in the place of tens of the number 372. This means that the place value of tens of the number 862 contains six tens, and the place value of tens of the number 372 contains seven tens. Add 6 tens and 7 tens and we have 13 tens. There is a digit overflow. 13 tens is a tens repeated 13 times. And if we repeat the tens 13 times, we get number 130
10 x 13 = 130
Number 130 consists of three tens and one hundred. We will write three tens in the tens place value of the new number, and we will send one hundred to the next value place:
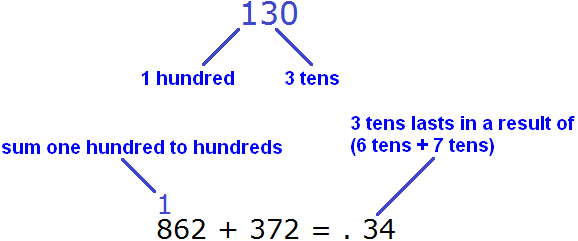
As you can see, we represented 13 tens (number 130) as one hundred and three tens. We wrote three tens in the place value of tens of the new number. And we transferred one hundred to the place value of hundreds. We add this hundred to the result of adding the hundreds to the numbers 862 and 372. In order not to forget it, we wrote it over the hundreds of 862.
Now add up the hundreds. Eight hundreds plus three hundreds is eleven hundreds plus the one hundred left after the previous addition. The result is twelve hundreds in the place value of hundreds:
![]()
Here also an overflow of the hundreds occurs, but it does not lead to an error because the solution is complete. If you wish, you can perform the same operations with 12 hundreds as we did with 13 tens.
Twelve hundreds is a hundred repeated 12 times. And if you repeat a hundred 12 times, you get 1200.
100 x 12 = 1200
The number 1200 has two hundreds and one thousand. Two hundreds are written in the place value of hundreds of the new number, and one thousand is transferred to the place value of thousands.
Now let's look at examples of subtraction. First, let's remember what subtraction is. It is an operation that allows you to subtract another number from one number. You have to subtract by digits, too.
Example 3. Subtract the number 12 from the number 65.
We start with the ones. The ones of 65 contains the digit 5, and the ones of 12 contains the digit 2. This means that the ones of 65 contains five, and the ones of 12 contains 2. Subtract two from five, and we get three. Write number 3 in the ones of the new number:
![]()
Now subtract the tens. The digit 6 is in the place value of tens in the number 65, and the digit 1 is in the place value of tens in number 12. This means that the tens of number 65 contains six tens, and the tens of number 12 contains one ten. Subtract one ten from the six tens, and we have five tens. Write the number 5 in the tens value place of the new number:
![]()
Example 4. Subtract 15 from number 32
The number 32 has two units in the ones digit, and the number 15 has five units in the ones digit. You cannot subtract five from two ones because two ones are less than five ones.
Let's group 32 apples so that the first group contains three tens of apples and the second group contains the remaining two ones of apples:
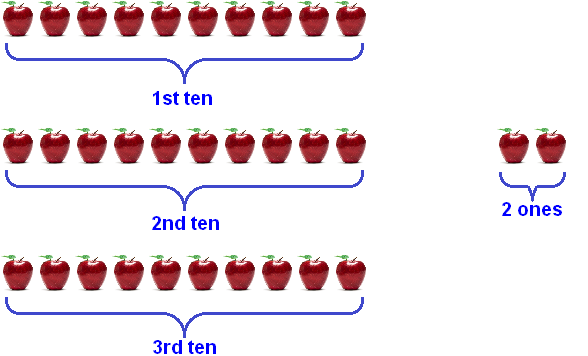
So, we need to subtract 15 apples from these 32 apples, that is, subtract five ones and one tens of apples. And subtract by digits.
You cannot subtract five units of apples from two units of apples. To perform the subtraction, two units must take some apples from the nearest group (digit of tens). But one cannot take as many as one wants because the tens are strictly ordered by ten. The order of tens can only give two units one whole tens.
So, we take one tens from the order of tens and give it to two units:
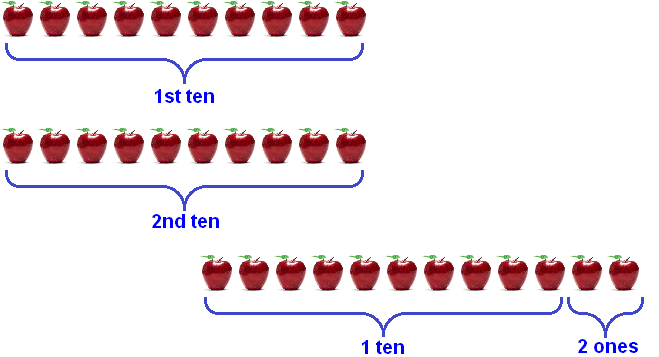
Two units of apples are now joined by one tens of apples. That makes twelve units of apples. And you can subtract five from twelve to get seven. Write the number 7 in the division of units of the new number:
![]()
Now subtract the tens. Because the digit of tens gave up one tens to the ones, it now has not three, but two tens. So we subtract one tens from two tens. This leaves us with one tens. Write number 1 in the tens place value of the new number:
![]()
In order not to forget that one ten (or a hundred or a thousand) was taken (borrowed) from a certain digit (place value), it is important to put a dot over that digit.
Example 5. Subtract 286 from number 653
The unit digit of 653 contains three ones, and the unit digit of 286 contains six ones. Six units cannot be subtracted from the three ones, so we borrow one tens from the digit of tens. Put a dot above that digit of tens to remember that we took one tens from there:
![]()
The one tens and three ones taken together make thirteen ones. Six ones can be subtracted from thirteen ones, which results to seven ones. Write the number 7 in the ones value place of the new number:
![]()
Now subtract the tens. Previously, the tens digit of 653 contained five tens, but we borrowed one tens from it, and now the tens digit contains four tens. You cannot subtract eight tens from four tens, so we take one hundred from the digit of hundreds. We dot the digit of hundreds to remember that we took one hundred from there:
![]()
Taken together, one hundred and four tens make fourteen tens. Eight tens can be subtracted from fourteen tens to make six tens. Write the number 6 in the tens division of the new number:
![]()
Now subtract the hundreds. Previously, the hundreds place value of 653 contained six hundreds, but we took one hundreds from it, and now the hundreds digit contains five hundreds. We can subtract two hundreds from the five hundreds, so we have three hundreds. Write the number 3 in the hundreds digit (value place) of the new number:
![]()
It is much harder to subtract from numbers like 100, 200, 300, 1000, 10000. That is, numbers that have zeros at the end. To perform the subtraction, each digit has to borrow tens/hundreds/thousands from the next digit. Let's see how this happens.
Example 6. Subtract 84 from number 200
Ones number 200 contains zero ones, and ones value place of 84 contains four ones. Four ones cannot be subtracted from zero, so we take one tens from the place of tens. Put a dot above the digit of tens to remember that we took one tens from there:
![]()
But the digit of tens has no tens too, because there is also zero there. In order for the digit of tens to give us one tens, we must take (borrow) one hundred from the digit of hundreds. We dot the digit of hundreds in order to remember that we took from there one hundred for the place value of tens:
![]()
The one hundred which was taken is ten tens. From these ten tens, we take one ten and give it to the ones. This 1 tens and the zero ones together form ten units. From ten ones we can subtract four ones to make six ones. Write the number 6 in the units division of the new number:
![]()
Now we subtract the tens. To subtract the ones, we asked tens for one tens to borrow, but at that time this digit was empty. So that the digit of tens could give us one tens, we took one hundred from the digit of hundreds. This one hundred we called "ten tens." We gave one ten to the ones. So at this point, the division of tens contains not ten, but nine tens. Eight tens can be subtracted from nine tens, resulting in one tens. Write the number 1 in the tens place value of the new number:
![]()
Now subtract the hundreds. For the place value of tens we took one hundred from the digit of hundreds. So now the digit of hundreds contains not two hundreds, but one. Since the subtracted digit of hundreds does not contain the digit of hundreds, we should transfer this one hundred to the digit of hundreds of the new number:
![]()
The final answer is 116.
Naturally, it is quite difficult to perform subtraction using this traditional method, especially at first. Once you understand the principle of subtraction, you can use non-standard methods.
The first method consists in decreasing the number, which has zeros at the end, by one unit. Then subtract from the result the subtracted one and add to the difference the one originally subtracted from the subtracted one. Let's solve the previous example this way:
![]()
The number to decrease here is 200. Decrease this number by one. If you subtract 1 from 200 you get 199. Now, in example 200 - 84, instead of 200 we write down the number 199 and solve example 199 - 84. Solving this example is not too difficult. ones are subtracted from ones, tens from tens, and hundreds are simply transferred to the new number, as there are no hundreds in number 84:
![]()
The answer is 115. Now add to this answer the one we originally subtracted from number 200
![]()
Got the final answer 116.
Example 7. Subtract 91899 from 100000
Subtract one from 100000 to 99999
![]()
Now subtract 9189999 from 99999
![]()
Add to the result 8100 the one we subtracted from 100000
![]()
Got the final answer 8101.
The second method of subtraction is to treat the digit in the digit division as an independent number. Let's solve some examples using this method.
Example 8. Subtract 36 from 75.
Each digit in the digit class is a number in its own right.
So, there are 5 ones in number 75, and there are 6 ones in 36. Six cannot be subtracted from five, so we borrow 1 from the next number, which is in the place value of tens.
Number 7 is in the range of tens. Take one unit from this number and add it to the left side of number 5 in your head
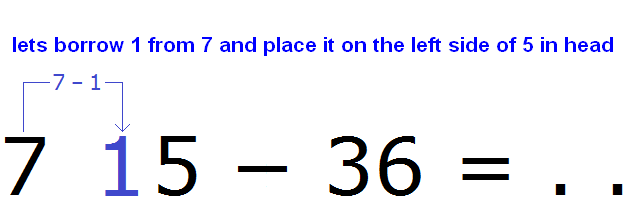
And since one unit is taken from number 7, this number will decrease by one unit and turn into number 6
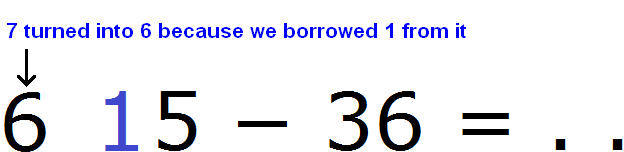
Now the number 15 is in the ones place value of 75, and the number 6 is in the ones place value of 36. You can subtract 6 from 15 to get 9. Write the number 9 in the units place of the new number:
![]()
Now move on to the next number, which is in the range of tens. Previously there was number 7, but we took one unit from this number, so now there is number 6. And in the range of tens of number 36 there is number 3. From 6 you can subtract 3, so that makes 3. Write the number 3 in the tens place of the new number:
![]()
Example 9. Subtract 84 from number 200
![]()
Let's assume that each digit in a digit is an independent number.
So, in the ones digit of 200 there is a zero, and in the ones digit of 84 there is a four. Four cannot be subtracted from zero, so we take one from the next number in the range of tens. But the digit of tens is also zero. Zero cannot give us one. In this case, the next number is 20.
We take one from number 20 and mentally add it to the left of zero, which is in the place of ones. And since one unit is taken from number 20, this number will turn into number 19

Now the number 10 is in the ones place. Ten minus four equals six. Write the number 6 in the units place of the new number:
![]()
Move on to the next number, which is in the range of tens. Previously there was a zero, but this zero along with the next number 2 formed the number 20, from which we took one unit. As a result, the number 20 turned into the number 19. It turns out that now in the range of tens of number 200 is number 9, and in the range of tens of number 84 is number 8. Nine minus eight equals one. Write number 1 in the tens division of our answer:
![]()
Let's move on to the next number, which is in the range of hundreds. Previously there was the number 2, but this number together with the number 0 we took as the number 20, from which we took one unit. As a result, the number 20 turned into the number 19. It turns out that now in the range of hundreds of 200 is the number 1, and in the number 84 range of hundreds is empty, so we move the unit to a new number:
![]()
This method seems complicated and meaningless at first, but in fact it is the easiest way to do such calculations. We will mainly use it when adding and subtracting numbers.
Long addition
Definition. Long addition is a math operation for adding numbers together. Adding in columns is done by digits - ones are added to ones, tens to tens, hundreds to hundreds, thousands to thousands.
Let us have a few examples.
Example 1. Add 61 and 23.
Write first the first number and then the second number, so that the ones and tens of the second number are under the ones and tens of the first number. Write all this with the addition sign (+) vertically:
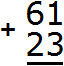
Now add the units of the first number to the units of the second number, and add the tens of the first number to the tens of the second number:
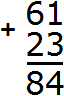
We got 61 + 23 = 84.
Example 2. Add 108 and 60
Write down the numbers in columns. Units under ones, tens under tens:
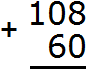
Now add the units of the first number to the units of the second number, the tens of the first number to the tens of the second number, the hundreds of the first number to the hundreds of the second number. But only the first number 108 has hundreds. In this case the number 1 of hundreds is added to the new number (our answer). As they used to say in school, it is "carried off:
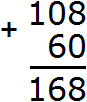
You can see that we blew off the number 1 to our answer.
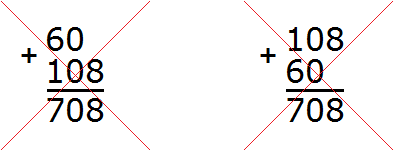
When it comes to addition, it makes no difference in what order to write the numbers. Our example could have been written that way:
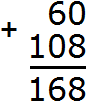
The first entry, where the number 108 was at the top, is more convenient to calculate. A person is free to choose any entry, but it must be remembered that ones must be written strictly under ones, tens under tens, hundreds under hundreds. In other words, the following entries will be wrong:
If suddenly when adding the corresponding digits you get a number which does not fit in the digit of the new number, you must write one digit from the lowest digit and carry the remaining digit to the next digit.
In this case, we are talking about a digit overflow, which we talked about earlier. For example, if you add 26 and 98, you get 124. Let's see how this works.
Let's write the numbers in columns. Units under ones, tens under tens:
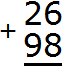
Add the units of the first number to the units of the second number: 6+8=14. We get the number 14, which does not fit in the units digit of our answer. In such cases, we first remove the digit in the units digit of 14 and write it in the units digit of our answer. The digit 4 is in the units digit of 14. Write this digit in the units digit of our answer:
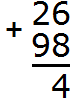
What do we do with the number 1 of 14? Here begins the most interesting part. We move this one to the next digit. It will be added to the tens digit of our answer.
We add tens to tens. 2 plus 9 equals 11, plus we add the one we got from number 14. Adding our unit to 11 gives us the number 12, which we write in the tens digit of our answer. Since this is the end of the solution, it is no longer a question of whether the answer will fit in the place of tens. We write down 12 in its entirety, forming the final answer.
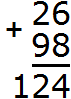
The answer is 124.
Speaking by the traditional method of addition, adding 6 and 8 units results in 14 units. 14 units is four ones and one tens. We wrote four units in the category of units, and one tens was sent to the next category (to the category of tens). Then we added 2 tens and 9 tens to get 11 tens, plus we added 1 tens which was left when we added units. The result was 12 tens. We wrote down these twelve tens in their entirety, forming the final answer 124.
This simple example demonstrates the school situation in which they say "four in writing, one in mind. If you are going to solve examples and you have a digit left over after adding the digits, write it above the digit where it will be added. That way you won't forget it:
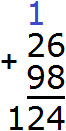
Example 2. Add up the numbers 784 and 548.
Write the numbers in columns. Units under ones, tens under tens, hundreds under hundreds:
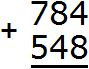
Add the units of the first number to the units of the second number: 4+8=12. 12 does not fit into the order of units of our answer, so we remove digit 2 from the order of units from 12 and write it in the order of units of our answer. And we carry digit 1 to the next digit:
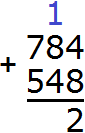
Now add the tens. Add 8 and 4 plus the one left over from the previous operation (the one left over from 12, it is highlighted in blue in the picture). We add 8+4+1=13. The number 13 will not fit in the digit of tens of our answer, so we will write the number 3 in the digit of tens, and the unit will be moved to the next digit:
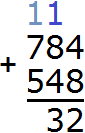
Now we add hundreds. Add 7 and 5 plus the one left over from the previous operation: 7+5+1=13. Write the number 13 in the row of hundreds:
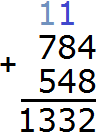
Long subtraction
Example 1. Subtract number 53 from number 69.
Write down the numbers in columns. Units under ones, tens under tens. Then subtract by digits. Subtract the units of the first number from the units of the second number. Subtract the tens of the first number from the tens of the second number:
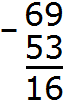
We got the answer 16.
Example 2. Find the value of the expression 95 - 26
Write the expression in columns:
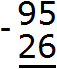
The units digit of 95 contains 5 units, and the units digit of 26 contains 6 units. Six units cannot be subtracted from five units, so we take one tenth from the digit of tens. This tens and the five available units together make 15 units. From 15 units we can subtract 6 units, which makes 9 units. Write the number 9 in the units division of our answer:
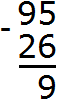
Now subtract the tens. The range of tens of the number 95 used to contain 9 tens, but we took from this range one tens, and now it contains 8 tens. And the range of tens of the number 26 contains two tens. Two tens can be subtracted from eight tens to make six tens. Write the number 6 in the tens digit of our answer:
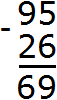
Let's use an unconventional subtraction method in which each digit included in the number is treated as a separate number. When subtracting large numbers in columns, this method is very convenient.
The number 5 is in the order of the units of the subtractor. The number 6 is in the order of the units of the subtractor. So we take one unit from number 9. The taken unit is mentally added to the left of the five. And since we took one unit from number 9, the number will be reduced by one unit:
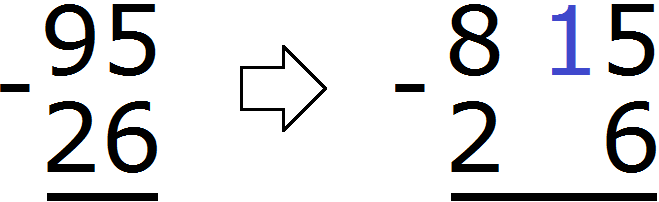
As a result, five turns into 15. Now you can subtract 6 from 15. You get 9. Write 9 in the units division of our answer:
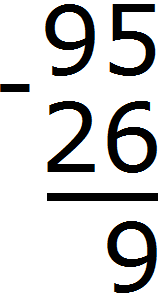
Let's go to the number of tens. The number 9 used to be there, but because we took one unit from it, it turned into number 8. In the tens division of the second number is the number 2. Eight minus two is six. Write number 6 in the decimal place of our answer:
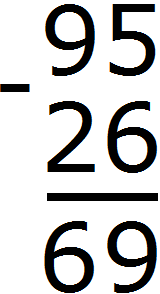
Example 3. Find the value of the expression 2412 - 2317
Write down this expression in the column:
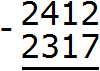
The number 2 is in the unit digit of 2412, and the number 7 is in the unit digit of 2317. You can't subtract a seven from a two, so we take one from the next number 1. We mentally add the taken one to the left of the two:
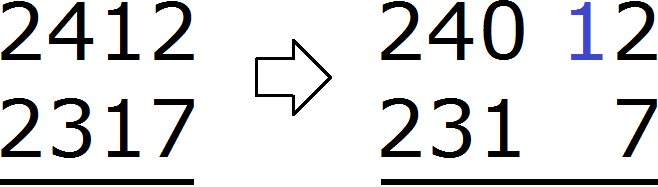
As a result, the two converts to the number 12. Now you can subtract 7 from 12. You get 5. Write the number 5 in the units division of our answer:
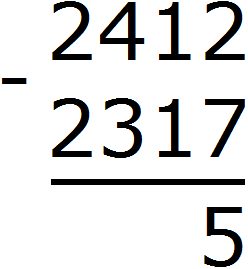
Let's move on to tens. In the range of tens of 2412 there was previously a number 1, but because we took from it one unit, it turned into 0. And in the range of tens of 2317 there is a number 1. From zero you cannot subtract one. So we take one from the next number 4. We mentally add one to the left of zero. And since we took one unit from number 4, the number will decrease by one:
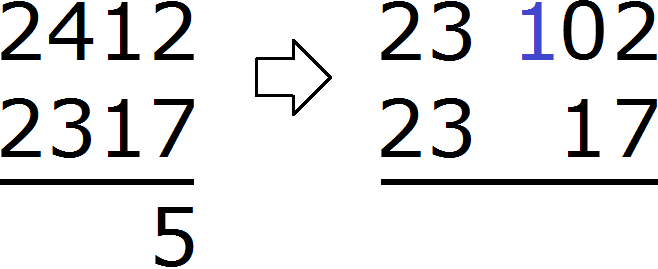
As a result, zero is converted to 10. Now you can subtract 1 from 10. You get 9. Write 9 in the decimal place of our answer:
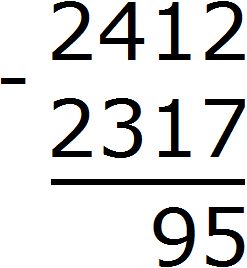
The hundredths digit of 2412 used to contain the number 4, but now it contains the number 3. The hundredths digit of 2317 also has the number 3. Three minus three equals zero. It's the same with the bits of thousands in both numbers. Two minus two equals zero. And if the difference of the higher digits equals zero, then this zero is not written down. Therefore, the final answer is number 95.
Example 4. Find the value of the expression 600 - 8
Let's write the expression in columns:
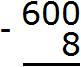
The unit digit of 600 contains zero, and the unit digit of 8 contains the number itself. You can't subtract an eight from zero, so we take one from the next number. But the next number is also zero. Then for the next number we take the number 60. We take one from that number and mentally add it to the left of zero. And since we took one unit from number 60, that number will decrease by one unit:

Now the number 10 is in the ones place. You can subtract 8 from 10 to get 2. Write the number 2 in the units place of the new number:
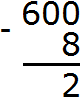
Move on to the next number, which is in the range of tens. In the range of tens used to be zero, but now there is a number 9, and in the second number the range of tens is absent. Therefore, the number 9 is moved to the new number:
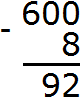
Move on to the next number, which is in the range of hundreds. In the range of hundreds there used to be number 6, but now there is number 5, and in the second number the range of hundreds is absent. Therefore, the number 5 is transferred to the new number:
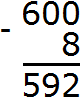
Example 5. Find the value of the expression 10000 - 999
Write the expression in the column:
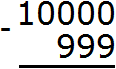
In the units digit of 10000 there is a 0, and in the units digit of 999 there is a 9. You cannot subtract a nine from a zero, so we take one from the next number in the tens division. But the next digit is also zero. Then we take 1000 as the next number and take one from that number:
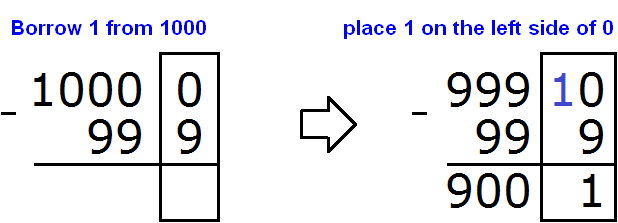
The next number in this case was 1000. By taking one from it, we converted it to 999. We added the one we took to the left of the zero.
Further calculation was not too difficult. Ten minus nine equaled one. Subtraction of the numbers in the tens division of both numbers gave zero. Subtracting the numbers in the hundred division of both numbers also yielded zero. And the nine in the thousands division was transferred to the new number:
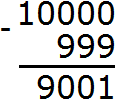
Example 6: Find the value of the expression 12301 - 9046
Let's write the expression in the column:
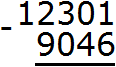
The unit digit of 12301 contains the number 1, and the unit digit of 9046 contains the number 6. Six cannot be subtracted from one, so we take one from the next number in the tens digit. But in the next digit is zero. Zero can not give us anything. Then for the next number we take 1230 and take one from it:
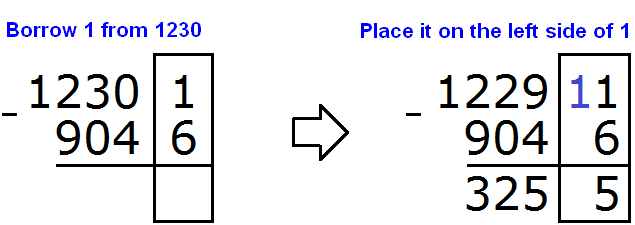
The next number in this case was 1230. By taking one from it, we converted it to 1229. And we mentally added the taken unit to the left of the unit in the division of units.
The further calculation was not difficult. Eleven minus six equaled five. Subtracting the numbers in the tens order of both numbers gave the number five. Subtracting numbers in the hundredths order of both numbers gave the number 2. Subtracting the numbers in the thousands division of both numbers gave the number 3.

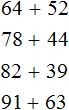
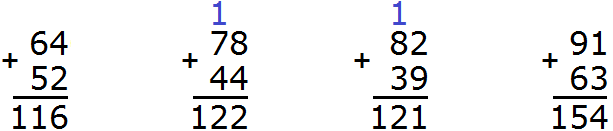
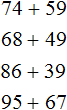
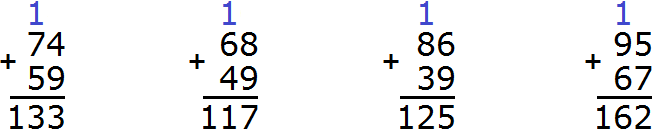
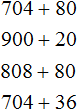
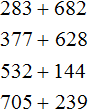
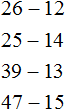

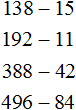
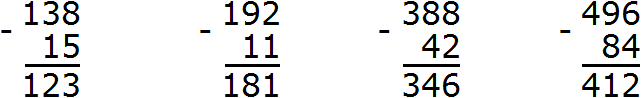
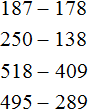

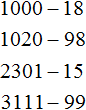
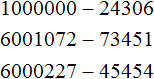
Comments