Solving inequalities with a module by the method of intervals

If an inequality contains two or more modules, it is more convenient to solve it by the method of intervals.

The process of solving inequalities with moduli using the interval method is much like the process of solving equations with moduli using the interval method.

Let's look at a few examples.

Example 1. Solve the inequality |7 - x|+|2x + 3|< 16

Solution

First, we find x such that the submodular expressions 7 - x and 2x + 3 are zero. To do this, equate these expressions to zero and solve the simplest linear equations:

inequalities with module interval method Fig. 1

Mark the numbers 7 and minus three second on the coordinate line. Mark the smaller numbers to the left, the larger to the right:

inequalities with module interval method Fig. 2

Now we have three intervals: inequalities with module interval method Fig. 4, inequalities with module interval method Fig. 5, and inequalities with module interval method Fig. 6. Now we need to solve the original inequality on each of these intervals. Keep in mind that on each of these intervals the modules of the original inequality may be solved differently.

Solve the initial inequality on the first interval inequalities with module interval method Fig. 4

Then we reason like this:

If inequalities with module interval method Fig. 4, then for any value of x on this interval the submodular expression 7 - x becomes non-negative, and hence the module |7 - x| on the interval inequalities with module interval method Fig. 4 will expand with the plus sign. The second module |2x + 3| on the interval inequalities with module interval method Fig. 4 will expand with the minus sign.

Then as a result of moduli expansion on the interval inequalities with module interval method Fig. 4 the initial inequality will look like:

inequalities with module interval method Fig. 9

Let's solve this inequality:

inequalities with module interval method Fig. 7

So now we consider the interval inequalities with module interval method Fig. 4. And by solving the original inequality on this interval, we get the inequality x > -4.

Now begins the most interesting part. We need to find out if the inequality x > -4 is satisfied on the interval inequalities with module interval method Fig. 4. Or ask this question: "For what values of the interval inequalities with module interval method Fig. 4 the inequality x > -4 is satisfied".

For clarity, let's draw another coordinate line and draw the solutions to the inequalities x > -4 and inequalities with module interval method Fig. 4 on it

inequalities with module interval method Fig. 8

The figure shows at which values of interval inequalities with module interval method Fig. 4 the inequality x > -4 holds. These values are between -4 and minus three second

So our first solution would be a range of -4 to minus three second

inequalities with module interval method Fig. 20

Now solve the initial inequality on the interval inequalities with module interval method Fig. 5

If inequalities with module interval method Fig. 5, then for any value of x on this interval the submodular expression 7 - x becomes non-negative, which means that the module |7 - x| on the interval inequalities with module interval method Fig. 5 will expand with the plus sign. The second module |2x + 3| on interval inequalities with module interval method Fig. 5 will also expand with the positive sign.

After exposing the modules on interval inequalities with module interval method Fig. 5, the original inequality will look like this:

inequalities with module interval method Fig. 10

Solve this inequality:

inequalities with module interval method Fig. 11

Now we are looking at the interval inequalities with module interval method Fig. 5. And by solving the original inequality on this interval we obtained the inequality x < 6. Now we need to find out if the inequality x < 6 holds at inequalities with module interval method Fig. 5

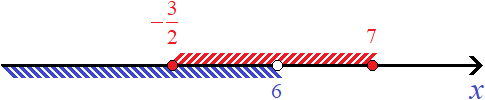
inequalities with module interval method Fig. 13

The inequality x < 6 is not fulfilled on the whole interval inequalities with module interval method Fig. 5, but only on the interval minus three second to 6. Write down our second solution:

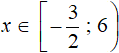
inequalities with module interval method Fig. 21

Now solve the original inequality on the last interval inequalities with module interval method Fig. 6

If inequalities with module interval method Fig. 6, then for any value of x on this interval the submodular expression 7 - x becomes negative, and hence the module |7 - x| on the interval inequalities with module interval method Fig. 6 will expand with a minus sign. The second module |2x + 3| at interval inequalities with module interval method Fig. 6 will expand with the positive sign.

Then as a result of moduli expansion on the interval inequalities with module interval method Fig. 6 the initial inequality will look like:

inequalities with module interval method Fig. 14

Solve this inequality:

inequalities with module interval method Fig. 15

Now we consider the interval inequalities with module interval method Fig. 6. And by solving the original inequality on this interval we have obtained the inequality inequalities with module interval method Fig. 17. Now we need to find out if the inequality inequalities with module interval method Fig. 17 holds at inequalities with module interval method Fig. 6

inequalities with module interval method Fig. 16

We see that inequality inequalities with module interval method Fig. 17 is not fulfilled for any value of interval inequalities with module interval method Fig. 6. This means that the original inequality on the interval inequalities with module interval method Fig. 6 has no solutions.

Indeed, take any number from the interval inequalities with module interval method Fig. 6, for example, the number 9, and substitute it into the original inequality. The result is an inequality that does not hold:

inequalities with module interval method Fig. 18

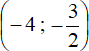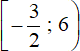
Now we need to piece together the answers we got at each interval. To do this, simply combine intervals inequalities with module interval method Fig. 22 and inequalities with module interval method Fig. 23

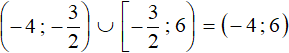
inequalities with module interval method Fig. 24

Answer: (−4 ; 6).

Example 2. Solve an inequality: 3|x âˆ’ 2|+|5x âˆ’ 4| â‰¤ 10

Solution

Find x, at which the submodular expressions x - 2 and 5x - 4 are zero. To do this, equate these expressions to zero and solve the simplest linear equations:

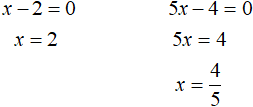
inequalities with module interval method Fig. 25

Mark the numbers 2 and inequalities with module interval method Fig. 26 on the coordinate line:

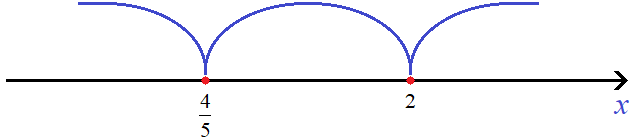
inequalities with module interval method Fig. 27

Solve the original inequality on the interval inequalities with module interval method Fig. 28. Both modules on this interval are expanded with minus:

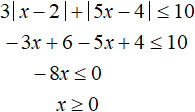
inequalities with module interval method Fig. 29

The resulting inequality x ≥ 0 is not satisfied over the entire interval inequalities with module interval method Fig. 28, but only over the interval 0 to inequalities with module interval method Fig. 26

inequalities with module interval method Fig. 38

Now solve the original inequality on the next interval inequalities with module interval method Fig. 30. On this interval the module |x - 2| expands with a minus, and the module |5x - 4| with a plus:

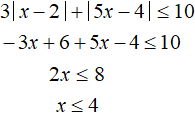
inequalities with module interval method Fig. 31

The resulting inequality x ≤ 4 holds over the whole interval inequalities with module interval method Fig. 30. Thus on the interval inequalities with module interval method Fig. 30 the original inequality has the following solution:

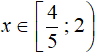
inequalities with module interval method Fig. 39

Solve the original inequality on the next interval x ≥ 2. Both modules on this interval are expanded with a plus:

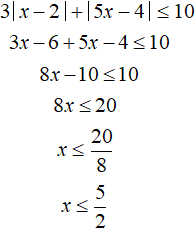
inequalities with module interval method Fig. 32

The resulting inequality inequalities with module interval method Fig. 33 is not satisfied on the entire interval x ≥ 2, but only on the interval from 2 to five second

inequalities with module interval method Fig. 40

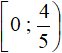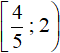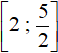
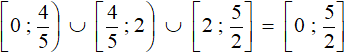
Let's write down the final answer. To do this, combine the intervals inequalities with module interval method Fig. 34, inequalities with module interval method Fig. 41 and inequalities with module interval method Fig. 35 inequalities with module interval method Fig. 36

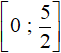Answer: inequalities with module interval method Fig. 37.

Tasks for independent decision

Task 1. Solve an inequality:
Solution:
Answer: .
Show Solution
Task 2. Solve an inequality:
Solution:
Answer: no solutions.
Show Solution
Task 3. Solve an inequality:
Solution:
Answer: .
Show Solution
Task 4. Solve an inequality:
Solution:
Answer: .
Show Solution
Task 5. Solve an inequality:
Solution:
Answer: .
Show Solution

Add comment

1. If you don't understand something, you can ask a question through the form below
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.

Security code
Refresh

  • You are here:  
  • Home >>
  • 74. Solving inequalities with module by method intervals