The basic operations used in mathematics are addition, subtraction, multiplication, and division.
In addition to these operations, there are also inequalities (relational operators):
- equals (=),
- greater than (>),
- less than (<),
- greater than or equal to (≥),
- less than or equal to (≤),
- not equal (≠).
Inequalities (Relation operations)
The word "relation" speaks for itself.
Lets start with an example: Object A is related to Object B. Dad has a relation to Mom. This relation is called a marriage:

Examples of relationships abound.
We can say that our beautiful world, which develops harmoniously, also consists of relationships.
If 5 > 3, we say that "five is greater than three" and write it as 5 > 3 (read: five is greater than three). The acute angle of the '>' sign must point toward the smaller number. In our example, the number 3 was smaller than the number 5, so the acute angle of the ratio pointed toward the number 3.
Another example.
The number 11 is smaller than the number 15. This phrase can be written as follows:
11 < 15
In mathematics, you can use inequalities to write laws, formulas, equations, and functions. You can write that one expression is equal to another, or some action is unacceptable with respect to some object, number, law.
The famous phrase "you cannot divide by zero" is written as follows:
![]()
Let us simply say that this expression may contain any numbers instead of a and b. But then it is said that b must not be equal to zero.
Definition. The equal sign = is placed between the quantities and indicates that these quantities are equal to each other.
For example, "five equals five" is written as 5 = 5. It is clear that this two similar digits are equal to each other. In addition to simple numbers, an equal sign can describe more complex expressions, for example: 9 + x + y = 4 + 5 + x + y.
Another example: If one big watermelon weighs 20 kg and two small watermelons weigh 10 kg each, then we can put an equal sign between a watermelon that weights 20 kg and two watermelons with 10 kg weight. This relation can be read as "one watermelon (20 kilograms) equals the weight of two watermelons (10 kilograms each)".
After all, 20 kg = 10 kg + 10 kg.
This observation is equivalent to the mathematical expression "10 + 10 = 20"

Definition. The sign not equal ≠ is placed between values when they are not equal to each other.
For example, 5 ≠ 7. Clearly, five is not equal to seven.
an A is not equal B, a dog is not equal to a cat, a tangerine is not an orange:
A student ≠ an underachiever
dog ≠ cat
mandarin ≠ orange
You can look around you and find many examples of relationships that can be interpreted in terms of mathematics.
Addition
Definition. The plus sign symbol (+), indicates addition and is used when combining two values.
The result from bringing them together is called the sum.
For example, 3 is added to 2.
Write 3 + 2 = 5
In this example, 3 is the summand, 2 is the second summand, and 5 is the result sum.
In the future we will have to add quite large numbers. But combining this big numbers will eventually come down to combining small numbers.
So you have to learn how to add small numbers between 0 and 9. For example:
2 + 2 = 4
3 + 4 = 7
7 + 2 = 9
0 + 7 = 7
You can practice by writing down some simple examples in your notebook. Believe me, there's no shame in it.
Subtraction
Definition. The subtraction is signified by the minus sign (-) and is used when taking one number away from another.
For example, subtract 2 from 10.
10 − 2 = 8
In this example, number 10 is the minuend, number 2 is the subtrahend, and number 8 is the difference.
Multiplication
Definition. Multiplication is signified by the multiplication sign (×) and is used when one number is multiplied by another. The word multiplication speaks for itself - some number is multiplied by a certain number of times, i.e. multiplied.
For example, writing 4 × 3 means that a four will be multiplied by a factor of three during the multiplication operation.
the multiplication of two numbers is equivalent to adding as many copies of one of them, the multiplicand, as the quantity of the other one, the multiplier. The result of a multiplication operation is called a product.
Multiplication is when you take one number and add it together a number of times.
For example, multiply the number 4 by 3.
4 × 3 = 12
In this example, 4 is the multiplicand, 3 is the multiplier, and 12 is the product.
4 × 3 can be understood as "Take 4 and add it together three times". For example, if we have four candies and we add it together three times, we will have twelve candies:
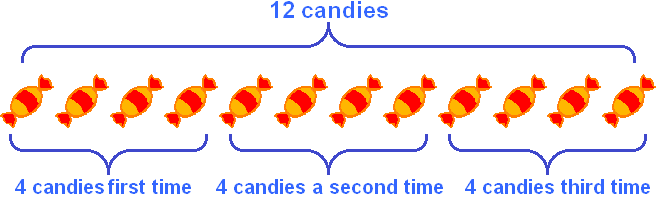
In other words, multiplying 4 by 3 can be understood as the sum of 4 three times. It looks like this:
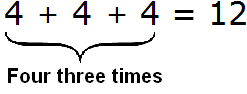
Multiplication is when you take one number and add it together a certain number of times. Suppose there are candies in a vase.
Let's take four candies once:
4 candies × 1 = 4 candies.
We will have four candies in our hands.
Let's try to take four candies 2 times:
4 candies × 2 = 8 candies.
We will have eight candies in our hands.
Let's try to take four candies zero times, that is, none:
4 × 0 = 0
We won't have any candy in our hands because we did never take it. Therefore, multiplying any number by zero gives a zero as the answer.
In some books, both numbers from multiplication can be referred to as factors. For example, 4 × 3, the multiplier is 4 and the multiplier is 3, but these two numbers can still be called the factors. It will not be a mistake.
In the future, we are going to multiply some pretty big numbers. But multiplying big numbers comes down to multiplying small numbers. So first we have to learn how to multiply small numbers.
Fortunately all of simple numbers are already multiplied and written in a special table, which is called the Multiplication table. If you live in Russia or in the former Soviet Union, you probably know this table by heart. If you don't, be sure to learn it!
Division
Definition. It is signified by the division sign (÷ or : ) and is used when dividing numbers. The division is a method of distributing a group of things into equal parts.
the number that is being divided in the division process is called a dividend.
The number by which dividend is being divided by is called divisor.
The result obtained in the division process is a quotient.
For example, divide 10 by 2.
10 : 2 = 5
In this example, number 10 is the dividend, number 2 is the divisor, and number 5 is the quotient.
If we have ten candies and we divide them into two parts, each part will have five candies:

This is how you can understand the meaning of 10 : 2 = 5.
Exercises
Most people will solve these problems in their heads easily. However, it is recommended that you do these tasks in a notebook with a pencil in your hand. You should get used to math by solving simple examples.
Comments
That's right, I forgot to add, sorry))) But now I'm busy with work, try to come up with it yourself.
Division is an inverse operation to multiplication, so if with multiplication we have 5 * 3 = 5 + 5 + 5 as you said, then in division we just have to find such an X that we can substitute in this series of summands and get the result 15 / 3 = X + X + X.
We have to find three equal parts of X which together would give 15
35 / 7: we must find such 7 equal parts of X that would add up to 35. And so on.
Is there a similar way to describe division? Intuition would lead us to say that division is shorthand notation for subtraction but, upon, further inspection, that intuition would be incorrect. Is there some more fundamental way one can understand division? What’s happening behind the scenes in a division operation?
Thank you for finding the error, I will correct it now. Right - 4 is the multiplicand
At one time I neglected learning math, but now I need it.
My goal is to reach a certain level, and your site helps me a lot.
Thank you so much for everything!