Basic information
To find the area of a square, you need to take the length of its side to the second power.
Find the area of the square whose side length is 3 cm
S = 32 = 9 cm2
Now solve the inverse task. Namely, knowing the area of the square we will determine the length of its side. To do this we will use such a tool as a root. A root can be a square, a cube, or the n-th power.
Now we are interested in the square root. It is otherwise known as the 2nd-power root.
To find the length of the side of our square, we need to find a number whose second power is 9. This is number 3. This number is the root.
Let's introduce a new symbol for working with roots.
The root symbol looks like 
. This is because the word root is used in mathematics as a radical. And the word radical comes from the Latin radix (which means root). The first letter of the word radix is r, which was later transformed into the root symbol .
Under the root there is a sub-root expression. In our case, the sub-root expression is number 9 (the area of the square).
We were interested in the square root (aka the second power root), so we put the number 2 on the left above the root. This number is called the index of the root (or the power of the root)
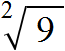
We got an expression that reads like this: "the square root of 9. From this point on, a new task arises to find the root itself.
If you take number 3 to the second power, you get number 9. Therefore, number 3 is the answer:
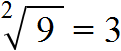
So a square with an area of 9 cm2 has a side whose length is 3 cm. The above action is called extraction of the square root.
It is not hard to guess that the square root of 9 is also a negative number -3. Its exponent in the second power also yields the number 9
It turns out that expression 
has two values: 3 and -3. But the length of the side of the square cannot be a negative number, so for our task the answer is only one, namely 3.
In general, the square root has two opposite values: positive and negative.
For example, extract the square root from the number 4
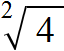
This expression has two values: 2 and -2, because if you take these numbers to the second power, you get the same result 4
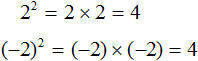
Therefore, the answer to an expression of the form 
is written with a plus and a minus. Plus and minus means that the square root has two opposite values.
Write down the answer to the expression 
with plus and minus:
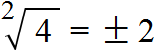
Definitions
Let's define the square root.
The square root of a is a number b whose second power is equal to a.
That is, the number b must be such that the equality b2 = a is fulfilled. The number b (aka the root) is denoted by the radical such that 
. In practice, the left and right parts are swapped and we see the usual expression 
For example, the square root of number 16 is number 4, because number 4 to the second power is 16
42 = 16
Root 4 can be denoted by the radical 
so that 
.
Also, the square root of 16 is -4, since -4 to the second power is 16
(−4)2 = 16
If only a positive value is of interest when solving a task, then the root is not just called a square root, but an arithmetic square root.
The arithmetic square root of a is a non-negative number b (b ≥ 0) at which the equality b2 = a is satisfied.
In our example, the square roots of number 16 are roots 4 and -4, but only the root of 4 is arithmetic.
In colloquial language, you can use an abbreviation. For example, the full expression reads "the square root of sixteen", while the abbreviated version reads "the root of sixteen".
The terms root and square should not be confused. A square is a number that is the result of raising any number to the second power. For example, the numbers 25, 36, 49 are squares because they are the result of raising numbers 5, 6, and 7 to the second power, respectively.
The roots are 5, 6, and 7. They are those numbers which, to the second power, are 25, 36, and 49, respectively.
Most often in square roots, the exponent of the root is not specified at all. For example, instead of writing you can use the notation 
. If you find a root without an exponent in a math textbook, you should know it is a square root.
The square root of one is equal to one. That is, the following equality is true:
This is because one to the second power equals one:
12 = 1
and a square consisting of one square unit has a side equal to one:
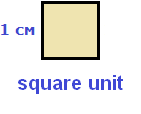
The square root of zero is zero. That is, equality 
is true because 02 = 0.
An expression of the form 
makes no sense. For example, the expression 
makes no sense, because the second power of any number is a positive number. It is impossible to find a number whose second power is -4.
If an expression of the form 
is raised to the second power, that is, if we write 
, then this expression will be equal to the sub-root expression a
For example, expression 
equals 4
This is because expression 
is equal to 2. But that value is immediately raised to the second power and the result is 4.
More examples:
The root of the square of a number is equal to the modulus of that number:
For example, the root of number 5 raised to the second power is equal to the modulus of number 5
If a negative number is raised to the second power, the answer will again be positive. For example, the root of -5 raised to the second power is equal to the modulus of -5. And the modulus of -5 is 5
Indeed, if, without using the 
rule, we calculate expression 
by the usual method - first raising the number -5 to the second power, then extracting the result, we get the answer 5
The rule should not be confused with the 
rule. The rule is true for any a, while the rule is true if the expression makes sense.
In some textbooks, the root sign may appear without the top line. It looks like this:
Examples: √4, √9, √16.
A smaller number corresponds to a smaller root, and a larger number corresponds to a larger root.
For example, consider the numbers 49 and 64. The number 49 is smaller than the number 64.
49 < 64
If you extract the square roots from these numbers, then to number 49 corresponds the smaller root, and to number 64 the larger root. Indeed, √49 = 7, and √64 = 8,
√49 < √64
Hence:
7 < 8
Examples of square root extraction
Let's look at some simple examples of square root extraction.
Example 1. Extract the square root of √36
This square root is equal to a number whose square is 36. This is number 6, because 62 = 36.
√36 = 6
Example 2. Extract the square root of √49
This square root is equal to a number whose square is 49. This is number 7, because 72 = 49.
√49 = 7
In such simple examples, it is enough to know the multiplication table. For example, we remember that the number 49 is part of the multiplication table by seven. That is:
7 × 7 = 49
But 7 × 7 is 72
72 = 49
Hence, √49 = 7.
Example 3. Extract the square root of √100
This square root is equal to a number whose square is 100. This is number 10, because 102 = 100
√100 = 10
The number 100 is the last number whose root can be extracted using the multiplication table. For numbers greater than 100, square roots can be found using the square table.
Example 4. Extract the square root of √256
This square root is a number whose square is 256. To find this number, use the table of squares.
Find the number 256 in the table of squares and moving from it to the left and up determine the digits that form the number whose square is 256
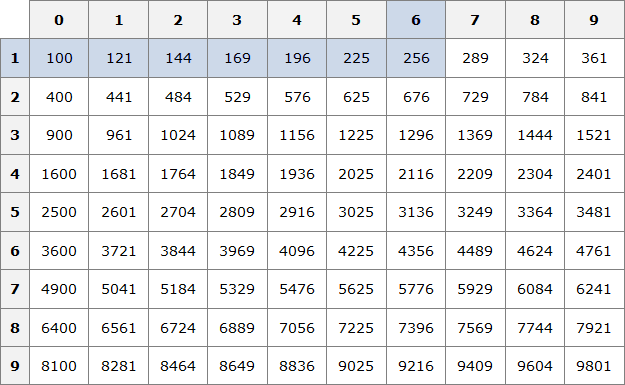
We see that this number is 16. So √256 = 16.
Example 5. Find the value of the expression 2√16
In this example, the number 2 is multiplied by the expression with the root. First calculate the root √16, then multiply it with number 2
Example 6. Solve equation 
In this example, you need to find the value of the variable x where the left-hand side equals 4.
The value of the variable x is 16, because 
. So the root of the equation is 16.
Note. The root of an equation should not be confused with the square root. The root of an equation is the value of the variable at which the equation converts to a valid numerical equality. And a square root is a number whose second degree is equal to the expression below the radical .
Similar examples are solved using the definition of the square root. Let us do the same.
We know from the definition that the square root of is equal to the number b at which the equality b2 = a is satisfied.
Let us apply the equality b2 = a to our example . The variable b is number 4, and the variable a is the expression under the root of 
, namely, the variable x
In the expression 42 = x, calculate the left-hand side, we obtain 16 = x. Swap the left and right parts, and we obtain x = 16. As a result, we find the value of the variable x.
Example 7. Solve equation 
Move -8 to the right side, changing the sign:
Let's raise the right part to the second power and equate it to the variable x
Calculate the right part, we get 64 = x. Swap the left and right parts, we get x = 64. So the root of equation is 64.
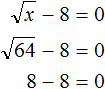
Example 8. Solve equation 
Let's use the definition of the square root:
Variable b is number 7, and variable a is the sub-root expression 3 + 5x. Let us raise number 7 to the second power and equate it to 3 + 5x
In the expression 72 = 3 + 5x we calculate the left-hand side and obtain 49 = 3 + 5x. This is an ordinary linear equation. Solve it:
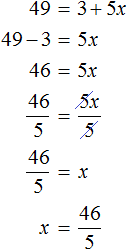
The root of the equation is 
. Let us check it by substituting it into the original equation:
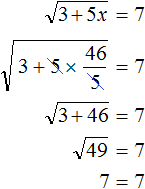
Example 9. Find the value of expression 
In this expression, number 2 is multiplied by the square root of number 49.
First extract the square root and multiply it with number 2
The approximate value of the square root
Not every square root can be extracted. You can extract a square root only if you can find a number whose second power is equal to the sub-root expression.
For example, you can extract the square root of 
because you can find a number whose second power is equal to the square sub-root expression. This is the number 8, because 82 = 64. That is, 
And it is impossible to extract the square root of 
because it is impossible to find a number whose second power equals 3. In this case it is said that the square root of number 3 cannot be extracted.
But it is possible to extract the square root of number 3 by approximation. To extract the square root approximately means to find a value that, when taken to the second power, is as close to the sub-root expression as possible.
The approximated value is searched for with a certain accuracy: accurate to integers, accurate to tenths, accurate to hundredths, and so on.
Find the value of root approximately to the nearest tenth. The phrase "to the nearest tenth" indicates that the approximate value of root will be a decimal fraction with one digit after the point.
First, let's find the nearest smaller number, the root of which can be extracted. This is number 1. The root of this number is equal to the number itself:
√1 = 1
Similarly, find the nearest larger number, the root of which can be extracted. This is the number 4. The root of this number is 2
√4 = 2
√1 is less than √4
√1 < √4
And √3 is greater than √1 but less than √4. Let us write it as a double inequality:
√1 < √3 < √4
The exact values of the roots √1 and √4 are known. These are numbers 1 and 2
1 < √3 < 2
Then it is obvious that the value of the root √3 will be a decimal, because there are no integers between the numbers 1 and 2.
To find an approximate value of the square root of √3, we will check the decimal fractions between 1 and 2 by squaring them. We will do this until we get a value as close to 3 as possible. Let's check for example the fraction 1.1
1.12 = 1.21
The result is 1.21, which is not very close to 3. So 1.1 is not suitable as an approximation for the square root of √3, because it is small.
Let's check then the fraction 1.8
1.82 = 3.24
The result is 3.24, which is close to the sub-root expression, but exceeds it by 0.24. So 1.8 is not suitable as an approximation to the √3 root, because it is large.
Let's check then the fraction 1.7
1.72 = 2.89
The result is 2.89, which is already close to the approximate sub-root expression. So 1.7 is the approximate value of the square root of √3. Recall that the sign of the approximation looks like ≈
√3 ≈ 1.7
The value 1.6 does not need to be checked, because the result is 2.56, which is further from three than the value 2.89. And the value of 1.8, as shown earlier, is already large.
In this case, we found an approximate value of the root √3 to the nearest tenth. The value can be obtained even more accurately. To do this, it must be found to the nearest hundredth.
To find the value to within a hundredth, check the decimals between 1.7 and 1.8
1.7 < √3 < 1.8
Let's check the fraction 1.74
1.742 = 3.0276
The result is 3.0276, which is close to the sub-root expression, but exceeds it by 0.0276. So the value of 1.74 is large for the √3 root.
Let's check then the fraction 1.73
1.732 = 2.9929
The result is 2.9929, which is close to the sub-root expression √3. So 1.73 would be an approximation to the square root of √3 to the nearest hundredth.
The process of finding an approximate value of a square root goes on indefinitely. Thus, the √3 root can be found to the nearest thousandths, ten thousandths, and so on:
√3 = 1.732 (calculated to the nearest thousandths)
√3 = 1.7320 (evaluated to within ten thousandths)
√3 = 1.73205 (evaluated to the nearest hundred thousandths).
Another square root can be extracted to integers. The approximated value of the square root √3 to integers is one:
√3 ≈ 1
The value 2 would be too large, because taking this number to the second power results in number 4, which is larger than the sub-root expression. We are interested in values that, when raised to the second power, are equal to the sub-root expression or as close to it as possible, but do not exceed it.
Depending on the task at hand, it is allowed to find a value whose second power is greater than the square root. This value is called the approximate value of the square root with excess. Let's talk about this in more detail.
The approximated value of the square root with a deficiency and an excess
Sometimes you may encounter an task that requires you to find an approximate value of a root with a deficiency or excess.
In the previous topic, we found an approximate value of the root √3 to the nearest tenth with a deficiency. Deficiency is understood in the sense that we lacked some more parts to the value of 3. Thus, by finding an approximate value of √3 to the nearest tenth, we obtained 1.7. This value is a value with a deficiency, because if you take this number to the second power, you get the result 2.89. This result lacks another 0.11 to get number 3. That is, 2.89 + 0.11 = 3.
Excess values are approximations that, when taken to the second power, yield a result that exceeds the sub-root expression. For example, by calculating the √3 root as an approximation, we checked the value 1.8. This value is an approximation of the √3 root, to the nearest tenth, since taking 1.8 to the second power gives you 3.24. This result exceeds the sub-root expression by 0.24. That is, 3.24 - 3 = 0.24.
The approximate value of the square root √3 to integers was also found with a deficiency:
√3 ≈ 1
This is because when you squared one, you get one. That is, the number 3 is still two short.
The approximated value of the square root √3 can also be found to the nearest integer with an excess. Then this root is approximated by 2
√3 ≈ 2
This is because when you squared 2, you get 4. The number 4 exceeds the sub-root expression 3 by one. When approximating the square root with an excess, it is desirable to specify that the root is extracted with an excess:
√3 ≈ 2 (with excess)
Because an approximation is more often sought with a deficiency than with an excess.
Additionally, it should be mentioned that in some textbooks the phrases "to the nearest integer", "to the nearest tenth", "to the nearest hundredth", are replaced by "to the nearest 1", "to the nearest 0.1", "to the nearest 0.01" respectively.
For example, if the assignment says to extract the square root of number 5 to the nearest 0.01, then this means that the root should be extracted approximately to the nearest hundredth:
√5 ≈ 2.23
Example 2. Extract the square root of 51 to the nearest 1
√51 ≈ 7
Example 3. Extract the square root of 51 to the nearest 0.1
√51 ≈ 7.1
Example 4. Extract the square root of 51 to the nearest 0.01
√51 ≈ 7.14
Boundaries within which the roots are located
If the initial number belongs to the interval [1; 100], then the square root of this initial number will belong to the interval [1; 10].
For example, let the initial number be 64. This number belongs to the interval [1; 100]. Immediately we conclude that the square root of the number 64 will belong to the interval [1; 10]. Now remember the multiplication table. What multiplication of two identical factors results in 64? Clearly, the multiplication of 8 × 8, which is 82 = 64. So the square root of 64 is 8.
Example 1. Extract the square root of 49
The number 49 belongs to the interval [1; 100]. So the square root belongs to the interval [1; 10]. This root is number 7, because 72 = 49
√49 = 7
Example 2. Extract the square root of number 1
The number 1 belongs to the interval [1; 100]. So the square root belongs to the interval [1; 10]. This root is number 1, because 12 = 1
√1 = 1
Example 3. Extract the square root of 100
The number 100 belongs to the interval [1; 100]. So the square root belongs to the interval [1; 10]. The square root is 10, since 102 = 100
√100 = 10
It is clear that the interval [1; 100] also contains numbers from which square roots cannot be extracted. For such numbers the root must be extracted approximately. However, the approximate root will also be within the interval [1; 10].
For example, extract the square root of the number 37. There is no integer whose second power equals 37. Therefore, the extraction of the square root must be approximated. Extract it to the nearest hundredth:
√37 ≈ 6.08
To make it easier, you can find the nearest smaller number from which the root is extracted. This in this example was the number 36. The square root of it is 6. Then, starting from number 6, we can find an approximate value of the root √37 by checking various decimal fractions whose integer part is 6.
The squares of numbers from 1 to 10 must be known by heart. Below are these squares:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
And inversely, one should know the values of the square roots of these squares:
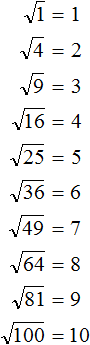
If you add a zero (or several zeros) to any number from 1 to 10 and then raise it to the second power, the resulting number will have twice as many zeros.
For example, 62 = 36. Add one zero to number 6 to get 60. Take 60 to the second power to get 3600.
602 = 3600
And if you add two zeros to the number 6 and raise it to the second power, you get a number with four zeros. That is, twice as many zeroes:
6002 = 360000
Then the following conclusion can be drawn:
If the original number contains a square and an even number of zeros, you can extract the square root of that number. To do this, extract the square root from the square we know and then write half the number of zeroes from the original number.
For example, extract the square root of the number 900. We see that this number has the familiar square 9. Extract the square root from it, and we get 3
Now from the original number write half of the number of zeros. The original number 900 contains two zeros. Half of this number of zeroes is one zero. Write it in the answer after number 3
Example 2. Extract the square root of 90000
Here again we have the familiar square 9 and an even number of zeros. Extract the root of 9 and write down half of the number of zeroes. The original number contains four zeros. Half of this number of zeroes is two zeroes:
Example 3. Extract the square root of 36000000
Here we have the familiar square 36 and an even number of zeros. Extract the root from the number 36 and write down half of the number of zeroes. The original number has six zeros. The half is three zeros:
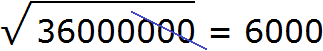
Example 4. Extract the square root of 2500
Here we have the familiar square 25 and an even number of zeros. Extract the root from the number 25 and write down half of the number of zeros. The original number has two zeros. The half is one zero:
If the sub-root number is increased (or decreased) by 100, 10000, then the root will increase (or decrease) by a factor of 10, 100, respectively.
For example, 
. If we increase the sub-root number by a factor of 100, the square root will increase by a factor of 10:
Conversely, if in equality we reduce the sub-root number by a factor of 100, then the square root will decrease by a factor of 10:
Example 2. Increase the sub-root number in Equality 
by 10000, then the square root of 70 will increase by a factor of 100
Example 3. Reduce the sub-root number of by a factor of 100, then the square root of 70 will decrease by a factor of 10.
This pattern allows you to extract the square root of a decimal if the fraction in question contains two digits after the dot, and those two digits form the familiar square. In such cases, multiply the given decimal by 100. Then take the square root of the resulting number and reduce the sub-root number by one hundred times.
For example, extract the square root of the number 0.25. This decimal has two digits after the dot and these two digits form the familiar square 25.
Multiply the decimal 0.25 by 100 to get 25. And the square root of 25 is easy to extract:
But we originally needed to extract the root of 0.25, not 25. To correct the situation, we return our decimal. If we decrease the sub-root number by a factor of 100, we will get 0.25 under the root and the answer will be decreased by a factor of 10:
Usually in such cases, it is enough to be able to move the point. Because moving a number's point to the right by two digits is like multiplying that number by 100.
In the previous example, you could move the dot to the right by two digits in the subordinate number 0.25, but in the resulting answer, you could move it to the left by one digit.
For example, extract the root of the number 0.81. We mentally move the point to the right by two digits, we get 81. Now take the square root of 81 and get 9. In answer 9, move the dot to the left by one digit, we get 0.9. So, 
.
This rule also works in a situation where the point is followed by four digits and these digits form the familiar square.
For example, the decimal 0.1225 contains four digits after the point. These four digits form the number 1225, the square root of which is 35.
Then we can extract the square root of 0.1225. Multiply this decimal by 10000 to get 1225. The square root of 1225 can be extracted using the square table:
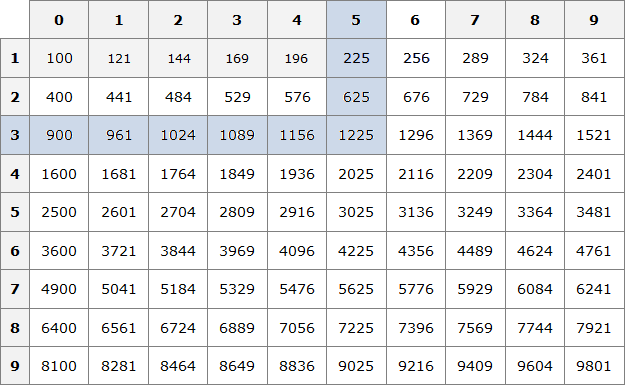
But we originally needed to extract the root from 0.1225, not from 1225. To correct the situation, we decrease the sub-root number in equality by a factor of 10000. As a result, the decimal 0.1225 is formed under the root, and the right part is reduced by a factor of 100
The same pattern will work for extracting roots from fractions like 12.25. If the digits that make up a decimal form the familiar square, with an even number of digits after the decimal, we can extract the root from the decimal.
Multiply the decimal 12.25 by 100 to get 1225. Extract the root of 1225
Now in equality reduce the sub-root number by a factor of 100. As a result, the number under the root is 12.25, and, accordingly, the answer is reduced by a factor of 10.
If the initial number belongs to the interval [100; 10000], then the square root of this initial number will belong to the interval [10; 100].
In this case the table of squares is applied:
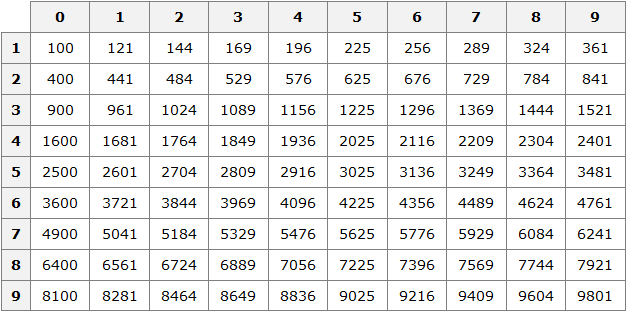
For example, let the initial number be 576. This number belongs to the interval [100; 10000]. We immediately conclude that the square root of 576 belongs to the range [10; 100]. Now open the table of squares and see what number in the second power equals 576
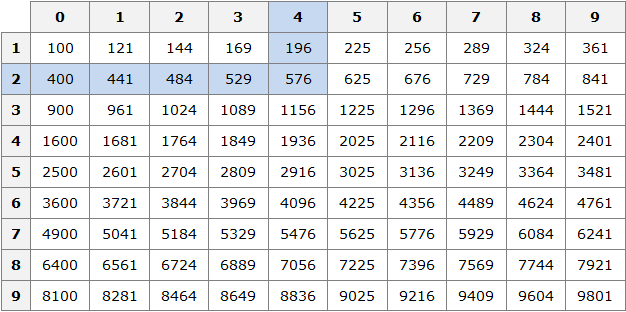
We see that this number is 24. So 
.
Example 2. Extract the square root of 432.
The number 432 belongs to the interval [100; 10000]. So the square root should be searched for in the interval [10; 100]. Open the table of squares and see what number in the second power equals 432. We find that number 432 is not in the table of squares. In this case, the square root must be searched approximately.
Extract the square root of 432 to the nearest tenth.
In the table of squares, the closest number to 432 is 400. The square root of it is 20. Starting from the number 20, we will check various decimal whose integer part is 20.
Let's check, for example, the number 20.8. To do this, let's square it:
20.82 = 432.64
The result is 432.64, which exceeds the original number 432 by 0.64. We see that the value 20.8 is large for the root √432. Let us check then the value 20.7
20.72 = 428.49
The value 20.7 is suitable as the root, because squaring this number results in the number 428.49, which is less than the original number 432, but close to it. So √432 ≈ 20.7
It is not necessary to memorize the intervals to find out in which boundaries the root is located. You can use the method of finding the nearest squares with an even number of zeros at the end.
For example, extract the root of the number 4225. We know the nearest least square of 3600, and the nearest larger square of 4900
3600 < 4225 < 4900
Extract the square roots from the numbers 3600 and 4900. These are numbers 60 and 70, respectively:
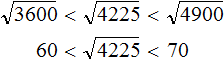
Then you can see that the square root of 4225 is between 60 and 70. You can even find it by a search method. Roots 60 and 70 are excluded at once, since they are the roots of numbers 3600 and 4900. Then you can check, for example, the root 64. Square it (or multiply this number by itself)
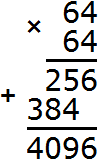
Root 64 is no good. Let's check root 65
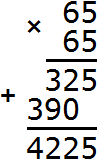
It turns out to be 4225. So 65 is the root of 4225.
Identical transformations with square roots
Various identity transformations can be performed on square roots, thereby facilitating their computation. Let us consider some of these transformations.
The square root of the product
The square root of the product is an expression of the form 
, where a and b are some numbers.
For example, the expression 
is the square root of the product of 4 and 9.
To extract such a square root, you must separately extract the square roots of the factors 4 and 9, presenting expression as the product of the roots 
. If we calculate these roots separately we obtain a product of 2 × 3, which is 6
Of course, you can avoid such manipulation and first calculate the sub-root expression 4 × 9, which is equal to 36. Then extract the square root of 36
But in extracting square roots from large numbers, this rule can be very useful.
Suppose you want to extract the square root of 144. This root is easily determined using the table of squares - it is equal to 12
But let's imagine that there is no table of squares at hand. In this case the number 144 can be decomposed into prime factors. Then from these prime factors make up the numbers from which the square roots are extracted.
So, let's decompose the number 144 into prime factors:
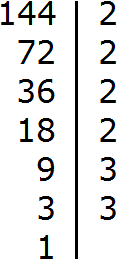
We obtained the following decomposition:
The expansion contains four twos and two threes. All the numbers in the expansion are multiplied. This makes it possible to represent the products of identical factors as a power with exponent 2.
Then the four twos can be replaced by the entry 22 × 22, and the two threes can be replaced by 32
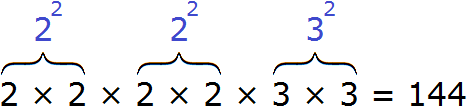
As a result, we will have the following decomposition:
Now you can extract the square root of the decomposition of 144
Apply the rule of extraction of the square root of the product:
It was said earlier that if a sub-root expression is raised to the second power, then that square root is equal to the modulus of the sub-root expression.
Then you get the product 2 × 2 × 3, which is 12
Simple factors are presented as a power for convenience and short writing. It is also allowed to write them under the root as they are, so that later multiplying them will give new factors.
Thus, by decomposing 144 into prime factors, we obtain the decomposition 2 × 2 × 2 × 2 × 3 × 3. This decomposition can be written under the root as it is:
then multiply some of the factors so that the square roots are extracted. In this case, you can multiply two twos twice and multiply two threes once:
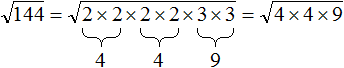
Then apply the rule of extraction of the square root of the product and get the final answer:
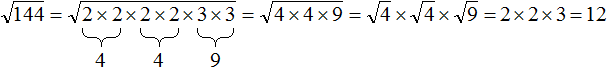
You can use the square root extraction rule to extract the square root from a product and other large numbers. This includes numbers that are not in the square table.
For example, extract the square root of number 13456. This number is not in the table of squares, so we will use the rule of extracting the square root of the product, having previously decomposed number 13456 into prime factors.
So, let's decompose the number 13456 into prime factors:
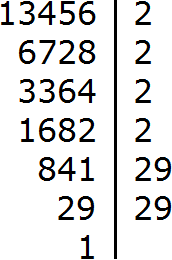
In the expansion there are four twos and two numbers 29. The twos are represented twice as 22. And the two numbers 29 are represented as 292. As a result, we obtain the following decomposition of 13456
Now we will extract the square root of the decomposition of 13456
So if a ≥ 0 and b ≥ 0, then 
. That is, the root of the product of non-negative factors is equal to the product of the roots of these factors.
Let us prove the equality of . To do this we will use the definition of the square root.
By definition, the square root of a is the number b at which the equality b2 = a is satisfied.
In our case, we need to make sure that the right-hand side of equality , when raised to the second power, will result in a sub-root expression of the left-hand side, that is, the expression ab.
So, write down the right-hand side of the equality and raise it to the second power:
Now let us use the rule of exponentiation of a product. According to this rule, each factor of a given product must be raised to a specified power:
It was said earlier that if an expression of the form is raised to the second power, we obtain a sub-root expression. Let us apply this rule. Then we obtain ab. This is the sub-root expression of the square root of 
It means that the equality is valid, because when you raise the right part to the second power, you get a sub-root expression of the left part.
The rule for extracting the square root from a product also works if there are more than two factor under the root. That is, the following equation is valid:
, when a ≥ 0 and b ≥ 0, c ≥ 0.
Example 1. Find the value of the square root 
Write the root as a product of roots, extract them, and then find the value of the product:
Example 2. Find the value of the square root 
Let's represent the number 250 as a product of 25 and 10. We will do this under the root sign:
Now there are two identical factors 10 and 10 under the root. Multiply them and you get 100
Then we apply the rule of extraction of the square root of the product and get the final answer:
Example 3. Find the value of the square root 
Let us use the rule of increasing the power to a power. Let us represent the power of 114 as (112)2.
Now use the rule of extracting the square root from the square of a number:
In our case, the square root of (112)2 will be 112. Simply put, the outer exponent of power 2 will disappear, but the inner exponent will remain:
Then we raise the number 11 to the second power and get the final answer:
This example can also be solved using the rule of extraction of the square root of the product. To do this, write the sub-root expression 114 as product 112 × 112. Then extract the square root of that product:
Example 4. Find the value of the square root 
Let us rewrite power 34 in the form (32)2, and power 56 in the form (53)2
Then we use the rule of extraction of the square root of the product:
Next, use the rule of extraction of the square root from the square of a number:
Calculate the product of the resulting powers and get the final answer:
The factors below the root can be decimals. For example, extract the square root of the product 
Write the root of as a product of roots, extract them, then find the value of the resulting product:
Example 6. Find the value of the square root 
Example 7. Find the value of the square root 
If the first factor is multiplied by the number n and the second factor is divided by that number n, then the product will not change.
For example, the product of 8 × 4 is 32
8 × 4 = 32
Multiply the factor 8 by, say, number 2, and divide the factor 4 by the same number 2. Then you get the product 16 × 2, which also equals 32.
(8 × 2) × (4 : 2) = 32
This property is useful in solving some square root extraction tasks. The factors of a sub-root expression can be multiplied and divided so that the roots are extracted from them.
For example, extract the square root of the product 
. If you immediately use the rule for extracting a square root from a product, you cannot extract the roots √1.6 and √90, because they are not extractable.
Analyzing the sub-root expression 1.6 × 90, we can see that if the first factor 1.6 is multiplied by 10 and the second factor 90 is divided by 10, then the product is 16 × 9. From such a product the square root can be extracted using the rule of extraction of the square root from the product.
Let us write down the complete solution of this example:
The multiplication and division process can be done in your mind. You can also skip the detailed notation of extracting the square root of each quotient. Then the solution becomes shorter:
Example 9. Find the value of the square root 
Multiply the first factor by 10 and divide the second by 10. Then the product 36 × 0.04 is formed under the root, from which the square root is extracted:
If you swap the left and right parts of equality , you get equality 
. This transformation allows you to simplify the calculation of some roots.
For example, find out what the value of the expression 
.
No square roots can be extracted from the numbers 10 and 40. Let us use the rule, that is, replace the expression of two roots with an expression with one root, under which will be the product of the numbers 10 and 40
Now find the value of the product under the root:
And the square root of the number 400 is extracted. It is equal to 20
The factors below the root can be expanded into factors, grouped, represented as a power, and multiplied to obtain new factors from which the roots are extracted.
For example, find the value of expression 
.
Let's use the rule
The factor 32 is 25. Let's represent this factor as 2 × 24
Multiply the factors 2 and 2 to obtain 4. And let's represent the factor 24 as a power with index 2
Now let's use rule and calculate the final answer:
Example 12. Find the value of expression 
Let's use rule
The factor 8 is 2 × 2 × 2, and the factor 98 is 2 × 7 × 7.
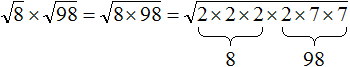
Now there are four twos and two sevens under the root. Four twos can be written as 22 × 22, and two sevens as 72
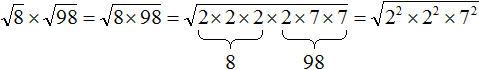
Now let's use rule and calculate the final answer:
The square root of a fraction
The square root of 
is a fraction whose numerator is the square root of a and whose denominator is the square root of b.
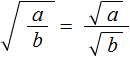
For example, the square root of a fraction 
is a fraction whose numerator is the square root of 4 and whose denominator is the square root of 9.
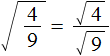
Calculate the square roots in the numerator and denominator:
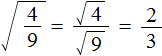
So the square root of fraction is 
.
Let us prove that equality 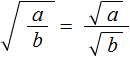is true.
Let's raise the right part to the second power. If the result is a fraction of 
, it means that equality 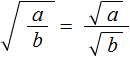is true:
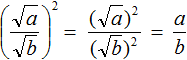
Example 1. Extract the square root of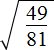 
Use the rule of extraction of the square root of a fraction:
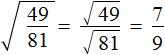
Example 2. Extract the square root of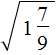 
Convert the sub-root expression into an irregular fraction, then use the rule of extraction of the square root of the fraction:
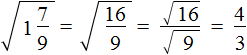
Example 3. Extract the square root of 
The square root of 0.09 is 0.3. But it is possible to extract this root using the rule of extraction of the square root from a fraction.
Let's represent the sub-root expression as fraction. 0.09 is nine hundredths:
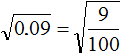
Now you can use the rule of extraction of the square root of a fraction:
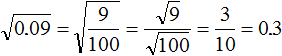
Example 4. Find the value of the expression 
Extract the roots of 0.09 and 0.25, then add up the results:
You can also use the rule of extraction of the square root of a fraction:
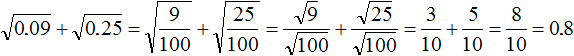
In this example, the first method was easier and more convenient.
Example 5. Find the value of the expression 
First calculate the square root, then multiply it with 10. Subtract the result from 4.
Example 6. Find the value of the expression 
First, find the value of the square root of 
. It is 0.6 since 0.62 = 0.36
Now let's calculate the resulting expression. According to the order of operations, we must first perform multiplication, then addition:
Factoring out from under the root sign
In some tasks it may be useful to take the factor out from under the sign of the root.
Consider the square root of product 
. According to the rule of extraction of the square root of product, you must extract the square root from each factor of the product:
In our example, the square root is extracted only from a factor 4. We extract it and leave expression 
unchanged:
This is factoring out from under the root sign.
In practice, a sub-root expression most often needs to be decomposed into factors.
Example 2. Take the factor out from under the sign of the root in expression 
Decompose the sub-root expression into the factors 9 and 2. Then we obtain:
Now use the rule of extraction of the square root of the product. Only the root of factor 9 can be extracted. Leave factor 2 under the root:
Example 3. Take the factor out from under the sign of the root in expression 
Decompose the sub-root expression into the factors 121 and 3. Then we obtain:
Now use the rule of extraction of the square root of the product. Only the root of the factor 121 can be extracted. Leave the expression √3 under the root:
Example 4. Take the factor out from under the sign of the root in expression 
Use the rule of extraction of the square root of the product:
The square root is extracted only from number 121. Extract it, and leave the expression √15 unchanged:
It turns out that factor 11 is taken out from under the sign of the root. It is customary to write the removed factor before the expression with the root. Swap the expressions √15 and 11:
Example 5. Take the factor out from under the sign of the root in expression 
Decompose the sub-root expression into the factors 4 and 3
Use the rule of extraction of the square root of the product:
Extract the root from number 4 and leave the expression √3 unchanged:
Example 6. Simplify the expression 
Let's represent the second summand 
as 
. And the third summand 
can be represented as 
Now, in expressions 
and , take the factor out from under the root sign:
In the second summand 
, multiply the numbers -4 and 4. Let's rewrite the rest of the summand unchanged:
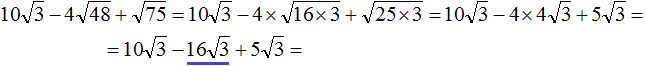
Note that the square root of √3 is a common multiplier in the resulting expression. Take it out of brackets:
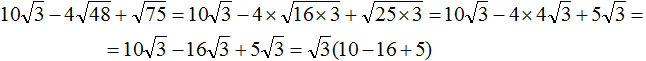
Calculate the contents of the brackets, we get -1
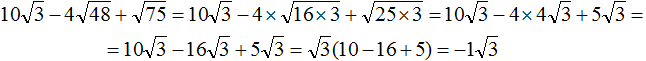
If the multiplier is -1, only the minus is written down. The one is omitted. The final answer is then -√3
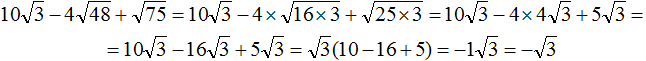
Put a factor under the sign of the root
Consider the following expression:
In this expression, number 5 is multiplied by the square root of number 9. Find the value of this expression.
First extract the square root, then multiply it with the number 5.
The square root of 9 is 3. Multiply it with the number 5. Then we get 15
The number 5 in this case was the factor. Let's put this factor under the root sign. But we need to do this in such a way that the value of the original expression will not change as a result of our actions. To put it simply, after putting the factor 5 under the root sign, the resulting expression should still be 15.
The value of the expression will not change if number 5 is raised to the second power and only then put it under the root:
So, if the expression 
is given and you want to put the factor a under the sign of the root, then you must raise the factor a to the second power and put it under the root:
Example 1. Put a factor under the root sign of the expression 
Raise the number 7 to the second power and put it under the root sign:
Example 2. Put a factor under the root sign of the expression 
Raise the number 10 to the second power and put it under the root sign:
Example 3. Put a factor under the root sign of the expression 
You can only put a positive factor under the sign of the root. It was said earlier that an expression of the form makes no sense.
However, if there is a negative factor before the root sign, then the minus can be left behind the root sign and the number itself can be put under the root sign.
Example 4. Put a factor under the root sign of the expression 
In this example, only 3 is put under the root sign. The minus remains behind the root sign:
Example 5. Perform exponentiation in the following expression:
Use the formula for the square of the sum of two expressions:
(a + b)2 = a2 + 2ab + b2
The variable a in this case is √3, and the variable b is √2:
Now we need to simplify the resulting expression.
For expressions 
and 
we will apply rule 
. Earlier we said that if an expression of the form is raised to the second power, then this expression is equal to sub-root expression a.
And in expression 
for factors and 
we apply rule . That is, replace the product of the roots by one common root:
Let us give like terms. In this case we can add the terms 3 and 2. And in the term 
calculate the product that is under the root:
Tasks for independent decision
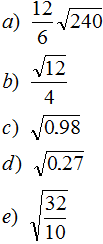
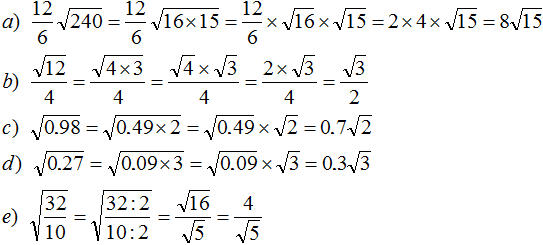
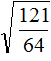
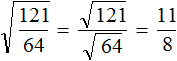
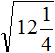
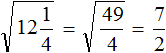
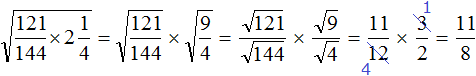
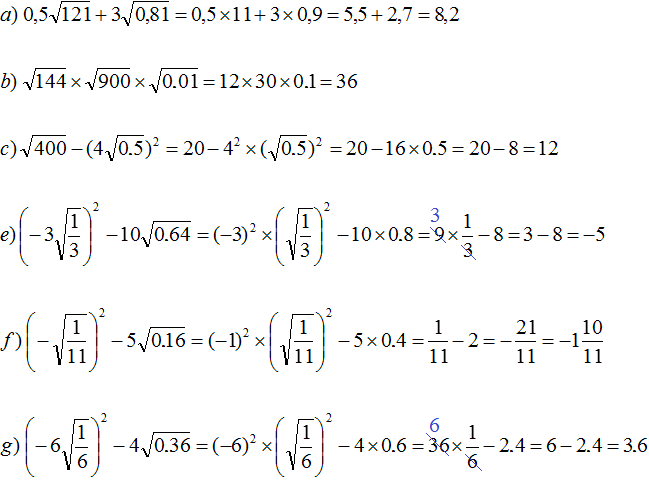
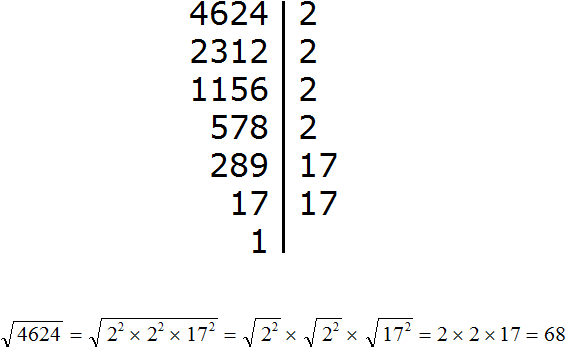
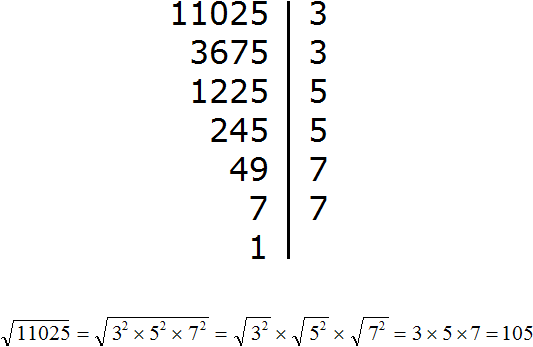
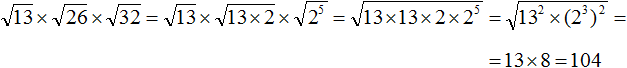
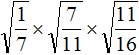
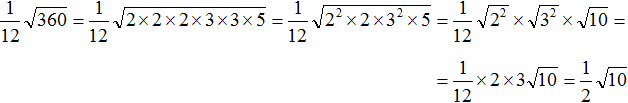
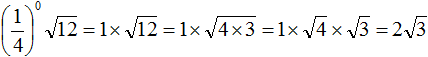
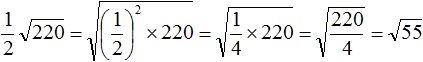
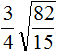
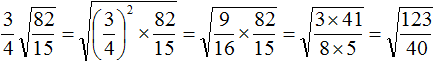
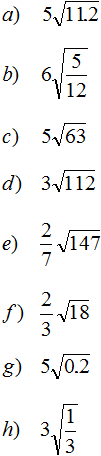
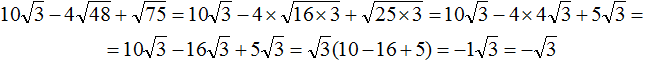
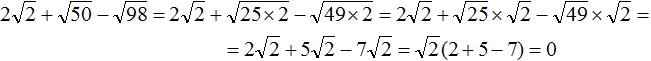
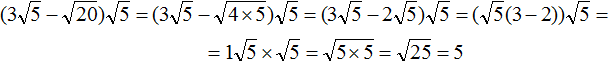
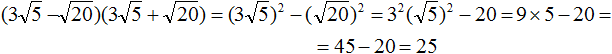
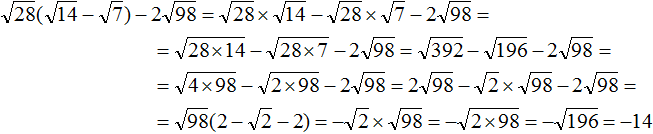
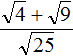
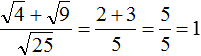
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.