Decimal have a wide range of applications. They are used in economics, medicine, engineering, and many other fields. In this lesson we will look at some basic operations that may be useful in the future.
Comparing decimals
To compare two decimal, you need to make the number of digits after the dot the same in both decimals by adding zeros to one of them. Then discard the commas in both fractions and compare the resulting numbers.
For example, compare decimals 5.345 and 5.36.
The first fraction has three digits after the dot, and the second fraction has only two. You should add another zero at the end of the second fraction to make the number of digits after the dot in both fractions the same.
Add zero to the end of the second fraction, then we get fractions 5.345 and 5.360. Now we discard the points in both fractions and get 5345 and 5360. So we compare them like regular numbers. 5345 is less than 5360.
5345 < 5360
So the fraction 5.345 is smaller than the fraction 5.36
5.345 < 5.36
Example 2. Compare the decimals 6.782 and 6.71
Make the number of digits in both decimals the same:
6.782
6.710
Let's drop the dots:
6782
6710
6782 more than 6710
6782 > 6710
So the decimal 6.782 is larger than the decimal 6.71
6.782 > 6.71
Finding a fraction of a whole number
In previous lessons, we found a fraction from a whole number. To do this, we divided the number by the denominator of the fraction and multiplied the result by the numerator of the fraction.
For example, to find 
of a number 9, divide the number 9 by the denominator of the fraction and multiply the result by the numerator of the same fraction
9 : 3 = 3
3 × 2 = 6
So of 9 is 6.
But you can also find decimals from a number. Finding a decimal from a number is much easier. To find a decimal fraction of a number, just multiply the number by the fraction from yur task.
For example, find 0.5 of number 12. To find 0.5 of number 12, just multiply 12 by 0.5
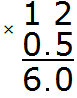
The answer is 6. So 0.5 of 12 is 6.
Let's check if we got 0.5 of 12 right. First, convert the decimal 0.5 to an ordinary fraction. 0.5 is zero point five. We do not write zero, but write five tenths at once:
Let's make this fraction simpler for our work. To do this, we reduce it by 5
We got a fraction of 
. Now we find of the number 12. It is not hard to guess that of 12 is 6. So the decimal 0.5 from number 12 was found correctly.
Example 2. Find 0.4 of one meter
One meter is 100 cm. To find 0.4 of 100 cm, multiply 100 cm by 0.4. And to multiply 100 cm by 0.4 you need to move the point to the right by two digits in 0.4:
100 × 0.4 = 40
So 0.4 of one meter is 40 cm.
A decimal can also be found from a decimal fraction. For example, let's find 0.5 from 2.5. To do this, multiply 2.5 by 0.5
2.5 × 0.5 = 1,25
Finding a whole number by its decimal fraction
In previous lessons, we found a whole number by its fraction. To find the whole number by its fraction, we divided the known number by the numerator of the fraction and multiplied the result by the denominator of the fraction.
For example, if 
of a number is 6, then to find the whole number, divide 6 by 2 and multiply the result by 4.
6 : 2 = 3
3 × 4 = 12
So if the whole number is 12.
You can also find a number by its decimal. Finding a number by its decimal is much easier. To find a number by its decimal, simply divide the number by the given fraction.
Example 1. 0.6 of the whole number is 12, find the whole number. To find the whole number, simply divide 12 by 0.6
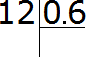
To divide 12 by 0.6, move the point to the right by one digit in the divisor and in the divisor. Then we get the expression 120 : 6. This expression is easy to calculate:
120 : 6 = 20
So if 0.6 of the whole number is 12, then the whole number is 20.
Example 2. A cyclist has traveled 3 km, which is 0.2 of the total distance the cyclist must travel. How much distance does the cyclist have to travel?
If 0.2 of the total distance is 3 km, then in order to find the total distance, divide 3 by 0.2. To divide 3 by 0.2, move the point to the right by one digit in the divisor and in the divisor. Then we get the expression 30 : 2. This expression is easy to calculate:
30 : 2 = 15
So the entire distance that the cyclist has to travel is 15 km.
Comments