Negative numbers are numbers with a minus (-) sign, e.g. -1, -2, -3. Read as: minus one, minus two, minus three.
An example of the use of negative numbers is a thermometer that shows the temperature of the body, air, soil, or water. In winter, when it is very cold outside, the temperature is negative (or as they say popularly "degrees below zero").
For example, it is -10 degrees below zero:
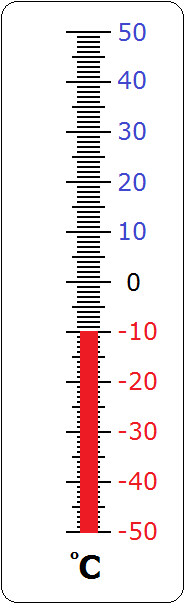
The usual numbers we looked at earlier, such as 1, 2, and 3, are called positive numbers. Positive numbers are numbers with a plus sign (+).
When writing the positive numbers we do not write the + sign, so we see the usual numbers we are used to: 1, 2, 3. But keep in mind that these positive numbers look like this: +1, +2, +3.
Number line
A number line (The simplest example of a coordinate system) is a straight line on which all numbers are placed: both negative and positive. It looks like this:
![]()
Only numbers from -5 to 5 are shown here. In fact, the number line is infinite. The figure shows only a small fragment of it.
Numbers on the coordinate line are marked as dots. In the figure, the bold black arbitrary point is the origin. Negative numbers are placed to the left of the origin, and positive numbers are placed to the right.
A number line goes infinitely on both sides. Infinity in mathematics is denoted by the symbol ∞. The negative direction will be denoted by the symbol -∞, and the positive direction by the symbol +∞. Then we can say that the number line contains all numbers from minus infinity to plus infinity:
(−∞; +∞)
Each point on a number line has its own name and coordinate. The name is any Latin letter. A coordinate is a number that shows the position of a point on that line. Simply put, a coordinate is the very number that we want to mark on the coordinate line.
For example, point A(2) reads "point A with coordinate 2" and will be indicated on the coordinate line as follows:
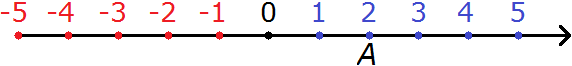
Here A is the name of the point, 2 is the coordinate of point A.
Example 2. Point B(4) reads "point B with coordinate 4" and will be denoted on the coordinate line as follows:

Here B is the name of the point, and 4 is the coordinate of point B.
Example 3. Point M(-3) reads "point M with coordinate minus three" and will be denoted on the coordinate line as follows:
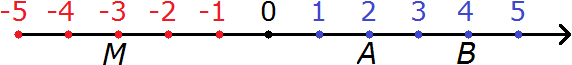
Here M is the name of the point, -3 is the coordinate of point M.
Points can be named by any letters. But it is generally accepted to designate them with capital Latin letters. Moreover, the beginning of the number line, otherwise called the origin, is commonly denoted by the capital Latin letter O
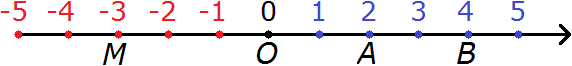
It is easy to see that negative numbers lie to the left relative to the origin and positive numbers to the right.
With each step to the left, the number will decrease.
And with each step to the right, the number will increase.
An arrow pointing to the right indicates a positive direction of counting.
Comparing Negative and Positive numbers
Rule 1: Any negative number is smaller than any positive number.
For example, compare two numbers: −5 and 3. Minus five is less than three, despite the fact that five catches the eye first as a number larger than three.
This is because -5 is a negative number and 3 is a positive number. On the number line you can see where the numbers -5 and 3 are located

You can see that -5 is to the left and 3 is to the right. And we said that "if one number is to the left of another, it is smaller". And the rule says that any negative number is smaller than any positive number. It follows that
−5 < 3
«Minus five is less than three»
Rule 2: Of the two negative numbers, the one to the left of the coordinate line is smaller.
For example, compare the numbers -4 and -1.
Minus four is less than minus one.
This is again due to the fact that on the number line -4 is more to the left than -1
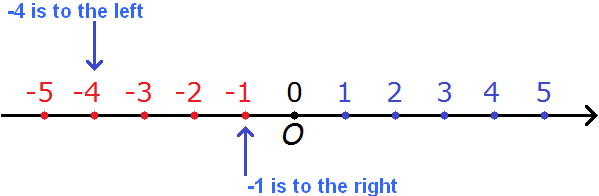
You can see that -4 lies to the left and -1 to the right. And we said that "if one number is to the left of another, it is smaller". And the rule says that of two negative numbers the smaller is the one which is to the left of the coordinate line. So it follows that
−4 < −1
Minus four is less than minus one
Rule 3. Zero is greater than any negative number.
For example, compare 0 and -3.
Zero is greater than minus three. This is because on the coordinate line 0 is more to the right than -3.
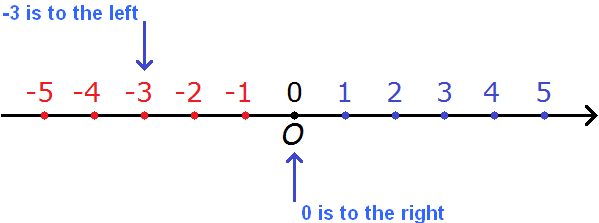
You can see that 0 is to the right and -3 is to the left. And we said that "numbers farther to the right on the number line are greater". And the rule says that zero is greater than any negative number. It follows that
0 > −3
Zero is greater than minus three
Rule 4: Zero is less than any positive number.
For example, compare 0 and 4.
Zero is less than 4. This is clear as it is. But we will try to prove it by looking at the number line:
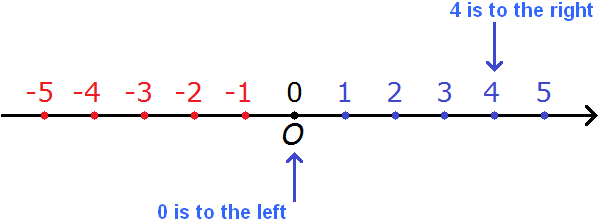
You can see that on the coordinate line 0 is on the left and 4 is on the right. And we said that "numbers farther to the left on the number line are smaller". And the rule says that zero is smaller than any positive number. Hence it follows that
0 < 4
Zero is less than four
Comments