Factoring Trinomials The Easy Fast Way
A quadratic trinomial is a polynomial of the form ax2 + bx + c.
In past lessons, we solved quadratic equations. The general view of such equations was as follows:
ax2 + bx + c = 0
The left side of this equation is a quadratic trinomial.
One of the useful transformations in solving problems is to decompose a quadratic trinomial into multipliers. To do this, the original quadratic trinomial is equated to zero and the quadratic equation is solved. In this case it is said that the roots of the quadratic trinomial are found.
The resulting roots x1 and x2 should be put into the following expression, which will be the decomposition:
a(x β x1)(x β x2)
Thus, in order to decompose a quadratic trinomial into multipliers by solving a quadratic equation, you must use the following ready-made formula:
ax2 + bx + c = a(x β x1)(x β x2)
Where the left part is the original quadratic trinomial.
Example 1. Decompose the following quadratic trinomial into multipliers:
x2 β 8x + 12
Find the roots of the quadratic trinomial. To do this, equate this quadratic trinomial to zero and solve the quadratic equation:
x2 β 8x + 12 = 0
In this case the coefficient b is even. Therefore we can use the formulas for the even second coefficient. To save time, some detailed calculations can be skipped:
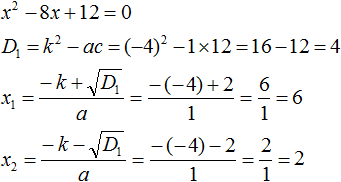
So x1 = 6, x2 = 2. Now use the formula ax2 + bx + c = a(x β x1)(x β x2). Instead of ax2 + bx + c on the left, we write our square trinomial x2 β 8x + 12. On the right, we substitute the values we have. In this case a = 1, x1 = 6, x2 = 2
x2 β 8x + 12 = 1(x β 6)(x β 2) = (x β 6)(x β 2)
If a equals one (as in this example), the solution can be written in a shorter form:
x2 β 8x + 12 = (x β 6)(x β 2)
To check if the quadratic trinomial is correctly decomposed into multipliers, open the brackets on the right side of the resulting equality.
Open the brackets on the right side of the equality, that is, in the expression (x - 6)(x - 2). If we have done everything correctly, we should get the quadratic trinomial x2 β 8x + 12
(x β 6)(x β 2) = x2 β 6x β 2x + 12 = x2 β 8x + 12
Example 2. Decompose the following quadratic trinomial into multipliers:
2x2 β 14x + 24
Equate this quadratic trinomial to zero and solve the equation:
2x2 β 14x + 24 = 0
As in the last example, the coefficient b is even. Therefore we can use the formulas for the even second coefficient:
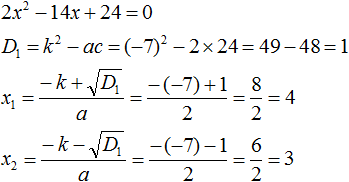
So x1 = 4, x2 = 3. Equate the quadratic trinomial 2x2 - 14x + 24 to the expression a(x β x1)(x β x2), where instead of variables a, x1 and x2 we substitute the corresponding values. In this case a = 2
2x2 β 14x + 24 = 2(x β 4)(x β 3)
Let's check it. To do this, open the brackets on the right side of the resulting equality. If we have done everything correctly, we should get a quadratic trinomial 2x2 - 14x + 24
2(x β 4)(x β 3) = 2(x2 β 4x β3x + 12) = 2(x2 β 7x + 12) = 2x2 β 14x + 24
How it works
The decomposition of a quadratic trinomial into multipliers occurs if instead of the coefficients of the quadratic trinomial we put Viet's theorem and perform identical transformations.
First, consider the case where the coefficient a of a quadratic trinomial is equal to one:
x2 + bx + c
Recall that if a quadratic equation is a reduced equation, then Viet's theorem has the form:
Then the given quadratic trinomial x2 + bx + c can be decomposed as follows. First express b from the equation x1 + x2 = βb. To do this, we can multiply both parts of it by -1
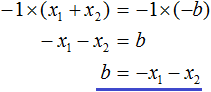
Variable c from Viette's theorem does not need to be expressed - it is already expressed. It is enough to swap the left and the right parts:
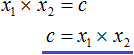
Now substitute the expressed variables b and c in the quadratic trinomial x2 + bx + c
Open brackets where you can:
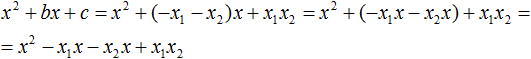
In the resulting expression, decompose the polynomial into factors by grouping. In this case it is convenient to group the first term with the second, and the third with the fourth:
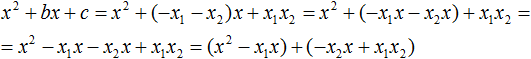
Take the common factor x1 out of the first brackets and the common factor -x2 out of the second brackets.
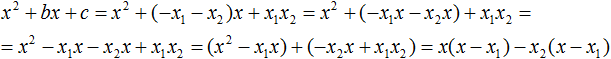
Then we notice that the expression (x - x1) is a common multiplier. Take it out of the brackets:
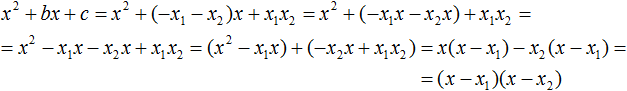
We came to the conclusion that the expression x2 + bx + c became equal to (x β x1)(x β x2)
x2 + bx + c = (x β x1)(x β x2)
But this was the case when the original quadratic trinomial is a reduced trinomial. In it the coefficient a is equal to one. So in the expansion formula of such a quadratic trinomial the coefficient a can be omitted.
Now consider the case when the coefficient a of a quadratic trinomial is not equal to one. This is exactly the case when in the expansion formula there is the coefficient a before the brackets.
ax2 + bx + c = a(x β x1)(x β x2)
Recall that if a quadratic equation is not reduced, that is, it has the form ax2 + bx + c = 0, then Viet's theorem takes the following form:
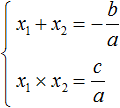
This is because Viet's theorem only works for reduced quadratic equations. And for the equation ax2 + bx + c = 0 to become a reduced equation, you have to divide both parts of it by a
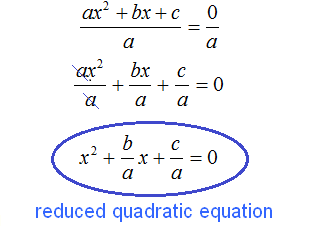
Next, in order to decompose the quadratic trinomial of the form ax2 + bx + c into multipliers, we substitute the corresponding expressions from Viet's theorem instead of b and c. But this time we should use equations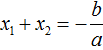 
and 
First, let us express b and c. In the first equality multiply both parts by a. Then multiply both parts of the resulting equality by -1
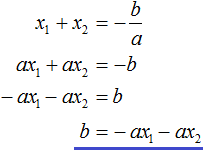
Now express c from the second equality. To do this, multiply both parts of it by a
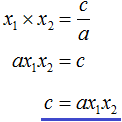
Now substitute the expressed variables b and c into the quadratic trinomial ax2 + bx + c. For clarity, we will perform each transformation on a new line:
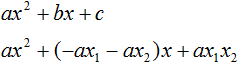
Here instead of variables b and c we substituted the expressions βax1 β ax2 and ax1x2, which we expressed earlier from Viet's theorem. Now let us open the brackets where it is possible:
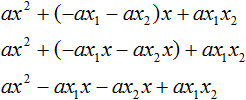
In the resulting expression, decompose the polynomial into factors by grouping. In this case it is convenient to group the first term with the second, and the third with the fourth:
Now take the common factor ax out of the first brackets and the common factor βax2 out of the second brackets
Then we notice that the expression x - x1 is also a common multiplier. Take it out of the brackets:
The second brackets contain the common factor a. Take it out of the brackets. It can be placed at the beginning of the expression:
We came to the conclusion that the expression ax2 + bx + c became equal to a(x β x1)(x β x2)
ax2 + bx + c = a(x β x1)(x β x2)
Note that if a quadratic trinomial has no roots, then it cannot be decomposed into multipliers. Indeed, if no roots of the quadratic trinomial are found, then there will be nothing to substitute in the expression a(x β x1)(x β x2) instead of the variables x1 and x2.
If a quadratic trinomial has only one root, then that root is simultaneously substituted in x1 and x2. For example, the quadratic trinomial x2 + 4x + 4 has only one root -2
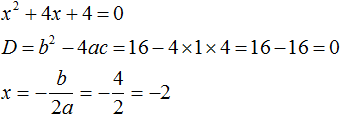
Then the value -2 will be substituted for x1 and x2 in the factorization process. And the value of a in this case is equal to one. You can not write it down, because it will not give anything:
The brackets inside the brackets can be opened. Then we get the following:
If a short answer is needed, the last expression can be written as (x + 2)2 because (x + 2)(x + 2) is a multiplication of two factors, each of which is equal to (x + 2)
Examples of decompositions
Example 1. Decompose the following quadratic trinomial into multipliers:
3x2 β 2x β 1
Find the roots of the quadratic trinomial:
Let's use the expansion formula. On the left side write the quadratic trinomial 3x2 β 2x β 1, and on the right side write its expansion in the form a(x β x1)(x β x2), where instead of a, x1 and x2 we substitute the corresponding values:
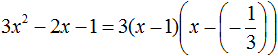
In the second brackets, you can replace subtraction with addition:
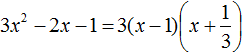
Example 2. Decompose the following quadratic trinomial into multipliers:
3 β 11x + 6x2
Arrange the terms so that the high coefficient is first, the middle coefficient is second, and the free member is third:
6x2 β 11x + 3
Find the roots of the quadratic trinomial:
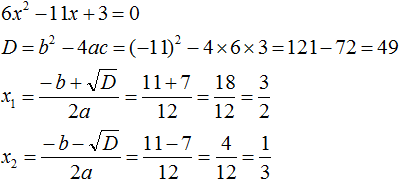
Let us use the decomposition formula:
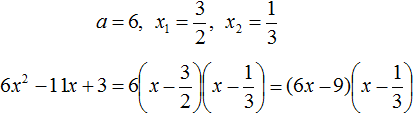
Let us simplify the resulting expansion. Take the common factor 3 out of the first brackets
Now let us use the Associative law of multiplication. Recall that it allows us to multiply the multipliers in any order. Multiply 3 by the second brackets. This will get rid of the fractions in these brackets:
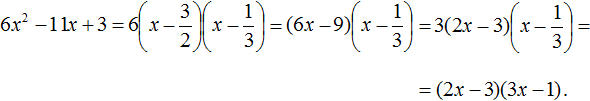
Example 3. Decompose the following quadratic trinomial into multipliers:
3x2 + 7x β 6
Find the roots of the quadratic trinomial:
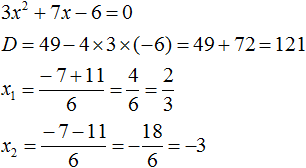
Let us use the decomposition formula:
Example 4. Find the value of k in which the factorization of the trinomial 3x2 β 8x + k contains the factor (x - 2)
If the expansion contains the factor (x - 2), then one of the roots of the quadratic trinomial is 2. Let root 2 be the value of the variable x1
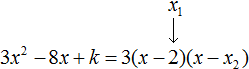
To find the value of k, we need to know what the second root equals. To find it, we will use Vyet's theorem.
In this case, the quadratic trinomial is not reduced, so the sum of its roots will be a fraction of 
, and the product of the roots will be a fraction of 
.
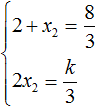
Express the variable x2 from the first equality and immediately substitute the found value into the second equality instead of x2
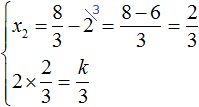
Now express k from the second equality. In this way we will find its value.
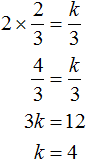
Example 5. Decompose the following quadratic trinomial into multipliers:
Let us rewrite this trinomial in a convenient form. If we replace division in the first term with multiplication, we obtain 
. If we swap the factors, we get 
. That is, the quotient of a becomes 
The coefficient b can be converted to a fraction. This makes it easier to look for the discriminant:
Find the roots of the quadratic trinomial:
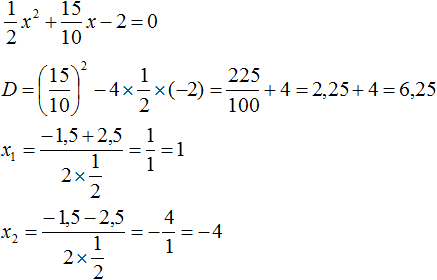
Let us use the decomposition formula:
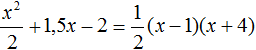
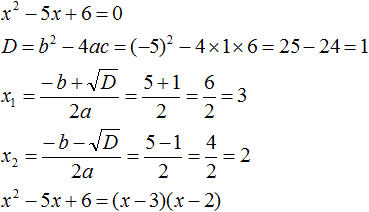
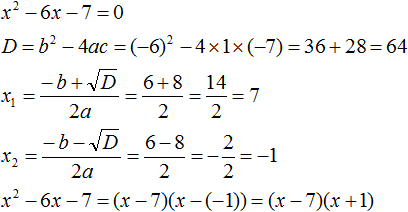
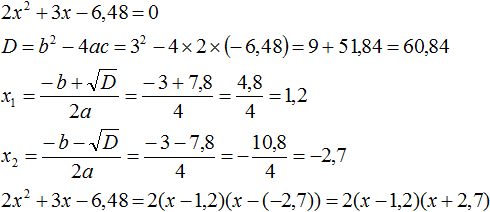
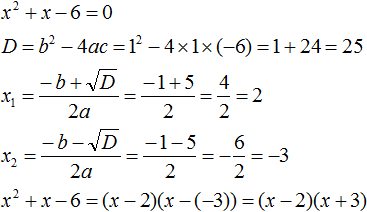
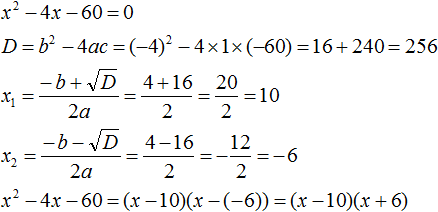
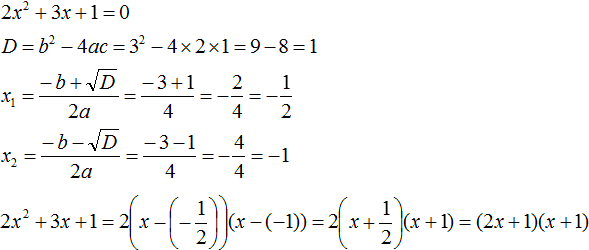
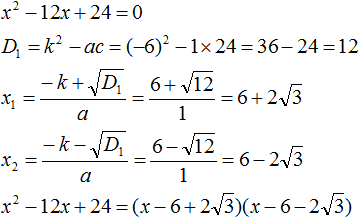
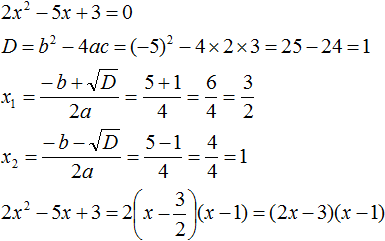
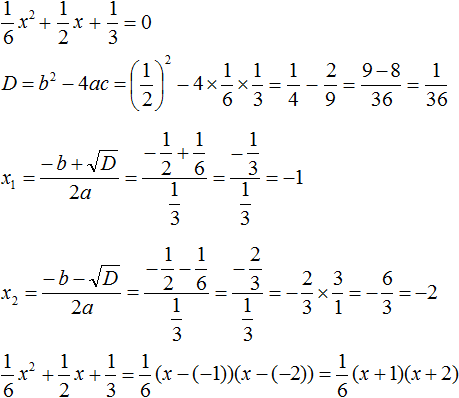
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.