Conversion of improper fractions to decimal

An improper fraction is a fraction with a numerator greater than the denominator.

There are improper fractions that have 10, 100, 1000 or 10000 in the denominator. Such fractions can be converted to decimals. However, before converting to a decimal, the whole part of the fraction must be extracted.

Example 1. Convert an improper fraction into a decimal.

Fraction is an improper fraction. To convert such a fraction into a decimal, you must first select the whole part of the fraction. Recall how to select the whole part of improper fractions. If you forget, we suggest that you go back to this topic and study it thoroughly.

So, let us distinguish the whole part in the improper fraction . Recall that a fraction means division, in this case dividing 112 by 10. The division must be done with a remainder:

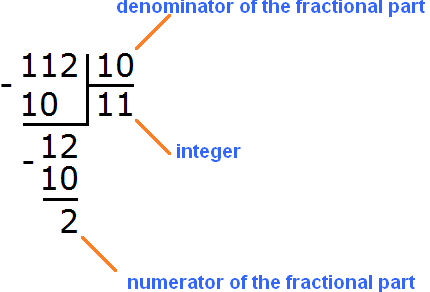
Let's look at this picture and assemble a new mixed number, like a children's construction set. The quotient 11 is the whole part, the remainder 2 is the numerator of the fractional part, and the divisor 10 is the denominator of the fractional part:

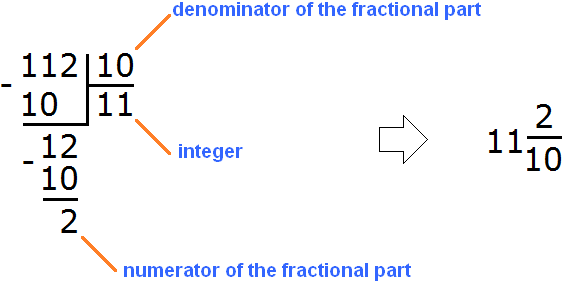
We got a mixed number of . We will convert it to a decimal. And we already know how to convert such numbers to decimals. First, we write down the whole part and put a dot:

11.

Now count the number of zeros in the denominator of the fractional part. We see that there is one zero. And there is one digit in the numerator of the fractional part. So the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part are the same. This allows us to write the numerator of the fractional part right after the point:

11.2

So the wrong fraction when converted to decimal converts to 11.2

The decimal 11.2 reads like this:

«Eleven point two-twenty».

Example 2. Convert an improper fraction into a decimal.

This is an incorrect fraction because the numerator is larger than the denominator. But it can be converted to a decimal because the denominator contains the number 100.

First of all, isolate the whole part of this fraction. To do this, divide 450 by 100:

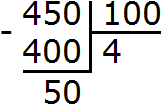
Let's put together a new mixed number - we get . Now convert it to a decimal. Write down the whole part and dot it:

4.

Now count the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part. We see that the number of zeros in the denominator and the number of digits in the numerator are the same. This allows us to write the numerator of the fractional part after the dot:

4.50

So the wrong fraction when converted to decimal converts to 4.50

When solving problems, if there are zeros at the end of a decimal, they can be discarded. Let's discard the zero in our answer, too. Then we get 4.5

This is one of the interesting features of decimals. It consists in the fact that zeros that stand at the end of the fraction do not give any weight to the fraction. In other words, the decimal 4.50 and 4.5 are equal and you can put an equal sign between them:

4.50 = 4.5

This begs the question, "Why is this the case?" After all, 4.50 and 4.5 look different fractions. The whole secret lies in the basic property of fractions, which we studied earlier. We will try to prove why the decimals 4.50 and 4.5 are equal, but after studying the next topic, which is called "converting a decimal to a mixed number".

Video lesson

Add comment