We continue to study the modulus of a number. Today we will learn how to solve inequalities with modulus.
To solve inequalities with modulus, you must first know how to solve the simplest linear inequalities, and know what modulus is and how to solve it.
Whether we are solving an equation or an inequality, we need to be able to solve the modulus.
Consider, for example, the simplest inequality with a module:
|x| > 2
To solve this inequality, expand the modulus.
If the submodular expression is greater than or equal to zero, then the original inequality will take the form:
x > 2
The solution of this inequality is the set of all numbers greater than 2. Mark them on the coordinate line:

And if the submodular expression is less than zero, then the initial inequality will take the form:
−x > 2
Multiply both parts of this inequality by -1. Then we obtain the inequality x < -2. The solution of this inequality is the set of all numbers smaller than -2. Mark these solutions in the same figure where we marked solutions to the inequality x > 2.

Funnily enough, the resulting intervals x < -2 and x > 2 are the answer to our problem. If we substitute in the original inequality |x| > 2 any value of x that satisfies this inequality, then this value will belong to the interval (-∞ ; -2) or the interval (2 ; +∞).
That is, the solution of the original inequality is the set of x < -2 and x > 2
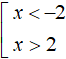
We will call a set of inequalities united by a square bracket and which have many solutions satisfying at least one of the inequalities in the set.
To write the final answer, the intervals x < -2 and x > 2 must be combined. In mathematics, the union sign is ∪. Then:
x ∈ (−∞ ; −2) ∪ (2 ; +∞)
The union sign ∪ reads "or". Then the notation x ∈ (-∞ ; -2) ∪ (2 ; +∞) can be read as follows:
The value of the variable x belongs to the interval (-∞ ; -2) or to the interval (2 ; +∞)
Indeed, if we substitute any value of x which is a solution of the original inequality, then this value will belong to the interval (-∞ ; -2) or the interval (2 ; +∞).
For example, the number 3, is a solution of the original inequality |x| > 2
|3| > 2 ⇔ 3 > 2
The value of 3 belongs to the interval (2 ; +∞). It also satisfies at least one of the inequalities of the set 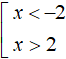 , namely the inequality x>2.
, namely the inequality x>2.
The value -4 is also a solution of the original inequality |x| > 2. This value belongs to the interval (-∞ ; -2)
|−4| > 2 ⇔ 4 > 2
Also the value -4 satisfies at least one of the inequalities of set 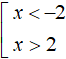 , namely the inequality x < -2.
, namely the inequality x < -2.
According to the definition, the modulus of number x is the distance from the origin to the point x. In the inequality |x| > 2 this distance is greater than 2.
Indeed, from the origin (point 0) any distance greater than two will be a solution to the inequality |x| > 2

Answer: x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Note that the boundaries -2 and 2 are not included in the corresponding intervals. This is because when you substitute these numbers into the original inequality, you get the wrong inequality.
Now let's change our example a bit. In the inequality|x| > 2, change the sign > to a sign <
|x| < 2
Let us solve this inequality.
As before, we first solve the modulus. If the submodular expression is greater than or equal to zero, we get the inequality x < 2. The solutions of this inequality are all numbers less than two. Let us note them:

And if the submodular expression is less than zero, we obtain the inequality -x < 2. Multiply both parts of this inequality by -1. Then we obtain the inequality x > -2. The solutions of this inequality are all numbers greater than -2. Mark these solutions in the same figure where we marked solutions to the inequality x < 2.
For clarity, the solutions to the inequality x > -2 are marked in red:

If the expression |x| is the distance from the origin to the point x, then the inequality |x| < 2 says that this distance is less than 2. You can see in the figure that from the origin the distances less than 2 lie between -2 to 0 and 0 to 2.

And these distances will simultaneously belong to the intervals x < 2 and x > -2
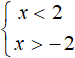
Note that this time the intervals are framed by the system sign, not the population sign as in the last example. This means that the values of x simultaneously satisfy both inequalities (intervals x < 2 and x > -2)
That is, the solution of the inequality |x| < 2 is the intersection of the intervals x < 2 and x > -2. Recall that the intersection of two intervals is an interval consisting of numbers that belong to both the first interval and the second:
x ∈ (−2 ; 0) ∩ (0 ; 2)
The intersection sign ∩ reads as "and". Then the notation x ∈ (-∞ ; 2) ∩ (-2 ; +∞) can be read as follows:
The value of the variable x simultaneously belongs to the interval (-∞ ; 2) and the interval (-2 ; +∞)
Indeed, if we substitute any value of x which is a solution of the inequality |x| < 2, then this value will belong to both (-∞ ; 2) and (-2 ; +∞) intervals.
For example, number 1 is a solution of the original inequality |x| < 2
|1| < 2 ⇔ 1 < 2
The value 1 simultaneously belongs to the interval (-∞ ; 2) and the interval (-2 ; +∞)

Also, the value of 1 satisfies both inequalities of the system 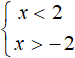
And if you substitute a value that is not a solution of the inequality |x| < 2, then this value will not simultaneously belong to the intervals (-∞ ; 2) and (-2 ; +∞). For example, the value of 7
|7| < 2 ⇔ 7 < 2
In spite of the fact that value 7 belongs to one of the intervals, namely the interval (-2 ; +∞), this value is not a solution of the original inequality, because it does not satisfy it. Also, this value does not belong to both intervals: (-∞ ; 2) and (-2 ; +∞).
For the inequality |x| < 2 the answer can be written in shorter form:
x ∈ (−2 ; 2)
From these examples we can see that the solution of an inequality with a module can be either the union of intervals or their intersection.
In the first example we solved an inequality |x| > 2, that is, an inequality of the form |x| > a. This is an inequality in which the modulus is greater than some number or letter expression. The solution to such an inequality is the union of the solutions to the inequalities obtained after exposing the modulus of the original inequality. Inequalities obtained after exposing the modulus should be written as an aggregate:
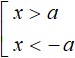
A set is reduced because the final solutions will satisfy at least one of the inequalities obtained after exposing the modulus of the original inequality.
In the second example we solved the inequality |x| < 2, i.e. an inequality of the form |x| < a. It differs from the previous inequality only by the sign. But it is an inequality where the modulus is less than some number or alphabetic expression. The solution of such an inequality is the intersection of the solutions of the inequalities obtained after exposing the modulus of the original inequality. Inequalities obtained after exposing the modulus should be written as a system:
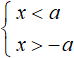
The system is written because the final solutions will satisfy both inequalities obtained after exposing the modulus of the original inequality.
The same rules hold for inequalities containing signs ≥ and ≤
For example, solve the inequality |x| ≥ 1. The module is greater than or equal to a number. Therefore the solution will be the union of solutions of the inequalities that will be obtained after exposing the modulus. After exposing the modulus and performing the necessary identity transformations, we obtain the set of inequalities x ≥ 1 and x ≤ -1
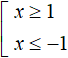

The solution is the union of the intervals x ≤ -1 and x ≥ 1
x ∈ (−∞ ; −1] ∪ [1 ; +∞)
Note that the boundaries -1 and 1 are included in the corresponding intervals. This is because when you substitute these numbers into the original inequality, you get the correct inequality.
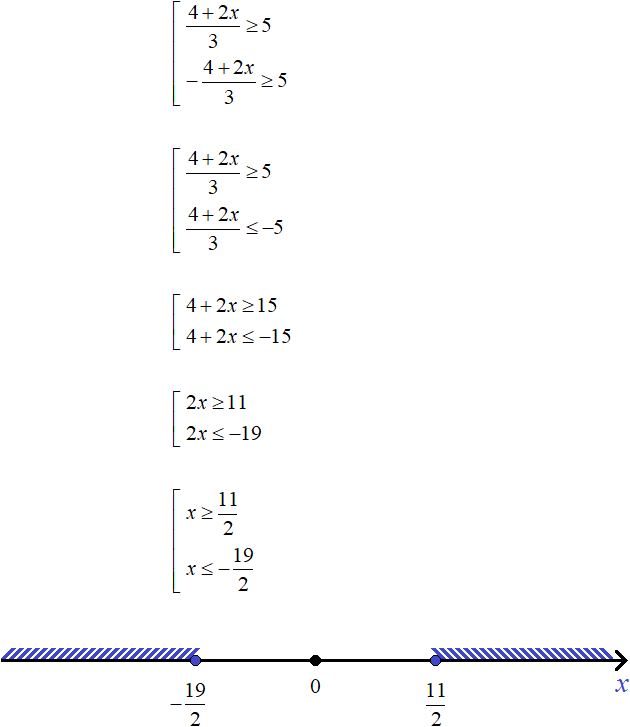
Now solve for example the inequality |x| ≤ 1. The module is less than or equal to a number. Therefore the solution will be the intersection of the solutions of the inequalities, which will be obtained after exposing the modulus. After exposing the modulus and performing the necessary identity transformations, we obtain a system of inequalities: x ≤ 1 and x ≥ -1
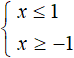

The solution is the intersection of the intervals x ≤ 1 and x ≥ -1
x ∈ (−∞ ; 1] ∩ [−1 ; +∞)
or shorter:
x ∈ [−1 ; 1]
Note that the boundaries -1 and 1 are included in the corresponding intervals. This is because when you substitute these numbers into the original inequality, you get the correct inequality.
Similarly, you can solve inequalities with a module on the left side and a letter expression on the right side.
Example 4. Solve the inequality |7x - 6| < x + 12
Solution
First, let's expand the modulus. Recall that if an inequality contains the sign < or ≤, then the inequalities obtained after exposing the module should be written as a system. This means that the final solutions will satisfy both inequalities.
So, after expanding the module we get the following system:
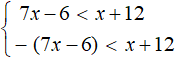
In this case the system contains not quite elementary inequalities as in the previous examples. These inequalities should be simplified using known identity transformations.
Open the brackets in the second inequality. Then we obtain the following system:
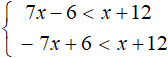
In both inequalities, move the expressions containing the unknowns to the left side and the numeric expressions to the right. Then we add like terms. Then we obtain a system:
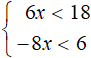
In the first inequality, divide both parts by 6. In the second inequality, divide both parts by -8. Then we obtain the final system:
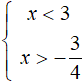
Let's represent the solutions on the coordinate line:

The solution is the intersection of intervals (-∞ ; 3) and 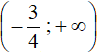 , that is, interval
, that is, interval 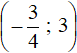
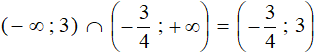
Answer: 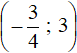
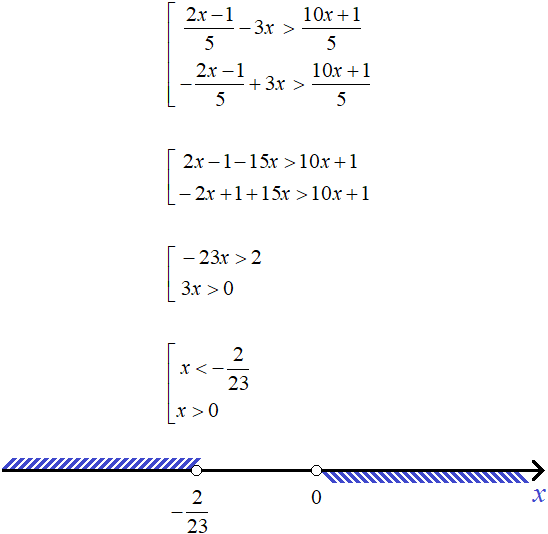
Example 5. Solve the inequality |1 - 2x| ≥ 4 - 5x
Solution
First, let's expand the modulus. Recall that if an inequality contains the sign > or ≥, then the inequalities obtained after expanding the module should be written as a set:
After expanding the modulus, we obtain the following set:
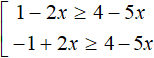
Perform the necessary identity transformations in both inequalities. As a result, we obtain:
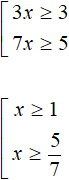
Let's represent the solutions on the coordinate line:

The solution is the union of intervals 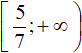 and [1 ; +∞), that is, interval
and [1 ; +∞), that is, interval 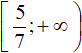
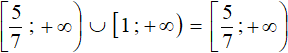
Answer: 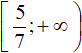 .
.
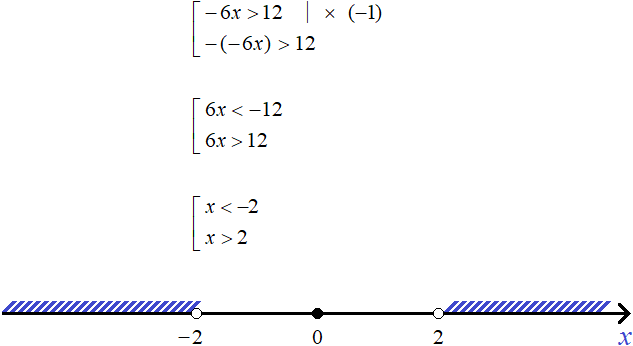
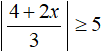
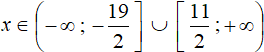
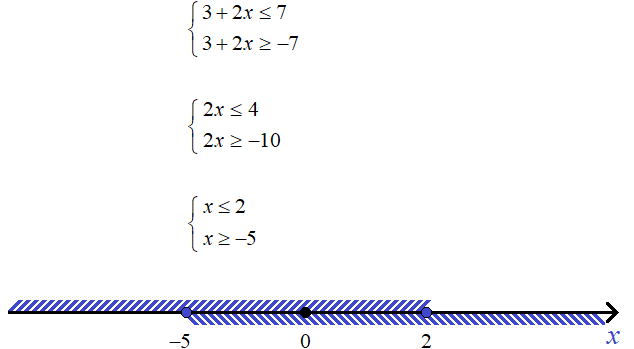
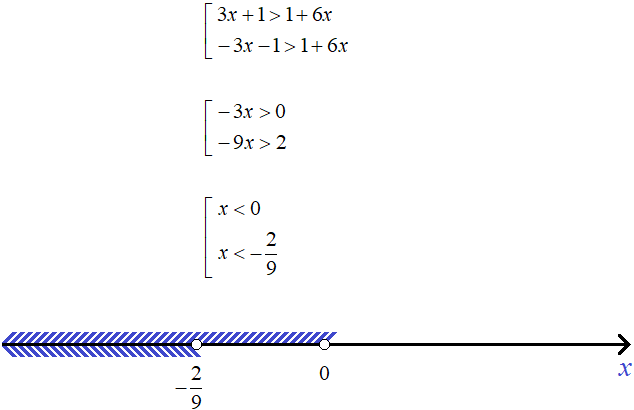
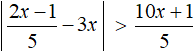
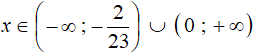
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.