What is a set?

A set is a collection of distinct elements or members. The members that make up a set are called elements of the set.

For example: a set of schoolchildren, a set of cars, a set of numbers.

In mathematics, the set is treated much more broadly. We will not delve too deeply into this topic, since it belongs to higher mathematics and can be difficult to learn at first. We will consider only the part of the topic that we have already dealt with.

Designations

The set is usually denoted by capital letters of the Latin alphabet, and its elements by lowercase letters. At that, elements are enclosed in curly parentheses.

For example, if our friends names are Tom, John and Leo, then we can define a set of friends, the elements of which are Tom, John and Leo.

Denote the set of our friends by the capital Latin letter F (friends), then put an equal sign and list our friends in curly parentheses:

F = { Tom, John, Leo }

Example 2. Write a set of divisors of number 6.

Denote this set by any capital Latin letter, for example, by the letter D

D

then put an equal sign and in curly parentheses list the elements of the set, that is, list the divisors of number 6

D = { 1, 2, 3, 6 }

If an element belongs to a given set, it is indicated by an accessory sign - ∈. For example, the divisor 2 belongs to the set of divisors of number 6 (set D). The way it is written is as follows:

2 ∈ D

Reads as "2 belongs to the set of divisors of number 6".

If an element does not belong to a given set, it is indicated by a strikethrough sign - ∉. For example, the divisor 5 does not belong to D. It is written as follows:

5 ∉ D

Reads "5 does not belong to the set of divisors of 6".

In addition, a set can be written as a direct enumeration of elements, without capital letters. This can be convenient if the set consists of a small number of elements.

For example, set a set with one element. Let this element be our friend Tom:

{ Tom }

Let's set a set that consists of one number 2

{ 2 }

Let's set a set that consists of two numbers: 2 and 5

{ 2, 5 }

Set of natural numbers

This is the first set we started working with. Natural numbers are numbers 1, 2, 3, etc.

Natural numbers appeared because of the need of people to count certain objects.

For example, to count the number of chickens, cows, horses. Natural numbers arise naturally when counting.

In past lessons, when we used the word "number", we most often meant a natural number.

In mathematics, a set of natural numbers is denoted by the capital Latin letter N.

For example, let us specify that the number 1 belongs to the set of natural numbers. To do this, we write down the number 1, then use the membership symbol ∈ to say that the one belongs to the set N

1 ∈ N

It reads as: "the unit belongs to the set of natural numbers".

Set of integers

The set of integers includes all positive and negative numbers, as well as the number 0.

The set of integers is denoted by the capital Latin letter Z.

Let us say, for example, that the number -5 belongs to the set of integers:

−5 ∈ Z

Let's specify that 10 belongs to the set of integers:

10 ∈ Z

Let's specify that 0 belongs to the set of integers:

0 ∈ Z

In the future, we will call all positive and negative numbers with one phrase - integers.

Set of rational numbers

Rational numbers, these are the same common fractions we study to this day.

A rational number is a number that can be represented as a fraction , where a is the numerator of the fraction, b is the denominator.

The numerator and denominator can be any numbers, including integers (except for zero, because you cannot divide by zero).

For example, suppose a is replaced by 10 and b is replaced by 2

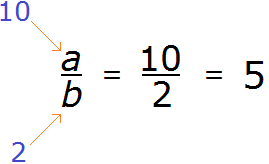
10 divided by 2 equals 5. We see that number 5 can be represented as a fraction , which means that number 5 is part of the set of rational numbers.

It is easy to see that number 5 also belongs to the set of integers. Therefore, the set of integers is part of the set of rational numbers. This means that the set of rational numbers includes not only fractions, but also integers like -2, -1, 0, 1, 2.

Now imagine that instead of a there is number 12 and instead of b there is number 5.

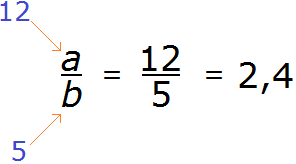
12 divided by 5 equals 2.4. We see that the decimal 2.4 can be represented as a fraction , so it is part of the set of rational numbers. Hence we conclude that the set of rational numbers includes not only fractions and integers, but also decimal fractions.

We calculated the fraction and got the answer 2.4. But we could have isolated an integer part in this fraction:

If we extract the integer part in the fraction , we get the mixed number . We see that the mixed number can also be represented as a fraction .

So the set of rational numbers includes mixed numbers.

As a result, we conclude that the set of rational numbers contains:

• integers
• fractions
• decimals
• mixed numbers

The set of rational numbers is denoted by the capital Latin letter Q.

For example, we say that belongs to the set of rational numbers. To do this, we write the fraction itself, then use an accessory sign ∈ to say that the fraction belongs to the set of rational numbers:

∈ Q

Note that the decimal 4.5 belongs to the set of rational numbers:

4,5 ∈ Q

Let's specify that the mixed number belongs to the set of rational numbers:

 ∈ Q

This introductory lesson on sets is now complete. In the future we will take a much better look at sets, but for now this lesson is over.

Video lesson

Add comment