Power function

A function of type is called a quadratic function, and its graph is called a parabola. If , then the branches of the parabola "look up", if , then down.

You know the simplest parabola very well: (see below). Note that the graph of this function is symmetric about the -axis. Such functions are called even functions. Parity is expressed analytically by the condition . Let us check for evenness of our function by substituting instead of :

, so the function is even.

In the general case the quadratic function is not even, but nobody cancelled the symmetry of the parabola itself and it is convenient to use in practice.

How to quickly construct any parabola? Obviously, it is advantageous to find its vertex first, and then to find several pairs of symmetric points. Let's see how this happens using the example of the function :
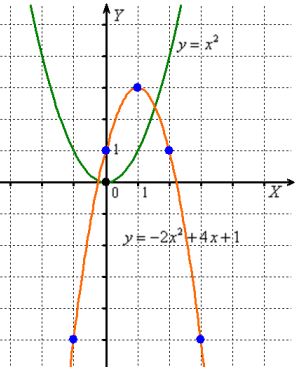First, we find the vertex by taking the derivative and equating it to zero:  
Let's find the root of the equation: - here is the vertex, its "Y": 

Now find the reference points (usually four are enough), using the symmetry of the parabola and the "left-right" principle:

Attention! To check, calculate both values, they must coincide!

The steps listed are usually done verbally or on a draft, and the results are entered into a spreadsheet:

It remains to mark the found points on the drawing and CURRENTly connect them with a line. The considered algorithm is not necessary and in simple cases a vertex of a parabola can be found simply by going through the points.

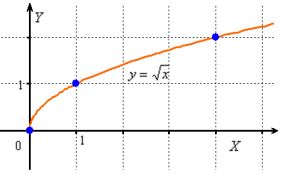The graph of the function is a branch of a parabola that "lies on its side":
As already noted, this function is defined only for non-negative "X": ,
and it is convenient to use the following anchor points to construct the graph:

The graph of function is called a cubic parabola. This function is symmetric about the beginning of coordinates, and such functions are called odd functions.

Analytically, the oddness is expressed by the condition . Let's check our function for oddness by substituting instead of :  ,

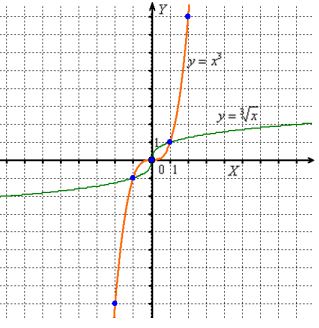
To build a cubic parabola it is enough to mark points:

then take advantage of symmetry or just the oddness of the function:
.
The graph of function is a cubic parabola "lying on its side". In contrast to , this function is defined for all "X": and is also odd, because the "minus" is safely carried forward:

The graph of an arbitrary root with a fractional exponent should be plotted, bearing in mind the area of determination of one or another root.

So, the function , like , is defined only for non-negative "X": and to construct its graph you will have to find several values approximately:

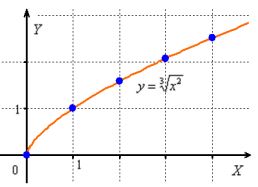
Such values are called "bad" in mathematical jargon, but what can you do....
This function is not even or odd, because it is not defined for negative "X", which means that the condition or simply cannot be met.

The graph of the function is a hyperbola. Yes, it is also a power function! For . If , then the branches of the hyperbola lie in the 1st and 3rd coordinate quarters, if , then in the 2nd and 4th coordinate quarters (see examples in the drawing below).

Obviously, we are facing an odd function, because: .
This function is not defined at point , and the coordinate axes are asymptotes of the graph - you cannot "climb on them"!  An asymptote is a line to which the graph approaches infinitely close, but does not cross it.

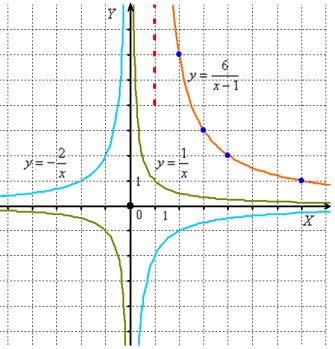
How do I quickly graph a hyperbola? (and not just any hyperbola)
In many cases it is convenient to draw a point-by-point, let's build, for example, the right branch of .
This function is not defined at point , so the vertical asymptote will be exactly here.
Let's find several reference points (selecting convenient values of "X"):

Mark these points on the drawing and carefully connect them with a line.

Essentially the same form has graphs - only in the first case the hyperbola will have one branch, in the second - two branches located in the 1st and 2nd coordinate quarters, and the third hyperbola will be similar to .

Exercises

Task 1. Solve graphically he system of equations
.

Solution:

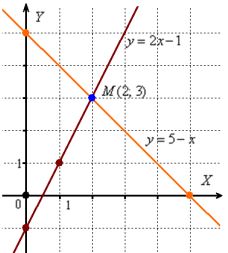Here you need to draw two lines and determine their point of intersection. Its coordinates will be the solution of the system.
From the first equation we express:
x + y = 5 => y = 5- x, let's select the following reference points:

To plot -2x + y = -1 => y = 2x - 1 it is convenient to choose the points:

It follows from the drawing that the lines intersect at the point M(2; 3)
Answer:
x = 2, y = 3

Show Solution

Task 2. Draw a graph . Recall how to expand the module.

Solution:

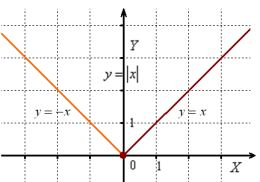Expanding the module:
Such functions are called piecewise functions.
Plotting the graphs of the functions y = -x, y = x on the corresponding intervals.
The function "module x" is even, since:
, its graph is symmetric about the axis OY.

Show Solution

Task 3. Check functions for even / oddness and plot their graphs:
.

Solution:

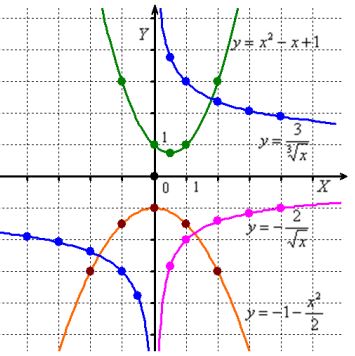1.) Check for an even/odd function

it means that this function is not even or odd.
When finding the anchor points, we we get symmetric ones at once, from which it is clear where the vertex is:

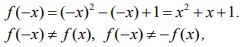
2.) Let's check the function

means that it is even and there are no problems with the vertex and reference points there is no problem.
3.) The function is defined only for x > 0 and therefore cannot be even or odd. Find some reference points and draw a branch of the hyperbola:

4.) Let's investigate the function , it means, this function is odd and its graph is symmetric with respect to the origin coordinates. To construct a hyperbola, it is sufficient to find several points of the right branch:

We find the points of the left branch from symmetry considerations or by using the analytical condition of oddness, for example: ƒ(-1) = -3 .

Show Solution

Task 4. Given - equation of the circle with center at the origin of radius . Express the functions defining the upper and lower half-circle, indicate their fields of definition.

Solution:

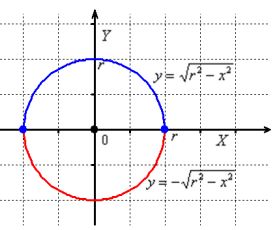Write the equation as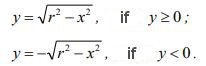 and take the square root of both parts: . On the left side we should put the modulus: and expand it:

The first function defines the upper half-circle (since "Y" are non-negative), and the second function the lower half-circle.
The domain of each function is Obviously, both functions are even and their graphs are symmetric about the OY axis.

Show Solution

Add comment