What is called a theorem?
If a person has discovered a pattern in mathematics that allows him to solve a problem quickly, he should not say that he has made a discovery. Because it may happen that this pattern works only for certain cases, and for others it does not work or solves the problem incorrectly at all.
To share your discovery with others, formulate the pattern found as a statement, and then prove the statement with undeniable facts.
The formulated statement is called a theorem. And the proof of a theorem consists of facts, logical reasoning, and calculations that are not challenged.
For example, the following statement can be called a theorem:
«If the numerator and denominator of an ordinary fraction are multiplied by some number, the value of the fraction will not change».
And then give such proof:
Suppose there is a fraction 
. Multiply the numerator and denominator of this fraction by the number c. Then we have the fraction 
. Prove that fractions and are equal. That is, prove that the equality 
is true.
To prove this equality, we will use the basic property of the proportion:
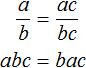
The product does not change due to the rearrangement of the places of the factors. Therefore in the resulting equality the right part can be ordered alphabetically:
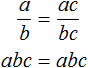
Since equality is a proportion, and a proportion is an equality of two relations, fractions and 
are equal. The theorem is proved.
Viette's Theorem
The French mathematician François Viett discovered an interesting relationship between the coefficients of a given quadratic equation and the roots of the same equation. This relationship is represented in the form of a theorem and is formulated as follows:
The sum of the roots of the quadratic equation x2 + bx + c = 0 equals the second quotient taken with the opposite sign, and the product of the roots equals the free term.
That is, if you have the above quadratic equation x2 + bx + c = 0, and its roots are the numbers x1 and x2, then the following two equations are true:
The system sign (curly bracket) indicates that the values of x1 and x2 satisfy both equalities.
Let's show the Viets theorem by the example of the given quadratic equation x2 + 4x + 3 = 0.
We do not yet know which roots of the equation x2 + 4x + 3 = 0. But by Viet's theorem we can write that the sum of these roots is equal to the second coefficient 4 taken with the opposite sign. If the coefficient of 4 is taken with an opposite sign we obtain -4. Then:
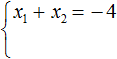
And the product of the roots according to the Viets theorem will be equal to the free term. In the equation x2 + 4x + 3 = 0, the free term is 3. Then:
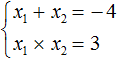
Now check if the sum of the roots is really -4, and if the product is equal to 3. To do this, find the roots of the equation x2 + 4x + 3 = 0. And for convenience we use the formulas for the even second coefficient:
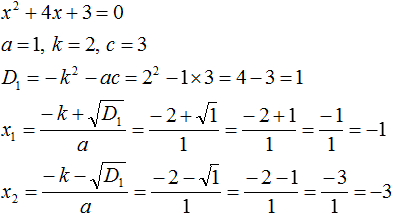
The roots of the equation are the numbers -1 and -3. According to Viet's theorem, their sum should be equal to the second coefficient of the equation x2 + 4x + 3 = 0, taken with the opposite sign. Indeed, this is the case. The second coefficient in the equation x2 + 4x + 3 = 0 is 4. If you take it with the opposite sign and equate the sum of the roots x1 + x2 to this coefficient, you get the correct equality:
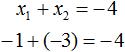
And the product of the roots -1 and -3 according to the Viet theorem should be equal to the free term of the equation x2 + 4x + 3 = 0, i.e. number 3. We see that this condition is also satisfied:
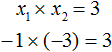
So expression 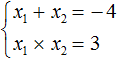is valid.
Consider the quadratic equation x2 - 8x + 15 = 0. According to Viet's theorem, the sum of the roots of this equation is equal to the second coefficient taken with the opposite sign. The second coefficient is -8. If we take it with the opposite sign, we get 8. Then:
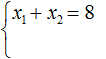
And the product of the roots is equal to the free term. In the equation x2 - 8x + 15 = 0, the free term is 15. Then:
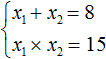
Now check if the sum of the roots is really 8, and if the product is 15. To do this, find the roots of this equation. And for convenience, we use the formulas for the even second coefficient. This time we will skip some detailed notes:
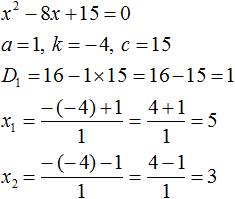
We see that the roots of the equation x2 - 8x + 15 = 0 are numbers 5 and 3. Their sum is 8. That is, the sum of the roots is equal to the second coefficient of the equation x2 - 8x + 15 = 0, taken with the opposite sign.
And the product of the numbers 5 and 3 is 15. That is, it is equal to the free term of the equation x2 - 8x + 15 = 0.
So expression 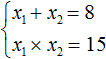is valid.
Note. In order for Viette's theorem to hold, a quadratic equation must be reduced and have roots.
For example, consider the quadratic equation x2 - 2x + 4 = 0. Write the sum and product of the roots of this equation:
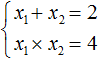
But the equation x2 - 2x + 4 = 0 has no roots whose sum is 2 and whose product is 4. You can verify this by calculating the discriminant:
D1 = k2 − ac = (−1)2 − 1 × 4 = −3
So it makes no sense to write the expression .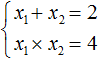
Viette's theorem is useful in that it allows you to know the signs of the roots of the equation before you start solving it.
For example, write down for the equation x2 - 5x + 6 = 0 the sum and product of its roots. The sum of the roots equals the second coefficient taken with the opposite sign, and the product of the roots equals the free term:
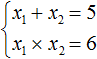
Looking at these two equations you can immediately understand that both roots must be positive. Because the product x1 × x2 = 6 will only hold in two cases: if the values of x1 and x2 are positive or they are both negative. If these values are negative, then the equality x1 + x2 = 5 will not hold, because its right-hand side is a positive number. And the values of x1 and x2 must satisfy both x1 + x2 = 5 and x1 × x2 = 6.
Another use of Vyet's theorem is that the roots can be found by fitting. In this example, the roots must be such that they satisfy both x1 + x2 = 5 and x1 × x2 = 6. Obviously, these are roots 3 and 2.
So, x1 = 3, x2 = 2
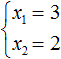
Proof of the Viette Theorem
Let the above quadratic equation x2 + bx + c = 0 be given. If its discriminant is greater than zero, then it has two roots, the sum of which is equal to the second coefficient taken with opposite sign, and the product of the roots is equal to the free term:
Let us prove that the equations x1 + x2 = −b and x1 × x2 = c exist.
Recall the formulas for the roots of a quadratic equation:
Find the sum of the roots x1 and x2. To do this, substitute in the expression x1 + x2 instead of x1 and x2 the corresponding expressions from the right side of the formulas for the roots of the quadratic equation. Keep in mind that in the above quadratic equation x2 + bx + c = 0, the major factor a is one. Then in the process of substitution the denominator becomes equal to just 2
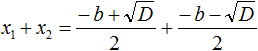
Write the right part as a fraction with one denominator:
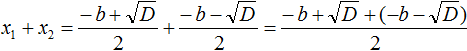
Open the brackets in the numerator and give like terms:
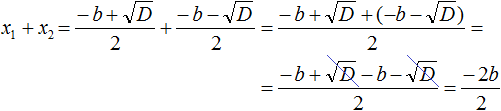
Let's reduce the fraction 
by 2, then we get −b
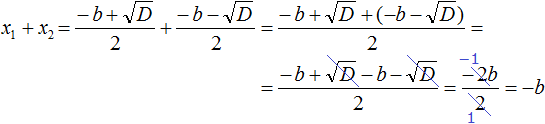
So x1 + x2 really equals −b
x1 + x2 = −b
Now similarly prove that the product x1 × x2 is equal to the free term c.
Instead of x1 and x2 we substitute the corresponding expressions from the formulas for the roots of the quadratic equation. Do not forget that the coefficient a is still equal to one:
To multiply fractions, multiply their numerators and denominators:
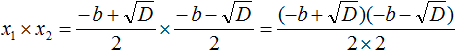
The numerator now contains the product of the sum of two expressions and the difference of the same expressions. Use the identity (a + b)(a − b) = a2 − b2.
Then the numerator will be 
and the denominator will be 4
Now the numerator expression (-b)2 will become b2, and the expression 
will become just D
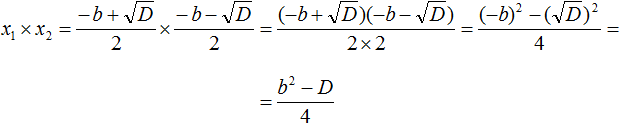
But D is equal to b2 − 4ac. Let's substitute this expression for D, remembering that a = 1. That is, instead of b2 − 4ac we substitute b2 − 4c
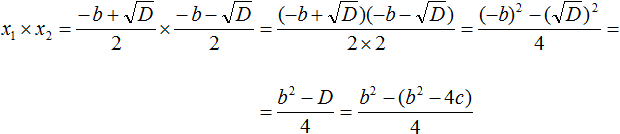
In the resulting expression, open the brackets in the numerator and give like terms:
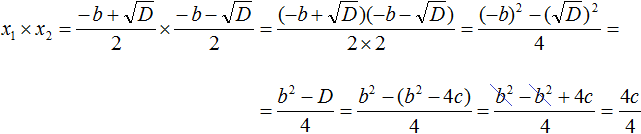
Let's reduce the resulting fraction by 4
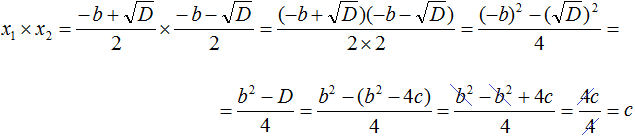
So x1 × x2 really is c.
x1 × x2 = c
Thus, the sum of the roots of the quadratic equation given x2 + bx + c = 0 equals the second coefficient taken with the opposite sign (x1 + x2 = −b), and the product of the roots equals the free term (x1 × x2 = c). The theorem is proved.
Theorem, the inverse of the Viette theorem
When the sum and product of the roots of a given quadratic equation are written down, one usually begins to find suitable roots to that equation. At this point, the so-called inverse theorem of the Viets theorem comes into play. It is formulated as follows:
If the numbers x1 and x2 are such that their sum is equal to the second coefficient of the equation x2 + bx + c = 0, taken with the opposite sign, and the product of the numbers x1 and x2 is equal to the free term of the equation x2 + bx + c = 0, then the numbers x1 and x2 are roots of the equation x2 + bx + c = 0.
Inverse theorems can be stated in such a way that their statement is the conclusion of the first theorem.
Thus, by proving Viette's theorem we conclude that the sum of x1 and x2 equals -b, and the product of x1 and x2 equals c. In the inverse theorem this conclusion serves as an assertion.
Earlier we solved the equation x2 - 5x + 6 = 0 and wrote for it this sum and product of the roots:
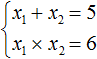
And then we picked up roots 3 and 2. In fact, we have applied a theorem that is the inverse of Viet's theorem. The numbers 3 and 2 are such that their sum is equal to the second coefficient of the equation x2 - 5x + 6 = 0 taken with the opposite sign (number 5), and the product of numbers 3 and 2 is equal to the free term (number 6). So the numbers 3 and 2 are roots of the equation x2 - 5x + 6 = 0.
Example 2. Solve the quadratic equation x2 - 6x + 8 = 0 by the inverse theorem of Viet's theorem.
In this equation a = 1. So the quadratic equation is a reduced equation. It can be solved by the inverse theorem of Viet's theorem.
First write down the sum and product of the roots of the equation. The sum of the roots will be 6 because the second coefficient of the original equation is -6. And the product of the roots is 8
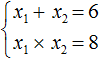
Now having these two equations you can find the appropriate roots. They must satisfy both x1 + x2 = 6 and x1 × x2 = 8.
It is more convenient to find the roots by their product. Using the equality x1 × x2 = 8, find x1 and x2 whose product is 8.
The number 8 can be obtained by multiplying the numbers 4 and 2 or 1 and 8.
4 × 2 = 8
1 × 8 = 8
But the values of x1 and x2 must be chosen so that they satisfy not only the equality x1 × x2 = 8, but also the equality x1 + x2 = 6.
Immediately we conclude that the values 1 and 8 are not suitable, because although they satisfy the equality x1 × x2 = 8, they do not satisfy the equality x1 + x2 = 6.
But the values 4 and 2 fit both x1 × x2 = 8 and x1 + x2 = 6, because these values satisfy both equations:
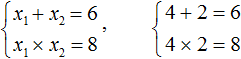
So the roots of the equation x2 − 6x + 8 = 0 are the numbers 4 and 2.
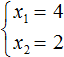
The inverse theorem, like any theorem, needs a proof. Let us prove the inverse theorem of Viet's theorem. For convenience we denote the roots x1 and x2 as m and n. Then the statement of the inverse theorem will take the following form:
If the numbers m and n are such that their sum is equal to the second coefficient of the equation x2 + bx + c = 0, taken with the opposite sign, and the product of the numbers m and n is equal to the free term of the equation x2 + bx + c = 0, then the numbers m and n are roots of the equation x2 + bx + c = 0
First, write that the sum of m and n is -b, and the product of mn is c
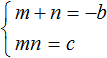
To prove that the numbers m and n are roots of the equation x2 + bx + c = 0, you need to alternately put the letters m and n in this equation instead of x, then perform possible identity transformations. If the transformations result in the left-hand side being equal to zero, it means that the numbers m and n are the roots of the equation x2 + bx + c = 0.
In addition to the letters m and n, we need to know what the parameter b is. Express it from the equality m + n = -b. The easiest way to do this is to multiply both parts of this equation by -1
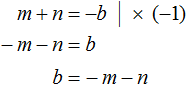
Now everything is ready for substitution. Substitute m into the equation x2 + bx + c = 0 instead of x, and substitute the expression -m - n instead of b
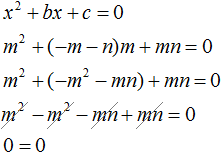
We see that x = m results in the correct equality. So the number m is the root of the equation x2 + bx + c = 0.
Similarly, prove that the number n is the root of the equation x2 + bx + c = 0. Instead of x we substitute the letter n, and instead of c we substitute mn, since c = mn.
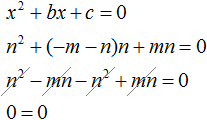
We see that x = n also results in the correct equality. So the number n is the root of the equation.
Consequently, the numbers m and n are roots of the equation x2 + bx + c = 0.
Examples of solving equations by the inverse of the Viette theorem
Example 1. Solve the quadratic equation x2 - 4x + 4 = 0 by the inverse theorem of Viet's theorem.
Write down the sum of the roots x1 and x2 and equate it with the second coefficient taken with the opposite sign. Also write down the product of the roots x1 and x2 and equate it to the free term:
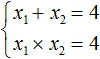
In this example, it is obvious that the roots are 2 and 2. Because their sum is 4 and their product is 4
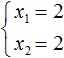
The value of x1 is the same as x2. This is the case when a quadratic equation has only one root. If we try to solve this equation using the formulas for the roots of the quadratic equation, we find that the discriminant is zero and the root is calculated using the formula 
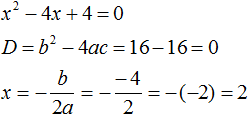
This example shows that the inverse theorem works for equations with only one root. A sign that a quadratic equation has only one root is that the values of x1 and x2 coincide.
Example 2. Solve the quadratic equation x2 + 3x + 2 = 0 by the inverse theorem of Viet's theorem.
Write down the sum and product of the roots of this equation:
Now let's pick up the values of x1 and x2. Here begins the most interesting part. The product of the roots is 2. The number 2 can be obtained by multiplying 1 and 2. But the sum of the roots x1 + x2 is a negative number -3. So the values of 1 and 2 do not fit.
A sum is negative if both summands are negative, or one summand whose modulus is greater is negative.
If we choose roots with different signs, the equality x1 × x2 = 2 will not be fulfilled.
If we choose positive roots, the equality x1 × x2 = 2 will be fulfilled, but the equality x1 + x2 = −3 will not be fulfilled.
Obviously, the roots are two negative numbers. The product of negative numbers is a positive number. And the sum of negative numbers is a negative number.
Then the equations will satisfy the numbers -1 and -2.
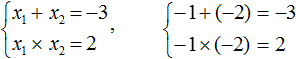
So, the roots are the numbers -1 and -2
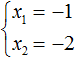
Example 3. Solve the equation x2 + 16x + 15 = 0 by the inverse of Viet's theorem.
Write down the sum and product of the roots of this equation:
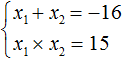
As in the last example, the sum of the roots is a negative number and the product of the roots is a positive number.
The product is positive if both factors are positive or both factors are negative. The first option is rejected immediately because the sum of the roots equals a negative number. Then both roots are negative. Let us try to find them.
The number 15 can be obtained by multiplying the numbers -1 and -15 or (-3) and (-5). In this case, the first option is suitable because the sum of numbers -1 and -15 is -16, and their product is 15. Thus the roots of the equation x2 + 16x + 15 = 0 are -1 and -15
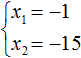
Example 4. Solve the equation x2 − 10x − 39 = 0 by the inverse of Viet's theorem.
Write down the sum and product of the roots of this equation:
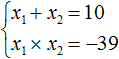
The product of the roots is a negative number. So one of the roots is negative. The number -39 can be obtained by multiplying the numbers -3 and 13 or -13 and 3. Of these combinations, the combination of -3 and 13 is more suitable, since multiplying these numbers results in -39, and adding 10
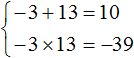
So the roots of the equation x2 - 10x - 39 = 0 are -3 and 13.
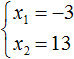
Example 5. The first root of the equation x2 + bx + 45 = 0 is 15. Find the second root of the equation and the value of the coefficient b.
According to Viet's theorem, the product of the roots of a given quadratic equation is equal to the free term. In this case this product is 45
x1 × x2 = 45
In this case, one of the roots is already known - it is root 15.
15 × x2 = 45
Then the second root will be 3, because number 45 is obtained if 15 is multiplied by 3.
15 × 3 = 45
So x2 = 3
This second root could also be obtained by expressing the variable x2 from the equality 15 × x2 = 45
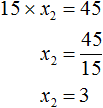
Now determine the value of the coefficient b. To do this, write the sum of the roots of the equation:
15 + 3 = 18
According to Viet's theorem, the sum of the roots of a given quadratic equation is equal to the second coefficient taken with the opposite sign. If the sum of the roots equals 18, and 18 is a positive number, then the coefficient in the equation itself will be negative:
x2 − 18x + 45 = 0
So b = −18.
Usually the solution to such a problem is written as follows. First, write down the main theorem of Viet in the form of the sum and the product of the roots:
Then we substitute the available known values into this expression. In our case we know that the first root is 15, and the free term of the equation
x2 + bx + 45 = 0 equals 45
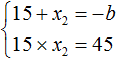
From this system we should find x2 and b. Let us express these parameters:
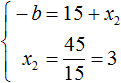
From this system we see that x2 is 3. Let's substitute it into the first equality:
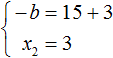
Now from the first equality we see that -b equals 18
But we are interested in b, not -b. Remember that -b is -1b. To find b, divide 18 by -1. Then b equals -18
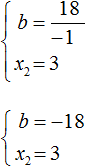
The same result can be obtained by multiplying the first equality by -1 in expression
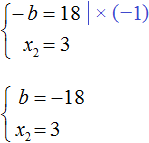
Now go back to the original equation x2 + bx + 45 = 0 and substitute the value of b
Multiply -18 by x. We obtain -18x
Open the brackets:
Example 6. Using Viet's theorem, write the given quadratic equation whose roots are the numbers 2 and 8.
In this task the roots are already known. That is, x1 = 2, x2 = 8. According to them you should make a quadratic equation of the form x2 + bx + c = 0.
Write down the sum and product of the roots:
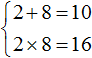
According to Viet's theorem, the sum of the roots of a given quadratic equation is equal to the second coefficient taken with opposite sign. If the sum of the roots of 2 and 8 equals 10, then the number 10 in the equation itself must have the opposite sign. So b = -10.
The product of the roots according to the Vieth theorem is equal to the free term. Our product is 16.
So b = -10, c = 16. So:
x2 − 10x + 16 = 0
Example 7. Using Viet's theorem, write the given quadratic equation whose roots are numbers 
and 
.
Write down the sum and product of the roots:
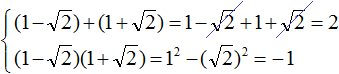
The sum of the roots is 2. Then the second coefficient in the equation is -2. And the product of the roots is -1. So the free term equals -1. Then:
x2 − 2x − 1 = 0
When the quadratic equation is not a reduced
The Vyet's theorem is valid only when the quadratic equation is a reduced equation.
If the quadratic equation is not a reduced equation, but it is still necessary to apply Viet's theorem, then both parts of the unreduced quadratic equation must be divided by the factor that comes before x2.
If, for example, in the quadratic equation ax2 + bx + c = 0 the coefficient a is not equal to one, then this equation is not reduced. To make it a reduced equation, divide both parts of it by the coefficient that is in front of x2, that is, by a
We obtain equation 
, which is a reduced equation. Its second coefficient is 
and the free term is 
. Then the sum and product of the roots will look like this:
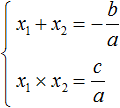
For example, solve the quadratic equation 4x2 + 5x + 1 = 0. This equation is not a reduced equation. It becomes a reduced equation if you divide both parts of it by the coefficient in front of x2, that is, by 4
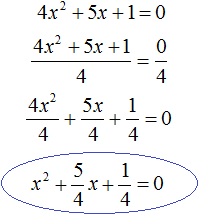
We obtained the given quadratic equation. The second coefficient is 
and the free term is 
. Then by Viet's theorem we have:
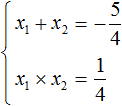
From here we find the roots -1 and 
by the fitting method
You will probably rarely use this method when solving quadratic equations. But it wouldn't hurt to know about it.
Example 2. Solve the quadratic equation 3x2 − 7x + 2 = 0
This equation is not a reduced equation, which means that it cannot yet be solved by the inverse theorem of Viet's theorem.
Let us make this equation reduced. Divide both parts by the coefficient in front of x2
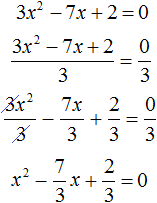
We obtained equation 
. Write down the sum and product of the roots of this equation:
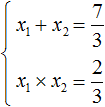
From here we find the roots of 2 and 
by fitting
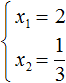
Example 3. Solve the quadratic equation 2x2 - 3x - 2 = 0
This is an unreduced quadratic equation. To make it a reduced equation, you must divide both parts of it by 2. You can do this in your head. If you divide 2x2 by 2, you get x2
Then if -3x is divided by 2, you get 
. To see where the coefficient is and where the variable is, this expression is written as 
Then if -2 divided by 2, you get -1.
Equates the resulting expression to zero:
Now we apply Viette's theorem. The sum of the roots will be equal to the second coefficient taken with the opposite sign, and the product of the roots will be the free term:
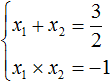
From here we find the roots of 2 and 
by fitting
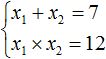
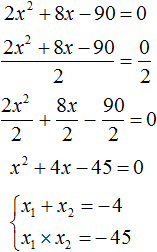
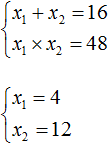
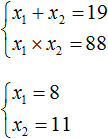
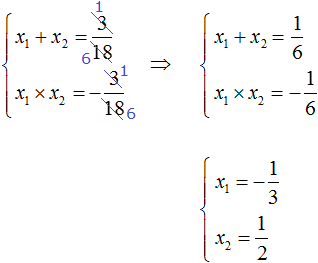
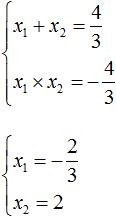
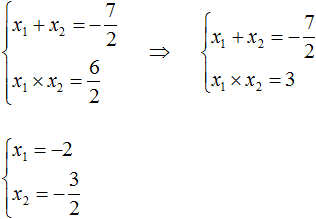
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.