The module equation is a difficult topic for beginners. With this in mind, only elementary equations will be included in this lesson.
What is an equation with a module and how do I solve it?
In equations with a modulus, the unknown value is contained under the modulus sign. For example:
|x − 2| = 5
Module equations come in different forms and are solved by different methods. You can't say that any one method is the most rational. It all depends on the original equation.
For example, in some equations you can simply guess the root, while in others you have to think logically, solve modules, and perform identity transformations. A person is free to choose which solution method to use.
For example, solve the above equation |x - 2| = 5. Suppose we don't know any method of solving it. How would we solve it?
First of all, note that the right side of this equation is equal to the number 5. On the left side is the modulus of the expression |x - 2|. This means that the submodular expression x - 2 must equal the number 5 or -5

So you need to find out at what values of the variable x the submodular expression x - 2 will turn into number 5 or -5.
The values of x can be found by equating the submodular expression to the numbers 5 and -5, and then solving each of the equations in turn:
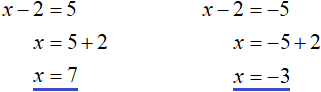
So the roots of the equation |x - 2| = 5 are the numbers 7 and -3.
Most elementary equations with modulus can be solved using the modulus expansion rule. To do this, the modulus contained in the equation is expanded, then the resulting expression is substituted in the original equation in place of the modulo expression.
We need to solve the modulus for each case: when the submodular expression is greater than or equal to zero, and when the submodular expression is less than zero.
Solve our equation |x - 2| = 5 using the modulus expansion rule. Write out its modulus separately and solve it:
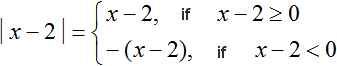
This construction says that if the submodular expression x - 2 is greater than or equal to zero, then the modulus will unfold as x - 2, and then the original equation will take the form x - 2 = 5, where x = 7
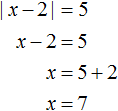
And if the submodular expression x - 2 is less than zero, then the modulus expands to -(x - 2). Then the original equation would be -(x - 2) = 5, where x = -3
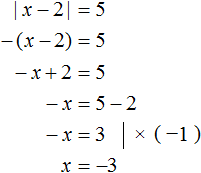
So, the equation |x - 2|= 5 has roots 7 and -3. To check, substitute the numbers 7 and -3 in the original equation instead of x. Then we obtain the correct equation:
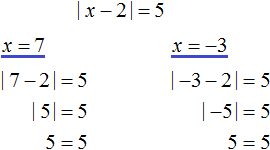
A submodular expression usually contains an x that can convert the entire submodular expression to either a positive number, a negative number, or zero.
Therefore, the modulus is revealed for each case: when the submodular expression is greater than or equal to zero, and when the submodular expression is less than zero. Each case will give an independent equation with its own root.
Let's go back now to the point where we were exposing the modulus:
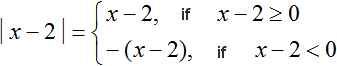
The conditions x - 2 ≥ 0 and x - 2 < 0 are inequalities that can be solved, thereby reducing them to a simple form:
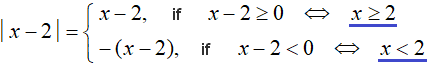
The symbol ⇔ denotes equivalence. In this case it is specified that the condition x - 2 ≥ 0 is equivalent to the condition x ≥ 2, and the condition x - 2 < 0 is equivalent to the condition x < 2.
This kind of condition recording allows you to say unambiguously at which x the module will open with a plus and at which it will open with a minus.
In the first case the condition x ≥ 2 is obtained. This means that for all x greater than or equal to 2, the module |x - 2| will expand with a plus. Thus for x = 7, the submodular expression becomes 5
|7 − 2| = |5|
Which means further disclosure will be on the plus side
|7 − 2| = |5| = 5
The module |x - 2| will behave the same way with other values of x on the interval x ≥ 2. That is, it will expand with a plus. Examples:
When x = 3, |3 − 2|=|1| = 1
When x = 4, |4 − 2|=|2| = 2
When x = 2, |2 − 2|=|0| = 0
When x = 13, |13 − 2|=|11| = 11
And in the second case the condition x < 2 is obtained. This means that for all x less than 2, the modulus will expand with a minus. For example, if x = -3, the submodular expression will again be 5. But in the intermediate calculations we can see that the modulus expands with a minus:
|−3 − 2| = |−5| = −(−5) = 5
The module |x - 2| will behave the same way with other values of x on the interval x < 2. Examples:
When x = 1, |1 − 2|=|−1| = −(−1) = 1
When x = 0, |0 − 2|=|−2| = −(−2) = 2
When x = −1, |−1 − 2|=|−3| = −(−3) = 3
When x = −9,|−9 − 2|=|−11| = −(−11) = 11
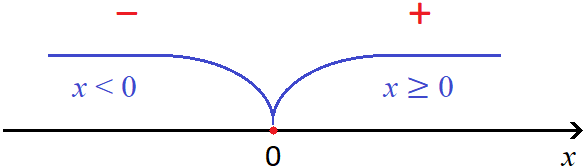
The number 2 is a kind of transition point at which the module |x - 2| changes its opening order.
You can imagine how the module |x - 2| moved along the route from minus infinity to number 2, opening at each point with minus. Once in point 2, the module changed its opening order - namely, having opened at point 2 with plus, it then began to open with plus, moving to the right side to plus infinity.
Using the coordinate line, this can be represented as follows:
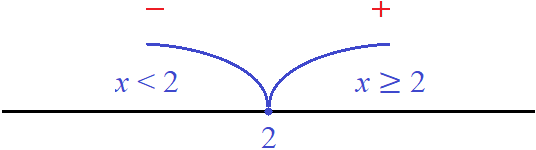
The red minus and plus signs indicate how the module |x - 2| will unfold at intervals x < 2 and x ≥ 2.
The transition point can be found for any modulus. To do this, you need to find out at which x the submodular expression is zero. Zero is the value before and after which the modulus always keeps its sign. This follows from the modulus expansion rule:
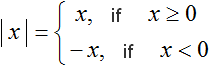
In this example, at the moment when x becomes zero, the module |x| expands with plus and then for all x greater than zero it will expand with plus. In contrast, for all x less than zero the module will open with a minus:
For example, for the module |2x + 6|, the transition point will be -3, because if you substitute 2x + 6 for x, the submodular expression will become zero. Let us illustrate this in the figure:
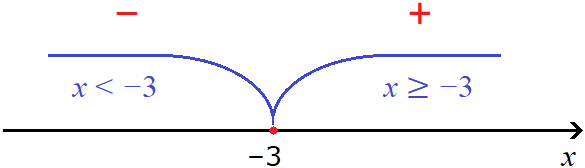
For all x greater than or equal to -3, the module will expand with a plus. Examples:
When x = -3, |2 × (-3) + 6| = |0| = 0
When x = 4, |2 × 4 + 6| = |14| = 14.
When x = 5, |2 × 5 + 6| = |16| = 16.
And for all x less than 3, the modulus will expand with a minus. Examples:
When x = -4, |2 × (-4) + 6| = |-2| = -(-2) = 2
When x = -5, |2 × (-5) + 6| = |-4| = -(-4) = 4
When x = -6, |2 × (-6) + 6| = |-6| = -(-6) = 6
Example 2. Solve the equation |x| + 3x = -2
Solution
Let's expand the modulus contained in the left part of the equation:
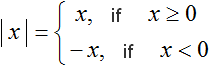
If x ≥ 0, then the modulus will expand with a plus sign and then the original equation will look like x + 3x = -2. Solve this equation immediately:
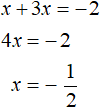
Now consider the second case - when x < 0. In this case the modulus in the original equation expands with a minus sign, and then we get the equation -x + 3x = -2. Let us solve this equation as well:
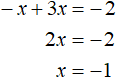
We got roots![]() and −1.
and −1.
Let's check by substituting the found roots into the original equation. Check the root ![]()
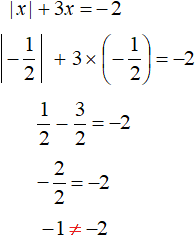
We see that by substituting the root of ![]() , the original equation does not turn into a correct equality. So
, the original equation does not turn into a correct equality. So ![]() is not the root of the original equation.
is not the root of the original equation.
Now let's check the root of -1
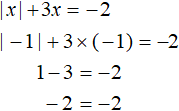
We obtained the correct equality. So of the two solutions found, only -1 is the root of the equation.
Answer: -1.
Here we can draw an important conclusion. In equations with a module, the found roots do not always satisfy the original equation. To see if your solution is correct, you need to check by substituting the found roots into the original equation.
In addition, you can check to see if the value found is a root of the equation by checking the condition according to which the modulus was expanded.
For example, in this example we expanded the module |x| for cases where the submodule expression is greater than or equal to zero, and where the submodule expression is less than zero:
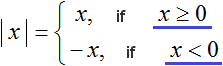
The conditions x≥0 and x<0 are inequalities. You can substitute the found roots into these inequalities. If the inequalities are true, then the roots satisfy the original equation.
So, if you expand the modulus with the plus sign, you get the equation x + 3x = -2. The root of this equation is ![]() . This number does not satisfy the condition x ≥ 0, according to which the module |x| was solved and according to which the equation x + 3x = -2 was obtained. Indeed, substituting the number
. This number does not satisfy the condition x ≥ 0, according to which the module |x| was solved and according to which the equation x + 3x = -2 was obtained. Indeed, substituting the number ![]() into the inequality x ≥ 0 results in an incorrect inequality.
into the inequality x ≥ 0 results in an incorrect inequality.
And when you expand the modulus with a minus sign, you get the equation -x + 3x = -2. The root of this equation is -1. This number satisfies the condition x<0, according to which the module |x| was solved and according to which the equation -x + 3x = -2 was obtained. Indeed, substituting the number -1 into the inequality x < 0 results in the correct inequality.
Example 3. Solve the equation |1 - 2x| - 4x = -6
Solution
Let's expand the module:
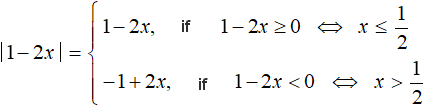
If we expand the module |1 - 2x| with the plus sign, we obtain the equation 1 - 2x - 4x = -6. Solve it:
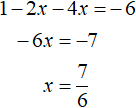
If we expand the module |1 - 2x| with a minus sign, we get the equation -1 + 2x - 4x = -6. Solve it:
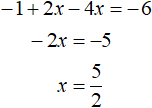
We got the roots ![]() and
and ![]() .
.
Root ![]() does not satisfy the condition
does not satisfy the condition ![]() , so it is not the root of the original equation.
, so it is not the root of the original equation.
Root ![]() satisfies the condition
satisfies the condition ![]() , so it is the root of the original equation. A check will also show this:
, so it is the root of the original equation. A check will also show this:
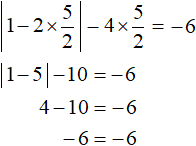
Answer: ![]() .
.
Example 4. Solve the equation |x2 − 3x| = 0
Solution
If the modulus of a number is zero, then the submodulus expression is also zero:
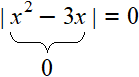
That is, you don't need to expand the modulus. It is enough to find out for which values of x the submodular expression is zero. In this case you need to solve an incomplete quadratic equation:
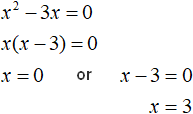
We obtained roots 0 and 3. Both roots satisfy the original equation. A check shows this:
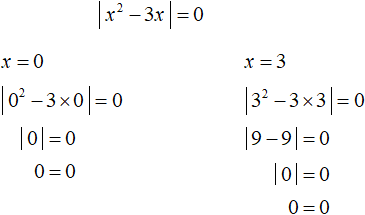
Example 5. Solve the equation x2 − 5|x| + 6 = 0
Let us write out the module |x| separately and expand it:
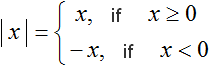
If you expand the module |x| with a plus sign, the original equation will look like x2 - 5x + 6 = 0. This is a quadratic equation. Solve it using the discriminant:
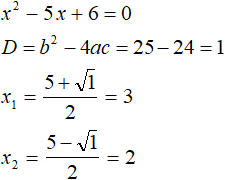
Both roots satisfy the condition x ≥ 0, so they are roots of the original equation.
If you expand the module |x| with a minus sign, the original equation will look like x2 + 5x + 6 = 0. This is also a quadratic equation. Solve it like the previous one:
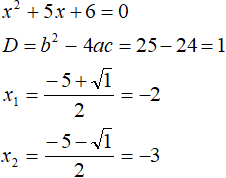
Under the condition x ≥ 0, the modulus of the equation expanded with a plus, resulting in roots 3 and 2. Both roots satisfy the condition x ≥ 0, so they also satisfy the original equation.
Under the condition x < 0, the modulus of the equation expanded with a minus, resulting in roots -2 and -3. Both roots satisfy the condition x < 0, so they also satisfy the original equation.
Answer: 3, 2, -2 and -3.
Converting an equation with a modulus into a set
Most elementary equations with a modulus can be solved by reducing them to a so-called set of equations.
We will call elementary those equations with modulus in which the left part is a modulus of some expression and the right part is a number. For example, |x| = 3 or |2x - 1| = 3.
Solve our very first equation |x - 2| = 5 by reducing it to a set of equations. The roots of this equation were the numbers 7 and -3. This equation is also considered elementary.
If you expand the module |x - 2| with the plus sign, the equation |x - 2| = 5 will look like x - 2 = 5.
If we expose the module |x - 2| with the minus sign, the equation |x - 2| = 5 will take the form -(x - 2) = 5, that is -x + 2 = 5.
We see that the equation |x - 2| = 5 results in two equations: x - 2 = 5 and -x + 2 = 5. And each of the equations has its own root. The equation x - 2 = 5 has a root of 7, and the equation -x + 2 = 5 has a root of -3.
Write the equations x - 2 = 5 and -x + 2 = 5 and join them with a square bracket:
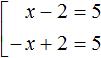
This kind of recording is called a set of equations.
A set of equations is several equations joined by a square bracket and having many solutions that satisfy at least one of the equations in the set.
So, number 7 is a solution to the 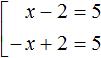 set because this number satisfies the first equation x - 2 = 5.
set because this number satisfies the first equation x - 2 = 5.
The number -3 is also a solution to this set because it satisfies the second equation -x + 2 = 5.
Together, the numbers 7 and -3 form the set of solutions of this set.
Unlike a system of equations, a set consists of equations that are independent of each other. For each equation in the set, the value of variable x will be different. And in a system of equations, the value of the variable x satisfies both the first equation and the second equation.
Solving a set of equations means finding a set of solutions that satisfy at least one of the equations in the set.
Let's solve each equation of the 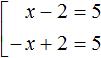 set separately. These are ordinary linear equations that are easy to solve:
set separately. These are ordinary linear equations that are easy to solve:
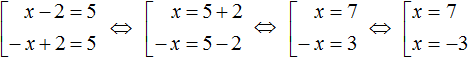
The symbol ⇔ as previously stated means equivalence. In this case it indicates that all resulting sets are equivalent to each other.
So we obtained roots 7 and -3. Since these two numbers are solutions to the 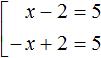 set, they are also solutions to the equation |x - 2| = 5.
set, they are also solutions to the equation |x - 2| = 5.
The initial set can include the conditions according to which the module was solved. In this case, each equation together with its condition is framed with the system sign.
Supplement the previous set of conditions, according to which the modulus was solved. To the first equation x - 2 = 5 add the condition x - 2 ≥ 0, and to the second equation -x + 2 = 5 add the condition x - 2 < 0
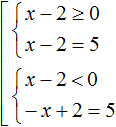
The solution to each equation must satisfy its own condition. Therefore, the conditions and equations are framed with a system sign.
Solve the resulting set with conditions. The conditions are inequalities that can also be solved:
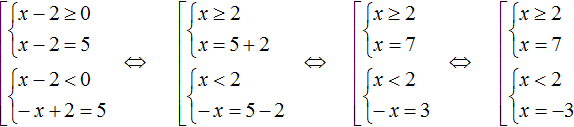
In the first case we got a root of 7, which satisfies its condition x ≥ 2. In the second case we got a root of -3, which satisfies its condition x < 2.
Don't be afraid of these entries. This is just a detailed solution, showing what came from where. Most of the time the solution can be written in a shorter form.
There is a scheme for combining an equation of the form |x| = a. This scheme looks like this:
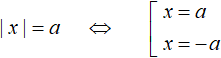
This scheme makes it easy to reduce an equation with a modulus to a set. This scheme can be read as, "If expression |x| equals a, then the submodular expression equals a or -a".
A square bracket in set replaces the word "or".
For example, the equation |x| = 5 can be reduced to a set by reasoning that if the expression |x| is 5, then the submodular expression is 5 or -5.
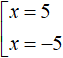
As for our previous example, if |x - 2| equals 5, then the submodular expression equals 5 or -5
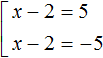
This is the same set as last time. Verify this by multiplying both parts of the second equation by -1.
In equations where there is a modulus on the left and a number on the right, we will more often use this way of writing the set. It allows you not to resort to the modulo exponentiation rule, but to obtain the set at once.
But remember that this scheme will only work for equations of the form |x| = a. That is, for equations that have a modulus on the left and a number on the right.
Example 2. Solve the equation |2x - 1| = 3
Solution
This equation has a modulus on the left and a number on the right. So it can be converted to a set using scheme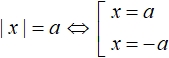
If the expression |2x - 1| equals 3, then the submodular expression 2x - 1 equals 3 or -3
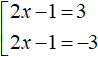
Now let's solve each equation of the set separately:
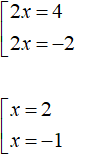
Answer: 2 and -1.
Example 3. Solve the equation |x + 2| - 3 = 8
Solution
In some cases, before the original equation can be reduced to a set, it must be simplified.
So, in this case, -3 should be moved to the right side by changing the sign:
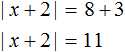
We obtain the equation |x + 2| = 11. If |x + 2| equals 11, then the submodular expression x + 2 equals 11 or -11
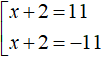
Let us solve this set:
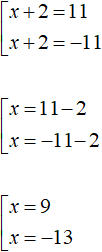
Answer: 9 and -13.
Example 4. Solve the equation 4|x| + 4 = 2|x| + 10
Solution
Move 2|x| from the right side to the left side, and move 4 from the left side to the right side:
4|x| − 2|x| = 10 − 4
2|x| = 6
Divide both parts of the resulting equation by 2. Then we get a simple equation with a modulus:
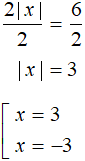
Answer: 3 and -3.
Example 5. Solve the equation ![]()
Solution
If |2 - 5x2| equals 3, then the submodular expression 2 - 5x2 equals 3 or -3
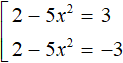
In both equations, move 2 to the right side, changing the sign:
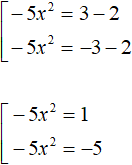
In the first equation, divide both parts by -5. In the second equation, divide both parts by -5. Then we obtain two quadratic equations
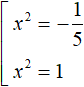
The first equation has no roots because the square of any number is positive, and in this case it equals a negative number. The roots of the second equation are the numbers 1 and -1 because the second degree of these numbers is equal to one.
Answer: 1 and -1.
Example 6. Solve the equation |x + 6| + 4x = 5
Solution
This equation is not an equation of the form |x| = a, so you can not use the scheme 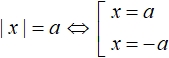 .
.
To reduce this equation to a set, you must first solve its modulus, then write down the set of the resulting equations.
Let us disclose the module |x + 6|
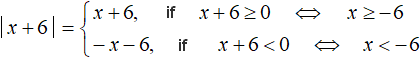
If x + 6 ≥ 0 , then the modulus will expand with the plus sign and then the original equation will look like x + 6 + 4x = 5
If x + 6 < 0 , then the modulus opens with a minus sign and then the original equation will look like -x - 6 + 4x = 5. We obtain the following set:
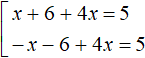
A further solution is elementary:
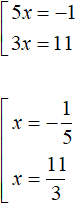
Of the roots found, only ![]() is a root of the original equation because it satisfies the condition x ≥ -6. And root
is a root of the original equation because it satisfies the condition x ≥ -6. And root ![]() is not a root of the equation because it does not satisfy the condition x < -6.
is not a root of the equation because it does not satisfy the condition x < -6.
Answer: ![]()
The simplest kind
The simplest kind of equation with a module looks like this:
| x | = a
where x - is the root of the equation, a - is an arbitrary number large or equal to zero. That is, a ≥ 0
If the condition a ≥ 0 is not satisfied, then the equation |x|= a has no roots. This follows from the definition of modulus. Indeed, modulus is always non-negative.
Here are some examples of equations of the form |x| = a
Example 1. Solve the equation |x| = 2
Solution
In this case it is immediately obvious that the roots are the numbers 2 and -2. For if we substitute these numbers instead of x, we obtain the correct equality: |-2| = 2 and |2| = 2. The solution to this equation can be written down by combining it into a set:
"If expression |x| equals 2, then the submodular expression x equals 2 or -2"
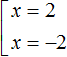
Answer: 2 and -2
Example 2. Solve the equation |−x| = 4
Solution
If the expression |-x| is 4, then the submodular expression is 4 or -4
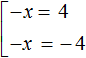
Multiply both equations by -1
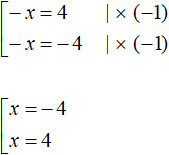
Answer: −4 and 4.
Example 3. Solve the equation |x| = −7
In this case there are no roots, because the modulus is always non-negative. And in this case, modulus is a negative number.
If an equation with modulus has no roots, it is usual to write that x belongs to an empty set:
x ∈ ø
Recall that an empty set is a set that has no elements.
Module inside a module
Consider the equation:
![]()
In this equation, there is a module on the left, which in turn contains another module within it, and there is a number on the right side of the equation. This kind of equation with a modulus can be solved by combining it into a set using the scheme we discussed earlier:
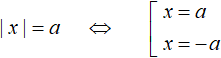
In our case, if expression ![]() is 9, then the submodular expression |2 + x| + 3 is 9 or -9
is 9, then the submodular expression |2 + x| + 3 is 9 or -9
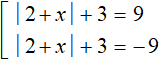
In the resulting set there are two equations with a module. These equations, too, should be combined into a set. But first let us simplify these equations. In the first and second equations move 3 to the right side, changing the sign. Then we get:
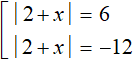
Now let us put these equations together. The first equation will decompose into the following set:
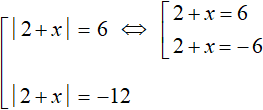
Immediately solve the set of 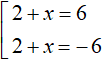 . The first root is 4, the second is -8.
. The first root is 4, the second is -8.
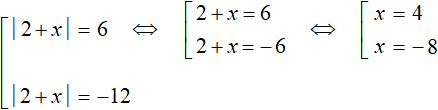
Now solve the second equation |2 + x| = -12. But we notice that its right side is a negative number. This equation has no roots, because the modulus cannot equal a negative number.
So equation ![]() has roots 4 and -8. Check these roots by substituting them into the original equation
has roots 4 and -8. Check these roots by substituting them into the original equation ![]()
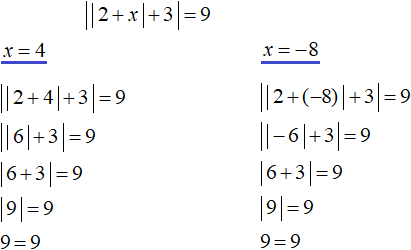
In this case, both roots satisfy the original equation.
Answer: 4 and -8.
In general, an equation with a module containing another module is also solved in different ways. Which way to use depends on the equation itself. Solve the following equation, for example:
![]()
Here we can no longer use the scheme 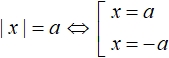 because not only the modulus is on the left, but also the variable x. Of course, the variable x can be moved to the right side, and then it will be possible to reduce this equation to a set:
because not only the modulus is on the left, but also the variable x. Of course, the variable x can be moved to the right side, and then it will be possible to reduce this equation to a set:
![]()
But then the variable x appears on the right side, which will need to be further constrained so that the right side of the equation does not become negative. We will consider this way of solving the equation later. For now, we will solve the original equation using the modulus expansion rule.
In order to solve the modules of the equation, we first need to determine where the outer and inner modules are.
In equation ![]() , the outer module is the all-left part
, the outer module is the all-left part ![]() , and the inner module is expression
, and the inner module is expression ![]()
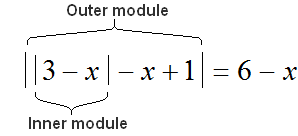
The value of the outer module depends on the inner module, and the outer module will expand based on the result of calculating its submodule content.
For example, if x = 3, then the internal module |3 - x| will drop to 0, and the whole submodule value of the external module will become -2. This means that the outer module will expand with a minus.
||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
And if for example x = -2, then the internal module |3 - x| will take the value 5, and as a result the entire submodular expression of the external module will become 8. This means that the outer module will expand with a plus:
||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Therefore we will begin the solution by solving the inner modulus.
If the inner module expands with plus, that is, if 3 - x ≥ 0 (which is equivalent to the inequality x ≤ 3), then the original equation will take the form:
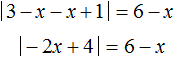
Now the equation has only an outer module. Solve it by solving the modulus:
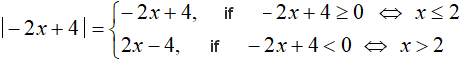
If -2x + 4 ≥ 0, then:

Now we are interested only in those values of x at which the internal modulus expands with plus, and this will happen if x ≤ 3. Therefore, for clarity, next to the found root it is indicated that it satisfies the condition x ≤ 3
We solve next. If -2x + 4 < 0, then:

Despite the fact that both found roots satisfy the equation |-2x+4|=6-x, we exclude root ![]() from the solutions, because we are now interested only in those values of x at which the inner module of the original equation expands with a plus. Therefore, next to the root
from the solutions, because we are now interested only in those values of x at which the inner module of the original equation expands with a plus. Therefore, next to the root ![]() it is indicated that it does not satisfy the condition x ≤ 3.
it is indicated that it does not satisfy the condition x ≤ 3.
So, if the internal modulus is expanded with plus, the original equation takes the form |-2x + 4| = 6 - x and the root of this equation is the number -2.
Now solve the original equation for the case when the inner module expands with a minus, that is, when 3 - x < 0 (which is equivalent to the inequality x > 3). The inner module will expand minus for all values of x greater than 3.
If the inner module expands with minus, the original equation will look like this:
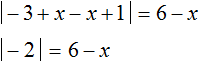
The modulus of -2 equals 2. Then we get the simplest linear equation, the root of which is 4

We obtained a root of 4, which satisfies the condition x > 3.
As a result, the roots of the equation are -2 and 4.
Answer: 2 and 4.
Example 3. Solve the equation ||x - 1| - 7| = 10
Solution
There is a module on the left and a number on the right, so you can apply the scheme: 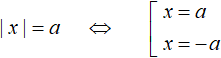
In this case, if the expression ||x - 1| - 7| is 10, then the submodular expression |x - 1| - 7 is 10 or -10. This results in a set of two equations:
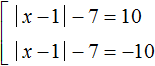
Simplify the resulting equations. Move the number -7 in both equations to the right side, changing the sign:
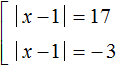
The second equation has no roots. The first equation will decompose into a set of 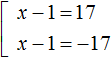 , whose roots are 18 and -16.
, whose roots are 18 and -16.
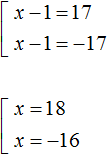
Answer: 18 and -16.
Let us solve the same equation using the expansion of modules. We start with the inner modulus.
If x - 1 ≥ 0 (which is equivalent to x ≥ 1), then the original equation will take the form:
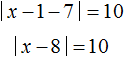
Solve the resulting equation by expanding the modulus:
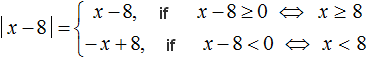
Then we solve the equation for the cases when x - 8 ≥ 0 and x - 8 < 0
![]()
Now we are interested in the values at which the internal modulus of the original equation expands with a plus. This will be if x ≥ 1. This condition is satisfied only by value 18, so we marked it with a green check mark for clarity.
Now solve the original equation for the case where the inner module expands with a minus, that is, when x - 1 < 0 (or which is equivalent to the inequality x < 1).
If x - 1 < 0, then the original equation will take the form:
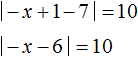
Solve the resulting equation by expanding the modulus:
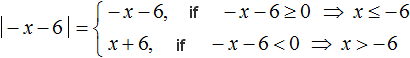
Then we solve the equation for the cases when -x - 6 ≥ 0 and -x - 6 < 0

Of the roots found, only -16 satisfies the condition x < 1.
As a result, the roots of the equation ||x - 1| - 7| = 10 are the numbers 18 and -16.
You can see that this equation was solved easier and faster with the help of scheme 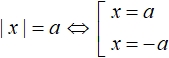 than with the modulo expansion method.
than with the modulo expansion method.
On the left is a module and on the right an expression with a variable
Solve the following equation with a module:
|4x − 3| = 3x
The scheme also applies here:
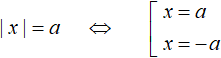
That is, if the expression |4x - 3| equals 3x, then the submodular expression 4x - 3 must equal 3x or -3x.
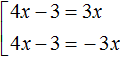
But the original equation contains the variable x not only under the modulo sign, but also in the right-hand side. We do not yet know what value x will take. If x has a negative value, then the right hand side will be completely negative. In this case there will be no roots, because modulus cannot equal a negative number.
Therefore, if we want to solve this equation, we must additionally introduce a restriction in the form of the condition 3x ≥ 0. This would mean that the right side of the equation |4x - 3| = 3x must be greater than or equal to zero:
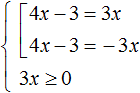
The set and the condition are framed with the system sign, because the solutions of the set must satisfy the condition 3x ≥ 0.
So we solve the set. The condition 3x ≥ 0 is an inequality which can also be solved:
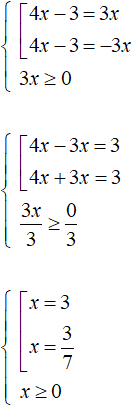
The resulting roots can be substituted into the condition x ≥ 0 and see if it holds. If it holds, then the found roots satisfy the equation. In this case, by substituting both roots into the inequality, it is satisfied. Checking also shows that the roots satisfy the equation:
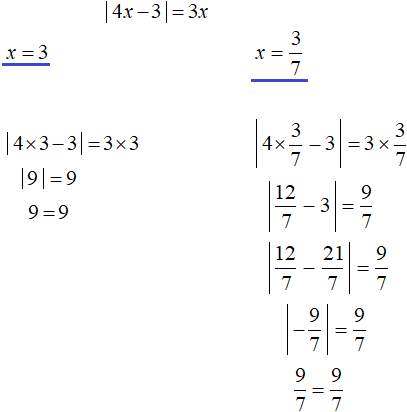
Example 2. Solve the equation |2x - 1| = 5x - 10
Solution
Solve this equation the same way as the previous one. Introduce a condition requiring that the right-hand side is greater than or equal to zero:
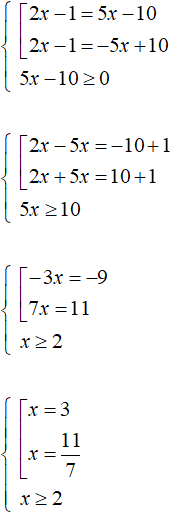
In this case only value 3 satisfies the condition x ≥ 2. It is also the only root of the original equation. A check shows this:
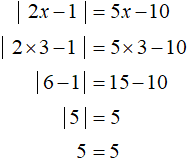
And the number ![]() does not satisfy the condition x ≥ 2 and is not the root of the original equation. A check also shows this:
does not satisfy the condition x ≥ 2 and is not the root of the original equation. A check also shows this:
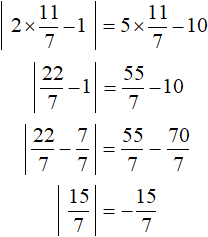
We see that the modulus has become a negative number, and this contradicts the definition of modulus and our condition x ≥ 2.
Example 3. Solve the equation ![]()
Solution
We solved this equation when we learned how to solve equations with a modulus within which there is another modulus. Now this equation can be solved by combining it into a set.
Let's start by moving x to the right side, changing the sign:
![]()
Now let us reduce this equation to a set. Additionally, we introduce a condition in the form of the inequality 6 - x ≥ 0
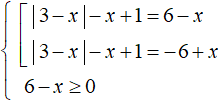
Leave the modulus in the left part of the first equation, and move the remaining terms to the right part. Do the same with the second equation. We will also solve the inequality 6 - x ≥ 0, it will allow us to check at the end to find the roots:
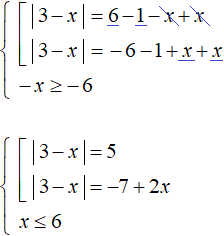
Let us solve the first equation. It will decompose into the following set:
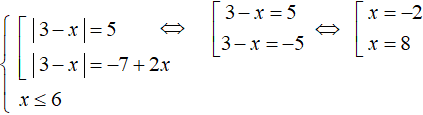
We got roots -2 and 8. Of these, only -2 satisfies the condition x ≤ 6.
Now solve the second equation. This is an equation containing a variable in the right part. When we aggregate it into a set, add the condition -7 + 2x ≥ 0
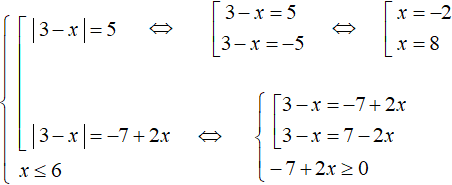
The rest is elementary:
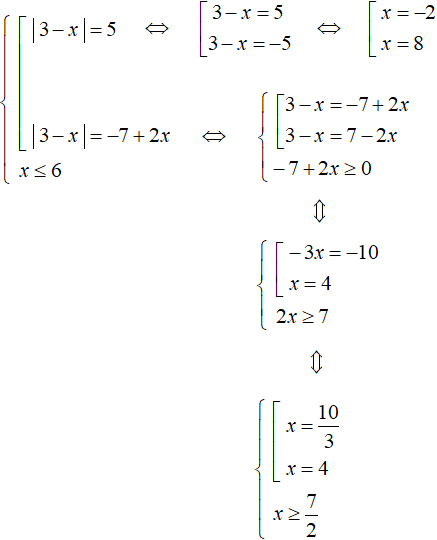
When solving the second equation we got roots ![]() and 4. Before checking them against the condition x ≤ 6, you should check them against the condition
and 4. Before checking them against the condition x ≤ 6, you should check them against the condition ![]() under which the equation |3 - x| = -7 + 2x was solved. Condition
under which the equation |3 - x| = -7 + 2x was solved. Condition ![]() satisfies only root 4.
satisfies only root 4.
As a result, the roots of the original equation ![]() are -2 and 4.
are -2 and 4.
Example 4. Solve the equation |4x + 20| = -6x
Solution
At first glance it would seem that this equation has no solutions because the right-hand side is negative. But this is not exactly true. The right-hand side contains a variable x which can take a negative value or zero, and this would cause the right-hand side to become positive or equal to zero. And such an equation has a right to exist.
In this case, we solve this equation by combining it into a set. But we will specify that the right-hand side must be greater than or equal to zero:
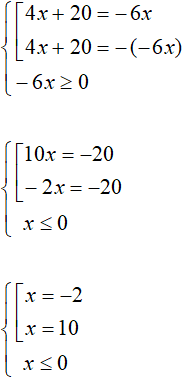
Of the roots found, only root -2 satisfies the original equation. It also satisfies our condition x ≤ 0.
Answer: -2.
When both parts are modules
Solve the following equation:
|x + 7| = |1 + 3x|
Both parts of this equation are modules. Let us expand these modules. We will take into account all possible cases of their expansion.
Case 1. If x + 7 ≥ 0 and 1 + 3x ≥ 0, then the modules in both parts will expand with a plus sign and then the original equation will take the form:
x + 7 = 1 + 3x
This is the simplest linear equation. Let's solve it:
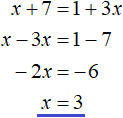
Case 2. If x + 7 < 0 and 1 + 3x < 0, then the modules in both parts will expand with a minus sign and then the original equation will take the form:
−(x + 7) = −(1 + 3x)
Open the brackets, and we get:
−x − 7 = −1 − 3x
Note that if we multiply both parts of this equation by -1, we get the equation x + 7 = 1 + 3x. And this equation we obtained as a result of expanding the moduli with the plus sign.
That is, the equations x + 7 = 1 + 3x and -x - 7 = -1 - 3x are equivalent, so they have the same roots. Let us check this by solving the equation
−x − 7 = −1 − 3x
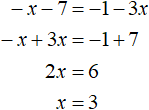
Therefore, if you expand the modules with the plus sign, there is no need to expand them with the minus sign, because in both cases you get equations that have the same roots.
Case 3. The next case is when x + 7 ≥ 0 and 1 + 3x < 0. Then the original equation will take the form x + 7 = -1 - 3x. Find the root of this equation:
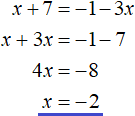
Case 4. And the last case is when x + 7 < 0 and 1 + 3x ≥ 0. Then the equation is -x - 7 = 1 + 3x. If we multiply this equation by -1, we get the equation x + 7 = -1 - 3x. And this is the equation we got when we considered the previous case (the case of x + 7 ≥ 0 and 1 + 3x < 0).
Hence, the equation -x - 7 = 1 + 3x is equivalent to the previous equation x + 7 = -1 - 3x. We will see that by solving the equation -x - 7 = 1 + 3x
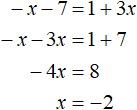
So by expanding the left side with a plus sign and the right side with a minus sign, there is no need to expand the left side with a minus sign and the right side with a plus sign, because in both cases we get equations that have the same roots.
In general, if in an equation both parts are modules as in this example, the equation can be reduced to the following set:
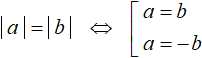
In this construction the equation of the form |a| = |b| is reduced to a set of two equations a = b and a = -b. It can be seen that the first equation is obtained by expanding both modules with a plus sign, and the second equation is obtained by expanding the module |a| with a plus sign and the module|b| with a minus sign.
Important. This scheme only works when both parts are modules without extraneous terms. Simply put, if an equation such as |a| = |b| + c is given, the above scheme cannot be used.
Example 2. Solve the equation |2 - 3x| = |x + 5|
Solution
Both parts of this equation are modules. Let us use the scheme:
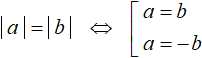
We will have a set of two equations. In the first equation both modules will be expanded with a plus sign, in the second equation the module |2 - 3x| will be expanded with a plus sign, and the module |x + 5| with a minus sign:
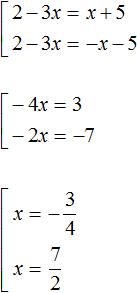
Let's make a check:
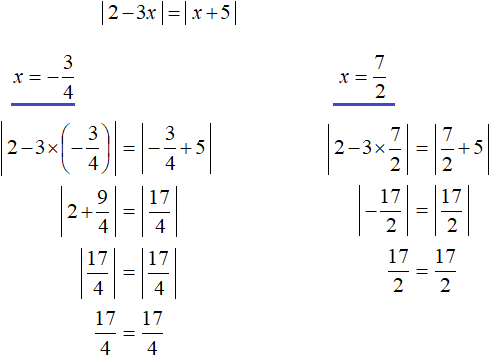
Answer: ![]() and
and ![]()
Example 3. Solve the equation |x2 − 13x + 35|=|35 − x2|
Solution
Both parts of this equation are modules. Let us use the scheme:
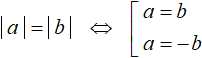
We will have a set of two equations. In the first equation, both modules will be expanded with a plus sign. In the second equation, the module |x2 − 13x + 35| will be expanded with a plus sign, and the module |35 − x2| with a minus sign:
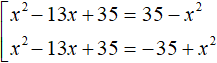
Let us give like terms in both equations:
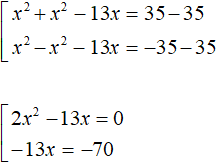
The first equation is an incomplete square. Solve it by taking x out of the brackets. The second equation is solved elementary:
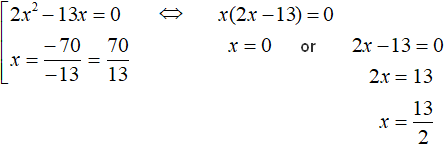
Answer: ![]() ,
, ![]() , 0.
, 0.
When the solution is a numeric interval
It is not uncommon to have to solve an equation with a module, where the roots are not one or two numbers, but a numeric interval. This is, for example, the equation:
|5x + 3| = −5x − 3
Let's expand the modulus of this equation:
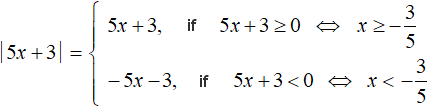
If you expand the modulus with the plus sign, you get the equation 5x + 3 = -5x - 3. Solve it:
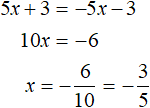
And if you expand the modulus with a minus sign, you get the equation -5x - 3 = -5x - 3. In this equation both parts are the same, so this equation is an identity. It will be true for any value of x. So the roots of the equation -5x - 3 = -5x - 3 are all numbers from minus infinity to plus infinity:
x ∈ (−∞; +∞)
But we must remember the conditions under which the modules were expanded. In the first case we got the root of ![]() . It will only be true if the condition is
. It will only be true if the condition is ![]() . This condition is satisfied. A check also shows that the root is true:
. This condition is satisfied. A check also shows that the root is true:
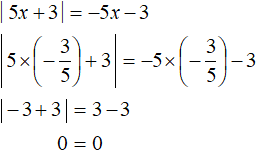
So one of the roots of the equations is ![]()
In the second case we got a set of roots from minus infinity to plus infinity. But this will be true only under the condition that ![]()
For example, if we take any number from the interval (-∞; +∞), but which will not satisfy the condition ![]() , then this number will not convert our equation to a true equality.
, then this number will not convert our equation to a true equality.
For example, the number 2 belongs to the interval (-∞; +∞), but does not satisfy the condition ![]() , so the number 2 is not the root of the original equation. A check will also show this:
, so the number 2 is not the root of the original equation. A check will also show this:
And if you take for example the number -5, it will belong to the interval (-∞; +∞) and satisfy the condition ![]() , which means it will convert the original equation into a correct equality:
, which means it will convert the original equation into a correct equality:
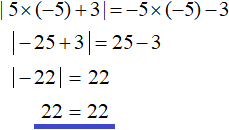
Therefore the answer must be written so that both conditions ![]() and
and ![]() are satisfied. For clarity, let us draw a coordinate line and denote it as x
are satisfied. For clarity, let us draw a coordinate line and denote it as x

Mark on it our first root ![]()

By expanding the module with the minus sign and solving the resulting equation, we obtained in the answer the set of all numbers from minus infinity to plus infinity, but the condition ![]() was given. So the more accurate answer in this case would be this:
was given. So the more accurate answer in this case would be this:
The roots of the equation -5x - 3 = -5x - 3 under condition ![]() are all numbers from minus infinity to
are all numbers from minus infinity to ![]()
So on the coordinate line you should shade the area to the left of the number ![]() . They will illustrate numbers smaller than
. They will illustrate numbers smaller than ![]()

The number ![]() is also the correct root of the original equation. It was obtained by exposing the modulus with the plus sign. Therefore on the coordinate line the empty circle should be shaded. Thus we will include the number
is also the correct root of the original equation. It was obtained by exposing the modulus with the plus sign. Therefore on the coordinate line the empty circle should be shaded. Thus we will include the number ![]() in the set of solutions:
in the set of solutions:

Then the final answer would look like this:
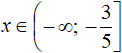
Answer: 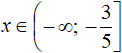
Also, you can solve this equation by reducing it to a set, additionally specifying that the right side must be greater than or equal to zero:
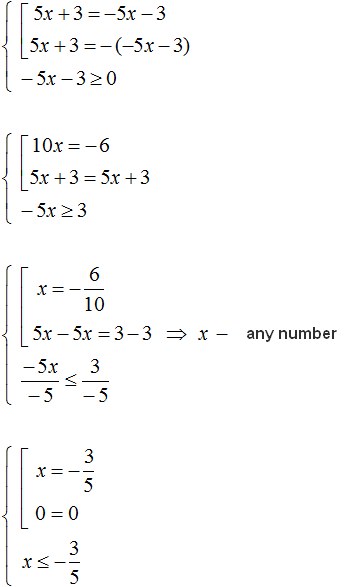
Example 2. Solve the equation |2x - 3| = 3 - 2x
Solution
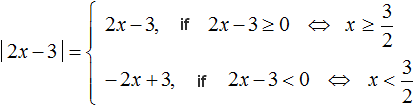
Solve the original equation for the cases when 2x - 3 ≥ 0 and 2x - 3 < 0
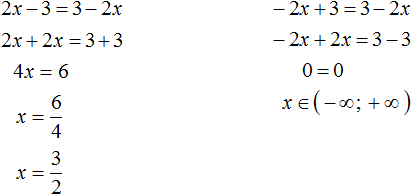

Answer: 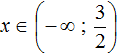
Using the coordinate line
Let's look at another way to solve elementary equations with modulus - using a coordinate line. This method is rarely used, but it doesn't hurt to know about it.
Solve our very first equation |x - 2| = 5 using the coordinate line. Recall that the roots of this equation were the numbers 7 and -3.
The modulus is the distance from the origin to point A. Or the distance between two numbers on a coordinate line.
The distance between two numbers is expressed as the difference |x1 − x2|, where x1 is the first number, x2 is the second number.
If you look closely at the equation |x - 2|= 5, you can see that its left side is the distance from x to 2 (or from 2 to x) and this distance is 5. Mark the number x and the number 2 on the coordinate line
![]()
The right side of the equation |x - 2|= 5 indicates that the distance from x to 2 is five units:

If the distance from x to 2 is 5, then the distance from 2 to x is also 5. This allows you to count five integer steps from number 2 to x and thus find the value of x

You can see that after counting five steps to the left we get to the point with coordinate -3. And this is one of the roots we found for the equation |x - 2|= 5.
But five whole steps from number 2 can be counted not only to the left, but also to the right:

If we count five whole steps to the right, we get to the point with coordinate 7. This was also the root of the equation |x - 2|= 5

Several modules in one part
Let's solve the following equation:
|x − 5| − |x| = 1
This equation contains two modules on the left side. To solve this equation you need to solve its modules. Consider each of the cases:
- when both modules are greater than or equal to zero;
- when both modules are less than zero;
- when the first module is greater than or equal to zero, and the second module is less than zero;
- when the first modulus is less than zero and the second modulus is greater than or equal to zero.
We will not comment on each case, but give the solution at once:
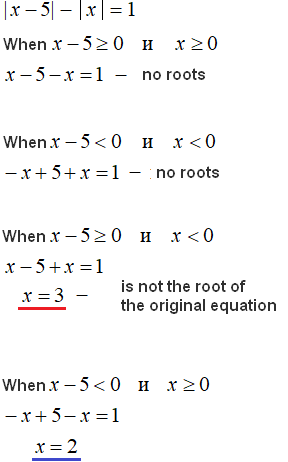
The first two cases yielded no roots. In the third case, a root of 3 was found, but it does not satisfy the conditions x - 5 ≥ 0 and x < 0, so it is not a root of the original equation.
In the fourth case, a root of 2 was found which satisfies the conditions x - 5 < 0 and x ≥ 0. It also satisfies the original equation.
It is noticeable that this way of solving the equation is inconvenient. If there are three or four or more modules in the equation, we would have to consider many more cases. A person can get confused and forget to consider some of the cases, and the equation will not be solved completely.
This is why it is more convenient to solve such an equation as in this example by the method of intervals. We will talk about this in the next lesson.
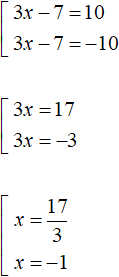
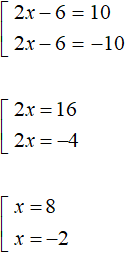
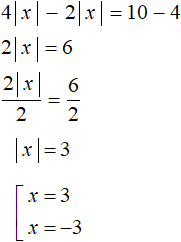

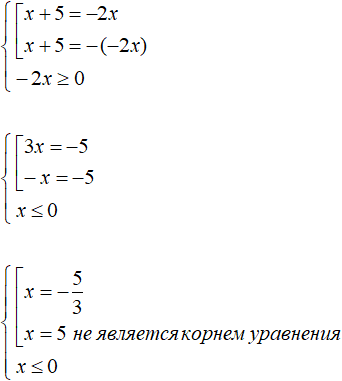
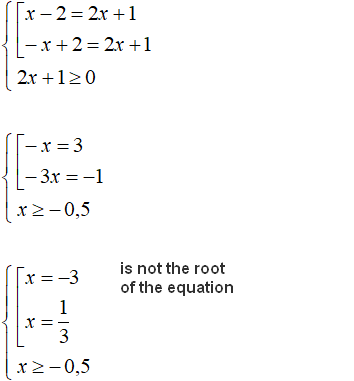
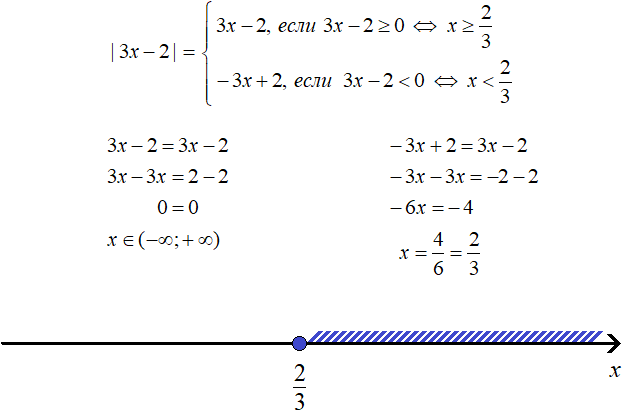
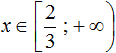 .
.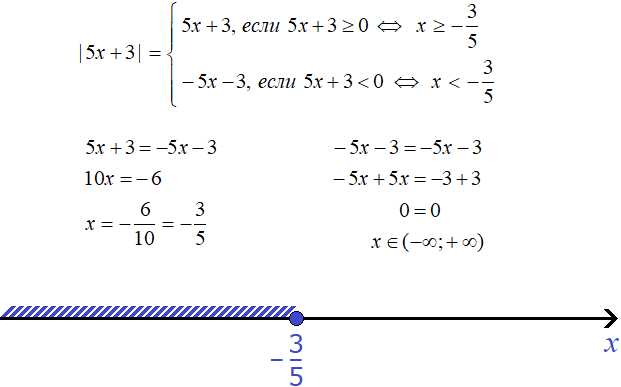
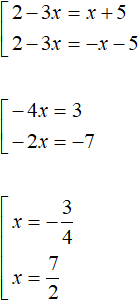
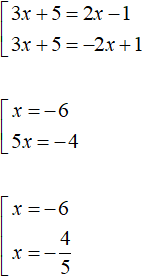
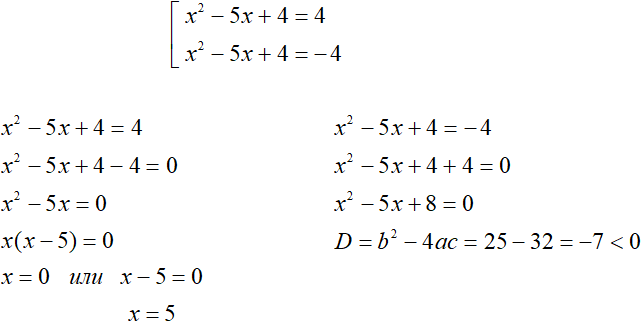
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.