This material contains geometric shapes with measurements. The measurements shown are approximate and may not be the same as in real life.
The perimeter of a geometric figure
The perimeter of a geometric figure is the sum of all its sides. To calculate the perimeter, measure each side and add up the results.
Calculate the perimeter of the following figure:
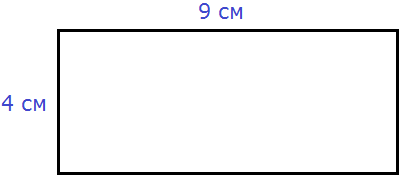
This is a rectangle. We will talk about this figure in more detail later. For now we just calculate the perimeter of this rectangle. Its length is 9 cm and its width is 4 cm.
A rectangle has opposite sides that are equal. This can be seen in the diagram. If the length is 9 cm and the width is 4 cm, then the opposite sides are 9 cm and 4 cm, respectively:
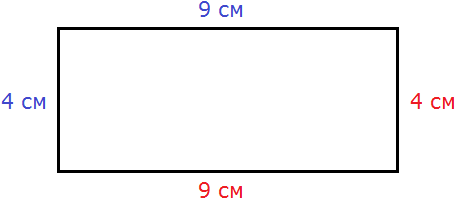
Let's find the perimeter. To do this, add all the sides. They can be added in any order, because the sum does not change when the places of the summands are rearranged. The perimeter is often denoted by the capital Latin letter P. Then we get:
P = 9 cm + 4 cm + 9 cm + 4 cm = 26 cm.
Since a rectangle has equal opposite sides, finding the perimeter is written shorter by adding the length and width and multiplying it by 2, which would mean "repeat length and width twice".
P = 2 × (9 + 4) = 18 + 8 = 26 cm.
A square is the same as a rectangle, but with all sides equal. For example, find the perimeter of a square with a side of 5 cm. The phrase "with a side of 5 cm" should be understood as "the length of each side of the square is 5 cm".
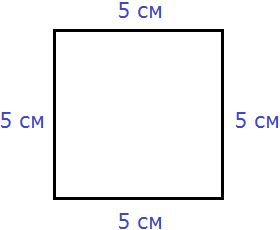
To calculate the perimeter, add up all the sides:
P = 5 cm + 5 cm + 5 cm + 5 cm = 20 cm
But since all sides are equal, the perimeter calculation can be written as a product. The side of the square is 5 cm, and there are 4 sides. Then this side equal to 5 cm must be repeated 4 times
P = 5 cm × 4 = 20 cm
The area of a geometric figure
The area of a geometric figure is a number that characterizes the size of that figure.
It should be clarified that in this case we are talking about the area on a plane. A plane in geometry is any flat surface, for example: a sheet of paper, a plot of land, the surface of a table.
An area is measured in square units. Square units refer to squares whose sides are equal to one. For example, 1 square centimeter, 1 square meter, or 1 square kilometer.
To measure the area of a shape means to find out how many square units it contains.
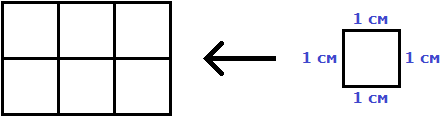
For example, the area of the following rectangle is three square centimeters:

This is because this rectangle contains three squares, each with a side equal to one centimeter:

On the right is a square with a side of 1 cm (it is the square unit in this case). If we look at how many times this square enters the rectangle represented on the left, we find that it enters it three times.
The next rectangle has an area equal to six square centimeters:

This is because this rectangle contains six squares, each with a side equal to one centimeter:
Let's say you need to measure the area of the next room:

Let's determine in what squares we will measure the area. In this case, it is convenient to measure the area in square meters:
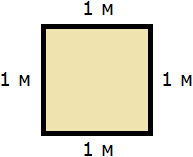
So, our task is to determine how many such squares with a side of 1 m are contained in the original room. Let us fill the whole room with this square:
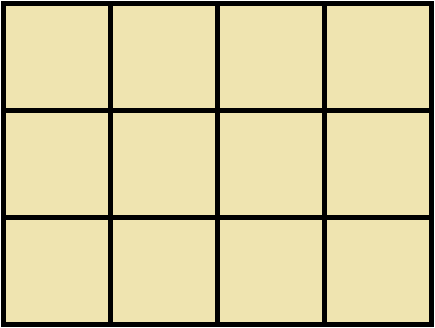
We see that a square meter is contained in the room 12 times. So the area of the room is 12 square meters.
Square of a rectangle
In the previous example, we calculated the area of the room by sequentially checking how many times it contains a square whose side is one meter. The area was 12 square meters.
The room was a rectangle. The area of the rectangle can be calculated by multiplying its length and width.
To calculate the area of a rectangle, multiply its length and width.
Let's go back to the previous example. Suppose we measured the length of the room with a tape measure and it turned out to be 4 meters long:

Now let's measure the width. Let it be three meters:
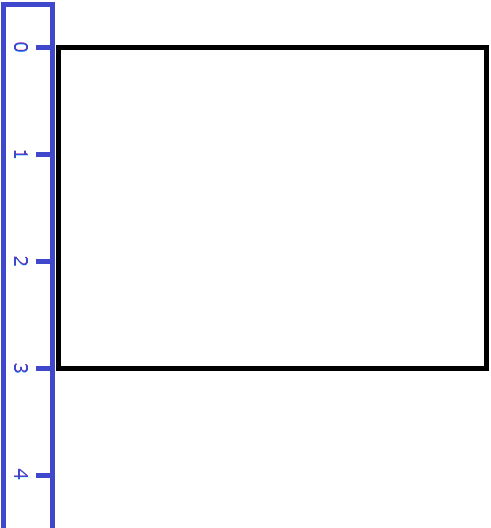
Multiply the length (4 m) by the width (3 m).
4 × 3 = 12
Like the last time, we get twelve square meters. This is because by measuring the length, we find out how many times we can fit a square with a side equal to one meter into that length. Let's put four squares into that length:
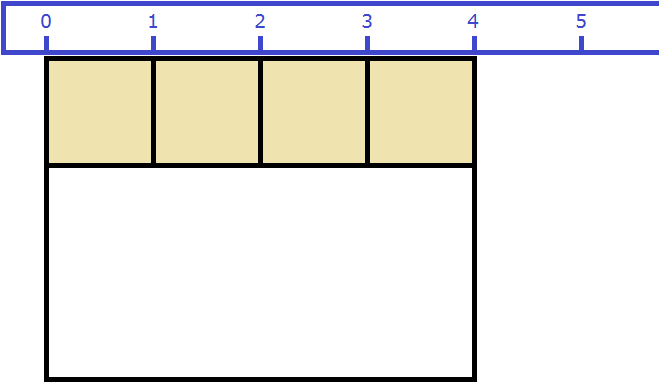
Then we determine how many times we can repeat this length with the stacked squares. This we find out by measuring the width of the rectangle:
Square footage
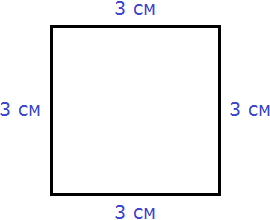
A square is the same as a rectangle, but with all sides equal. For example, the following picture shows a square with a side of 3 cm. The phrase "a square with a side of 3 cm" means that all sides are equal to 3 cm.
The area of a square is calculated in the same way as the area of a rectangle - the length is multiplied by the width.
Calculate the area of a square with a side of 3 cm. Multiply the length of 3 cm by the width of 3 cm.
3 × 3 = 9
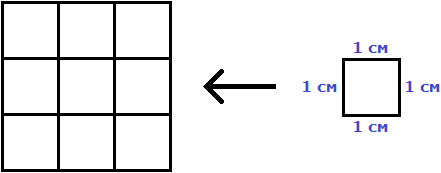
In this case we wanted to know how many squares with side 1 cm are contained in the original square. The original square contains nine squares with a side of 1 cm. Indeed it does. A square with side 1 cm, is included in the original square nine times:
By multiplying the length by the width, we get the expression 3 × 3, and this is the product of two identical factors, each of which is equal to 3. That is, the expression 3 × 3 is the second power of the number 3. So the process of calculating the area of the square can be written as the power of 32.
Therefore, the second power of a number is called the square of a number. By calculating the second power of a number a, one finds the area of a square with side a. The operation of raising a number to the second power is otherwise called squaring.
Designations
The area is denoted by a capital Latin letter S (Square). Then the area of a square with side a cm will be calculated by the following rule
S = a2
where a is the length of the side of the square. The second power indicates that two identical factors, namely length and width, are multiplied. Earlier it was said that all sides of the square are equal, so the length and width of the square, expressed through the letter a, are equal.
If the task is to determine how many squares of side 1 cm are contained in the original square, then cm2 should be specified as the units of area. This designation replaces the phrase "square centimeter".
For example, let's calculate the area of a square with a side of 2 cm.

So, a square with a side of 2 cm, has an area equal to four square centimeters:

If the task is to determine how many squares with a side of 1 m are contained in the original square, you should specify m2 as the unit of measure. This designation replaces the phrase "square meter".
Calculate the area of a square with a side of 3 meters
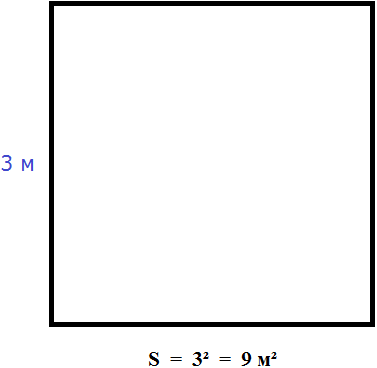
So, a square with a side of 3 m, has an area equal to nine square meters:
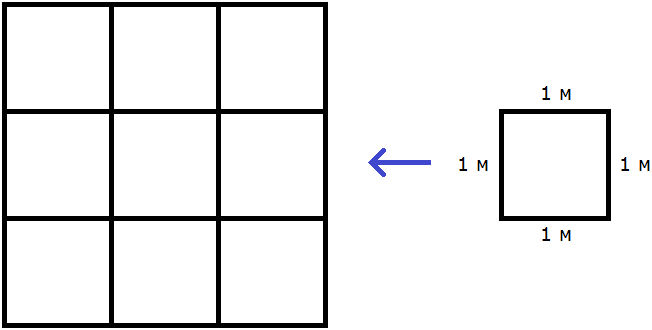
Similar notations are used when calculating the area of a rectangle. But the length and width of a rectangle can be different, so they are denoted by different letters, for example a and b. Then the area of a rectangle with length a and width b is calculated by the following rule:
S = a × b
As in the case of the square, the units of measurement of the area of a rectangle can be cm2, m2, km2. These designations replace the phrases "square centimeter", "square meter", "square kilometer", respectively.
For example, let's calculate the area of a rectangle 6 cm long and 3 cm wide
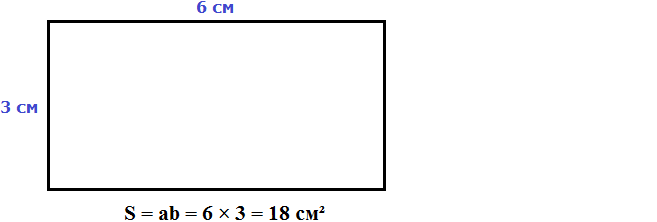
So a rectangle 6 cm long and 3 cm wide has an area equal to eighteen square centimeters:
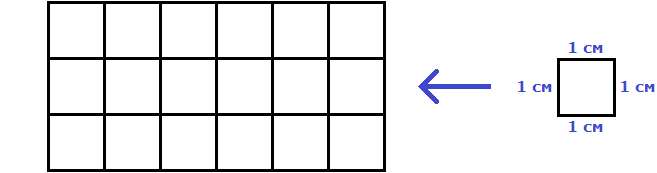
It is acceptable to use the phrase "square units" as a unit of measure. For example, the notation S = 3 square units means that the area of a square or rectangle is equal to three squares, each of which has a unit side (1 cm, 1 m or 1 km).
Conversion of area units
Units of area can be converted from one unit of measure to another. Let's look at a few examples:
Example 1. Express 1 square meter in square centimeters.
1 square meter is a square with a side of 1 meter. That is, all four sides have a length equal to one meter.
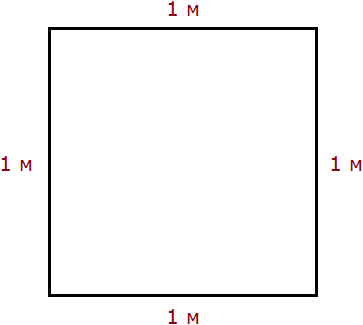
But 1 m = 100 cm. Then all four sides also have a length equal to 100 cm
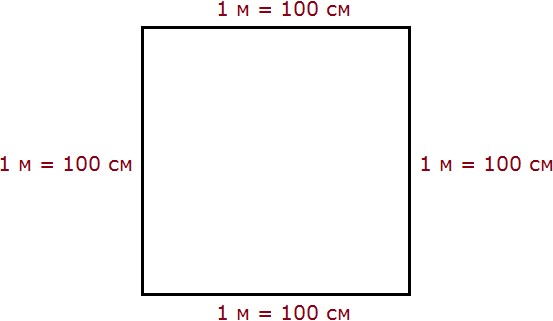
Let's calculate the new area of this square. Multiply the length of 100 cm by the width of 100 cm or square the number 100
S = 1002 = 10 000 cm2
It turns out that there are ten thousand square centimeters per square meter.
1 m2 = 10 000 cm2
This allows you to multiply any number of square meters by 10,000 in the future and get the area expressed in square centimeters.
To convert square meters into square centimeters, multiply the number of square meters by 10 000.
And to convert square centimeters into square meters, it is necessary to divide the number of square centimeters by 10 000.
For example, let's convert 100 000 cm2 into square meters. The reasoning in this case can be: "if 10,000 cm2 is one square meter, how many times 100,000 cm2 will contain 10,000 cm2"
100 000 cm2 : 10 000 cm2 = 10 m2
Other units can be converted in the same way. For example, let's convert 2 km2 to square meters.
One square kilometer is a square with a side of 1 kilometer. That is, all four sides have a length equal to one kilometer. But 1 km = 1000 m. So all four sides of the square are also 1000 meters. Find the new area of the square expressed in square meters. To do this, multiply the length of 1000 m by the width of 1000 m or square the number 1000
S = 10002 = 1 000 000 m2
It turns out that there are one million square meters per square kilometer:
1 km2 = 1 000 000 m2
This allows you to multiply any number of square kilometers by 1,000,000 in the future and get the area expressed in square meters.
To convert square kilometers into square meters, multiply the number of square kilometers by 1 000 000.
So let's go back to our task. We needed to convert 2 km2 into square meters. Let's multiply 2 km2 by 1 000 000
2 km2 × 1 000 000 = 2 000 000 m2
And to convert square meters into square kilometers, it is necessary to divide the number of square meters by 1 000 000.
For example, let's convert 3 500 000 m2 to square kilometers. The reasoning in this case could be, "If 1 000 000 m2 is one square kilometer, how many times will 3 500 000 m2 contain 1 000 000 m2"
3 500 000 m2 : 1 000 000 m2 = 3.5 km2
Example 2. Express 7 m2 in square centimeters.
Let's multiply 7 m2 by 10 000
7 m2 = 7 m2 × 10 000 = 70 000 cm2
Example 3. Express 5 m2 13 cm2 in square centimeters.
5 m2 13 cm2 = 5 m2 × 10 000 + 13 cm2 = 50 013 cm2
Example 4. Express 550,000 cm2 in square meters.
Let's find out how many times 550,000 cm2 contains 10,000 cm2. To do this, divide 550,000 cm2 by 10,000 cm2
550 000 cm2 : 10 000 cm2 = 55 m2
Example 5. Express 7 km2 in square meters.
Multiply 7 km2 by 1 000 000
7 km2 × 1 000 000 = 7 000 000 m2
Example 6. Express 8,500,000 m2 in square kilometers.
Let's find out how many times 8 500 000 m2 contains 1 000 000 m2. To do this, divide 8 500 000 m2 by 1 000 000 m2
8 500 000 m2 × 1 000 000 m2 = 8.5 km2
Units of measurement of the area of land plots
The area of small plots of land is conveniently measured in square meters.
The areas of larger land plots are measured in acres and hectares.
Ar (abbreviated: a) is an area equal to one hundred square meters (100 m2). In view of the frequent spread of such an area (100 m2), it came to be used as a separate unit of measurement.
For example, if it says that the area of some field is 3 a, then you need to understand that this is three squares of 100 m2 each, that is:
3 a = 100 m2 × 3 = 300 m2
The acre is a unit of land area used in the imperial and US customary systems. It is traditionally defined as the area of one chain by one furlong (66 by 660 feet), which is exactly equal to 10 square chains, 1⁄640 of a square mile, or 43,560 square feet, and approximately 4,047 m2, or about 40% of a hectare. Based upon the International yard and pound agreement of 1959, an acre may be declared as exactly 4,046.8564224 square metres. The acre was sometimes abbreviated ac, but was often spelled out as the word "acre".
A hectare (abbreviated: ha) is an area equal to 10 000 m2. For example, if it is said that the area of some forest is 20 hectares, it must be understood that these are twenty squares of 10 000 m2 each, that is:
20 ha = 10 000 m2 × 20 = 200 000 m2
Rectangular parallelepiped and cube
A rectangular parallelepiped is a geometric figure consisting of faces, edges and vertices. The figure shows a rectangular parallelepiped:
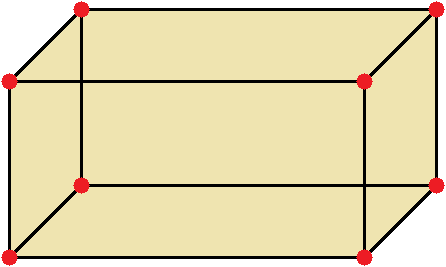
Yellow color shows the faces of the parallelepiped, black color - the edges, red - the vertices.
A rectangular parallelepiped has length, width and height. The figure shows where the length, width, and height are:

A parallelepiped whose length, width, and height are equal to each other is called a cube. The figure shows a cube:

The volume of a geometric figure
The volume of a geometric figure is a number that characterizes the capacity of that figure.
Volume is measured in cubic units. Cubic units refer to cubes of length 1, width 1, and height 1. For example, 1 cubic centimeter or 1 cubic meter.
To measure the volume of any shape means to find out how many cubic units fit into that shape.
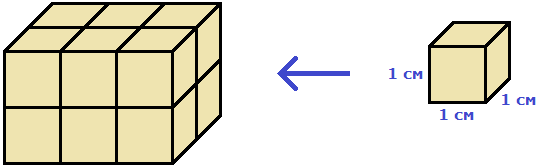
For example, the volume of the following rectangular parallelepiped is twelve cubic centimeters:
This is because this parallelepiped fits twelve cubes 1 cm long, 1 cm wide and 1 cm high:
Volume is denoted by the capital Latin letter V. One of the units of volume measurement is cubic centimeter (cm3). Then the volume V of our considered parallelepiped is 12 cm3
V = 12 cm3
The volume of any parallelepiped is calculated as follows: multiply its length, width and height.
The volume of a rectangular parallelepiped is equal to the product of its length, width and height.
V = abc
where, a - length, b - width, c - height
So, in the previous example, we visually determined that the volume of the parallelepiped is 12 cm3. But we can measure the length, width and height of this parallelepiped and multiply the results of measurements. We will get the same result

The volume of a cube is calculated in the same way as the volume of a rectangular parallelepiped - multiply the length, width and height.
For example, let's calculate the volume of a cube whose length is 3 cm. A cube has length, width, and height equal to each other. If length is equal to 3 cm, then width and height of the cube are equal to the same three centimeters:
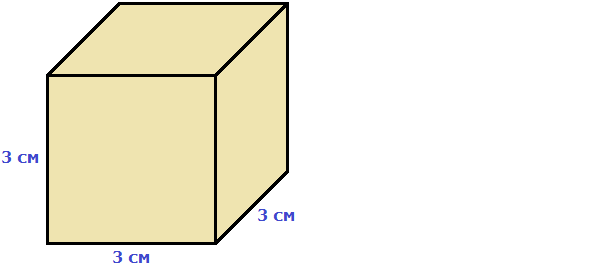
Multiply the length, width, height and we get a volume equal to twenty-seven cubic centimeters:
V = 3 × 3 × 3 = 27 cm3
Indeed, the original cube holds 27 cubes of length 1 cm
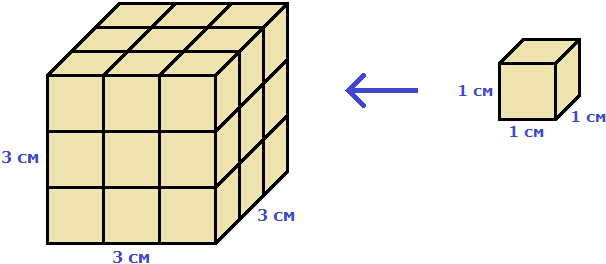
To calculate the volume of this cube, we multiplied the length, width, and height. The product is 3 × 3 × 3. This is the product of three factors each equal to 3. That is, the product 3 × 3 × 3 is the third power of 3 and can be written as 33.
V = 33 = 27 cm3
Therefore, the third power of a number is called the cube of a number. When calculating the third power of a number a, one finds the volume of a cube of length a. The operation of exponentiation of a number to the third power is otherwise called cube exponentiation.
Thus, the volume of the cube is calculated by the following rule:
V = a3
Where a is the length of the cube.
Cubic decimeter. Cubic meter
Not all objects in our world are conveniently measured in cubic centimeters. For example, it is more convenient to measure the volume of a room or a house in cubic meters (m3). And it is more convenient to measure the volume of a tank, aquarium or refrigerator in cubic decimeters (dm3).
Another name for one cubic decimeter is one liter.
1 dm3 = 1 liter
Conversion of volume units
Volume units can be converted from one unit of measure to another. Let's look at a few examples:
Example 1. Express 1 cubic meter in cubic centimeters.
One cubic meter is a cube with a side of 1 meter. The length, width, and height of this cube are equal to one meter.
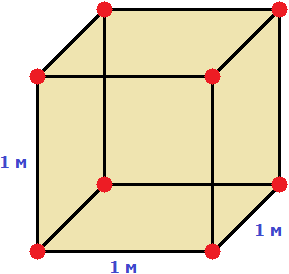
But 1 m = 100 cm. So the length, width, and height are also 100 cm.

Let's calculate the new volume of the cube, expressed in cubic centimeters. To do this, multiply its length, width and height. Or let's multiply the number 100 by the cube:
V = 1003 = 1 000 000 cm3
It turns out that there are one million cubic centimeters per cubic meter:
1 m3 = 1 000 000 cm3
This allows you to multiply any number of cubic meters by 1 000 000 in the future to get the volume expressed in cubic centimeters.
To convert cubic meters into cubic centimeters, multiply the number of cubic meters by 1 000 000.
And to convert cubic centimeters into cubic meters, it is necessary to divide the number of cubic centimeters by 1 000 000.
For example, let's convert 300,000,000,000 cm3 to cubic meters. The reasoning in this case could be, "if 1,000,000 cm3 is one cubic meter, how many times will 300,000,000 cm3 contain 1,000,000 cm3?"
300 000 000 cm3 : 1 000 000 cm3 = 300 m3
Example 2. Express 3 m3 in cubic centimeters.
Multiply 3 m3 by 1 000 000
3 m3 × 1 000 000 = 3 000 000 cm3
Example 3. Express 60,000,000 cm3 in cubic meters.
Let's find out how many times 60 000 000 cm3 contains 1 000 000 cm3. To do this, divide 60 000 000 cm3 by 1 000 000 cm3
60 000 000 cm3 : 1 000 000 cm3 = 60 m3
The capacity of a tank, can or jerry can is measured in liters. A liter is also a unit of volume measurement. One liter is equal to one cubic decimeter.
1 liter = 1 dm3
For example, if the capacity of a jar is 1 liter, it means that the volume of this jar is 1 dm3. When solving some tasks, it can be useful to know how to convert liters to cubic decimeters and vice versa. Let's look at some examples.
Example 1. To convert 5 liters to cubic decimeters.
To convert 5 liters to cubic decimeters, simply multiply 5 by 1
5 l × 1 = 5 dm3
Example 2. Translate 6 000 liters into cubic meters.
Six thousand liters is six thousand cubic decimeters:
6000 l × 1 = 6000 dm3
Now let's convert these 6000 dm3 into cubic meters.
The length, width, and height of one cubic meter are 10 dm
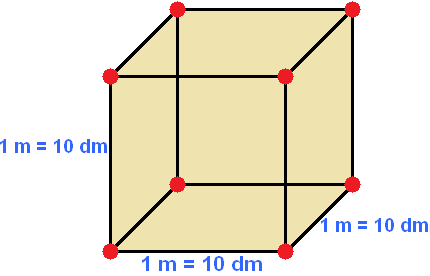
If we calculate the volume of this cube in decimeters, we get 1000 dm3
V = 103= 1000 dm3
It turns out that one thousand cubic decimeters corresponds to one cubic meter. And to determine how many cubic meters correspond to six thousand cubic decimeters, we need to know how many times 6 000 dm3 contains 1 000 dm3
6 000 dm3 : 1 000 dm3 = 6 m3
So 6000 l = 6 m3.
Table of squares
In life we often have to find the areas of different squares. To do this each time it is necessary to raise the original number to the second power.
The squares of the first 99 natural numbers have already been calculated and entered into a special table called the table of squares.
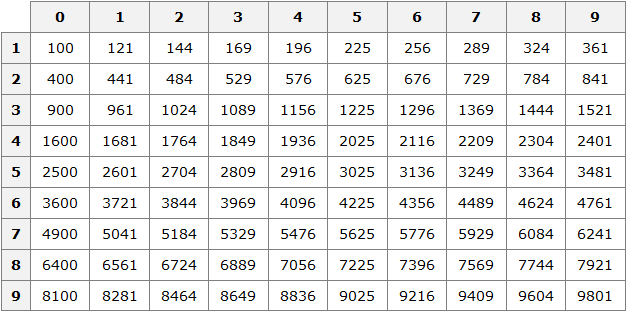
The first row of this table (digits from 0 to 9) are units of the original number, and the first column (digits from 1 to 9) are tens of the original number.
For example, find the square of number 24 using this table. The number 24 consists of the digits 2 and 4. More precisely, the number 24 consists of two tens and four ones.
So, choose number 2 in the first column of the table (the column of tens), and choose number 4 in the first row (the row of units). Then move to the right of digit 2 and down from digit 4 to find the intersection point. As a result, we will find the position where the number 576 is located. This means that the square of 24 is 576.
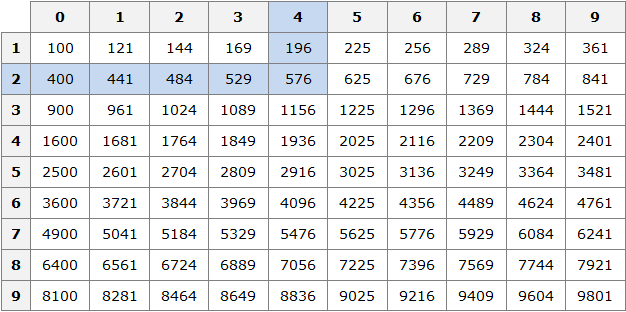
242 = 576
Table of cubes
As in the situation with squares, the cubes of the first 99 natural numbers have already been calculated and entered into a table called the table of cubes.
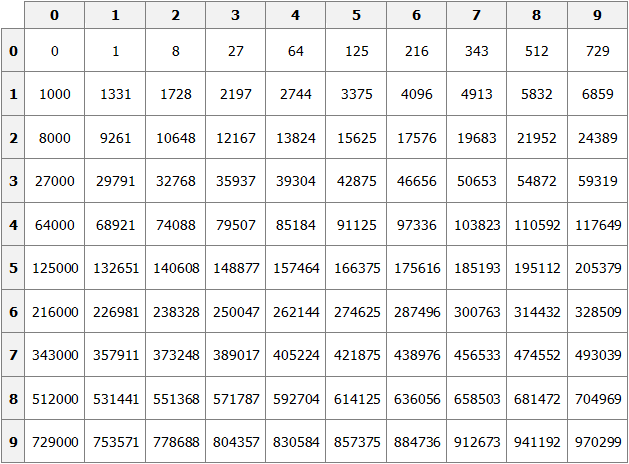
The cube of a number is defined in the same way as the square of a number. For example, find the cube of the number 35. This number consists of digits 3 and 5. Select digit 3 in the first column of the table (the column of tens), and digit 5 in the first row (the row of units). Move to the right of digit 3 and down from digit 5 to find the intersection point. As a result, we find ourselves at the position where the number 42875 is located. So the cube of 35 is 42875.
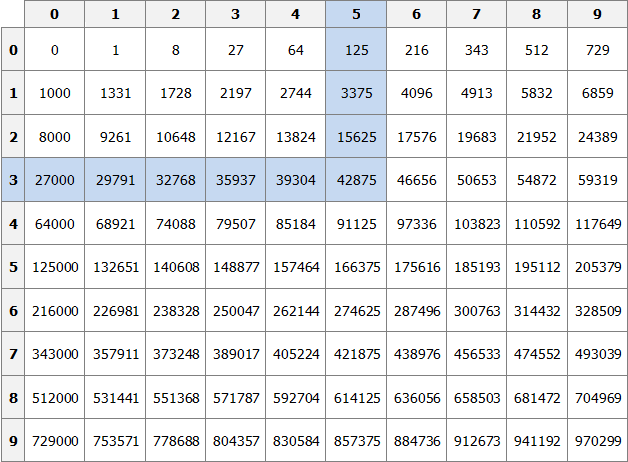
353 = 42875
Tasks for independent decision
Solution
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 cm
Answer: the perimeter of the rectangle is 16 cm.
Solution
S = ab
a = 6, b = 2
S = 6 × 2 = 12 cm2
Answer: the area is 12 cm2.
Solution
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Answer: the width of the rectangle is 2 cm.
Solution
S = a2
a = 8
S = 82 = 64 cm2
Answer: the area of a square with a side of 8 cm is 642
Solution
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 cm3.
Answer: the volume of a rectangular parallelepiped with length 6 cm, width 4 cm, height 3 cm is 72 cm3
Solution
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Answer: the height of the rectangular parallelepiped is 4 cm.
Solution
The number 4 represents the area sown with wheat. The number 5 represents the area sown with flax.
The areas sown with wheat and flax are said to be proportional to these numbers.
Simply put, by how many times the numbers 4 or 5 change, by how many times the area that is sown with wheat or flax will also change. Fifteen hectares are sown with flax. That is, the number 5, which reflects the area sown with flax, has changed by a factor of 3.
Then the number 4, which reflects the area sown with wheat, should be tripled.
4 × 3 = 12 ha
Answer: 12 hectares were sown with wheat.
Solution
a - length
b - width
c - height
a = 42 m
b = ![]() m
m
c = 42 × 0.1 = 4.2m
Let's define the volume of the granary:
V = abc = 42 × 30 × 4.2 = 5292 m3
Determine how many tons of grain the granary can hold:
5292 × 740 = 3916080 kg
Let's convert kilograms to tons:
![]()
Answer: The granary holds 3916.08 tons of grain.
Solution
Determine how many liters per minute flow through the second tube:
25 l/min × 0.75 = 18.75 l/min.
Determine how many liters per minute are flowing into the pool through both pipes:
25 l/min + 18.75 l/min = 43.75 l/min.
Let's find out how many liters of water will be poured into the pool in 13 h 32 min.
43.75 × 13 h 32 min = 43.75 × 812 min = 35,525 l
1 l = 1 dm3
35 525 l = 35 525 dm3
Let's convert cubic decimeters to cubic meters. This will allow you to calculate the volume of the pool:
35 525 dm3 : 1000 dm3 = 35 525 m3
Knowing the volume of the pool, you can calculate the height of the pool. Let's substitute the values we have in the letter equation V=abc. Then we get:
V = 35,525
a = 5.8
b = 3.5
c = x
35 525 = 5.8 × 3.5 × x
35 525 = 20.3 × x
x = 1.75 m
с = 1.75
Answer: the height (depth) of the pool is 1.75 m.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.