This material may seem difficult to understand. It is recommended that you study it in small portions.
Definitions and properties
We will call two numeric or alphabetic expressions connected by signs >, <, ≥, ≤ or ≠ an inequality.
Example: 5 > 3
This inequality says that the number 5 is greater than the number 3. The acute angle of the inequality sign must point toward the smaller number. This inequality is true because 5 is greater than 3.
If you put a watermelon weighing 5 kg on the left-hand scale and a watermelon weighing 3 kg on the right-hand scale, the left-hand scale will outweigh the right-hand scale and the scale screen will show that the left-hand scale is heavier than the right-hand scale:
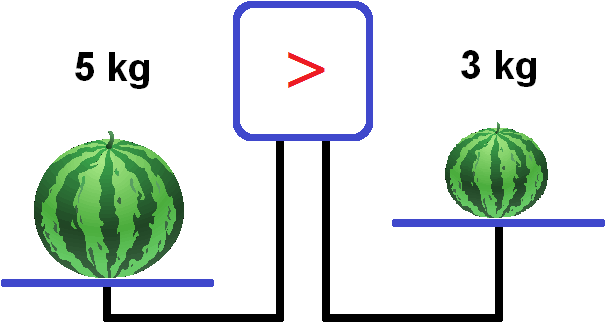
If 5 > 3, then 3 < 5. That is, the left and right parts of the inequality can be swapped by changing the sign of the inequality to the opposite. In the scales situation: a large watermelon can be placed on the right bowl and a small watermelon on the left bowl. Then the right bowl will outweigh the left bowl and the screen will show the sign <
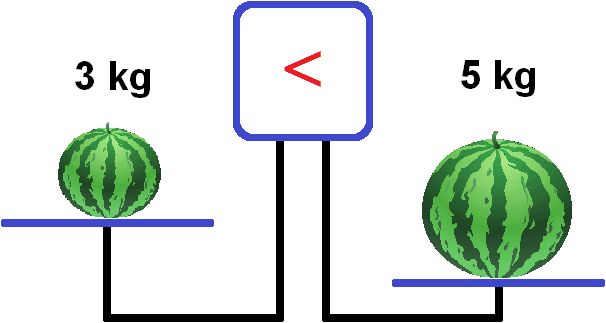
If you change the sign of the inequality 5 > 3 without touching the left and right parts to <, you get the inequality 5 < 3. This inequality is not true because number 3 cannot be greater than number 5.
The numbers on the left and right sides of the inequality are called members of the inequality. For example, in the inequality 5 > 3, the members are numbers 5 and 3.
Consider some important properties for the inequality 5 > 3.
In the future, these properties will work for other inequalities as well.
Property 1.
If you add or subtract the same number to the left and right sides of an inequality 5 > 3, the sign of the inequality will not change.
For example, add the number 4 to both parts of the inequality:
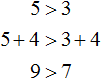
We see that the left side is still larger than the right.
Now let's try to subtract from both parts of the inequality 5 > 3 some number, say number 2
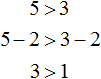
We see that the left side is still larger than the right.
It follows from this property that any term of an inequality can be transferred from one part to another part by changing the sign of that term. The sign of the inequality will not change.
For example, in the inequality 5 > 3, move the term 5 from the left side to the right side by changing the sign of the term. After moving the term 5 to the right side, there will be nothing left in the left side, so we write there 0
0 > 3 − 5
0 > −2
We see that the left side is still larger than the right.
Property 2.
If both parts of an inequality are multiplied or divided by the same positive number, the sign of the inequality will not change.
For example, multiply both parts of the inequality 5 > 3 by some positive number, say number 2. Then we get:
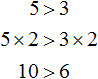
We see that the left side is still larger than the right.
Now let's try to divide both parts of the inequality 5 > 3 by some number. Let's divide them by 2
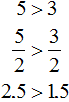
We see that the left side is still larger than the right.
Property 3.
If both parts of an inequality are multiplied or divided by the same negative number, then the sign of the inequality is reversed.
For example, multiply both parts of the inequality 5 > 3 by some negative number, say -2. Then we get:
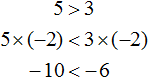
We see that the left side is less than the right. That is, the sign of the inequality is reversed.
Now let's try to divide both parts of the inequality 5 > 3 by some negative number. Let's divide them by -1
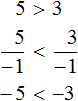
We see that the left side is less than the right. That is, the sign of the inequality is reversed.
The inequality itself can be understood as a condition. If the condition is satisfied, the inequality is true. And vice versa, if the condition is not satisfied, the inequality is not true.
For example, to answer the question whether the inequality 7 > 3 is true, we need to check whether the condition "whether 7 is greater than 3" is true. We know that the number 7 is greater than the number 3. That is, the condition is satisfied, so the inequality 7 > 3 is true.
The inequality 8 < 6 is not true because the condition "8 is less than 6" is not satisfied.
Another way to determine if an inequality is true is to make up the difference between the left and the right side of the given inequality. If the difference is positive, then the left side is greater than the right side. Conversely, if the difference is negative, then the left side is smaller than the right side. More precisely, this rule looks like this:
The number a is greater than the number b if the difference a - b is positive. The number a is less than the number b if the difference a - b is negative.
For example, we found out that the inequality 7 > 3 is true because the number 7 is greater than the number 3. Let's prove it using the rule above.
Make the difference between the terms 7 and 3. Then we get 7 - 3 = 4. According to the rule, the number 7 is greater than 3 if the difference 7 - 3 is positive. We have it equal to 4, so the difference is positive. So the number 7 is greater than the number 3.
Use the difference to check if the inequality 3 < 4 is true. Make up the difference, we get 3 - 4 = -1. According to the rule, number 3 is less than number 4 if the difference 3 - 4 is negative. We have it equal to -1, so the difference is negative. So the number 3 is less than the number 4.
Let's check if the inequality 5 > 8 is true. Make up the difference, we get 5 - 8 = -3. According to the rule, number 5 is greater than number 8 if the difference 5 - 8 is positive. Our difference is -3, so it is not positive. So the number 5 is not greater than the number 3. In other words, the inequality 5 > 8 is not true.
Strict and non-strict inequalities
Inequalities containing signs >, < are called strict. Inequalities with signs ≥, ≤ are called non-strict.
Examples of strict inequalities we looked at earlier. These are inequalities 5 > 3, 7 < 9.
For example, the inequality 2 ≤ 5 is not strict. This inequality reads as follows: "2 is less than or equal to 5."
The entry 2 ≤ 5 is incomplete. The complete writing of this inequality is as follows:
2 < 5 or 2 = 5
Then it becomes obvious that the inequality 2 ≤ 5 consists of two conditions: "two less than five" and "two equals five".
A non-strict inequality is true if at least one of its conditions is satisfied. In our example, the condition "2 is less than 5" is true. So the inequality 2 ≤ 5 is also true.
Example 2. The inequality 2 ≤ 2 is true because one of its conditions is satisfied, namely 2 = 2.
Example 3. The inequality 5 ≤ 2 is not true because none of its conditions is satisfied: neither 5 < 2 nor 5 = 2.
Double Inequality
The number 3 is greater than the number 2 and less than the number 4. We can write it as an inequality: 2 < 3 < 4. Such an inequality is called a double inequality.
Double inequalities can contain signs of non-strict inequalities. For example, if the number 5 is greater than or equal to the number 2, and less than or equal to the number 7, then we can write that 2 ≤ 5 ≤ 7
To correctly write a double inequality, first write the term in the middle, then the term on the left, then the term on the right.
For example, write down that number 6 is greater than number 4, and less than number 9.
First we write down 6
![]()
On the left, write down that this number is greater than the number 4
![]()
On the right, write down that the number 6 is less than the number 9
![]()
Inequality with a variable
An inequality, like an equality, can contain a variable.
For example, an inequality x > 2 contains the variable x. Usually such an inequality needs to be solved, that is, to find out at what values of x this inequality becomes true.
To solve an inequality means to find such values of the variable x at which the given inequality becomes true.
The value of the variable at which the inequality becomes true is called the solution to the inequality.
The inequality x > 2 becomes true at x = 3, x = 4, x = 5, x = 6, and so on to infinity. We see that this inequality has not just one solution, but many solutions.
In other words, the solution of x > 2 is the set of all numbers greater than 2. At these numbers, the inequality will be true. Examples:
3 > 2
4 > 2
5 > 2
The number 2 on the right side of the inequality x > 2 will be called the boundary of the inequality. Depending on the sign of the inequality, the boundary may or may not belong to the solution set of the inequality.
In our example, the boundary of the inequality does not belong to the set of solutions because substituting the number 2 into the inequality x > 2 does not result in the correct inequality 2 > 2. The number 2 cannot be greater than itself because it is equal to itself (2 = 2).
The inequality x > 2 is strict. It can be read as "x is strictly greater than 2″. That is, all values taken by the variable x must be strictly greater than 2. Otherwise, the inequality will not be true.
If we were given a non-strict inequality x ≥ 2, then the solutions to this inequality would be all numbers that are greater than 2, including the number 2 itself. In this inequality, the boundary 2 belongs to the set of solutions to the inequality because substituting the number 2 into the inequality x ≥ 2 results in the correct inequality 2 ≥ 2. It was said earlier that a non-strict inequality is true if at least one of its conditions is satisfied. In the inequality 2 ≥ 2, the condition 2 = 2 is satisfied, so the inequality 2 ≥ 2 itself is true.
How to solve inequalities
The process of solving inequalities is much the same as solving equations. When solving inequalities, we will apply the properties we learned at the beginning of this lesson, such as: transferring the summands from one part of an inequality to another part, changing the sign; multiplying (or dividing) both parts of an inequality by the same number.
These properties allow us to obtain an inequality that is equivalent to the original inequality. Equivalent inequalities are inequalities whose solutions coincide.
Solving equations we performed identity transformations until there was no variable on the left side of the equation, and the value of that variable remained on the right side (for example: x = 2, x = 5). That is, replace the original equation with an equivalent equation until you have an equation of the form x = a, where a is the value of the variable x. Depending on the equation, there could be one, two, an infinite number, or no roots at all.
And when solving inequalities, we will replace the original inequality with an equivalent inequality until there is no variable of that inequality on the left side, and its boundary on the right side.
Example 1. Solve an inequality 2x > 6
So, we need to find values of x which, when substituted into 2x > 6, will result in a correct inequality.
It was said at the beginning of this lesson that if both parts of an inequality are divided by some positive number, the sign of the inequality will not change. If we apply this property to an inequality that contains a variable, we get an inequality equal to the original inequality.
In our case, if we divide both parts of the inequality 2x > 6 by some positive number, we will get an inequality that is equivalent to the original inequality 2x > 6.
So, divide both parts of the inequality by 2.
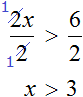
The variable x remains on the left side, and the right side equals 3. We obtained an equal inequality x > 3. This completes the solution, because the left part contains the variable and the right part contains the boundary of the inequality.
Now we can conclude that the solutions of the inequality x > 3 are all numbers that are greater than 3. These are numbers 4, 5, 6, 7, and so on to infinity. At these values, the inequality x > 3 will be true.
4 > 3
5 > 3
6 > 3
7 > 3
Note that the inequality x > 3 is strict. "The variable x is strictly greater than three".
And since the inequality x > 3 is equivalent to the original inequality 2x > 6, their solutions will coincide. In other words, values that fit the x > 3 inequality will also fit the 2x > 6 inequality. Let's show this.
For example, take number 5 and substitute it first into the equational inequality x > 3 and then into the original 2x > 6.
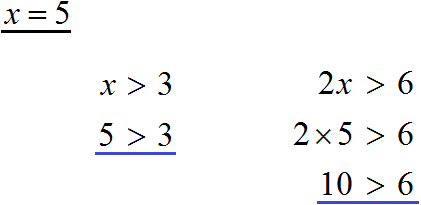
We see that in both cases the inequality is correct.
After the inequality is solved, the answer must be written in the form of a so-called numerical interval as follows:
![]()
This expression says that the values taken by the variable x belong to the numerical interval from three to plus infinity.
In other words, all numbers from three to plus infinity are solutions to the inequality x > 3. The sign ∞ in mathematics means infinity.
Given that the concept of a numerical interval is very important, let's dwell on it in more detail.
Numerical intervals
A number interval is a set of numbers on a coordinate line that can be described by an inequality.
Suppose we want to represent the set of numbers from 2 to 8 on a coordinate line. To do this, first on a coordinate line marked points with coordinates 2 and 8, and then highlight the strokes that are located between the coordinates 2 and 8. Imagine that the strokes are numbers located between the numbers 2 and 8.

Numbers 2 and 8 are called the boundaries of the numerical interval. When drawing a numerical interval, the points for its boundaries are depicted not as points as such, but as circles, which can be seen.
The boundaries may or may not belong to the numeric interval.
If the boundaries do not belong to the numerical interval, they are represented on the coordinate line as empty circles.
If the boundaries belong to the numeric interval, the circles must be painted over.
In our figure, the circles were left empty. This meant that the borders of 2 and 8 do not belong to the numerical space. So our numerical interval will include all numbers from 2 to 8, except for the numbers 2 and 8.
If we want to include the borders of 2 and 8 in the numerical interval, the circles must be painted over:
![]()
In this case, the numeric interval will include all numbers from 2 to 8, including the numbers 2 and 8.
In writing, the numeric interval is indicated by indicating its boundaries with round or square brackets.
If the boundaries do not belong to a numeric interval, the boundaries are surrounded by round brackets.
If the boundaries belong to a numeric range, the boundaries are surrounded by square brackets.
The figure shows two numeric intervals from 2 to 8 with corresponding symbols:
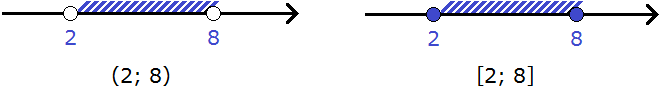
In the first figure the numeric interval is denoted by round brackets, because the borders of 2 and 8 do not belong to this numeric interval.
In the second figure the numeric interval is marked with square brackets, because the borders of 2 and 8 belong to this numeric interval.
You can use number spaces to write answers to inequalities. For example, the answer to a double inequality 2 ≤ x ≤ 8 is written as follows:
x ∈ [ 2 ; 8 ]
That is, we first write down the variable that is part of the inequality, and then use an identity symbol ∈ to indicate which numerical interval the values of that variable belong to. In this case, the expression x ∈ [ 2 ; 8 ] indicates that the variable x in the inequality 2 ≤ x ≤ 8 takes all values between 2 and 8. At these values the inequality will be true.
Note that the answer is written using square brackets because the boundaries of the inequality 2 ≤ x ≤ 8, namely, the numbers 2 and 8 belong to the set of solutions to this inequality.
The set of solutions to the inequality 2 ≤ x ≤ 8 can also be represented using the coordinate line:
![]()
Here, the boundaries of the numerical interval 2 and 8 correspond to the boundaries of the inequality 2 ≤ x ≤ 8, and the highlighted area corresponds to the set of values of x, which are solutions of the inequality 2 ≤ x ≤ 8.
In some sources, boundaries that do not belong to a numerical interval are called open boundaries.
They are called open for the reason that a numerical interval remains open because its boundaries do not belong to this numerical interval. An empty circle on the coordinate line is called a pricked point. To prick a point means to exclude it from the numerical interval or from the set of solutions to an inequality.
In the case when the boundaries belong to the numeric interval, they are called closed, because such boundaries close the numeric interval. A shaded circle on the coordinate line also indicates that the boundaries are closed.
There are varieties of numerical intervals. Let us consider each of them.
Numeric Ray
A number ray is a number interval defined by the inequality x ≥ a, where a is the boundary of the given inequality, x is the solution of the inequality.
Let a = 3. Then the inequality x ≥ a will look like x ≥ 3. The solutions of this inequality are all numbers that are greater than 3, including the number 3 itself.
Let us represent the number ray given by the inequality x ≥ 3 on the coordinate line. To do this, mark the point with coordinate 3 on it, and mark all the remaining area to its right with strokes. The right part is selected because the solutions of the inequality x ≥ 3 are numbers greater than 3. And the larger numbers on the coordinate line are located to the right
![]()
Here, point 3 corresponds to the boundary of the inequality x ≥ 3, and the area highlighted with strokes corresponds to the set of values of x that are solutions of the inequality x ≥ 3.
Point 3, which is the boundary of the number ray, is shown as a shaded circle because the boundary of the inequality x ≥ 3 belongs to the set of its solutions.
In writing, a number ray given by the inequality x ≥ a is denoted as follows:
[ a ; +∞ )
You can see that one side of the boundary is framed by a square bracket and the other by a round bracket. This is due to the fact that one boundary of the number ray belongs to it, and the other does not, because infinity itself has no boundaries, and it is implied that on the other side there is no number closing the number ray.
Given that one of the borders of the number ray is closed, this gap is often called a closed number ray.
Let us write the answer to the inequality x ≥ 3 using the number ray notation. We have the variable a equal to 3
x ∈ [ 3 ; +∞ )
This expression says that the variable x included in the inequality x ≥ 3 takes all values from 3 to plus infinity.
Or you could put it another way, all numbers from 3 to plus infinity are solutions to the inequality x ≥ 3. The boundary 3 belongs to the set of solutions because the inequality x ≥ 3 is non-strict.
A closed number ray is also called a number interval, which is given by the inequality x ≤ a. Solutions of the inequality x ≤ a are all numbers that are less than a, including the number a itself.
For example, if a = 2, the inequality will look like x ≤ 2. On the coordinate line, the boundary 2 will be shown as a shaded circle, and the whole area to the left will be highlighted with strokes. This time the left part is highlighted, because the solutions of the inequality x ≤ 2 are numbers smaller than 2. And the smaller numbers on the coordinate line are on the left
![]()
Here point 2 corresponds to the boundary of the inequality x ≤ 2, and the shaded area corresponds to the set of values of x which are solutions of the inequality x ≤ 2.
Point 2, which is the boundary of the number ray, is shown as a shaded circle, because the boundary of the inequality x ≤ 2 belongs to the set of its solutions.
Write the answer to the inequality x ≤ 2 using the notation of the number ray:
x ∈ ( −∞ ; 2 ]
This expression says that all numbers from minus infinity to 2, are solutions to the inequality x ≤ 2. The boundary 2 belongs to the set of solutions, because the inequality x ≤ 2 is non-strict.
Open number ray
An open number ray is a number interval defined by the inequality x > a, where a is the boundary of the given inequality, x is the solution to the inequality.
An open number ray is much like a closed number ray. The difference is that the boundary a does not belong to the interval, just as the boundary of the inequality x > a does not belong to the set of its solutions.
Let a = 3. Then the inequality will look like x > 3. The solutions of this inequality are all numbers greater than 3, except for the number 3
On the coordinate line the boundary of the open number ray given by the inequality x > 3 will be shown as an empty circle. The entire area to the right will be highlighted with strokes:
![]()
Here point 3 corresponds to the boundary of the inequality x > 3, and the highlighted area corresponds to the set of values of x which are solutions of the inequality x > 3. Point 3, which is the boundary of the open number ray, is shown as an empty circle, because the boundary of the inequality x > 3 does not belong to the set of its solutions.
In writing, the open number ray given by the inequality x > a is denoted as follows:
( a ; +∞ )
The parentheses indicate that the boundaries of the open number ray do not belong to it.
Let us write the answer to the inequality x > 3 using the notation of an open number ray:
x ∈ ( 3 ; +∞ )
This expression says that all numbers from 3 to plus infinity, are solutions to the inequality x > 3. The boundary 3 does not belong to the set of solutions, because the inequality x > 3 is strict.
An open number ray is also a number interval, which is given by the inequality x < a, where a is the boundary of the given inequality, x is the solution to the inequality. Solutions to the inequality x < a are all numbers that are less than a, excluding the number a.
For example, if a = 2, the inequality will look like x < 2. On the coordinate line, the boundary 2 will be shown as an empty circle, and all the area to the left will be highlighted with strokes:
![]()
Here point 2 corresponds to the boundary of the inequality x < 2, and the highlighted area corresponds to the set of values of x which are solutions of the inequality x < 2. Point 2, which is the boundary of the open number ray, is shown as an empty circle, because the boundary of the inequality x < 2 does not belong to the set of its solutions.
In writing, the open number ray given by the inequality x < a is denoted as follows:
( −∞ ; a )
Let us write the answer to the inequality x < 2 using the notation of an open number ray:
x ∈ ( −∞ ; 2 )
This expression says that all numbers from minus infinity to 2, are solutions to the inequality x < 2. The boundary 2 does not belong to the set of solutions, because the inequality x < 2 is strict.
Segment
A segment is a numerical interval that is given by the double inequality a ≤ x ≤ b, where a and b are the boundaries of the given inequality, x is the solution of the inequality.
Let a = 2, b = 8. Then the inequality a ≤ x ≤ b becomes 2 ≤ x ≤ 8. Solutions of the inequality 2 ≤ x ≤ 8 are all numbers greater than 2 and smaller than 8. The boundaries of the inequality 2 and 8 belong to the set of its solutions, because the inequality 2 ≤ x ≤ 8 is non-strict.
Let us represent the segment given by the dual inequality 2 ≤ x ≤ 8 on the coordinate line. To do this, mark points with coordinates 2 and 8 on the coordinate line, and mark the area between them with strokes:

Here points 2 and 8 correspond to the boundaries of the inequality 2 ≤ x ≤ 8, and the shaded area corresponds to the set of values of x, which are solutions of the inequality 2 ≤ x ≤ 8. The points 2 and 8, which are the borders of the segment, are shown as shaded circles, because the borders of the inequality 2 ≤ x ≤ 8 belong to the set of its solutions.
On the letter, the segment given by the inequality a ≤ x ≤ b is denoted as follows:
[ a ; b ]
The square brackets on both sides indicate that the borders of the segment belong to it. Let us write the answer to the inequality 2 ≤ x ≤ 8 using this notation:
x ∈ [ 2 ; 8 ]
This expression says that all numbers from 2 to 8, inclusive, are solutions to the inequality 2 ≤ x ≤ 8.
Interval
An interval is a numerical interval given by a double inequality a < x < b, where a and b are the limits of the given inequality, x is the solution of the inequality.
Let a = 2, b = 8. Then the inequality a < x < b will take the form 2 < x < 8. The solutions of this double inequality are all numbers that are greater than 2 and less than 8, excluding the numbers 2 and 8.
Let us represent the interval on the coordinate line:

Here points 2 and 8 correspond to the bounds of the inequality 2 < x < 8, and the hatched area corresponds to the set of values of x which are solutions of the inequality 2 < x < 8. The points 2 and 8, which are the borders of the interval, are shown as empty circles, because the borders of the inequality 2 < x < 8 do not belong to the set of its solutions.
In writing, the interval given by the inequality a < x < b is denoted as follows:
( a ; b )
The round brackets on both sides indicate that the boundaries of the interval do not belong to it. Let us write the answer to the inequality 2 < x < 8 using this notation:
x ∈ ( 2 ; 8 )
This expression says that all numbers from 2 to 8, excluding numbers 2 and 8, are solutions to the inequality 2 < x < 8.
Half-interval
A half-interval is a numerical interval that is given by the inequality a ≤ x < b, where a and b are the limits of the given inequality, x is the solution of the inequality.
A half-interval is also a numerical interval, which is defined by the inequality a < x ≤ b.
One of the boundaries of the half-interval belongs to it. Hence the name of this numerical interval.
In the situation with the half-interval a ≤ x < b it (the half-interval) belongs to the left boundary.
And in the situation with the half-interval a < x ≤ b it belongs to the right boundary.
Let a = 2, b = 8. Then the inequality a ≤ x < b will take the form 2 ≤ x < 8. Solutions of this dual inequality are all numbers that are greater than 2 and less than 8, including the number 2, but excluding the number 8.
Let's represent the half-interval 2 ≤ x < 8 on the coordinate line:

Here points 2 and 8 correspond to the boundaries of the inequality 2 ≤ x < 8, and the highlighted area corresponds to the set of values of x, which are solutions of the inequality 2 ≤ x < 8.
Point 2, which is the left boundary of the half-interval, is shown as a shaded circle, because the left boundary of the inequality 2 ≤ x < 8 belongs to the set of its solutions.
The point 8, which is the right boundary of the half-interval, is shown as an empty circle because the right boundary of the inequality 2 ≤ x < 8 does not belong to the set of its solutions.
In writing, the half-interval given by the inequality a ≤ x < b is denoted as follows:
[ a ; b )
You can see that one side of the boundary is framed by a square bracket and the other by a round bracket. This is due to the fact that one boundary of the half-interval belongs to it, and the other does not. Write down the answer to the inequality 2 ≤ x < 8 using this notation:
x ∈ [ 2 ; 8 )
This expression says that all numbers from 2 to 8, including number 2 but excluding number 8, are solutions to the inequality 2 ≤ x < 8.
Similarly, on a coordinate line we can represent a half-interval given by the inequality a < x ≤ b. Let a = 2, b = 8. Then the inequality a < x ≤ b will take the form 2 < x ≤ 8. Solutions to this dual inequality are all numbers that are greater than 2 and less than 8, excluding the number 2 but including the number 8.
Let's represent the half-interval 2 < x ≤ 8 on the coordinate line:

Here points 2 and 8 correspond to the boundaries of the inequality 2 < x ≤ 8, and the highlighted area corresponds to the set of values of x, which are solutions of the inequality 2 < x ≤ 8.
Point 2, which is the left boundary of the half-interval, is shown as an empty circle because the left boundary of the inequality 2 < x ≤ 8 does not belong to the set of its solutions.
The point 8, which is the right boundary of the half-interval, is shown as a filled circle, because the right boundary of the inequality 2 < x ≤ 8 belongs to the set of its solutions.
In writing, the half-interval given by the inequality a < x ≤ b is denoted as follows: ( a ; b ]. Let us write the answer to the inequality 2 < x ≤ 8 using this notation:
x ∈ ( 2 ; 8 ]
This expression says that all numbers from 2 to 8, excluding the number 2 but including the number 8, are solutions to the inequality 2 < x ≤ 8.
Representation of number intervals on the coordinate line
The numerical interval can be given by an inequality or by a notation (round or square brackets). In both cases you should be able to represent this numerical interval on a coordinate line. Let's take a few examples.
Example 1. Represent the numerical interval given by the inequality x > 5
Recall that the inequality of the form x > a defines an open ray of numbers. In this case, the variable a is 5. The inequality x > 5 is strict, so the boundary 5 will be represented as an empty circle. We are interested in all values of x that are greater than 5, so the whole area to the right will be highlighted with strokes:

Example 2. Draw a number interval (5; +∞) on the coordinate line
This is the same numeric interval as in the previous example. But this time it is not defined by an inequality, but by the notation of a numerical interval.
Border 5 is framed by a parenthesis, so it doesn't belong to the gap. Consequently, the circle remains empty.
The symbol +∞ indicates that we are interested in all numbers greater than 5. Accordingly, the entire area to the right of the boundary 5 is highlighted with strokes:

Example 3. Draw a number interval (-5; 1) on the coordinate line.
Round brackets on both sides denote intervals. The boundaries of the interval do not belong to it, so the boundaries -5 and 1 will be represented on the coordinate line as empty circles. The entire area between them will be highlighted with strokes:

Example 4. Draw a number interval given by the inequality -5 < x < 1
This is the same numeric interval as in the previous example. But this time it is not defined by the notation of a gap, but by a double inequality.
An interval is defined by an inequality of the form a < x < b. In this case, the variable a equals -5, and the variable b equals one. The inequality -5 < x < 1 is strict, so the boundaries -5 and 1 will be represented as empty circles. We are interested in all values of x that are greater than -5 but less than one, so the entire area between -5 and 1 will be highlighted with strokes:

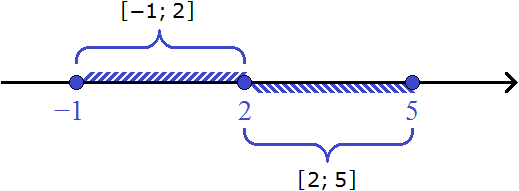
Example 5. Draw the numbers intervals [-1; 2] and [2; 5] on the coordinate line
This time we draw two intervals on the coordinate line at once.
Square brackets on both sides denote intervals. The borders of the segment belong to it, so the borders of segments [-1; 2] and [2; 5] will be represented on the coordinate line as filled circles. The entire area between them will be highlighted with strokes.
To clearly see the intervals [-1; 2] and [2; 5], you can draw the first one on the upper area, and the second one on the lower area. This is what we will do:
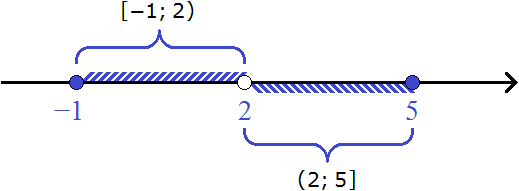
Example 6. On the coordinate line represent the number intervals [-1; 2) and (2; 5].
A square bracket on one side and a round bracket on the other side denote half-intervals. One of the boundaries of the half-interval belongs to it, and the other does not.
In the case of the half-interval [-1; 2], the left boundary belongs to it, and the right boundary does not. That means the left boundary will be drawn as a filled circle. The right boundary will be drawn as an empty circle.
In the case of half-interval (2; 5) it will belong only to the right boundary, while the left boundary will not. That means the left boundary will be drawn as an empty circle. The right boundary will be a filled circle.
Let us represent the interval [-1; 2] on the upper region of the coordinate line, and the interval (2; 5] on the lower one:
Examples of solving inequalities
An inequality that can be transformed to the form ax > b (or to the form ax < b) will be called a linear inequality with one variable.
In a linear inequality ax > b, x is the variable whose values are to be found, a is the coefficient of that variable, b is the boundary of the inequality, which, depending on the sign of the inequality, may or may not belong to the set of its solutions.
For example, the inequality 2x > 4 is an inequality of the form ax > b. The variable a is number 2, and the variable b (the boundaries of the inequality) is number 4.
The inequality 2x > 4 can be made even simpler. If we divide both parts of it by 2, we get an inequality x > 2
The resulting inequality x > 2 is also an inequality of the form ax > b, i.e. a linear inequality with one variable. In this inequality, the variable a is one. Earlier we said that coefficient 1 is not written down. And the variable b is the number 2.
Starting from this information, we will try to solve some simple inequalities. During the solution, we will perform elementary identity transformations in order to obtain an inequality of the form ax > b
Example 1. Solve the inequality x - 7 < 0
Add the number 7 to both parts of the inequality
x − 7 + 7 < 0 + 7
The left part will remain x, and the right part will become 7
x < 7
By elementary transformations we reduced the inequality x - 7 < 0 to an equivalent inequality x < 7. Solutions of the inequality x < 7 are all numbers less than 7. The boundary 7 does not belong to the set of solutions because the inequality is strict.
When an inequality is reduced to the form x < a (or x > a), it can be considered as already solved. Our inequality x - 7 < 0 is also reduced to this form, namely x < 7. But most schools require that the answer be written using a number space and illustrated on a coordinate line.
Let us write down the answer using a numeric interval. In this case the answer is an open number ray (recall that the number ray is given by the inequality x < a and is denoted as ( -∞ ; a)
x ∈ ( −∞ ; 7 )
On the coordinate line, boundary 7 will be shown as an empty circle, and all the area to the left of the boundary will be highlighted with strokes:
![]()
To check, take any number from the interval ( -∞ ; 7 ) and substitute it into the inequality x < 7 instead of the variable x. For example, take the number 2
2 < 7
We got a correct numerical inequality, so the solution is correct. Take any other number, for example, the number 4
4 < 7
The numerical inequality is correct. So the solution is correct.
And since the inequality x < 7 is equivalent to the original inequality x - 7 < 0, the solutions of the inequality x < 7 will coincide with the solutions of the inequality x - 7 < 0. Substitute the same test values 2 and 4 in the inequality x - 7 < 0
2 − 7 < 0
−5 < 0 — Correct inequality
4 − 7 < 0
−3 < 0 Correct inequality
Example 2. Solve the inequality -4x < -16
Divide both parts of the inequality by -4. Remember that when you divide both parts of an inequality by a negative number, the sign of the inequality is reversed:
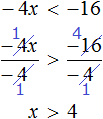
We reduced the inequality -4x < -16 to an equivalent inequality x > 4. Solutions of the inequality x > 4 will be all numbers that are greater than 4. The boundary 4 does not belong to the set of solutions because the inequality is strict.
Let's represent the set of solutions to the inequality x > 4 on the coordinate line and write the answer as a numeric interval:
![]()
![]()
Example 3. Solve the inequality 3y + 1 > 1 + 6y
Change the sign of 6y from the right hand side to the left hand side. Move 1 from the left hand side to the right hand side, again changing the sign:
3y − 6y> 1 − 1
Let's give like terms:
−3y > 0
Divide both parts by -3. Remember that when you divide both parts of an inequality by a negative number, the sign of the inequality is reversed:
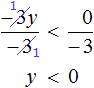
The solutions of the inequality y < 0 are all numbers less than zero. Draw the set of solutions of the inequality y < 0 on the coordinate line and write the answer as a numerical interval:

![]()
Example 4. Solve the inequality 5(x - 1) + 7 ≤ 1 - 3(x + 2)
Open the brackets in both parts of the inequality:
![]()
Move -3x from the right side to the left side, changing the sign. Move terms -5 and 7 from the left side to the right side, again changing the signs:
![]()
Let's give like terms:
![]()
Divide both parts of the resulting inequality by 8
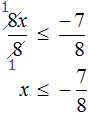
Solutions of the inequality ![]() are all numbers that are less than
are all numbers that are less than ![]() . The boundary
. The boundary ![]() belongs to the set of solutions, because the inequality
belongs to the set of solutions, because the inequality ![]() is non-strict.
is non-strict.
Let's represent the set of solutions to the inequality ![]() on the coordinate line and write the answer as a numeric interval:
on the coordinate line and write the answer as a numeric interval:

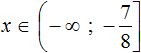
Example 5. Solve an inequality ![]()
Multiply both parts of the inequality by 2. This will get rid of the fraction on the left side:
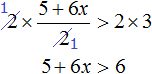
Now move 5 from the left part to the right part, changing the sign:
![]()
After adding like terms, we obtain the inequality 6x > 1. Divide both parts of this inequality by 6. Then we obtain:
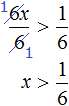
The solutions of the inequality ![]() are all numbers that are greater than
are all numbers that are greater than ![]() . The boundary of
. The boundary of ![]() does not belong to the set of solutions, because the inequality
does not belong to the set of solutions, because the inequality ![]() is strict.
is strict.
Let's represent the set of solutions to the inequality ![]() on the coordinate line and write the answer as a numeric interval:
on the coordinate line and write the answer as a numeric interval:

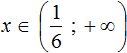
Example 6. Solve an inequality ![]()
Multiply both parts by 6
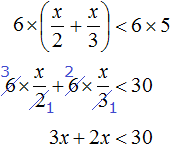
After adding like terms, we obtain the inequality 5x < 30. Divide both parts of this inequality by 5
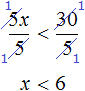
Solutions of the inequality x < 6 are all numbers that are less than 6. The boundary 6 does not belong to the set of solutions, because the inequality is x < 6 strict.
Let's represent the set of solutions to the inequality x < 6 on the coordinate line and write the answer as a numerical interval:
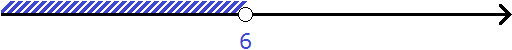
![]()
Example 7. Solve an inequality ![]()
Multiply both parts of the inequality by 10
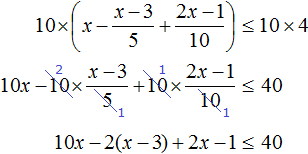
In the resulting inequality, open the brackets on the left side:
![]()
Move the terms without x to the right side
![]()
Let us give like terms in both parts:
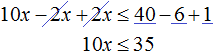
Divide both parts of the resulting inequality by 10
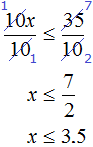
Solutions of the inequality x ≤ 3.5 are all numbers that are less than 3.5. The boundary 3.5 belongs to the set of solutions, because the inequality x ≤ 3.5 is non-strict.
Let us represent the set of solutions of the inequality x ≤ 3.5 on the coordinate line and write the answer as a numerical interval:

![]()
Example 8. Solve an inequality 4 < 4x < 20
To solve such an inequality, we need to free the variable x from the coefficient 4. Then we will be able to tell in what interval is the solution to this inequality.
To free the variable x from the coefficient, we can divide the term 4x by 4. But the rule in inequalities is that if we divide a term of an inequality by any number, then we have to do the same with the other terms that are part of the given inequality. In our case, all three terms of the inequality 4 < 4x < 20 must be divided by 4.
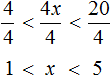
Solutions of the inequality 1 < x < 5 are all numbers that are greater than 1 and less than 5. Boundaries 1 and 5 do not belong to the set of solutions, because the inequality 1 < x < 5 is strict.
Let's represent the set of solutions to the inequality 1 < x < 5 on the coordinate line and write the answer as a number space:

![]()
Example 9. Solve the inequality -1 ≤ -2x ≤ 0
Divide all terms of the inequality by -2
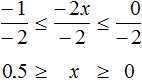
We obtained the inequality 0.5 ≥ x ≥ 0. It is desirable to write a double inequality so that the smaller term is on the left and the larger one is on the right. Therefore we rewrite our inequality as follows:
0 ≤ x ≤ 0.5
Solutions of the inequality 0 ≤ x ≤ 0.5 are all numbers that are greater than 0 and less than 0.5. The boundaries 0 and 0.5 belong to the set of solutions, because the inequality 0 ≤ x ≤ 0.5 is not strict.
Let us represent the set of solutions to the inequality 0 ≤ x ≤ 0.5 on the coordinate line and write the answer as a number space:

![]()
Example 10. Solve an inequality ![]()
Multiply both inequalities by 12
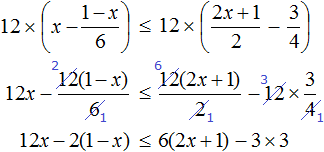
Open the brackets in the resulting inequality and give like terms:
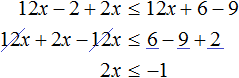
Divide both parts of the resulting inequality by 2
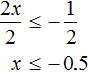
Solutions of the inequality x ≤ -0.5 are all numbers that are less than -0.5. The boundary -0.5 belongs to the set of solutions, since the inequality x ≤ -0.5 is not strict.
Let us represent the set of solutions to the inequality x ≤ -0.5 on the coordinate line and write the answer as a number space:

![]()
Example 11. Solve an inequality ![]()
Multiply all parts of the inequality by 3
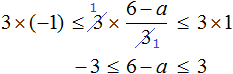
Now subtract 6 from each part of the resulting inequality
![]()
Divide each part of the resulting inequality by -1. Remember that when you divide all parts of an inequality by a negative number, the sign of the inequality is reversed:
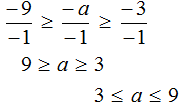
Solutions of the inequality 3 ≤ a ≤ 9 are all numbers that are greater than 3 and less than 9. Boundaries 3 and 9 belong to the set of solutions, because the inequality 3 ≤ a ≤ 9 is non-strict.
Let us represent the set of solutions of the inequality 3 ≤ a ≤ 9 on the coordinate line and write the answer as a numerical interval:

![]()
When there are no solutions
There are inequalities that have no solutions. Such, for example, is the inequality 6x > 2(3x + 1). As we solve this inequality, we will come to the conclusion that the sign of the inequality > does not justify its location. Let's see how that looks.
Open the brackets in the right part of this inequality, and we obtain 6x > 6x + 2. Transfer 6x from the right side to the left side, changing the sign, we get 6x - 6x > 2. We give like terms and obtain the inequality 0 > 2, which is not true.
For better understanding, let's rewrite the reduction of like terms in the left part as follows:
![]()
We obtained the inequality 0x > 2. On the left side there is a product which will be equal to zero for any x. And zero cannot be greater than number 2. So the inequality 0x > 2 has no solutions.
And if the given equational inequality 0x > 2 has no solutions, then the original inequality 6x > 2(3x + 1) has no solutions either.
Example 2. Solve an inequality ![]()
Multiply both parts of the inequality by 3
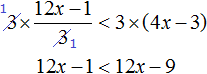
In the resulting inequality, move the term 12x from the right side to the left side, changing the sign. Then we give like terms:
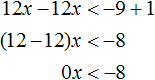
The right side of the resulting inequality for any x will be zero. And zero is not less than -8. So the inequality 0x < -8 has no solutions.
And if the above equational inequality 0x < -8 has no solutions, then the original inequality ![]() has no solutions either
has no solutions either
Answer: is that there are no solutions.
When there are infinitely many solutions
There are inequalities that have infinitely many solutions. Such inequalities become true for any x.
Example 1. Solve the inequality 5(3x - 9) < 15x
Open the brackets in the right part of the inequality:
![]()
Let's move 15x from the right part to the left part, changing the sign:
![]()
Let us give like terms in the left part:
![]()
We obtained the inequality 0x < 45. On the left hand side there is a product which will be equal to zero for any x. And zero is less than 45. So the solution of the inequality 0x < 45 is any number.
And if the above equational inequality 0x < 45 has innumerable solutions, then the original inequality 5(3x - 9) < 15x has the same solutions.
The answer can be written as a numerical interval:
x ∈ ( −∞; +∞ )
This expression says that the solutions to the inequality 5(3x - 9) < 15x are all numbers from minus infinity to plus infinity.
Example 2. Solve the inequality: 31(2x + 1) - 12x > 50x
Open the brackets on the left side of the inequality:
![]()
Move 50x from the right side to the left side, changing the sign. And move the term 31 from the left part to the right part, again changing the sign:
![]()
Let's give like terms:
![]()
We obtained the inequality 0x > -31. On the left side there is a product which will be equal to zero for any x. And zero is greater than -31. So the solution of the inequality 0x < -31 is any number.
And if the above equational inequality 0x > -31 has innumerable solutions, then the original inequality 31(2x + 1) - 12x > 50x has the same solutions.
Let us write the answer in the form of a numerical interval:
x ∈ ( −∞; +∞ )
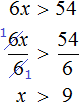

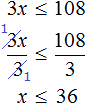
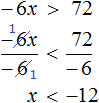
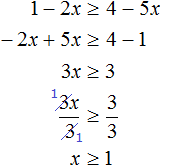
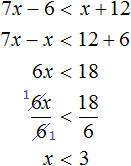
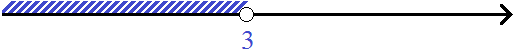
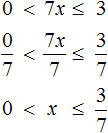

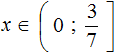
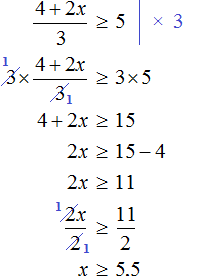

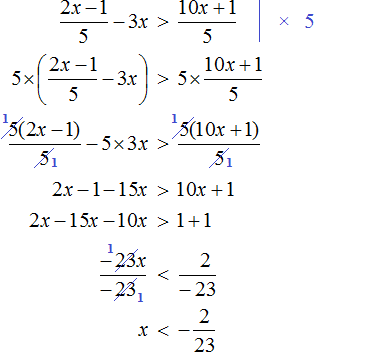

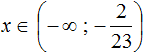
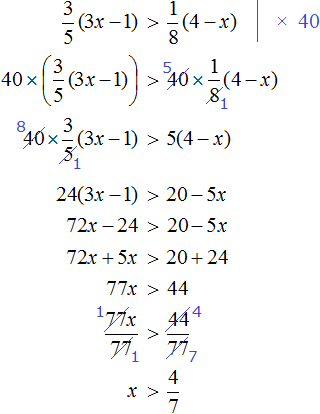

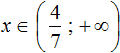
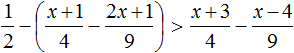
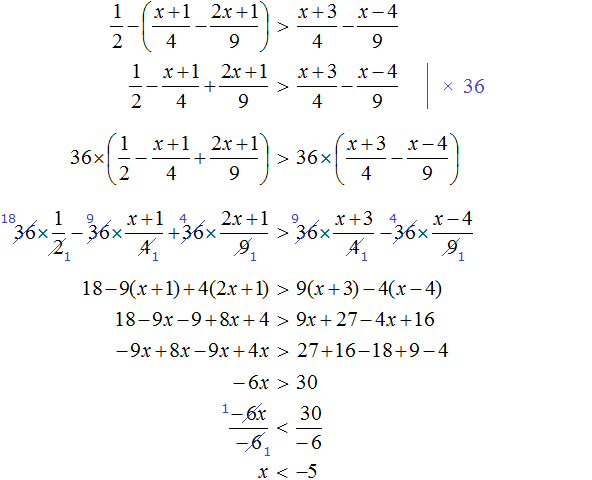
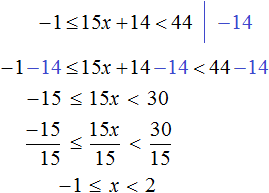


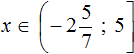
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.