Distributive law of multiplication

Definition. The distributive law of multiplication says that any number which is multiplied by the sum of two or more numbers is equal to the sum of that number multiplied by each of the numbers separately.

Consider the following expression:

(3 + 5) × 2

We know that we must first perform the action in parentheses. We do it:

(3 + 5) = 8

In the main expression (3 + 5) × 2, replace the expression in parentheses with the resulting eight:

8 × 2 = 16

The answer is 16. The same example can be solved using the distributive law of multiplication. To do this, multiply each summand in parentheses by 2, then add the results:

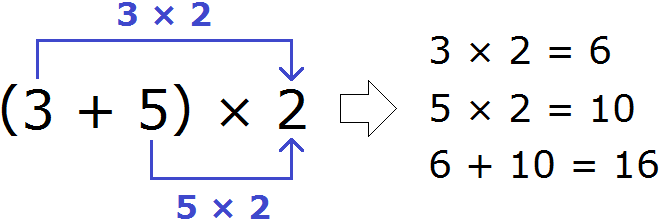
We have looked at the distributive law of multiplication in too much detail. At school, this example would have been recorded very briefly. You need to get used to this kind of notation, too. It looks like this:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

Or even shorter:

(3 + 5) × 2 = 6 + 10 = 16

Now let's write down the distributive law of multiplication using variables:

(a + b) × c = a × c + b × c

Let's look carefully at the beginning of this distributive law of multiplication. Its beginning looks like this: (a + b) × c.

If we consider the expression in parentheses (a + b) as a whole, it will be a multiplier, and the variable c will be a multiplier because they are connected by the multiplication sign ×

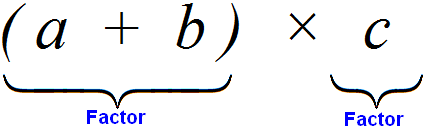
From the commutative law of multiplication we learned that if we swap the first factor and the second, the product does not change.

If we swap the factor (a + b) and the factor c, we get the expression c × (a + b). Then we multiply the variable c by the sum of (a + b). To do this multiplication, we apply the distributive law of multiplication. In this case, the variable c must be multiplied by each summand in parentheses:

c × (a + b) = c × a + c × b

Example 2. Find the value of the expression 5 × (3 + 2)

Multiply the number 5 by each summand in parentheses and add the results:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Example 3. Calculate 6 × (5 + 2)

Multiply 6 by each summand in parentheses and add the results:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

If the parentheses are not the sum but the difference, you must first multiply the multiplier by each number that is in the parentheses. Then subtract the second number from the first number. In principle, there is nothing new.

Example 4. Find the value of the expression 5 × (6 - 2)

Multiply 5 by each number in parentheses. Then subtract the second number from the first number:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Example 5. Calculate 7 × (3 - 2)

Multiply 7 by each number in parentheses. Then subtract the second number from the first number:

7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7

Add comment