We continue to learn about division. In this lesson we will look at concepts such as GCD and LCM.
Definition. GCD is the greatest common divisor. (or greatest common factor)
Definition. LCM is the least common multiple.
It's a pretty boring topic, but it's a must-have. Without understanding this topic, you will not be able to work effectively with fractions, which are a real obstacle in math.
Greatest common divisor
Definition. The greatest common divisor of a and b is the greatest number by which a and b are both divided without a remainder.
To understand this definition well, substitute any two numbers instead of variables a and b. For example, instead of the variable a we use the number 12, and instead of the variable b we use the number 9. Now let's try to read this definition:
The greatest common divisor of 12 and 9 is the greatest number by which 12 and 9 are divided without a remainder..
It is clear from the definition that we are talking about the common divisor of the numbers 12 and 9. The divisor is the greatest of all existing divisors. This greatest common divisor (GCD) must be found.
There are three ways to find the greatest common divisor of two numbers. The first way is quite time consuming, but it gives you a good understanding of the subject and a sense of its meaning.
The second and third ways are quite simple and allow you to quickly find the GCD. Consider all three methods. It is up to you to choose which one to use in practice.
The first way is to find all possible divisors of two numbers and to choose the greatest of them. Consider this method for the following example: find the greatest common divisor of 12 and 9.
First, find all possible divisors of 12. To do this, divide 12 by all the divisors between 1 and 12. If the divisor allows us to divide 12 without a remainder, we will highlight it in blue and make a corresponding explanation in parentheses.
12 : 1 = 12
(12 is divided by 1 without a remainder, so 1 is a divisor of 12.)
12 : 2 = 6
(12 divided by 2 without a remainder, so 2 is a divisor of 12.)
12 : 3 = 4
(12 divided by 3 without a remainder, so 3 is a divisor of 12.)
12 : 4 = 3
(12 divided by 4 without a remainder, so 4 is a divisor of 12.)
12 : 5 = 2 (2 in the remainder)
(12 is not divided by 5 without a remainder, so 5 is not a divisor of 12.)
12 : 6 = 2
(12 is divided by 6 without a remainder, so 6 is a divisor of 12.)
12 : 7 = 1 (5 in the remainder)
(12 is not divided by 7 without a remainder, so 7 is not a divisor of 12.)
12 : 8 = 1 (4 in the remainder)
(12 is not divided by 8 without a remainder, so 8 is not a divisor of 12.)
12 : 9 = 1 (3 in the remainder)
(12 is not divided by 9 without a remainder, so 9 is not a divisor of 12.)
12 : 10 = 1 (2 in the remainder)
(12 is not divided by 10 without a remainder, so 10 is not a divisor of 12.)
12 : 11 = 1 (1 in the remainder)
(12 is not divided by 11 without a remainder, so 11 is not a divisor of 12.)
12 : 12 = 1
(12 divided by 12 without a remainder, so 12 is a divisor of 12.)
Now let's find the divisors of 9. To do this, check all divisors from 1 to 9
9 : 1 = 9
(9 is divisible by 1 without a remainder, so 1 is a divisor of 9.)
9 : 2 = 4 (1 in the remainder)
(9 is not divided by 2 without a remainder, so 2 is not a divisor of 9.)
9 : 3 = 3
(9 is divisible by 3 without a remainder, so 3 is a divisor of 9.)
9 : 4 = 2 (1 in the remainder)
(9 is not divisible by 4 without a remainder, so 4 is not a divisor of 9.)
9 : 5 = 1 (4 in the remainder)
(9 is not divisible by 5 without a remainder, so 5 is not a divisor of 9.)
9 : 6 = 1 (3 in the remainder)
(9 is not divisible by 6 without a remainder, so 6 is not a divisor of 9.)
9 : 7 = 1 (2 in the remainder)
(9 is not divisible by 7 without a remainder, so 7 is not a divisor of 9.)
9 : 8 = 1 (1 in the remainder)
(9 is not divisible by 8 without a remainder, so 8 is not a divisor of 9.)
9 : 9 = 1
(9 is divisible by 9 without a remainder, so 9 is a divisor of 9.)
Now write down the divisors of both numbers. The numbers highlighted in blue are the divisors. Let's write them out:
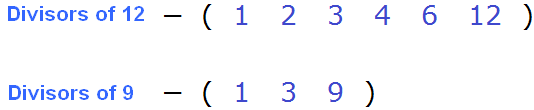
By writing out the divisors, you can immediately determine which is the largest and most common.
By definition, the greatest common divisor of 12 and 9 is the number by which 12 and 9 are divided without a remainder. The greatest and common divisor of 12 and 9 is the number 3
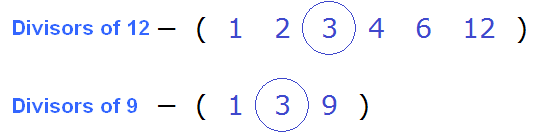
Both the number 12 and the number 9 are divided by 3 without a remainder:
12 : 3 = 4
9 : 3 = 3
So the GCD (12 and 9) = 3
The second way to find the GCD
Now consider the second method of finding the greatest common divisor. The essence of this method is to decompose both numbers into prime factors and multiply the common ones.
Example 1. Find the GCD of numbers 24 and 18
First, decompose both numbers into prime factors:
Now multiply their common factors. To avoid confusion, the common factors can be underlined.
Let's look at the decomposition of the number 24. Its first factor is 2. We look for the same factor in the expansion of 18 and we see that it is there too. Underline both twos:
Again we look at the decomposition of the number 24. Its second factor is also 2. Look for the same factor in the expansion of 18 and see that it is not there for the second time. Then we do not underline anything.
The next two in the expansion of 24 is also missing in the expansion of 18.
Move on to the last multiplier in the expansion of 24. We look for the same factor in the expansion of 18 and we see that it is there too. Underline both triples:
So, the common factors of 24 and 18 are multipliers 2 and 3. These multipliers must be multiplied to obtain the GCD:
2 × 3 = 6
So the GCD (24 and 18) = 6
The third way to find the GCD
Now consider the third method of finding the greatest common divisor. The essence of this method is that the numbers subject to the search for the greatest common divisor are decomposed into prime factors. Then from the expansion of the first number to cross out the multipliers that are not included in the expansion of the second number. The remaining numbers in the first expansion are multiplied and obtained GCD.
Example 1. Find the GCD of 28 and 16.
First, we decompose 28 and 16 into prime factors:
We got two decompositions: 
Now we remove from the expansion of the first number the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include a seven. And we cross it out of the first expansion:
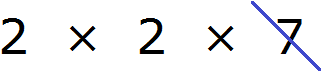
Now multiply the remaining multipliers and get the GCD:
The number 4 is the greatest common divisor of 28 and 16. Both of these numbers divide by 4 without a remainder:
28 : 4 = 7
16 : 4 = 4
GCD (28 and 16) = 4
Example 2. Find the GCD of numbers 100 and 40
Decompose the number 100 into factors
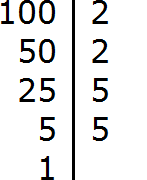
Decompose the number 40 into factors
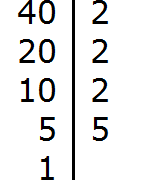
We got two decompositions: 2 × 2 × 5 × 5 and 2 × 2 × 2 × 5
Now from the expansion of the first number cross out the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include one five (there is only one five). We will cross it out of the first expansion
Multiply the remaining numbers:
The answer is 20, so 20 is the greatest common divisor of 100 and 40. These two numbers are divided by 20 without a remainder:
100 : 20 = 5
40 : 20 = 2
GCD (100 and 40) = 20.
Example 3. Find the GCD of numbers 72 and 128
Decompose the number 72 into factors
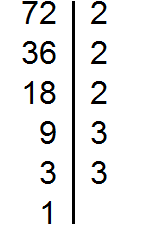
Decompose the number 128 into factors
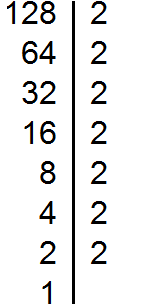2 × 2 × 2 × 3 × 3 and 2 × 2 × 2 × 2 × 2 × 2 × 2.
Now from the expansion of the first number cross out the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include two triples (they are not there at all). We cross them out of the first expansion:
Multiply the remaining numbers:
The answer is 8. So the number 8 is the greatest common divisor of 72 and 128. These two numbers are divided by 8 without a remainder:
72 : 8 = 9
128 : 8 = 16
GCD (72 and 128) = 8
Finding GCD for multiple numbers
The greatest common divisor can also be found for several numbers, not just for two. For this purpose, the numbers subject to the search for the greatest common divisor, decompose into prime factors, then find the product of the common prime factors of these numbers.
For example, find the GCD for numbers 18, 24, and 36
Decompose the number 18 into factors
Decompose the number 24 into factors
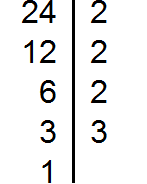
Decompose number 36 into factors
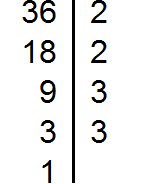
We got three decompositions:
Now find and underline the common factors:
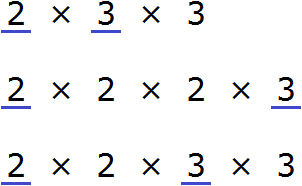
We see that the common factors for the numbers 18, 24, and 36 are multipliers 2 and 3. These multipliers are included in all three decompositions. By multiplying these multipliers, we get the GCD we are looking for:
2 × 3 = 6
The answer is 6. So 6 is the greatest common divisor of 18, 24, and 36. These three numbers are divided by 6 without a remainder:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
GCD (18, 24 and 36) = 6
Example 2. Find GCD for numbers 12, 24, 36 and 42
Decompose each number into prime factors. Then find the product of common prime factors.
Decompose the number 12 into factors
Decompose the number 24 into factors
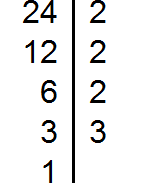
Decompose number 36 into factors
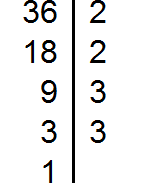
Decompose number 42 into factors
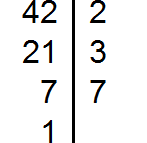
We got four decompositions:
Now find and underline the common factors:
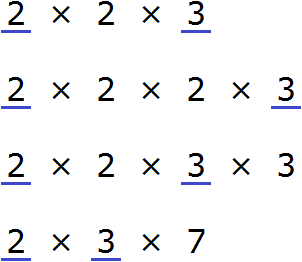
We see that the common factors for the numbers 12, 24, 36, and 42 are multipliers 2 and 3. By multiplying these multipliers, we get the GCD we are looking for:
2 × 3 = 6
The answer is 6. So 6 is the greatest common divisor of 12, 24, 36, and 42. These numbers are divided by 6 without a remainder:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
GCD (12, 24 , 36 and 42) = 6
Least common multiple
From the previous lesson we know that if any number is divisible by another number without a remainder, it is called a multiple of that number.
It turns out that a multiple can be common to several numbers. And now we will be interested in the multiple of two numbers, and it should be as small as possible.
Definition. The least common multiple (LCM) of a and b is the smallest number that is a multiple of a and b. In other words, it is the smallest number that is divisible without a remainder by a and b.
The definition contains two variables a and b. Let's substitute any two numbers for these variables. For example, instead of variable a, let's substitute number 9, and instead of variable b, let's substitute number 12. Now let's try to read the definition:
The least common multiple (LCM) of 9 and 12 is the smallest number that is a multiple of 9 and 12. In other words, it is the smallest number that is divisible without a remainder by 9 and by 12..
From the definition it is clear that the smallest common multiple is the smallest number that is divisible without a remainder by 9 and by 12. This least common multiple must be found.
There are three ways to find the least common multiple (LCM). The first method is to write out the first multiples of two numbers, and then choose among those multiples a number that is common to both numbers and is small. Let's apply this method.
First, find the first multiples of 9. To find multiples of 9, multiply this nine by numbers from 1 to 9 one by one. The answers will be multiples of 9.
So, let's begin. The multiples will be highlighted in blue:
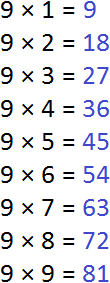
Now we find multiples for number 12. To do this, multiply the number 12 by all the numbers 1 to 12 in turn:
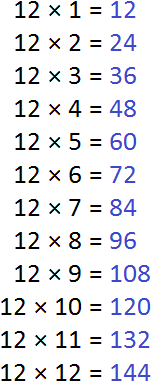
Now write out multiples of both numbers:
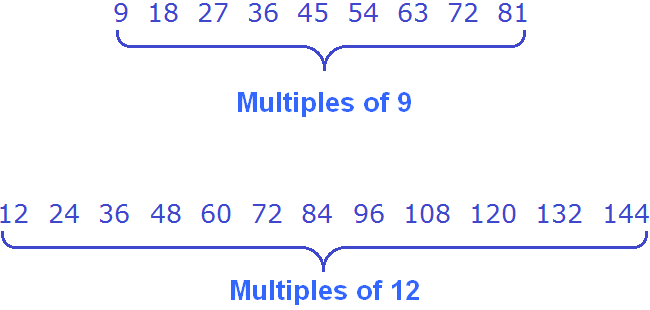
Now find the common multiples of both numbers. Once we find them, let's underline them at once:
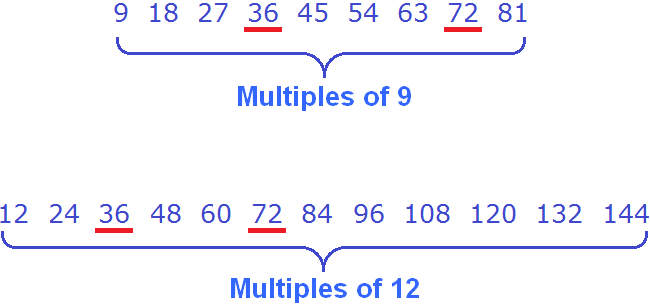
Common multiples of 9 and 12 are multiples of 36 and 72. The smallest of them is 36.
So the smallest common multiple of 9 and 12 is 36. This number is divisible by 9 and 12 without a remainder:
36 : 9 = 4
36 : 12 = 3
LCM (9 and 12) = 36
The second way to find the LCM
The second way is that the numbers for which we are looking for the least common multiple are decomposed into prime factors. Then write out the multipliers included in the first expansion, and add the missing multipliers from the second expansion. The resulting multipliers are multiplied and obtained LCM.
Let us apply this method to the previous problem. Find the LCM for numbers 9 and 12.
Decompose number 9 into factors
Decompose the number 12 into factors
Let us write out the first decomposition:
Now add the multipliers from the second expansion, which are absent in the first expansion. The first expansion does not contain two twos. We add them:
Now multiply these multipliers:
The answer is 36. So the least common multiple of 9 and 12 is 36. This number is divisible by 9 and 12 without a remainder:
36 : 9 = 4
36 : 12 = 3
LCM (9 and 12) = 36
In simple terms, it all comes down to organizing a new decomposition with both decompositions at once. The decomposition of the first number 9 is the multipliers 3 and 3, and the decomposition of the second number 12 is the multipliers 2, 2 and 3.
Our task was to organize a new expansion which would include the expansion of number 9 and the expansion of number 12 at the same time. To do this, we wrote out the expansion of the first number and added to it the multipliers from the second expansion that were not in the first expansion. As a result, we got a new decomposition 3 × 3 × 2 × 2. It is easy to see that it includes the decomposition of 9 and the decomposition of 12
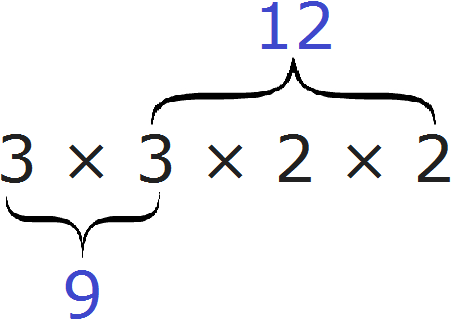
Example 2. Find the LCM of 50 and 180
Decompose the number 50 into factors
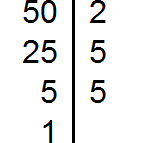
Decompose number 180 into factors
Let us write out the first decomposition:
Now add the multipliers from the second expansion, which are absent in the first expansion. The first expansion does not contain one more two and two threes. We add them:
Now multiply these multipliers:
The answer is 900. So the least common multiple of 50 and 180 is 900. This number is divisible by 50 and 180 without a remainder:
900 : 50 = 18
900 : 180 = 5
LCM (50 and 180) = 900
Example 3. Find the LCM of 8, 15, and 33
Decompose the number 8 into factors
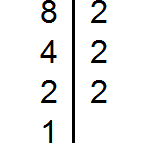
Decompose number 15 into factors
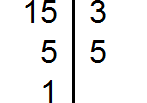
Decompose number 33 into factors
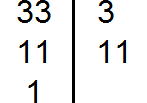
Let us write out the first decomposition:
Now add the factors from the second and third expansion, which are absent in the first expansion. Add the factors 3 and 5 from the second expansion, and the factor 11 from the third expansion:
Now multiply these multipliers:
The answer is 1320. So the least common multiple of 8, 15, and 33 is 1320. This number is divisible by 8, 15, and 33 without a remainder:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
LCM (8, 15and 33) = 1320
The third way to find the LCM
There is a third way to find the least common multiple. It works as long as it is searched for two numbers and as long as the greatest common divisor of those numbers is already found.
This method is more reasonable to use when you need to find the GCD and LCM of two numbers at the same time.
For example, let us find the GCD and LCM of the numbers 24 and 12. First, find the GCD of these numbers:
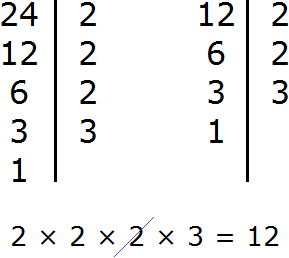
Now to find the least common multiple of 24 and 12, you need to multiply these two numbers and divide the result by their greatest common divisor.
So let's multiply the numbers 24 and 12
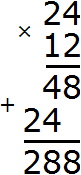
Divide the resulting number 288 by the GCD of numbers 24 and 12
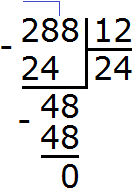
The answer is 24. So the least common multiple of 24 and 12 is 24.
LCM (24 and 12) = 24
Example 2. Find the GCD and LCM of 36 and 48
Find the GCD of 36 and 48
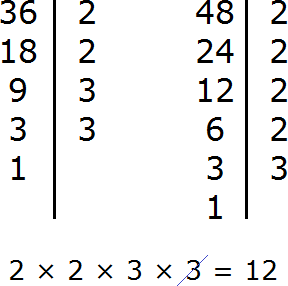
Multiply the numbers 36 and 48
Divide 1728 by the GCD of 36 and 48
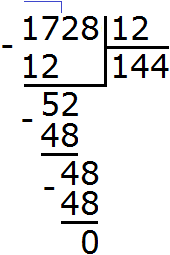
We got 144. So the least common multiple of 36 and 48 is 144.
LCM (36 and 48) = 144
To check, we can find the LCM by the usual second method we used before. If we have done everything correctly, we should get 144
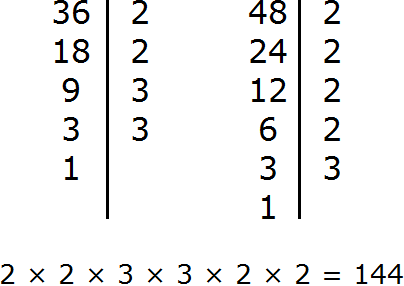
Don't get upset if you don't learn how to find GCD and LCM right away. The main thing is to understand what it is and how it works. And mistakes are quite natural at the beginning. As they say, "We learn by our mistakes.
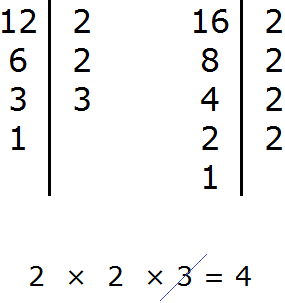
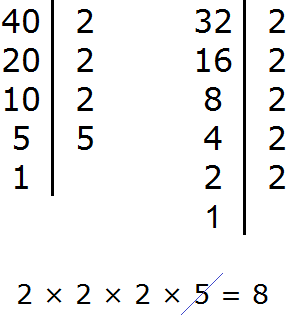
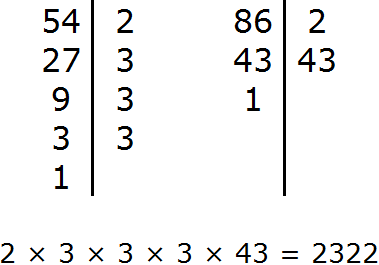
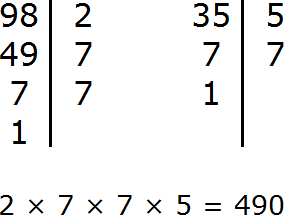
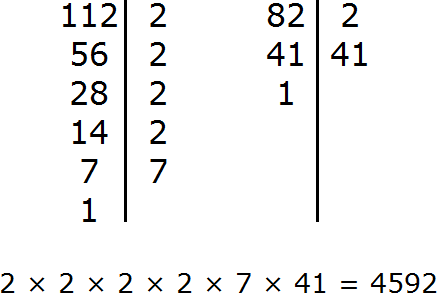
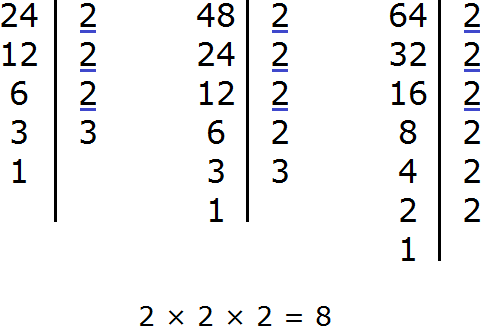
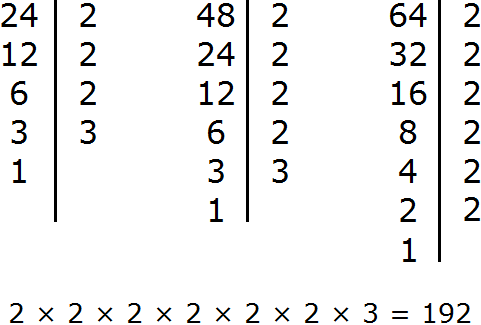
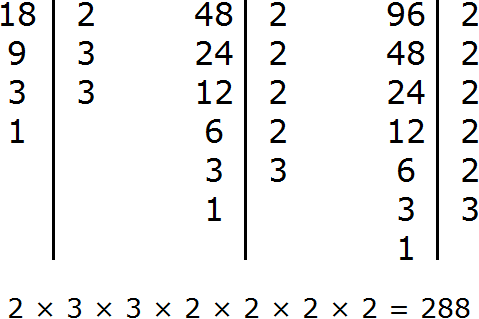
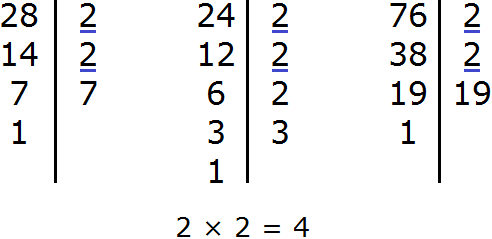
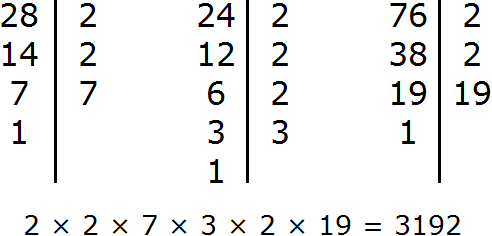
Comments