This lesson is about adding and subtracting rational numbers. The topic is a bit complex. Here we need to use the entire previously gained knowledge.
The rules of addition and subtraction of integers are also valid for rational numbers.
Recall that rational numbers are numbers that can be represented as fractions ![]() , where a is the numerator of the fraction and b is the denominator of the fraction. However, b must be not eqaul to zero.
, where a is the numerator of the fraction and b is the denominator of the fraction. However, b must be not eqaul to zero.
In this lesson we will increasingly refer to fractions and mixed numbers by one common phrase: rational numbers.
Adding rational numbers with different signs
Example 1. Find the value of the expression: ![]()
Put each rational number in parentheses together with its signs. Note that the plus sign in the expression is a sign of the operation and does not apply to fractions of ![]() . This fraction has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
. This fraction has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
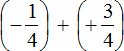
This is an addition of rational numbers with different signs.
To add rational numbers with different signs, you need to subtract the smaller modulus from the larger modulus, and put the sign of the rational number whose modulus is larger before the result you get.
And to understand which modulus is greater and which is less, you should be able to compare both modulus of these fractions before calculating them:
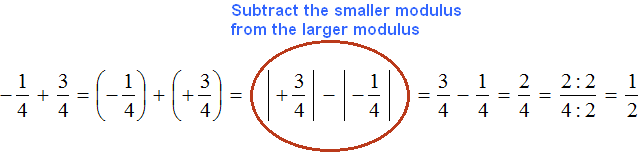
The modulus of the rational number ![]() is greater than the modulus of the rational number
is greater than the modulus of the rational number ![]() . Therefore, we subtracted
. Therefore, we subtracted ![]() from
from ![]() . The result is
. The result is ![]() . Then by reducing this fraction by 2, we get the final answer
. Then by reducing this fraction by 2, we get the final answer ![]() .
.
Some primitive operations, such as putting numbers in parentheses and modulus calculations can be skipped. This example may well be written in a shorter form:
![]()
Example 2. Find the value of the expression: ![]()
Put each rational number in parentheses together with its signs. Note that the minus between the rational numbers ![]() and
and ![]() is a sign of the operation and does not apply to the fraction
is a sign of the operation and does not apply to the fraction ![]() . This fraction has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
. This fraction has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
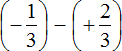
Replace subtraction with addition. Recall that to do this you must add to the subtractor the number opposite to the subtractor:
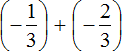
We have obtained the addition of negative rational numbers.
To add negative rational numbers, add their both modulus and put minus sign in front of the result:
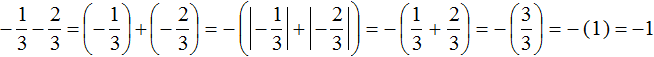
Let's write down the solution to this example in shorter form:
![]()
Note. It is not necessary to bracket each rational number. This is done for convenience, to see clearly what signs rational numbers have.
Example 3. Find the value of the expression: ![]()
In this expression, the fractions have different denominators. To make the exercise easier, let's reduce these fractions to a common denominator. We won't go into detail about how to do this. If you have trouble with it, be sure to revise lesson actions with fractions.
After reducing the fractions to a common denominator, the expression will take the following form:
![]()
Put each rational number in parentheses together with its signs:
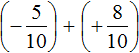
This is an addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and precede the answer with the sign of the rational number whose modulus is greater:
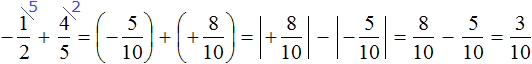
Let's write down the solution to this example in shorter form:

Example 4. Find the value of the expression: ![]()
Put each rational number in parentheses along with its signs:
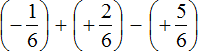
Let's calculate this expression in the following order: add the rational numbers ![]() and
and 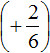 , then subtract the rational number
, then subtract the rational number ![]() from the result obtained.
from the result obtained. 
First act:
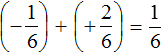
Second act:
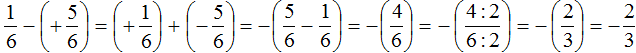
Thus, the value of ![]() equals
equals ![]()
![]()
Example 5. Find the value of the expression: ![]()
Let's represent the integer -1 as a fraction ![]() , and convert the mixed number
, and convert the mixed number ![]() to an improper fraction:
to an improper fraction:
![]()
Let's reduce these fractions to a common denominator. After reducing them to a common denominator, they will take the following form:
![]()
Put each rational number in parentheses along with its signs:

We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the answer:
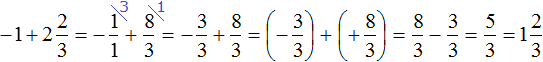
We got an answer of ![]() .
.
There is a second way to solve this problem. It consists in adding the whole parts separately.
So, let's go back to the original expression:
![]()
Let's put each number in parentheses.
To do this, temporarily expand the mixed number ![]() :
:
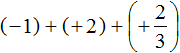
Let's calculate the whole parts:
(−1) + (+2) = 1
In the main expression instead of (-1) + (+2) write the resulting unit:
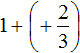
Let's convolve the resulting expression 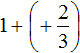 . To do this, write 1 and the fraction
. To do this, write 1 and the fraction ![]() together:
together:
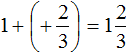
Let's write down the solution to this example in shorter form:
![]()
Example 6. Find the value of the expression: ![]()
Let's convert the mixed number ![]() to an improper fraction. Let's rewrite the rest of the fraction without changing it:
to an improper fraction. Let's rewrite the rest of the fraction without changing it:
![]()
Put each rational number in parentheses along with its signs:
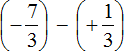
Replace subtraction with addition:
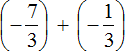
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the result:
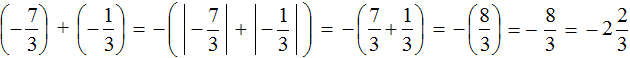
Let's write down the solution to this example in shorter form:
![]()
Example 7. Find the value of the expression: ![]()
Let's represent the integer -5 as a fraction ![]() , and let's convert the mixed number
, and let's convert the mixed number ![]() into an improper fraction:
into an improper fraction:
![]()
Let's reduce these fractions to a common denominator. After reducing them to a common denominator, they will take the following form:
![]()
Put each rational number in parentheses along with its signs:
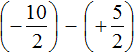
Replace subtraction with addition:
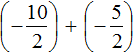
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus sign in front of the result:
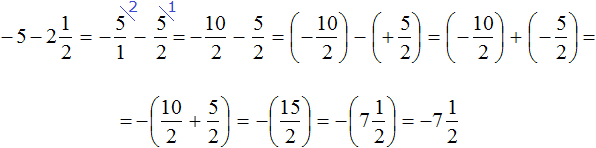
Thus, the value of expression ![]() is
is ![]() .
.
Let us solve this example in the second way. Let us return to the original expression:
![]()
Write down the mixed number ![]() in expanded form. Let's rewrite the rest without changes:
in expanded form. Let's rewrite the rest without changes:
![]()
Put each rational number in parentheses together with its signs:

Replace subtraction with addition where possible:
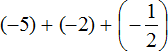
Let's calculate the whole parts:
![]()
In the main expression, instead of ![]() , write the resulting number -7
, write the resulting number -7
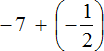
The expression 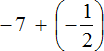 is an expanded form of the mixed number
is an expanded form of the mixed number ![]() . Write the number -7 and fraction
. Write the number -7 and fraction ![]() together to form the final answer:
together to form the final answer:
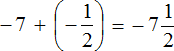
Let's write down the solution to this example in shorter form:
![]()
Example 8. Find the value of the expression: ![]()
Let's convert the mixed numbers into improper fraction:
![]()
Put each rational number in parentheses together with its signs:
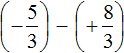
Replace subtraction with addition:
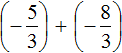
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the obtained answer:
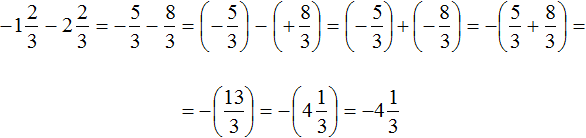
Thus, the value of expression ![]() is
is ![]()
This example can also be solved in the second way. It consists of adding the whole and fractional parts separately. Let's return to the original expression:
![]()
Put each rational number in parentheses along with its signs:
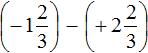
Replace subtraction with addition:
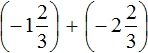
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the obtained answer. But this time we add the integers (-1 and -2) and the fractions ![]() and
and ![]() separately.
separately.

Let's write down the solution to this example in shorter form:
![]()
Example 9. Find the value of the expression: 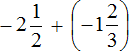
Let's convert the mixed numbers into improper fraction:

Put the rational number ![]() in parentheses together with its sign. Rational number
in parentheses together with its sign. Rational number ![]() does not need to be in parentheses because it is already in parentheses:
does not need to be in parentheses because it is already in parentheses:
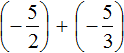
Let's reduce these fractions to a common denominator. After reducing them to a common denominator, they will take the following form:
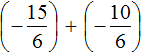
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the result:
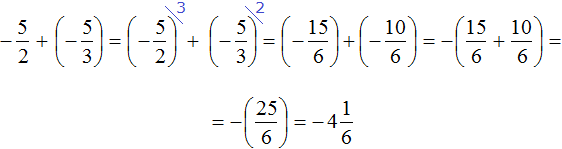
Thus, the value of expression 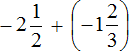 is
is ![]()
Now let's try to solve the same example in the second way, namely by adding the whole and fractional parts separately.
This time, in order to get a short solution, we will try to skip some steps, such as: writing the mixed number in expanded form and replacing subtraction with addition:
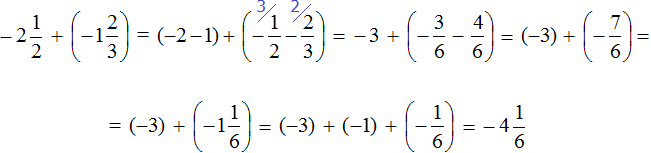
Note that the fractional parts have been reduced to a common denominator.
Example 10. Find the value of the expression: 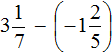
Replace subtraction with addition:
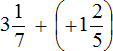
The resulting expression has no negative numbers, which are the main cause of errors. And since there are no negative numbers, we can remove the plus before the subtractor and also remove the parentheses:
![]()
We have obtained a simple expression, which is easy to calculate. Let's calculate it any way we want:
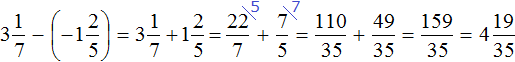
Example 11. Find the value of the expression: 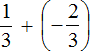
This is an addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the answer:
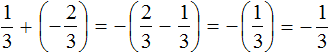
Example 12. Find the value of the expression: 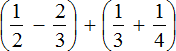
The expression consists of several rational numbers. According to the order of operations, you must perform what is inside the brackets first.
First calculate expression 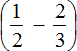 , then expression
, then expression 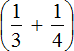 . Add the results obtained.
. Add the results obtained.
First act:
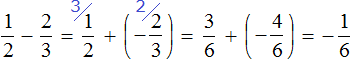
Second act:
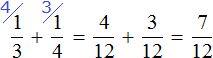
Third act:
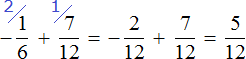
Answer: The value of the expression 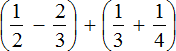 is
is ![]()
Example 13. Find the value of the expression: 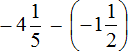
Let's convert the mixed numbers into improper fraction:
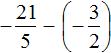
Put the rational number ![]() in parentheses together with its sign. Rational number
in parentheses together with its sign. Rational number ![]() does not need to be bracketed because it is already bracketed:
does not need to be bracketed because it is already bracketed:
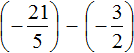
Let's reduce these fractions to a common denominator. After reducing them to a common denominator, they will take the following form:

Replace subtraction with addition:
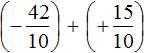
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the obtained result:
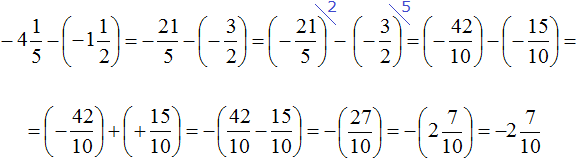
Thus, the value of expression 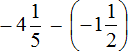 is
is ![]()
Consider addition and subtraction of decimals, which are also rational numbers and can be both positive and negative.
Example 14. Find the value of the expression -3.2 + 4.3
Put each rational number in parentheses together with its signs. Note that the plus sign given in the expression is a sign of the operation and does not apply to the decimal 4.3. This decimal has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
(−3.2) + (+4.3)
This is an addition of rational numbers with different signs.
To add rational numbers with different signs, you need to subtract the smaller modulus from the larger modulus, and put the sign of the rational number whose modulus is larger in front of the answer you get.
And to understand which modulus is greater and which is less, you need to be able to compare both modulus of these decimals before calculating them:
(−3.2) + (+4.3) = |+4.3| − |−3.2| = 1.1
The modulus of 4.3 is greater than the modulus of -3.2, so we subtracted 3.2 from 4.3. The answer is 1.1. The answer is positive because the answer must be preceded by the sign of the rational number whose modulus is greater. And the modulus of 4.3 is greater than the modulus of -3.2
Therefore, the value of -3.2 + (+4.3) is 1.1
This example can be written in a shorter form:
−3.2 + (+4.3) = 1.1
Example 15. Find the value of the expression 3.5 + (-8.3)
This is an addition of rational numbers with different signs. As in the previous example, subtract the smaller one from the larger modulus and put the sign of the rational number whose modulus is larger in front of the answer:
3.5 + (−8.3) = −(|−8.3| − |3.5|) = −(8.3 − 3.5) = −(4.8) = −4.8
Thus, the value of the expression 3.5 + (-8.3) is -4.8
This example can be written in shorter form:
3.5 + (−8.3) = −4.8
Example 16. Find the value of the expression -7.2 + (-3.11)
This is an addition of negative rational numbers. To add negative rational numbers, add their both modulus and put minus in front of the result.
Calcualtions with modules can be skipped:
−7.2 + (−3.11) = −7.20 + (−3.11) = −(7.20 + 3.11) = −(10.31) = −10.31
Thus, the value of the expression -7.2 + (-3.11) is -10.31
This example can be written in shorter form:
−7.2 + (−3.11) = −10.31
Example 17. Find the value of the expression -0.48 + (-2.7)
This is an addition of negative rational numbers. Add their modules and put a minus in front of the answer. You may omit both modulus, so as not to overload the expression:
−0.48 + (−2.7) = (−0.48) + (−2.70) = −(0.48 + 2.70) = −(3.18) = −3.18
Example 18. Find the value of the expression -4.9 - 5.9
Put each rational number in parentheses together with its signs. Note that the minus sign between the rational numbers -4.9 and 5.9 is an operation sign and does not apply to the number 5.9. This rational number has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
(−4.9) − (+5.9)
Replace subtraction with addition:
(−4,9) + (−5,9)
We obtained the addition of negative rational numbers. Add their modules and put minus in front of the obtained answer:
(−4.9) + (−5.9) = −(4.9 + 5.9) = −(10.8) = −10.8
Thus, the value of the expression -4.9 - 5.9 is -10.8
This example can be written in a shorter form:
−4.9 − 5.9 = −10.8
Example 19. Find the value of the expression 7 - 9.3
Bracket each number together with its signs
(+7) − (+9.3)
Replacing subtraction with addition
(+7) + (−9.3)
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the number whose modulus is greater in front of the result:
(+7) + (−9.3) = −(9.3 − 7) = −(2.3) = −2.3
Thus, the value of the expression 7 - 9.3 is -2.3
This example can be written in a shorter form:
7 − 9.3 = −2.3
Example 20. Find the value of the expression -0.25 - (-1.2)
Replace subtraction with addition:
−0.25 + (+1.2)
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the number whose modulus is greater in front of the answer:
−0.25 + (+1.2) = 1.2 − 0.25 = 0.95
This example can be written in a shorter form:
−0.25 − (−1.2) = 0.95
Example 21. Find the value of the expression -3.5 + (4.1 - 7.1)
Follow the steps in parentheses, then add the answer to the number -3.5
First act:
4.1 − 7.1 = (+4.1) − (+7.1) = (+4.1) + (−7.1) = −(7.1 − 4.1) = −(3.0) = −3.0
Second act:
−3.5 + (−3.0) = −(3.5 + 3.0) = −(6.5) = −6.5
Answer: The value of the expression -3.5 + (4.1 - 7.1) is -6.5
Example 22. Find the value of the expression (3.5 - 2.9) - (3.7 - 9.1)
Perform the actions in parentheses. Then subtract the number resulting from the first parentheses from the number resulting from the second parentheses:
First act:
3.5 − 2.9 = (+3.5) − (+2.9) = (+3.5) + (−2.9) = 3.5 − 2.9 = 0.6
Second act:
3.7 − 9.1 = (+3.7) − (+9.1) = (+3.7) + (−9.1) = −(9.1 − 3.7) = −(5.4) = −5.4
Third act:
0.6 − (−5.4) = (+0.6) + (+5.4) = 0.6 + 5.4 = 6.0 = 6
Answer: The value of the expression (3.5 - 2.9) - (3.7 - 9.1) is 6.
Example 23. Find the value of the expression -3.8 + 17.15 - 6.2 - 6.15
Bracket each rational number together with its signs
(−3.8) + (+17.15) − (+6.2) − (+6.15)
Replace subtraction with addition where possible:
(−3.8) + (+17.15) + (−6.2) + (−6.15)
An expression consists of several summands. According to the commutative law of addition, if an expression consists of several summands, the sum will not depend on the order of operations. This means that the summands can be added in any order.
So let's add up all the summands from left to right in the order of their order:
First act:
(−3.8) + (+17.15) = 17.15 − 3.80 = 13.35
Second act:
13.35 + (−6.2) = 13.35 − −6.20 = 7.15
Third act:
7.15 + (−6.15) = 7.15 − 6.15 = 1.00 = 1
Answer: The value of the expression -3.8 + 17.15 - 6.2 - 6.15 is 1.
Example 24. Find the value of the expression ![]()
Let's convert the decimal -1.8 to a mixed number. Let's rewrite the rest without changing:
![]()
Then we calculate this expression by applying the previously learned rules:
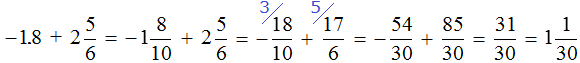
Example 25. Find the value of the expression ![]()
Replace subtraction with addition. At the same time, convert the decimal fraction (-4.4) into an improper fraction
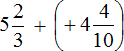
There are no negative numbers in the resulting expression. And since there are no negative numbers, we can remove the plus before the second number and remove the parentheses. Then we get a simple addition expression, which is easy to solve
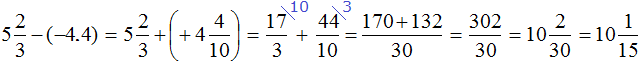
Example 26. Find the value of the expression ![]()
Convert the mixed number ![]() into an improper fraction, and the decimal -0.85 into a fraction. We obtain the following expression:
into an improper fraction, and the decimal -0.85 into a fraction. We obtain the following expression:
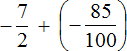
We obtained the addition of negative rational numbers. Add their modules and put minus in front of the obtained answer:

Example 27. Find the value of the expression 
Convert decimal and fraction into improper fractions.
To convert the decimal 2.05 to an improper fraction, you can first convert it to a mixed number and then to an improper fraction:
![]()
After converting them into improper fraction, we obtain the following expression:
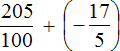
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus and precede the answer with the sign of the number whose modulus is greater:
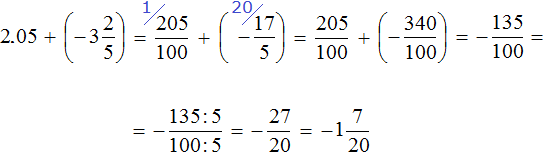
Example 28. Find the value of the expression ![]()
Replace subtraction with addition. Next, convert the decimal to fraction. Then calculate the resulting expression by applying the previously learned rules:
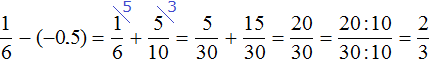
Example 29. Find the value of the expression 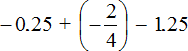
Convert the decimals -0.25 and -1.25 into fractions, and rewrite the rest unchanged. We obtain the following expression:
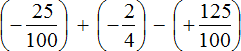
You can first replace subtraction with addition where possible and add rational numbers one by one.
There is a second option: first add the rational numbers 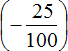 and
and ![]() , and then subtract
, and then subtract 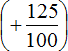 from the result. That's what we'll do.
from the result. That's what we'll do.
First act:
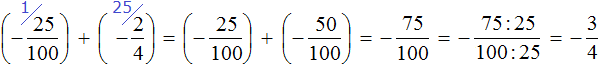
Second act:
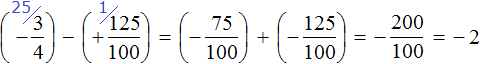
Answer: The value of expression 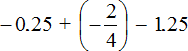 is −2
is −2
Example 30. Find the value of the expression
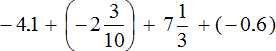
Convert the decimals into fractions. Let's rewrite the rest without changing:
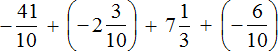
You have obtained the sum of several summands. If the sum is consist of several summands, the expression can be calculated in any order. This follows from the combinatorial law of addition.
So we can arrange the most convenient option for us. First of all, we can add the first and the last summand, namely the rational numbers ![]() and
and 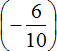 . These numbers have the same denominators, and so this will free us from the need to reduce them common one.
. These numbers have the same denominators, and so this will free us from the need to reduce them common one.
First act:
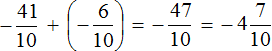
The resulting number can be added to the second summand, which is the rational number 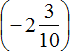 . The rational numbers
. The rational numbers 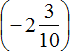 and
and ![]() have the same denominators in the fractional parts, which again is an advantage for us
have the same denominators in the fractional parts, which again is an advantage for us
Second act:
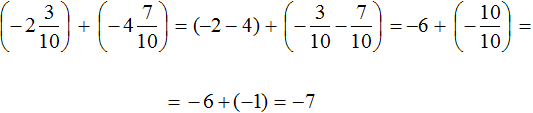
Well, let's add the resulting number ![]() to the last summand, which is the rational number 1/3. Conveniently, when calculating this expression, the sevens will disappear, because their sum will be equal to zero:
to the last summand, which is the rational number 1/3. Conveniently, when calculating this expression, the sevens will disappear, because their sum will be equal to zero:
Third act:
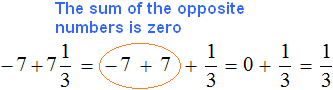
Answer: The value of expression 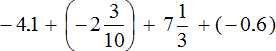 is
is ![]()
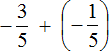
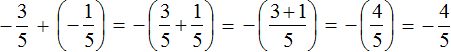
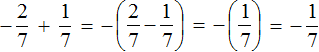
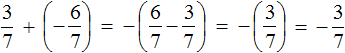
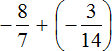
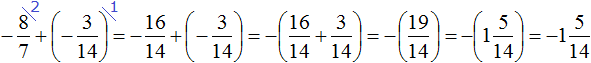
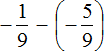
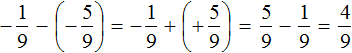
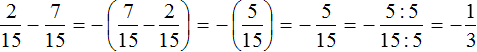
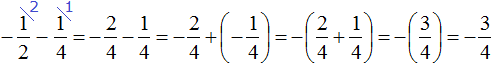
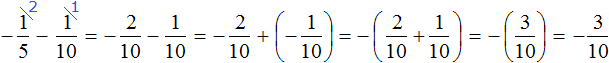
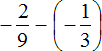
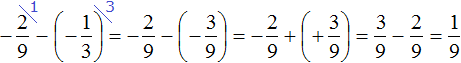
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.