Solving a task with a proportion boils down to making the unknown value of x a member of that proportion. Then using the basic property of the proportion to obtain a linear equation and solve it.
How to solve a task with the help of a proportion
Consider a simple example. Three groups of workers need to be paid wages of $1,600 each. The first group has 20 workers. So the first group will be paid 1600 × 20, or $32,000.
The second group has 17 people. So the second group will be paid 1600 × 17, or $27,200.
So let's pay the third group. There are 15 people in it. We have to pay them 1600 × 15, i.e. $24 thousand.
As a result we have the following solution:
1600 * 20 = $32000
1600 * 20 = $27200
1600 * 20 = $24000
For similar tasks, the solution can be written using a proportion.
Proportion by definition is the equality of two relations. For example, the equality ![]() is a proportion. This proportion can be read as follows:
is a proportion. This proportion can be read as follows:
a relates to b as c relates to d
Similarly, we can relate wages and workers, so that each gets $1,600.
So let's write down the first ratio, which is the ratio of $1,600 per person:
![]()
We find that to pay twenty workers $1,600 each, we would need $32,000. So the second ratio would be the ratio of thirty-two thousand to twenty workers:
![]()
Now connect the obtained relations with an equal sign:
![]()
We got the proportion. It can be read as follows:
$1,600 is as much for one worker as $32,000 is for twenty workers.
That is, $1,600 each. If we divide both parts of Equality ![]() , we find that one worker, as well as twenty workers, will receive $1,600 each.
, we find that one worker, as well as twenty workers, will receive $1,600 each.
Now suppose the amount of money needed to pay the salaries of the twenty workers were unknown. Let's say the question were as follows: there are 20 workers in the group, and each needs to be paid $1,600. How many total dollars are needed to pay the wages?
In this case, the proportion ![]() would take the form
would take the form ![]() . That is, the amount of money needed to pay salaries became an unknown member of the proportion. This proportion can be read as follows:
. That is, the amount of money needed to pay salaries became an unknown member of the proportion. This proportion can be read as follows:
$1,600 is as related to one worker as an unknown number of dollars is to twenty workers
Now let us use the basic property of the proportion. It says that the product of the extreme terms of a proportion is equal to the product of the middle terms:

Multiplying the terms of the proportion "crosswise," we get the equality 1600 × 20 = 1 × x. Calculating both parts of the equality, we get 32000 = x or x = 32000. In other words, we will find the value of the unknown quantity we were looking for.
Similarly, it was possible to determine the total for the remaining number of workers - for 17 and 15. These proportions looked like ![]() and
and ![]() . Using the basic property of the proportion, we can find the value of x
. Using the basic property of the proportion, we can find the value of x
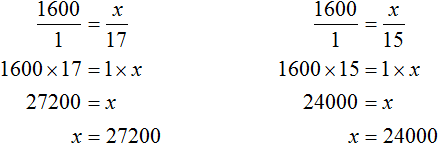
Task 2. The bus traveled a distance of 100 km in 2 hours. How long will it take the bus to travel 300 km at the same speed?
You can first determine the distance the bus travels in one hour. Then determine how many times that distance is contained in 300 kilometers:
100 : 2 = 50 km for each hour of travel
300 km : 50 = 6 hours.
Or you can make the proportion "one hundred kilometers is as related to two hours as three hundred kilometers is to an unknown number of hours."

Ratio of the same-name values
If the extreme or middle terms of the proportion are swapped, the proportion will not be broken.
So, in proportion ![]() you can swap out the outermost terms. Then the proportion is
you can swap out the outermost terms. Then the proportion is ![]() .
.
The proportion will also not be broken if it is reversed, that is, using inverse relations in both parts.
Let's flip the proportion ![]() . Then we get the proportion
. Then we get the proportion ![]() . The relationship is not broken. The ratio between the workers is equal to the ratio between the amounts of money intended for those workers. This proportion is often made at school, when tables are made to solve a task
. The relationship is not broken. The ratio between the workers is equal to the ratio between the amounts of money intended for those workers. This proportion is often made at school, when tables are made to solve a task

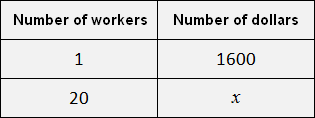
This way of writing is very convenient because it allows you to translate the condition of the task into a more comprehensible form. Let us solve the problem in which we need to determine how many dollars are needed to pay the salaries of twenty workers.
Let us write the condition of the task as follows:
1 worker - $1600
20 workers - x dollars
Let's make a table based on this condition:
Let's make a proportion using the data in the table:
![]()
Using the basic property of the proportion, we obtain a linear equation and find its root:
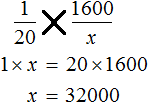
Initially, we dealt with the proportion ![]() , which is made up of ratios of values of different types. In the numerators of the ratio there were amounts of money, and in the denominators there were amounts of workers:
, which is made up of ratios of values of different types. In the numerators of the ratio there were amounts of money, and in the denominators there were amounts of workers:

By interchanging the extreme terms, we get the proportion ![]() . This proportion is made up of ratios of values of the same type. The first ratio contains the number of workers, and the second contains the amount of money:
. This proportion is made up of ratios of values of the same type. The first ratio contains the number of workers, and the second contains the amount of money:
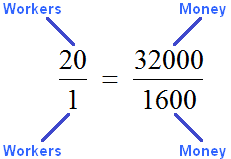
If a relation is composed of quantities of the same type, then we will call it a relation of quantities of the same name. For example, relations between fruits, money, physical quantities, phenomena, and actions.
A relation can be composed of both same-name quantities and quantities of different types. Examples of the latter are the relation of distance to time, the relation of the value of a commodity to its quantity, the relation of the total amount of wages to the number of workers.
Example 2. There are pines and birches planted in the school garden, with two birches for every pine tree. How many pines were planted in the garden if 240 birches were planted?
Determine how many pines were planted in the garden. To do this we make a proportion. The condition says that for every pine there are 2 birches. Write the ratio that shows that there are two birch trees for one pine tree:
![]()
Now write a second ratio showing that there are 240 birches for x pines
![]()
Connect these relations with an equal sign, and we obtain the following proportion:
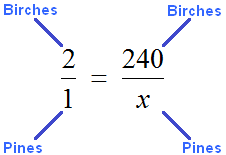
«Two birches are so related to one pine tree,
as 240 birches relate to x pines.»
Using the basic property of the proportion, we find the value of x
![]()
Or the proportion can be made up by writing the condition beforehand, as in the last example:
2 birches - 1 pine tree
240 birches - x pines
You will get the same proportion, but this time it will be made up of ratios of the same names:
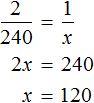
So they planted 120 pine trees in the garden.
Example 3: From 225 kg of ore, 34.2 kg of copper was obtained. What is the percentage of copper in the ore?
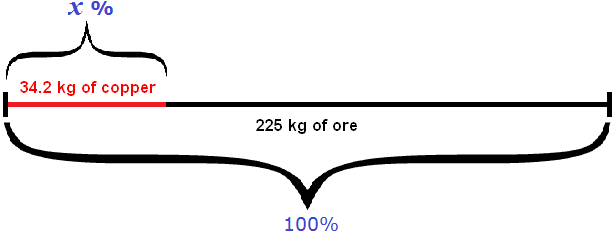
You can divide 34.2 by 225 and express the result as a percentage:
![]()
Or make the proportion 225 kilograms of ore so come to 100%, as 34.2 kg of copper come to an unknown number of percent:

Or make up a proportion in which the relations are composed of the same-name values:
225 kg of ore - 100%
34.2 kg of copper - x%
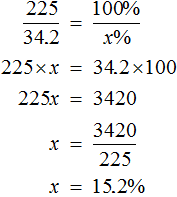
Tasks on direct proportionality
Understanding the relationship between similarly-named quantities leads to an understanding of solving direct and inverse proportionality tasks. Let's start with tasks on direct proportionality.
First, let's remember what direct proportionality is. This is the relationship between two quantities in which an increase in one of them entails an increase in the other by the same factor.
If the bus traveled 50 km in 1 hour, it would take two hours to travel 100 km at the same speed. How many times the distance increased, the same amount of travel time increased. How do you show this with a ratio?
One of the purposes of the ratio is to show how many times the first value is greater than the second value. So we can use the ratio to show that the distance and time have doubled. To do this, use the ratio of the same values.
Let's show that the distance doubled:
![]()
Similarly, let's show that the time has increased by the same factor
![]()
Let's connect these relations with an equal sign, and get a proportion:
![]()
«100 kilometers relates to 50 kilometers the way 2 hours relate to 1 hour»
If we divide both parts of Equality ![]() , we find that distance and time have been increased by the same number of times.
, we find that distance and time have been increased by the same number of times.
2 = 2
Task 2: The mill milled 27 tons of wheat flour in 3 hours. How many tons of wheat flour can be ground in 9 hours if the rate of work does not change?
Solution
The working time of the mill and the weight of the ground flour are directly proportional quantities. If you increase the working time by a factor of two the amount of flour ground will increase by the same factor. Let's show it with the help of a proportion.
The task is given as 3 h. Those 3 hrs increased to 9 hrs. Let's write down the ratio of 9 hours to 3 hours. This ratio will show how many times the time the mill worked has increased:
![]()
Now write down the second ratio. This will be the ratio of x tons of wheat flour to 27 tons. This ratio will show that the amount of milled flour has increased by the same factor as the operating time of the mill
![]()
Connect these relations with an equal sign, and we obtain the proportion ![]() .
.
Let's use the basic property of the proportion and find x
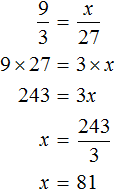
So 81 tons of wheat flour can be milled in 9 hours.
In general, if you take two directly proportional quantities and increase them by the same number of times, then the ratio of the new value to the old value of the first quantity will be equal to the ratio of the new value to the old value of the second quantity.
So in the previous problem, the old values were 3 h and 27 t. These values were increased by the same number of times (three times). The new values are 9 h and 81 h. Then the ratio of the new mill running time to the old value of ![]() is equal to the ratio of the new value of the mass of the ground flour to the old value of
is equal to the ratio of the new value of the mass of the ground flour to the old value of ![]()
![]()
If we divide both parts of the equality, we find that the time of the mill and the amount of flour milled increased by the same number of times:
3 = 3
The proportion, which is made to the tasks on direct proportionality, can be described with the help of the expression:
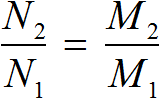
| Where | |
For our task, the values of the ![]()
![]()
![]()
![]() variables will be as follows:
variables will be as follows:
Where ![]() subsequently became 81.
subsequently became 81.
Task 2. For 8 cows in winter time a dairymaid procures 80 kg of hay, 96 kg of root vegetables, 120 kg of silage, and 12 kg of concentrates daily. Determine the daily consumption of these feeds for 18 cows.
Solution
The number of cows and the mass of each feed are directly proportional quantities. If you increase the number of cows by several times, the mass of each of the feeds will increase by the same number of times.
Let's make some proportions that calculate the mass of each feed for 18 cows.
Let's start with hay. Each day for 8 cows, 80 kg of hay is prepared. Then x kilograms of hay will be prepared for 18 cows.
Let's write down the ratio showing how many times the number of cows increased:
![]()
Now let's write down the ratio that shows how many times the mass of hay increased:
![]()
Let's connect these relations with an equal sign, and get a proportion:
![]()
From this we find x
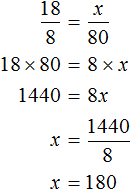
So for 18 cows we need to prepare 180 kg of hay. Similarly determine the mass of root crops, silage and concentrates.
For 8 cows 96 kg of root crops are harvested daily. Then for 18 cows x kg of root crops will be harvested. Make a ratio of ![]() and
and ![]() , then calculate the value of x
, then calculate the value of x
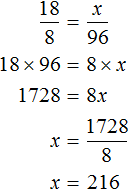
Let's determine how much silage and concentrates we need to prepare for 18 cows:
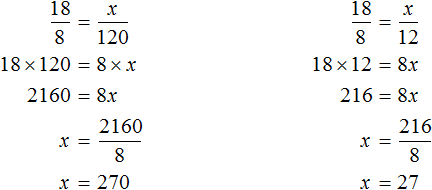
So for 18 cows you need to prepare 180 kg of hay, 216 kg of root vegetables, 270 kg of silage and 27 kg of concentrates daily.
Task 3. The hostess makes cherry jam, and for 3 cups of cherries she puts 2 cups of sugar. How much sugar should be put on 12 cups of cherries? on 10 cups of cherries? on ![]() cups of cherries?
cups of cherries?
Solution
The number of cups of cherries and the number of cups of sugar are directly proportional quantities. If we increase the number of glasses of cherries by several times, the number of glasses of sugar will increase by the same number of times.
Let's write down the ratio showing how many times the number of glasses of cherries increased:
![]()
Now write down the ratio showing how many times the number of cups of sugar increased:
![]()
Let's connect these relations with an equal sign, get the proportion and find the value of x
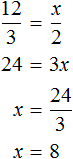
So for 12 cups of cherries you need to put 8 cups of sugar.
Determine the number of cups of sugar for 10 cups of cherries and ![]() cups of cherries
cups of cherries

Inverse Proportion Tasks
Again, to solve problems on inverse proportionality, you can use a proportion made up of ratios of the same-name quantities.
Unlike direct proportionality, where quantities increase or decrease in the same direction, in inverse proportionality quantities change inversely to each other.
If one quantity increases several times, the other quantity decreases by the same factor. And vice versa, if one quantity decreases several times, the other quantity increases as much.
Suppose you want to paint a fence consisting of 8 sheets of

One painter will paint all 8 sheets himself
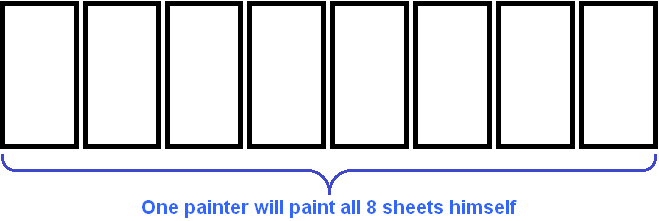
If there are two painters, each will paint four sheets.
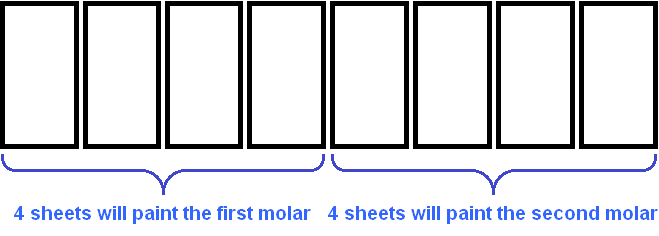
This is assuming, of course, that the painters are honest with each other and fairly divide the work equally between them.
If there are four painters, each will paint two sheets.
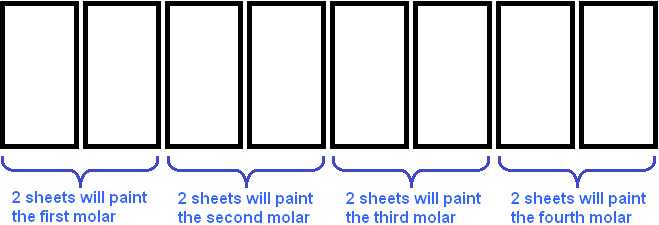
Note that if we increase the number of painters by several times, the number of sheets that come to one painter decreases by the same factor.
So, we increased the number of painters from 1 to 4. In other words, we increased the number of painters by a factor of four. Let's write it down using a ratio:
![]()
As a result, the number of fence sheets per painter has decreased by a factor of four. Let's write it down using a ratio:
![]()
Connect these relations with an equal sign, and we obtain the proportion
![]()
«4 painters refer to 1 painter as 8 sheets refer to 2 sheets»
Task 2. 15 workers finished finishing the apartments in a new house in 24 days. How many days would it take 18 workers to complete the job?
Solution
The number of workers and the number of days spent on the job are inversely proportional quantities. If you increase the number of workers by several times, the number of days it would take to do the job would decrease by the same factor.
Let's write down the ratio of 18 workers to 15 workers. This ratio will show how many times the number of workers increased
![]()
Now write the second ratio showing how many times the number of days decreased. Since the number of days will decrease from 24 days to x days, the second ratio is the ratio of the old number of days (24 days) to the new number of days (x days)
![]()
Connect the obtained relations with an equal sign, and we obtain a proportion:
![]()
From this we find x
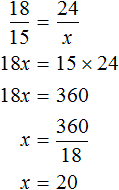
So 18 workers will do the necessary work in 20 days.
In general, if you take two inverse proportional quantities and increase one of them by a certain number of times, then the other will decrease by the same number of times. Then the ratio of the new value to the old value of the first value will be equal to the ratio of the old value to the new value of the second value.
So in the previous problem the old values were 15 workers and 24 days. The number of workers was increased from 15 to 18 (i.e., was increased by a factor of ![]() ). As a result, the number of days needed to do the work decreased by the same factor. The new values were 18 workers and 20 days. Then the ratio of the new number of workers to the old number of
). As a result, the number of days needed to do the work decreased by the same factor. The new values were 18 workers and 20 days. Then the ratio of the new number of workers to the old number of ![]() equals the ratio of the old number of days to the new number of
equals the ratio of the old number of days to the new number of ![]()
You can use the formula to make the ratio for inverse proportionality tasks:
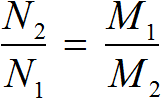
| Where | |
Where ![]() subsequently became 20.
subsequently became 20.
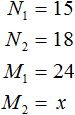
Task 2. The speed of the steamboat refers to the speed of the river flow as 36 : 5. The steamboat traveled downstream for 5 hours and 10 minutes. How long will it take him to get back?
Solution
The actual speed of the steamboat is 36 km/h. The speed of the river current is 5 km/h. Since the steamboat moved along the stream of the river, its speed was 36 + 5 = 41 km/h. The travel time was 5 h 10 min. For convenience, let us express the time in minutes:
5 h 10 min = 300 min + 10 min = 310 min
Since the steamboat moved against the flow of the river on the way back, its speed was 36 - 5 = 31 km/h.
The speed of the steamboat and the time of its motion are inversely proportional quantities. If her speed decreases by several times, her travel time will increase by the same number of times.
Write down the ratio showing how many times the speed decreased:
![]()
Now write down the second ratio showing by how many times the movement time has increased. Since the new time x will be greater than the old time, write time x in the numerator and the old time equal to three hundred and ten minutes in the denominator
![]()
Let's connect these relations with an equal sign to get the proportion ![]() . From here we find the value of x
. From here we find the value of x
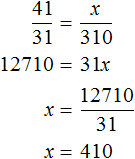
410 minutes is 6 hours and 50 minutes. So it will take the steamer 6 hours and 50 minutes to get back.
Task 3. 15 people were working on the road repair, and they were supposed to finish the work in 12 days. On the fifth day, some more workers arrived in the morning, and the remaining work was done in 6 days. How many additional workers arrived?
Solution
Let's subtract 4 days worked from the 12 days. This will determine how many more days the fifteen workers have left to work
12 days - 4 days = 8 days.
On the fifth day x more workers arrived. Then the total number of workers is 15 + x.
The number of workers and the number of days needed to do the work are inversely proportional values. If you increase the number of workers by several times, then the number of days will be reduced by the same factor.
Let's write down the ratio showing how many times the number of workers increased:
![]()
Now write down by how many times the number of days needed to do the work has decreased:
![]()
Connect these relations with an equal sign, and you get the proportion ![]() . From this we can calculate the value of x
. From this we can calculate the value of x
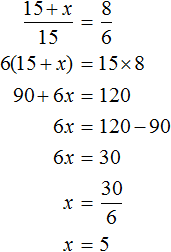
So five additional workers arrived.
The scale
Scale is the ratio of the length of the segment in the image to the length of the corresponding segment on the ground.
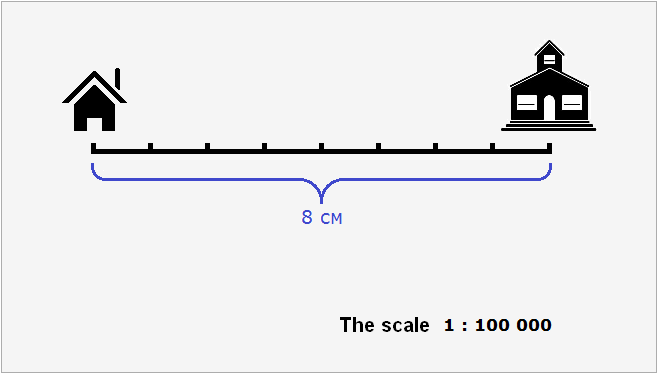
Suppose the distance from the house to the school is 8 km. Let's try to draw a plan of the area with the house, the school, and the distance between them. But we cannot represent on paper the distance equal to 8 km, because it is quite large. But we can reduce this distance several times so that it fits on the paper.
Let the kilometers on the ground on our plan be expressed in centimeters. If we convert 8 kilometers to centimeters, we get 800,000 centimeters.
Reduce 800,000 cm by a hundred thousand times:
800,000 cm : 100,000 cm = 8 cm.
8 cm is the distance from the house to the school, reduced a hundred thousand times. Now you can easily draw a house and a school on paper with a distance of 8 cm between them.
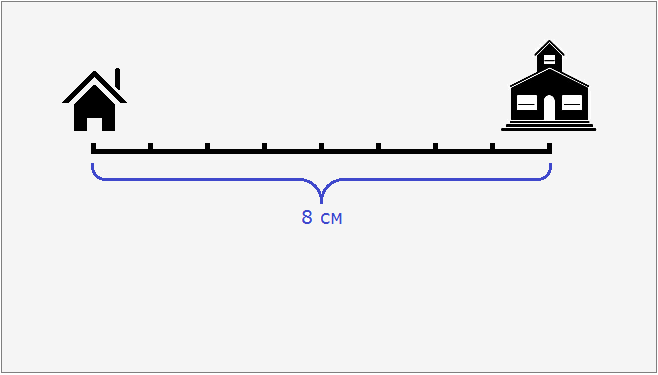
These 8 cm refer to the real 800,000 cm. So let's write it down using the ratio:
8 : 800 000
One of the properties of the ratio says that the ratio does not change if its terms are multiplied or divided by the same number.
To simplify the relation 8 : 800 000, both of its terms can be divided by 8. Then we obtain the ratio 1 : 100 000. We will call this ratio the scale. This ratio shows that one centimeter on the plan refers to (or corresponds to) a hundred thousand centimeters on the ground.
Therefore, in our figure, we need to indicate that the plan is drawn at a scale of 1 : 100 000
Examples:
1 cm on the plan refers to 100,000 cm on the ground;
2 cm on the plan refers to 200000 cm on the ground;
3 cm on the plan refers to 300,000 cm on the ground, etc.
Any map or plan is indicated at what scale they were made. This scale allows you to determine the actual distance between objects.
So, our plan is drawn at a scale of 1 : 100,000. On this plan, the distance between the house and the school is 8 cm. To calculate the real distance between the house and the school, you need to multiply 8 cm by 100,000 times. In other words, multiply 8 cm by 100,000.
8 cm × 100,000 = 800,000 cm.
We get 800,000 cm, or 8 km if you convert centimeters to kilometers.
Suppose there is a tree between the house and the school. On the plan, the distance between the school and this tree is 4 cm.
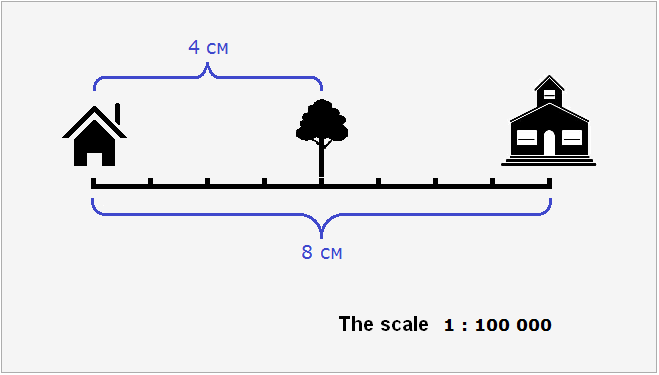
Then the actual distance between the house and the tree would be 4 cm × 100,000 = 400,000 cm or 4 km.
The distance on the ground can be determined by using a proportion. In our example, the distance between the house and the school will be calculated using the following proportion:
![]()
This proportion can be read as follows:
1 cm on the plan refers to 100000 cm on the ground, as 8 cm on the plan refers to x cm on the ground.
From this proportion we learn that the value of x is 800000 cm.
Example 2. On the map the distance between two cities is 8.5 cm. Determine the real distance between the cities, if the map is drawn at a scale of 1 : 1 000 000.
Solution
The scale 1 : 1,000,000 indicates that 1 cm on the map corresponds to 1,000,000 cm on the ground. Then 8.5 cm would correspond to x cm on the ground. Make the proportion 1 to 1000000 as 8.5 to x
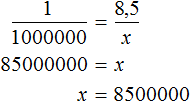
1 km contains 100,000 cm. Then 8,500,000 / 100,000 cm would be 85 km
Or we can reason this way. The distance on the map and the distance on the ground are directly proportional quantities. If you increase the distance on the map by several times, the distance on the ground will increase by the same number of times. Then the proportion will take the following form. The first ratio will show how many times the distance on the ground is greater than the distance on the map:
![]()
The second ratio will show that the distance on the ground is as many times greater than the 8.5 cm on the map:
![]()
Hence x equals 8,500,000 cm or 85 km.

Task 3. The length of the river is 74 km. What is its length on the map, which scale is 1 : 2 000 000
Solution
The scale 1 : 2000000 shows that 1 cm on the map corresponds to 2 000 000 cm on the ground.
And 74 km is 74 × 100,000 = 7,400,000 cm on the ground. By reducing 7,400,000 to 2,000,000, we determine the length of the river on the map
7,400,000 : 2,000,000 = 3.7 cm
So on a map whose scale is 1 : 2,000,000, the length of the river is 3.7 cm.
Let's write down the solution using a ratio. The first ratio will show how many times the length on the map is less than the length on the ground:
![]()
The second ratio would show that 74 km (7,400,000 cm) decreased by the same factor:
![]()
From this we find x equals 3.7 cm

Tasks for independent decision
Solution
Let x kg of oil be obtained from 7 kg of cotton seed. The mass of the cotton seed and the mass of the resulting oil are directly proportional quantities. Then the reduction of the cotton seed from 21 kg to 7 kg, will lead to a reduction of the received oil by the same factor.
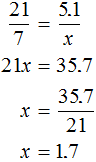
Answer: 7 kg of cotton seed will yield 1.7 kg of oil.
Solution
The length of the section on which the rails are replaced is 8 × 360 = 2880 m.
Let x twelve-meter rails be required for replacement. Increasing the length of one rail from 8 m to 12 m will reduce the number of rails from 360 to x pieces. In other words, the rail length and the number of rails are related by an inverse relation
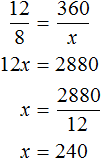
Answer: 240 new rails will be needed to replace the old ones.
Solution
If 60% of the students went to the movies and the other 12 went to the exhibition, then 40% of the students will account for the 12 students who went to the exhibition. Then we can make a proportion in which the 12 students are related to 40% the way all x students are related to 100%
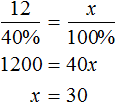
Or you can make a proportion consisting of ratios of the same names. The number of students and the percentage change in direct proportion. Then we can write that the number of participants ![]() increases as much as the percentage of
increases as much as the percentage of ![]() increases (from 40% to 100%)
increases (from 40% to 100%)
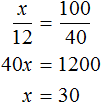
Answer: there are 30 students in the class.
Solution
The scale of 1 : 500,000 tells us that 1 cm on the map corresponds to 500,000 cm on the ground.
Then magnifying 18 cm into 500,000, we get the actual distance between the cities
18 cm × 500,000 = 9,000,000 cm
Let's convert 9,000,000 cm to kilometers. There are 100,000 cm in one kilometer. Then 9,000,000 cm would be 9,000,000 / 100,000 = 90 km
Let's write down the solution using the proportion:
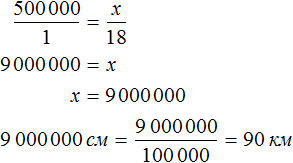
Answer: The distance between the cities is 90 km.
Solution
Speed and time are inversely proportional quantities. If you increase the speed by several times, the travel time will decrease by the same number of times.
Let's write down the ratio showing how many times the pedestrian's speed has increased:
![]()
Let's write down the ratio showing that the time of motion has decreased by the same factor:
![]()
Let's connect these relations with an equal sign, get the proportion and find the value of x
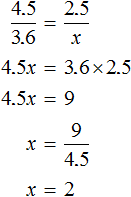
Answer: the walker will take 2 hours if he moves at a speed of 4.5 km/h.
Solution
The expression "exceeded the plan by 15%" means that on top of the existing 100% plan they fulfilled another 15% of the same plan. In total, 115% of the plan was fulfilled. These 115% are accounted for by 230 machines produced
![]()
And the plan was to produce x machines. These x machines account for 100% of the original plan
![]()
Make a proportion of the available relations and find the value of x
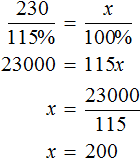
Or you can use the ratios of the values of the same name. The number of machines produced and the percentage of machines produced are related in a directly proportional way. If the number of machines is increased by a factor of several, the percentage increases by the same factor. Then we can write that 230 machines is as many times as x machines as 115% as 100%
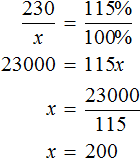
Answer: The plan was for the plant to produce 200 machines.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.