This lesson will be interesting and informative. We will learn how to apply fractions to a variety of life situations.
How to find a fraction of a whole number
We already said that a fraction is a part of something. That part can be anything. For example, 
of a pizza is a half of a pizza:
But the usage of fractions does not end with one pizza. For example, you can find out how much is of ten centimeters:
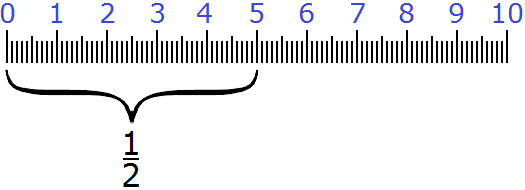
As you have already guessed, of ten centimeters is five centimeters. After all, is the simplest fraction, which means half of something. We had ten centimeters. We divided those ten centimeters in half and got five centimeters.
Let's try to find out how much is of one hour. Recall that an hour is 60 minutes. We need to find (half) of 60 minutes. It is not difficult to guess that half of 60 minutes is 30 minutes. So of one hour is 30 minutes or half an hour.
Let's try to find of one centner. A centner is 100 kg. We need to find (half) of 100 kg. It is easy to guess that half of 100 kg is 50 kg. So of one centner is 50 kg.
Since we are doing math, it means that in most cases we will be dealing with numbers. For example, let's find from the number 12.
So, we need to find half of the number 12. It is not difficult to guess that half of number 12 is number 6. So of 12 is 6.
To make it easier to find a fraction from a number, you can use the following rule:
To find a fraction of a number, divide the number by the denominator of the fraction, and multiply the result by the numerator of the fraction.
Let's try to trace the entire process of this rule. Let's take ten centimeters as an example:
Let it be required to find of those ten centimeters. Read the first part of the rule:
To find a fraction of a number, divide the number by the denominator of the fraction
So, we divide ten centimeters by the denominator of the fraction . The denominator of this fraction is 2. Therefore, we divide ten centimeters by 2
10 cm : 2 = 5 cm
Read the second part of the rule:
and multiply the result by the numerator of the fraction
So we multiply five centimeters by the numerator of the fraction . The numerator of the fraction in this case is one. Therefore multiply five centimeters by one:
5 cm × 1 = 5 cm
We found of ten centimeters. We see that of ten centimeters is five centimeters:
Why do we have to multiply the result by the numerator after dividing a number by the denominator of a fraction? The fact is that the denominator of a fraction shows how many parts something is divided into, and the numerator shows how many parts were taken.
In our example, the ten centimeters were divided into two parts (in half), and one part was taken from those parts. By multiplying one part by the numerator of a fraction, we are indicating how many parts we are taking from something. That is, by multiplying five centimeters by the numerator of the fraction , we indicated that we were taking one part of two.
Example 2. Find 
of 10 cm.
Apply the rule of finding fractions from a number:
To find a fraction of a number, divide the number by the denominator of the fraction, and multiply the result by the numerator of the fraction.
First, we divide 10 centimeters by the denominator of the fraction
10 cm : 5 = 2 cm
You got two centimeters. This result should be multiplied by the numerator of the fraction
2 cm × 2 = 4 cm
We found of ten centimeters. We see that of ten centimeters is four centimeters.
The entire solution process can be seen in the following figure:
First, the ten centimeters were divided into five equal parts. Then two parts of those five parts were taken:
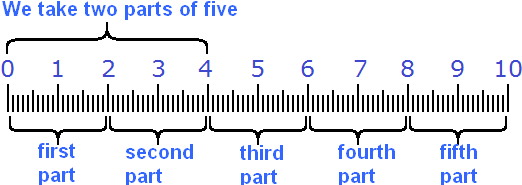
Example 3. Find 
of the number 56.
To find 
of 56, divide the number by the denominator of the fraction , and multiply the result by the numerator of the fraction .
So, first, we divide the number 56 by the denominator of the fraction
56 : 8 = 7
Now multiply the result by the numerator of the fraction
7 × 3 = 21
The answer is 21. So of 56 is 21.
Example 4. Find 
of one hour.
One hour is 60 minutes. The assignment can be understood as finding of 60 minutes.
First divide 60 minutes by the denominator of the fraction
60 min : 4 = 15 min
Now multiply the 15 minutes by the numerator of the fraction
15 min × 2 = 30 min
The answer is 30 minutes. So of one hour is thirty minutes or half an hour.
Example 5. Find 
of one meter.
One meter is one hundred centimeters. First divide 100 cm by the denominator of the fraction
100 cm : 5 = 20 cm
Now multiply the resulting 20 cm by the numerator of the fraction
20 cm × 4 = 80 cm
The answer is 80 cm. So of one meter is 80 cm.
Finding a whole number when a fraction is known
Knowing part of a number and how much of it is from a whole number, you can find the original whole number. This is the inverse of the problem we looked at in the previous topic. There, we searched for the fraction of a number by dividing the number by the denominator of the fraction, and multiplying the result by the numerator of the fraction.
Now, on the contrary, knowing the fraction and how much it is of the number, we need to find the original whole number.
For example, if of the length of a ruler is six centimeters and we are told to find the length of the entire ruler, we should understand that we are required to find the original whole (the length of the entire ruler) by the fraction . Let's solve this problem.
Find the length of the whole ruler by the fraction . It is known that of the length of the whole ruler is 6 cm.
We already know how we got the 6 cm. There was some length, and it was divided into five parts, because the denominator of the fraction is the number 5. Then two parts of the five parts were taken because the numerator of the fraction is number 2.
To know the length of the whole ruler, you first need to know the length of one part. How do we find this out? Let's try to guess by looking closely at the following picture:
If two parts of the length of the ruler are 6 cm, then it is easy to guess that one part is 3 cm. And to get those 3 cm, you have to divide 6 by 2.
6 cm : 2 = 3 cm
So we found the length of one part. One part of five, or 
of the length of a ruler, is 3 cm. If there are only five parts, then to find the length of the ruler, you have to take three centimeters five times. In other words, multiply 3 cm by the number 5
3 cm × 5 = 15
We found the length of the ruler. It is 15 centimeters. This can be seen in the following picture.
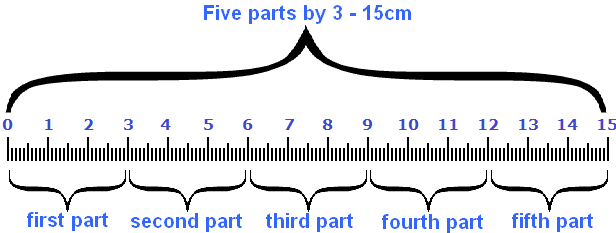
You can see that five parts of five or 
make fifteen centimeters.
To make it easier to find a number by its fraction, you can use the following rule:
To find a number by its fraction, you need to divide the known number by the numerator of the fraction, and multiply the result by the denominator of the fraction.
Example 2. The number 20 is of the whole number. Find this number.
The denominator of the fraction shows that the number we need to find is divided into five parts. If of that number is 20, then to find the whole number, we must first find (one part of five) of the whole number. To do this, 20 must be divided by the numerator of the fraction
20 : 4 = 5
We found of the whole number. That fraction is 5. To find the whole number, multiply the result of 5 by the denominator of the fraction
5 × 5 = 25
We found of the whole number. In other words, we found the whole number we were asked to find. That number is 25.
Example 3. Ten minutes is 
of the cooking time of the porridge. Find the total cooking time of the porridge.
The denominator of the fraction shows that the total cooking time of the porridge is divided into three parts. If of the cooking time is ten minutes, then to find the total cooking time, you must first find 
of the cooking time. To do this, divide 10 by the numerator of fraction
10 min : 2 = 5 min
We found of the porridge cooking time. of the porridge cooking time is five minutes. To find the total cooking time, multiply 5 minutes by the denominator of the fraction 
5 min × 3 = 15 min
We found 
of the cooking time of the porridge, that is, we found the total cooking time. It is 15 minutes.
Example 4. 
of the mass of a sack of cement is 30 kg. Find the total mass of the sack.
The denominator of the fraction shows that the total mass of the sack is divided into four parts. If the mass of the sack is 30 kg, then in order to find the total mass of the sack you must first find 
of the mass of the sack. To do this, divide 30 by the numerator of the fraction .
30kg : 2 = 15kg
We found of the mass of the sack. The mass of the sack is 15 kg. Now to find the total mass of the sack, multiply 15kg by the denominator of the fraction
15kg × 4 = 60kg
We found the 
mass of the sack. In other words, we found the total mass of the sack. The total mass of the sack of cement is 60 kg.
Dividing a smaller number by a larger number
Situations often arise in life when you need to divide a smaller number by a larger one. For example, imagine a situation. There are three friends:
And you need to divide the two apples equally between them. How to do this? There are three friends and only two apples. We find ourselves in a situation where we need to divide a smaller number by a larger one (two apples for three).
The following rule is provided for such cases:
Dividing a smaller number by a larger number produces a fraction with the smaller-one divisor in the numerator and the bigger-one divisor in the denominator.
Let's apply this rule. It says that dividing a smaller number by a larger number produces a fraction with the numerator being the divisor and the denominator being the divisor. The divisor is two apples. Write the number 2 in the numerator:
And the divisor is the three friends (remember, the divisor shows how many parts we need to divide the divisor into). Write the three in the denominator of our fraction:
It's funny, but a fraction of 
is the answer to our problem. Each friend gets of an apple. Why did this happen?
To divide two apples among three people, you must cut each apple with a knife into three pieces and distribute these pieces equally among the three friends:
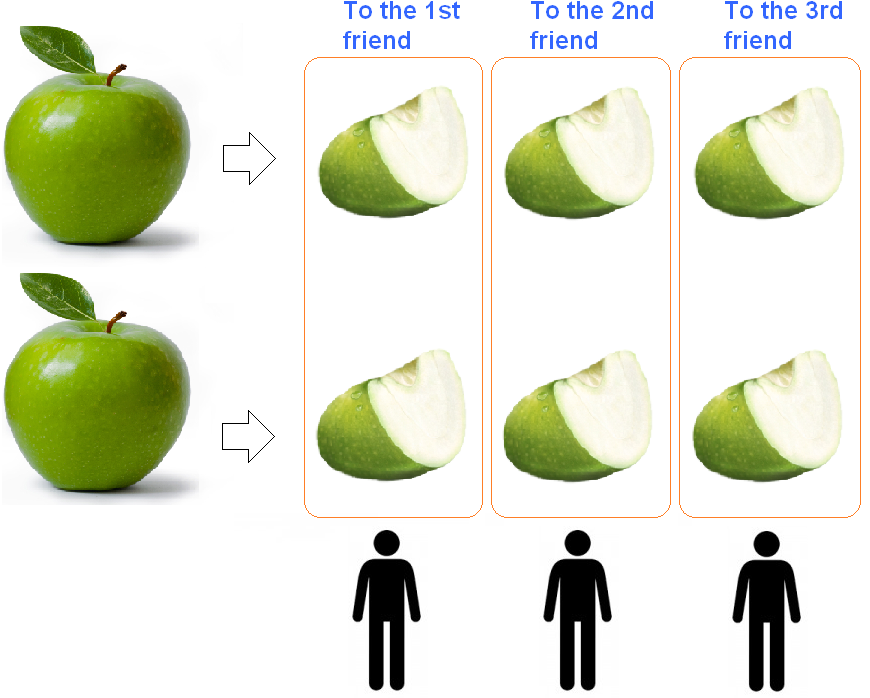
As you can see in the picture, each apple was divided into three pieces and scattered equally among the three friends. Each friend got of an apple (two slices out of three).
Ratio Between Two Numbers
Sometimes it is necessary to find out what part of the first number makes up the second. The following rule is provided for such cases:
To find out what is the ratio between two numbers, you need to divide the first number by the second.
For example, an apple is divided into five identical slices. How much of the apple are the two slices?
To answer this question, you must divide the first number by the second. The first number is 2 and the second is 5. You get a fraction 
.
So two slices out of five slices make up two fifths. This can be seen in the following picture:
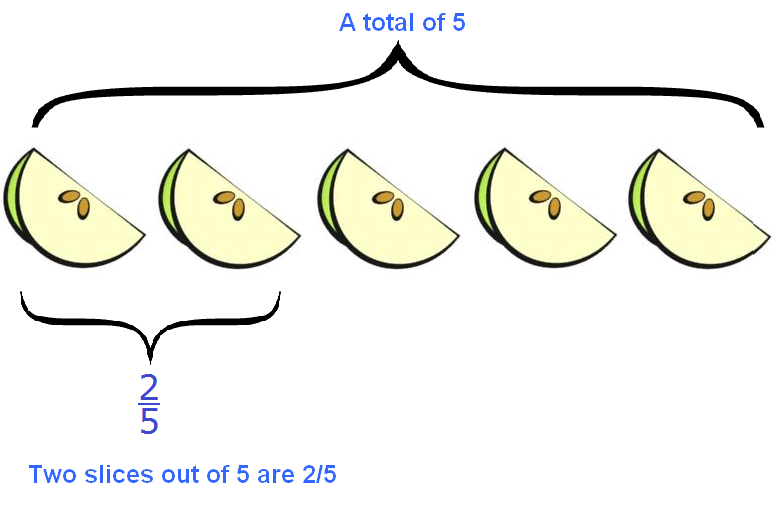
So, two apple slices out of five make two fifths.
The question arises, but how do you know which number is the first and which is the second? To do this, look at the question in the problem. The number in the question will be the first number. For example, in the previous problem the question was put like this:
"How much of an apple is made up of two slices like this?"
If you look closely at the question, you will find that there is a number 2. That was the first number.
Sometimes there are two numbers in the question. For example: What part of the number 2 is 10?
In this case, the first number will be the one in the question before. In this case, the first number is 2 and the second is 10. Dividing 2 by 10, we get a fraction 
. So the number 2 of 10 is (two tenths).
The fraction means that the number 10 is divided into ten parts, and two parts are taken from those ten parts.
Also, this fraction can be reduced by 2. After reducing the fraction by 2, we get the fraction 
.
The fraction can also serve as an answer to the problem. It would mean that the number 10 is divided into five parts, and one part is taken from those five parts.
Thus, number 2 is (one fifth) of number 10.
Example 3. Whats the ratio between 5 and 15?
Divide the first number by the second. The first number is 5 and the second is 15. Dividing 5 by 15, we get a fraction 
. This fraction can be reduced by 5
We got a neat fraction of 
. So the answer will look like this:
The number 5 is (one third) of the number 15.
This can even be checked. To do this, we need to find of the number 15. If we have done everything correctly, we should get the number 5.
So let's find of a number 15. We already know how to find a fraction from a number
15 : 3 = 5
5 × 1 = 5
You got the answer 5. So the problem was solved correctly.
Example 4. What ratio between 3 cm and 12 cm?
Divide the first number by the second. The first number is 3 and the second is 12. We get a fraction 
. This fraction can be reduced by 3
The answer is 
. So 3 cm is (one fourth) of 12 cm.
Let's check if we solved this problem correctly. To do this, find of 12 cm. If we did everything correctly, we should get 3 cm.
Divide 12 by the denominator of the fraction
12 cm : 4 = 3 cm
Multiply 3 cm by the numerator of the fraction
3 cm × 1 = 3 cm
The answer is 3 cm. So the problem was solved correctly.
Exercises
of the number 48. of this number is 16.8 × 3 = 24
of this number is 32.32 × 2 = 64
of this number is 150.30 × 8 = 240
of the path is 4 km.2 km × 3 = 6 km
of it is 100 cm.20 cm × 8 = 160 cm
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.