It often happens that we have to compare fractions with different numerators and different denominators.
For example, compare fractions 
and 
. To answer the question of which of these fractions is larger or smaller, you must reduce them to the same (common) denominator. Then you can easily determine which fraction is larger or smaller.
Let's reduce fractions and to the same (common) denominator. Find the least common multiple (LCM) of the denominators of both fractions. The LCM of the denominators of fractions and is 6.
Now find the additional multipliers for each fraction. Divide the LCM by the denominator of the first fraction . LCM is 6, and the denominator of the first fraction is 2. Divide 6 by 2, and we get an additional factor 3. Write it over the first fraction:
Now find the second additional factor. Divide the LCM by the denominator of the second fraction . LCM is 6, and the denominator of the second fraction is 3. Dividing 6 by 3, we get an additional multiplier of 2. Write it over the second fraction:
Multiply the fractions by their additional multipliers:
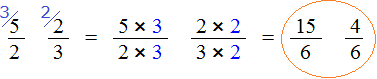
We came to the conclusion that fractions with different denominators turned into fractions with the same denominators. And we already know how to compare such fractions. Of two fractions with the same denominators, the one with the larger numerator is larger:
The rule is a rule, but we'll try to figure out why 
is bigger than 
. To do this, we highlight the whole part in the fraction . In the fraction , we don't need to isolate anything, because the fraction is proper.
After singling out the whole part of the fraction , we obtain the following expression:
After isolating the whole part in the fraction , we get the following expression:
Now it's easy to see why is bigger than . Let's draw these fractions as pizzas:
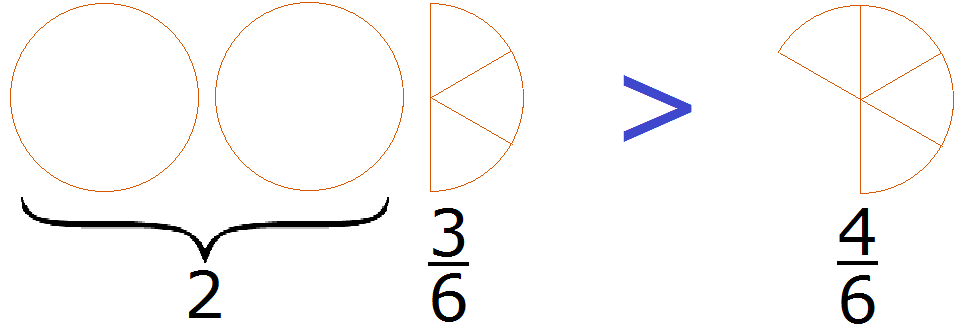
2 whole pizzas and 
pizzas, more than pizzas.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.