Equations are one of the hardest topics to learn, yet they are a powerful enough tool to solve most problems.
Equations are used to describe various processes that occur in nature. Equations are widely used in other sciences: economics, physics, biology, and chemistry.
In this lesson, we will try to understand simple equations, learn how to express the unknowns, and solve several equations. As we learn new material, the equations will become more complex, so understanding the basics is very important.
What is an equation?
The equation contains a variable whose value you want to find. This value must be such that when substituted into the original equation, it results in a valid numerical equality.
For example, the expression 3 + 2 = 5 is an equality. Calculating the left side, the numerical equality 5 = 5 is true.
But the equation 3 + x = 5 contains a variable x, the value of which can be found. The value must be such that when you substitute this value into the original equation, you get the correct numerical equation.
In other words, we must find a value where the equal sign justifies its location-the left side must be equal to the right side.
The equation 3 + x = 5 is elementary. The value of the variable x equals number 2. For any other value the equality will not hold
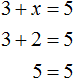
The number 2 is said to be the root or solution of the equation 3 + x = 5
The root or solution to an equation is the value of the variable at which the equation converts to a valid numerical equation.
There may be several roots or no roots at all. Solving an equation means finding its roots or proving that there are no roots.
The variable in the equation is otherwise called the unknown. You are free to call it whatever you like. These are synonyms.
Note. The phrase "solve an equation" speaks for itself. To solve an equation means to "equalize" an equality - to make it balanced so that the left side equals the right side.
Express one through the other
The study of equations traditionally begins with learning to express one number in an equation through a series of others. Let us not break this tradition and do the same.
Consider the following expression:
8 + 2
This expression is the sum of the numbers 8 and 2. The value of this expression is 10
8 + 2 = 10
You have obtained the equality. Now you can express any number from this equality through other numbers in the same equality. For example, express the number 2.
To express the number 2, you need to ask the question: "What should be done with the numbers 10 and 8 to get the number 2?". It is clear that in order to get the number 2, you need to subtract number 8 from the number 10.
And so we do. Write the number 2 and through the equals sign, saying that in order to get the number 2 we subtracted from the number 10 the number 8:
2 = 10 − 8
We expressed the number 2 from the equality 8 + 2 = 10. As you can see from the example, there is nothing complicated about this.
When solving equations, particularly when expressing one number through another, it is convenient to replace the equal sign with the word "is". This should be done mentally, not in the expression itself.
For example, expressing the number 2 from the equation 8 + 2 = 10, we got the equation 2 = 10 - 8. This equality can be read as follows:
2 is 10 - 8
That is, the sign = is replaced by the word "is". Moreover, the equality 2 = 10 - 8 can be translated from mathematical language to full human language. Then it can be read as follows:
The number 2 is the difference of the number 10 and the number 8
or
The number 2 is the difference between the number 10 and the number 8.
But we will limit ourselves to replacing the equal sign with the word "is," and we will not always do so. Elementary expressions can be understood without translating mathematical language into human language.
Let's return the resulting equality 2 = 10 - 8 to its original state:
8 + 2 = 10
This time we express the number 8. What do we do with the other numbers to get the number 8? That's right, subtract the number 2 from the number 10.
8 = 10 − 2
Let us return the resulting equality 8 = 10 - 2 to its original state:
8 + 2 = 10
This time we express the number 10. But it turns out that we don't need to express the ten because it is already expressed. It is enough to swap the left and the right parts, and then we get what we need:
10 = 8 + 2
Example 2. Consider the equality 8 - 2 = 6
Express the number 8 from this equation. To express the number 8, add the other two numbers:
8 = 6 + 2
Let's return the resulting equality 8 = 6 + 2 to its original state:
8 − 2 = 6
Express the number 2 from this equation. To express the number 2, subtract 6 from 8.
2 = 8 − 6
Example 3. Consider the equality 3 × 2 = 6
Let's express the number 3. To express 3, divide 6 by 2
Let's return the resulting equality to its original state:
3 × 2 = 6
Let's express the number 2 from this equality. To express the number 2, you need to divide 6 by 3
Example 4. Consider the equality 
Let's express the number 15 from this equation. To express 15, multiply 3 and 5
15 = 3 × 5
Let's return the resulting equality 15 = 3 × 5 to its original state:
Express the number 5 from this equation. To express the number 5, divide 15 by 3
Rules for finding the unknowns
Consider a few rules for finding the unknowns. You may be familiar with them, but it doesn't hurt to repeat them again. In the future, you can forget them because we will learn to solve equations without applying these rules.
Let's go back to the first example we looked at in the previous topic, where we needed to express the number 2 in the equality 8 + 2 = 10.
In the equality 8 + 2 = 10, the numbers 8 and 2 are terms and the number 10 is the sum.
To express the number 2, we did the following:
2 = 10 − 8
That is, we subtracted the term 8 from the sum of 10.
Now imagine that in the equality 8 + 2 = 10 instead of number 2 there is a variable x
8 + x = 10
In this case, the equality 8 + 2 = 10 turns into the equation 8 + x = 10, and the variable x is the unknown summand
Our task is to find this unknown, that is, to solve the equation 8 + x = 10. The following rule is provided for finding the unknown:
To find an unknown term, subtract a known term from the sum.
That's what we did when we expressed the 2 in 8 + 2 = 10. To express the term 2, we subtracted another term 8 from the sum of 10.
2 = 10 − 8
Now, to find the unknown x, we must subtract the known term 8 from the sum of 10:
x = 10 − 8
If you calculate the right side of the resulting equality, you can find out what the variable x is equal to
x = 2
We solved the equation. The value of the variable x is 2. To check, the value of variable x is sent to the original equation 8 + x = 10 and substituted for x. It is advisable to do this with any solved equation, because you cannot be sure that the equation is solved correctly:
The result is a correct numerical equality. So the equation is solved correctly.
The same rule would apply if the unknown was the first number 8.
x + 2 = 10
In this equation, x is the unknown, 2 is the known term, and 10 is the sum. To find the unknown x, subtract the known term 2 from the sum of 10
x = 10 − 2
x = 8
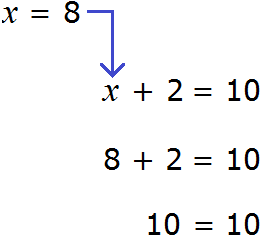
Let us return to the second example from the previous topic, where in the equality 8 - 2 = 6 we needed to express the number 8.
In equality 8 - 2 = 6, number 8 is a minuend, number 2 is a subtrahend, number 6 is the difference
To express the number 8, we did the following:
8 = 6 + 2
That is, we add the difference of 6 and the subtrahend of 2.
Now imagine that in the equality 8 - 2 = 6 instead of number 8 there is a variable x
x − 2 = 6
In this case, the variable x is the unknown minuend
The following rule is provided for finding the unknown minuend:
To find the unknown minuend, add the subtrahend to the difference.
That's what we did when we expressed the number 8 in 8 - 2 = 6. To express the minus of 8, we added the subtractor 2 to the difference of 6.
Now, to find the unknown minuend x, we must add the subtrahend 2 to the difference of 6.
x = 6 + 2
If you calculate the right-hand side, you can find out what the variable x is equal to
x = 8
Now imagine that in the equality 8 - 2 = 6 instead of number 2 there is a variable x
8 − x = 6
In this case, the variable x is the unknown subtrahend
The following rule is provided for finding the unknown subtrahend:
To find the unknown subtrahend, subtract the difference from the minuend.
This is what we did when we expressed the number 2 in 8 - 2 = 6. To express 2, we subtracted the difference of 6 from the minuend 8.
And now, to find the unknown subtrahend x, again subtract the difference of 6 from the minuend 8.
x = 8 − 6
Calculate the right-hand side and find the value of x
x = 2
Let's return to the third example from the previous topic, where in the equality 3 × 2 = 6 we tried to express the number 3.
In the equality 3 × 2 = 6 the numbers 3 and 2 are factors, the number 6 is the product of
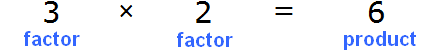
To express the number 3 we did the following:
That is, we divided the product of 6 by a factor of 2.
Now imagine that in the equality 3 × 2 = 6 instead of number 3 there is a variable x
x × 2 = 6
In this case, the variable x is the unknown factor.
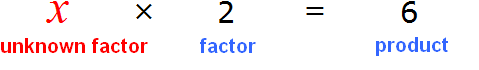
The following rule is provided for finding the unknown factor:
To find the unknown factor, divide the product by the factor.
This is what we did when we expressed the number 3 from the equation 3 × 2 = 6. We divided the product of 6 by a factor of 2.
Now to find the unknown factor x, divide the product of 6 by the factor 2.
Calculating the right hand side allows us to find the value of the variable x
x = 3
The same rule applies if the variable x is placed in place of any of the factors. Imagine that in the equality 3 × 2 = 6 there is a variable x instead of 2.
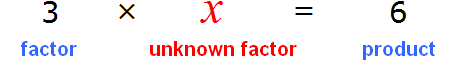
To find the unknown factor, divide the product by the factor.
This is what we did when we expressed the number 2 from the equality 3 × 2 = 6. Then to get number 2, we divided the product of 6 by the factor 3.
Now to find the unknown factor x, we divide the product of 6 by the factor 3.
Calculating the right-hand side of the equality allows you to know what x equals
x = 2
For example, solve the equation 9 × x = 18. The variable x is an unknown factor. To find this unknown factor, divide the product of 18 by the known factor 9
answer 
.
Solve the equation x × 3 = 27. The variable x is an unknown factor. To find this unknown factor, divide the product 27 by the known factor 3
answer 
.
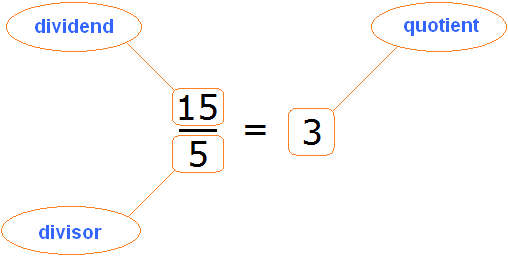
Let's return to the fourth example from the previous topic, where in equality we needed to express the number 15. In this equation, number 15 is the dividend, number 5 is the divisor, and number 3 is the quotient.
To express the number 15 we did the following:
15 = 3 × 5
That is, we multiplied the quotient of 3 by the divisor of 5.
Now imagine that in equality instead of the number 15 there is a variable x
In this case, the variable x is the unknown dividend.
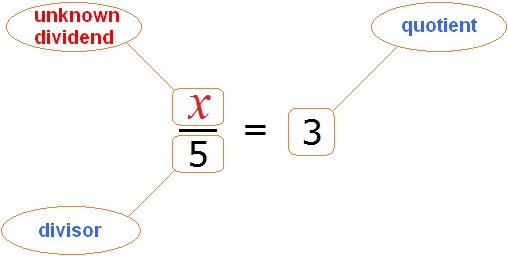
The following rule is provided for finding an unknown dividend:
To find the unknown dividend, multiply the quotient by the divisor.
That's what we did when we expressed 15 from equation . To express 15, we multiplied the quotient of 3 by the divisor of 5.
Now, to find the unknown dividend x, multiply the quotient of 3 by the divisor of 5.
x = 3 × 5
Calculate the right side of the resulting equality. In this way we will know what the variable x is equal to.
x = 15
Now imagine that in equality instead of number 5 there is a variable x.
In this case, the variable x is theunknown divisor.
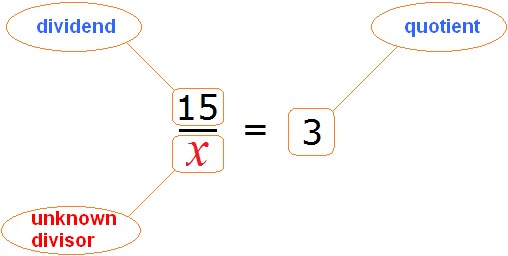
The following rule is provided for finding the unknown divisor:
To find the unknown divisor, divide the dividend by the quotient.
That's what we did when we expressed the number 5 from the equality . To express the number 5, we divided the dividend of 15 by the quotient of 3.
Now, to find the unknown divisor of x, divide the dividend of 15 by the quotient of 3.
Calculate the right side of the resulting equality. In this way we will know what the variable x is equal to.
x = 5
So, to find the unknowns, we learned the following rules:
- To find an unknown term, subtract a known term from the sum;
- To find the unknown minuend, add the subtrahend to the difference;
- To find the unknown subtrahend, subtract the difference from the minuend;
- To find the unknown factor, divide the product by the factor;
- To find the unknown dividend, multiply the quotient by the divisor;
- To find the unknown divisor, divide the dividend by the quotient.
Components
We will call the components the numbers and variables that make up the equality
Thus, the components of addition are the term and the sum
The components of subtraction are the minuend, the subtrahend, and the difference
The components of multiplication are the factors and the product
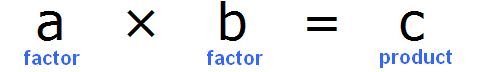
The components of division are the dividend, the divisor, and the quotient
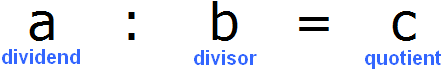
Depending on which components we will be dealing with, the corresponding rules for finding the unknowns will apply. We learned these rules in the previous topic. When solving equations, it is advisable to know these rules by heart.
Example 1. Find the root of the equation 45 + x = 60
45 is a term, x is an unknown term, and 60 is the sum. We are dealing with components of an addition. Recall that to find an unknown term, you must subtract the known term from the sum:
x = 60 − 45
Calculate the right hand side, we get the value of x equal to 15
x = 15
So the root of the equation 45 + x = 60 is 15.
More often than not, an unknown term must be reduced to a form in which it can be expressed.
Example 2. Solve the equation 
Here, unlike in the previous example, the unknown term cannot be expressed immediately because it contains a factor of 2. Our task is to reduce this equation to a form in which we can express x
In this example, we are dealing with the components of addition - the term and the sum. 2x is the first term, 4 is the second term, and 8 is the sum.
In this case the term 2x contains the variable x. After finding the value of variable x, the term 2x will take a different form. Therefore the term 2x can be completely taken as an unknown term:
Now we apply the rule of finding the unknown term. Subtract the known term from the sum:
Calculate the right side of the resulting equation:
We got a new equation . Now we are dealing with the components of multiplication: the factors, and the product. 2 - factor, x - factor, 4 - product
In this case, the variable x is not just a factor, but an unknown factor
To find this unknown factor, divide the product by the known factor:
Let's calculate the right hand side and get the value of the variable x
To check the found root, send to the original equation and substitute instead of x
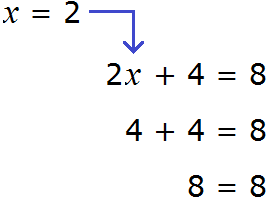
We obtained the correct numerical equality. So the equation is solved correctly.
Example 3. Solve the equation 3x + 9x + 16x = 56
It is not possible to express the unknown x immediately. First you must reduce the equation to a form in which it can be expressed.
Let us give like terms on the left side of this equation:
We are dealing with the components of multiplication. 28 is the factor, x is the factor, and 56 is the product. In this case x is an unknown factor. To find the unknown factor, divide the product by the known factor:
The answer is x equals 2
Equivalent equations
In the previous example, when solving the equation 3x + 9x + 16x = 56, we brought like terms to the left side of the equation. The result is the new equation 28x = 56. The old equation 3x + 9x + 16x = 56 and the new equation 28x = 56 are called equivalent equations because their roots are the same.
Equations are called equivalent if their roots are the same.
Let's check this. For the equation 3x + 9x + 16x = 56 we found a root of 2. Substitute this root first into the equation 3x + 9x + 16x = 56 and then into the equation 28x = 56, which was obtained by adding like terms to the left side of the previous equation. We should obtain the correct numerical equations
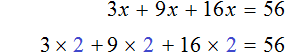
According to the order of operations, multiplication is performed first:
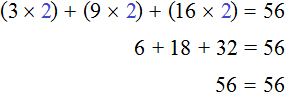
Substitute the root of 2 into the second equation 28x = 56
We see that both equations have the same roots. So the equations 3x + 9x + 16x = 56 and 28x = 56 are indeed equivalent.
To solve the equation 3x + 9x + 16x = 56, we used one of the identity transformations - the reduction of like terms. The correct identical transformation of the equation allowed us to obtain the equation 28x = 56, which is easier to solve.
The only identical transformations we know how to do at this point are to reduce fractions, to reduce like terms, to take the common factor out of parentheses, and to open brackets. There are other transformations that we should know. But for a general idea about identical transformations of equations, the topics we studied are enough.
Let us consider some transformations that allow us to obtain an equivalent equation
If you add the same number to both parts of the equation, you get an equation equal to this one.
and similarly:
If you subtract the same number from both parts of the equation, you get an equation equal to this one.
In other words, the root of the equation will not change if the same number is added to (or subtracted from) both parts of the equation.
Example 1. Solve the equation 
Subtract the number 10 from both parts of the equation
Let us give like terms in both parts:
We obtained the equation 5x = 10. We are dealing with the components of multiplication. To find the unknown factor x, divide the product of 10 by the known factor 5.
Answer .
Let's return to the original equation and substitute the found value of 2 for x
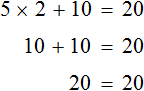
We obtained the correct numerical equality. So the equation is solved correctly.
By solving the equation we subtracted the number 10 from both parts of the equation. As a result, we got the equation 
. The root of this equation as well as the equation is 2
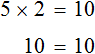
Example 2. Solve the equation 4(x + 3) = 16
Open the brackets on the left side of the equality:
Subtract the number 12 from both parts of the equation
Let us give like terms in both parts of the equation:
In the left part there will be 4x, and in the right part of the number 4
We obtain the equation 4x = 4. We are dealing with the components of multiplication. To find the unknown factor x, divide the product of 4 by the known factor 4
Answer 
Let's return to the original equation 4(x + 3) = 16 and substitute the value 1 for x
We obtained the correct numerical equality. So the equation is solved correctly.
Solving the equation 4(x + 3) = 16, we subtracted 12 from both parts of the equation. As a result, we obtained the equation 4x = 4. The root of this equation, like the equation 4(x + 3) = 16, is also 1.
Example 3. Solve the equation 
Open the brackets on the left side of the equality:
Add the number 8 to both parts of the equation
Let us give like terms in both parts of the equation:
The left side will contain 2x, and the right side will contain 9
In the resulting equation 2x = 9, express the unknown term x
Answer 
Let's return to the original equation and substitute the found value 4.5 for x
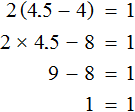
We obtained the correct numerical equality. So the equation is solved correctly.
Solving the equation we added the number 8 to both parts of the equation. As a result, we got the equation . The root of this equation, like the equation , is also 4.5
The following rule, which allows you to obtain an equal equation, is as follows
If you move the term in the equation from one part to the other, changing its sign, you get an equation that is equal to this one.
That is, the root of the equation will not change if we move a term from one part of the equation to another by changing its sign. This property is one of the most important and one often used in solving equations.
Consider the following equation:
The root of this equation is 2. Substitute this root for x and check if the numerical equation is correct
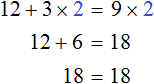
It turns out to be a correct equality. So the number 2 is really the root of the equation.
Now let's try to experiment with the terms of this equation by moving them from one part to the other, changing the signs.
For example, the term 3x is located on the left side of the equation. Move it to the right side, changing the sign to the opposite:
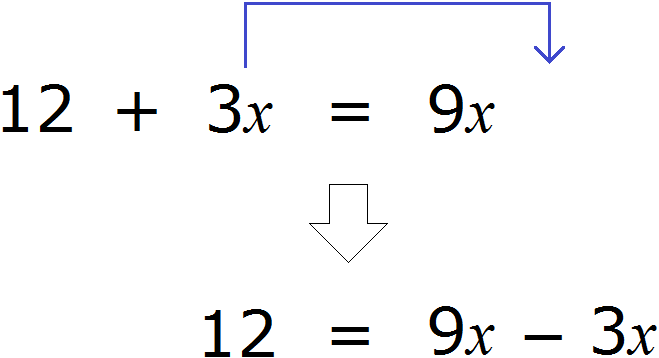
We obtain the equation 12 = 9x - 3x. Let's give the like terms in the right side of this equation:
We are dealing with multiplication components. The variable x is an unknown factor. Let's find this known factor:
Answer x = 2. As we see, the root of the equation has not changed. So the equations 12 + 3x = 9x and 12 = 9x - 3x are equivalent.
In fact, this transformation is a simplified method of the previous transformation, where the same number was added (or subtracted) to both parts of the equation.
We said that in the equation 12 + 3x = 9x the term 3x was moved to the right side by changing the sign. In reality, the following happened: the term 3x was subtracted from both parts of the equation
Then in the left part of the equation 12 = 9x - 3x. Then like terms were given again, but already in the right part, and the equation 12 = 6x is obtained.
But the so-called "transposition" is more convenient for like equations, which is why it is so widespread. When solving equations, we will often use exactly this transformation.
Equations 12 + 3x = 9x and 3x - 9x = -12 are also equal. This time in the equation 12 + 3x = 9x, the term 12 was moved to the right side and the term 9x to the left. Remember that the signs of these terms were changed during the transfer
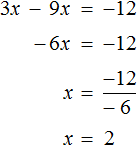
The following rule, which allows you to obtain an equation that is equivalent, is as follows:
If both parts of the equation are multiplied or divided by the same number that is not equal to zero, you get an equation equal to this one.
In other words, the roots of an equation will not change if both parts of it are multiplied or divided by the same number. This action is often used when you need to solve an equation that contains fractional expressions.
First, consider examples in which both parts of an equation are multiplied by the same number.
Example 1. Solve the equation 
When solving equations that contain fractional expressions, it is customary to first simplify the equation.
In this case, we are dealing with just such an equation. In order to simplify this equation, both parts of the equation can be multiplied by 8:
We remember that in order to multiply a fraction by a number, the numerator of the fraction must be multiplied by that number. We have two fractions and each of them is multiplied by the number 8. Our task is to multiply the numerators of the fractions by this number 8
Now the most interesting thing happens. The numerators and denominators of both fractions contain a factor of 8, which can be reduced by 8. This will allow us to get rid of the fractional expression:
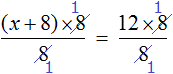
The result will be the simplest equation
And it is not hard to guess that the root of this equation is 4
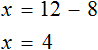
Let us return to the original equation and substitute the found value of 4 for x
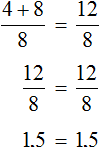
It turns out to be a correct numerical equality. So the equation is solved correctly.
In solving this equation, we multiplied both parts of the equation by 8. The result is the equation . The root of this equation, like the equation, is 4. So these equations are equal.
It is customary to write the factor by which both parts of the equation are multiplied before the part of the equation, not after it. So, solving the equation , we multiplied both parts of the equation by the factor 8 and got the following notation:
This did not change the root of the equation, but if we had done it at school, we would have received a note, because in algebra it is customary to write the factor before the expression with which it is multiplied. Therefore, it is advisable to rewrite the multiplication of both parts of the equation by the factor 8 as follows:
Example 2. Solve the equation 
Multiply both parts of the equation by 15
On the left side the factors 15 can be reduced by 15, and on the right side the factors 15 and 5 can be reduced by 5
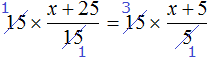
Let's rewrite what we have left:
Open the brackets in the right part of the equation:
Move the term x from the left side of the equation to the right side, changing its sign. And move the term 15 from the right side of the equation to the left side, again changing the sign:
If we add like terms in both parts, we obtain
We are dealing with multiplication components. The variable x is an unknown factor. Let's find it:
Answer 
Let's return to the original equation and substitute the found value 5 for x
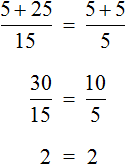
It turns out to be a correct numerical equality. So the equation is solved correctly. When solving this equation, we multiplied both parts of it by 15. Then by performing identical transformations, we got the equation 10 = 2x. The root of this equation as well as the equation is 5. So these equations are equivalent.
Example 3. Solve the equation 
Multiply both parts of the equation by 3
Two triples can be reduced on the left side, and the right side will be 18
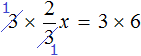
This leaves the simplest equation 2x = 18. We are dealing with the components of multiplication. The variable x is an unknown factor. Let's find it:
Answer
Let's return to the original equation and substitute the found value 9 for x
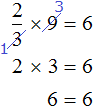
It turns out to be a correct numerical equality. So the equation is solved correctly.
Example 4. Solve the equation 
Multiply both parts of the equation by 6
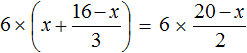
In the left part of the equation, open the brackets. On the right side, the factor 6 can be raised to the numerator:
Let's reduce in both parts of the equations what can be reduced:
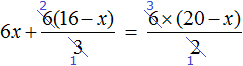
Let's rewrite what we have left:
Open the brackets in both parts of the equation:
We will use the transfer of terms. We group the terms containing the unknown x on the left side of the equation, and the terms free of unknowns on the right side:
Let us give like terms in both parts:
Now find the value of the variable x. To do this, divide the product of 28 by the known factor 7
Answer x = 4.
Let's return to the original equation and substitute the found value of 4 for x
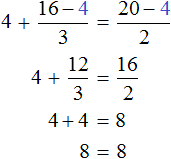
The numerical equality is correct. So the equation is solved correctly.
Example 5. Solve the equation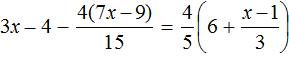 
Open brackets in both parts of the equation, where possible:
Multiply both parts of the equation by 15
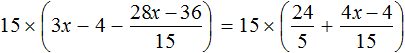
Open the brackets in both parts of the equation:
Let's reduce in both parts of the equation what can be reduced:
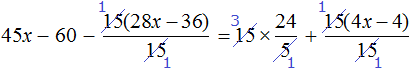
Let's rewrite what we have left:
Open brackets where you can:
We will use the transfer of terms. We group the terms containing the unknown in the left part of the equation, and the terms free of unknowns in the right part of the equation. Don't forget that during the transposition, the terms change their signs to the opposite:
Let us give like terms in both parts of the equation:
Let's find the value of x
In the resulting answer, you can select the whole part:
Let's return to the original equation and substitute the found value 
for x
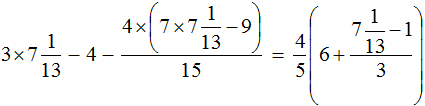
This turns out to be a rather cumbersome expression. Let's use variables. Let's write the left part of the equation to variable A, and the right part of the equation to variable B
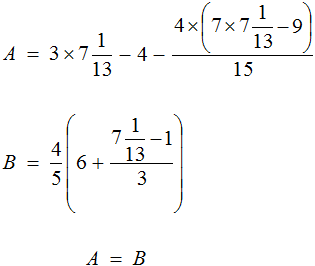
Our task is to see if the left-hand side is equal to the right-hand side. In other words, prove the equality A = B
Find the value of the expression in variable A.
The value of variable A is 
. Now find the value of variable B. That is, the value of the right side of our equality. If it is also , then the equation is solved correctly
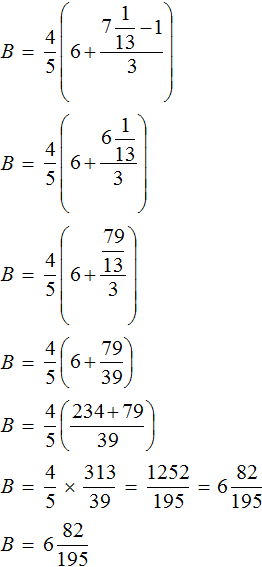
We see that the value of variable B, like the value of variable A, is . This means that the left side is equal to the right side. From this we conclude that the equation is solved correctly.
Now let's try not to multiply both parts of the equation by the same number, but to divide it.
Consider the equation 30x + 14x + 14 = 70x - 40x + 42. Solve it by the usual method: group the terms containing unknowns on the left side of the equation, and the terms free of unknowns on the right side. Then by performing the known identity transformations we find the value of x
Substitute the found value of 2 instead of x into the original equation:
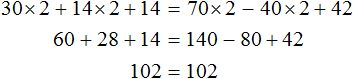
Now try to divide all terms of the equation 30x + 14x + 14 = 70x - 40x + 42 by some number. Note that all terms of this equation have a common factor of 2. Divide each term in this equation by it:
Let's perform the reduction in each term:
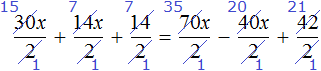
Let's rewrite what we have left:
Let us solve this equation using the known identity transformations:
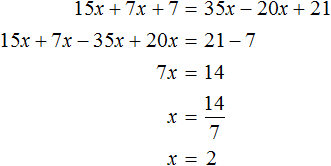
We got the root of 2. So the equations 15x + 7x + 7 = 35x - 20x + 21 and 30x + 14x + 14 = 70x - 40x + 42 are equivalent.
Dividing both parts of the equation by the same number allows us to free the unknown from the quotient. In the previous example, when we got the equation 7x = 14, we needed to divide the product of 14 by the known factor 7. But if we were to free the unknown from the quotient of 7 on the left side, the root could be found immediately. To do this, it would be enough to divide both parts by 7
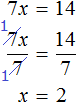
We will use this method often, too.
Multiplication by minus one
If you multiply both parts of the equation by minus one, you get an equation equal to this one.
This rule follows from the fact that by multiplying (or dividing) both parts of an equation by the same number, the root of the equation does not change. This means that the root does not change if both parts of the equation are multiplied by -1.
This rule allows you to change the signs of all the components in the equation. What is this for? Again, to get an equivalent equation that is easier to solve.
Consider the equation 
. What is the root of this equation?
Add the number 5 to both parts of the equation
Let us give like terms:
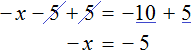
Now let's think about the quotient of the algebraic expressions.What is the left side of the equation 
. It is the product of minus one and the variable x
That is, the minus in front of the variable x does not refer to the variable x itself, but to the unit, which we do not see because it is customary not to write the coefficient 1. This means that the equation actually looks like this:
We are dealing with the components of multiplication. To find x, divide the product -5 by the known factor -1.
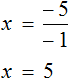
or divide both parts of the equation by -1, which is even easier
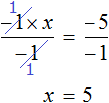
So, the root of the equation is 5. To check it, substitute it into the original equation. Remember that in the original equation the minus in front of the variable x refers to the invisible unit
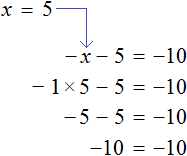
The numerical equality is correct. So the equation is solved correctly.
Now let's try to multiply both parts of the equation by minus one:
After opening the brackets, the expression 
will be formed on the left side, and the right side will be equal to 10
The root of this equation, as well as the equation is 5
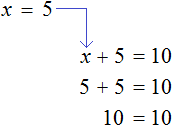
So equations and 
are equivalent.
Example 2. Solve the equation 
All components in this equation are negative. It is more convenient to work with positive components than with negative ones, so let's change the signs of all the components that make up the equation . To do this, multiply both parts of this equation by -1.
It is clear that multiplication by -1 will cause any number to change its sign to the opposite. Therefore, the procedure of multiplication by -1 and the opening of brackets is not described in detail, but the components of the equation with opposite signs are written immediately.
Thus, the multiplication of the equation by -1 can be written in detail as follows:
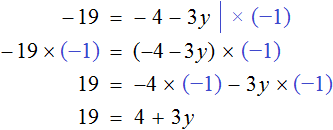
or you can just change the signs of all the components:
It will be the same, but the difference will be that we will save ourselves time.
So, by multiplying both parts of the equation by -1, we obtain the equation . Let's solve this equation. Subtract 4 from both parts and divide both parts by 3.
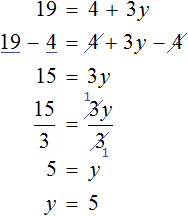
When a root is found, the variable is usually written on the left side and its value on the right side, which is what we did.
Example 3. Solve the equation 
Multiply both parts of the equation by -1. Then all components will change their signs to the opposite:
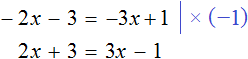
Subtract 2x from both parts of the resulting equation and add similar terms:
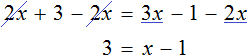
Let's add one to both parts of the equation and add like terms:
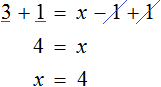
Equating to zero
We recently learned that if you move a term from one part of an equation to another by changing its sign, you get an equation that is equal to this one.
And what happens if you move all of the terms from one part to the other? That's right, zero remains in the part where all the terms were taken from. In other words, there would be nothing left.
As an example, consider the equation 
. Solve this equation as usual - group the terms containing the unknowns in one part, and leave the numeric terms free of unknowns in the other part. Then we perform the well-known identity transformations to find the value of the variable x
Now let us try to solve the same equation by equating all its components to zero. To do this, move all the terms from the right side to the left side, changing the signs:
Let us give like terms in the left part:
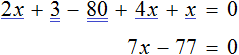
Add 77 to both parts, and divide both parts by 7
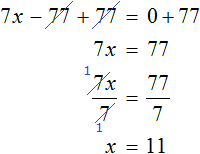
Alternative to the rules for finding the unknowns
Obviously, knowing the identity transformations of equations, you don't have to learn by heart the rules for finding the unknowns.
For example, to find an unknown in an equation 
, we divide the product of 10 by a known factor of 2
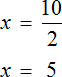
But if you divide both parts of the equation by 2, the root is found immediately. On the left side of the equation, the numerator factor of 2 and the denominator factor of 2 will be reduced by 2. And the right side will equal 5
We solved equations of the form by expressing the unknown term:
But you can use the identity transformations we studied today. In the equation , the summand 4 can be moved to the right side by changing the sign:
Then divide both parts by 2
The left side of the equation will be reduced by two twos. The right side will be 2. The answer is .
Or you could subtract 4 from both parts of the equation. Then the result would be the following:
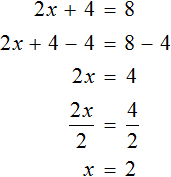
In the case of equations of the form , it is more convenient to divide the product by a known factor. Let us compare both solutions:
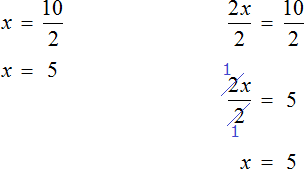
The first solution is much shorter and neater. The second solution can be greatly shortened by doing the division in your mind.
Nevertheless, you need to know both methods, and only then use the one you like best.
When there are several roots
An equation can have multiple roots. For example, the equation x(x + 9) = 0 has two roots: 0 and -9.
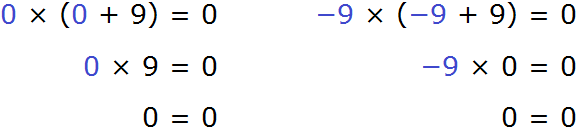
In the equation x(x + 9) = 0, we needed to find a value of x where the left-hand side would be zero. The left side of this equation contains the expressions x and (x + 9), which are the factors. We know from the laws of multiplication that a product is zero if at least one of the factors is zero (either the first factor or the second factor).
That is, in the equation x(x + 9) = 0, equality will be achieved if x equals zero or if (x + 9) equals zero.
x = 0 or x + 9 = 0
By equating both of these expressions to zero, we can find the roots of the equation x(x + 9) = 0. The first root, as you can see from the example, is found immediately. To find the second root we need to solve the elementary equation x + 9 = 0. It is not difficult to guess that the root of this equation is -9. A check shows that the root is correct:
−9 + 9 = 0
Example 2. Solve the equation 
This equation has two roots: 1 and 2. The left side of the equation is the product of (x - 1) and (x - 2). And the product is zero if at least one of the factors is zero (either the factor (x - 1) or the factor (x - 2)).
Find x such that the expressions (x - 1) or (x - 2) are zero:
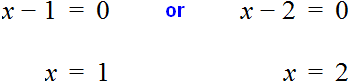
We substitute these values one by one into the original equation and make sure that at these values the left-hand side is zero:
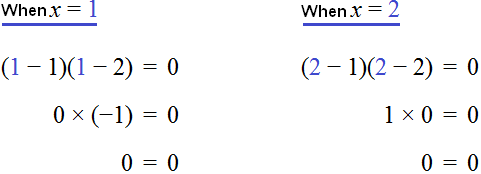
When the roots are infinitely many
An equation can have infinitely many roots. That is, by substituting any number into such an equation, we will obtain a correct numerical equality.
Example 1. Solve the equation 
The root of this equation is any number. If you open the brackets on the left side of the equation and add like terms, you get the equality 14 = 14. This equality will be obtained for any x
Example 2. Solve the equation 
The root of this equation is any number. If you open the brackets on the left side of the equation, you get the equality 10x + 12 = 10x + 12. This equality will be obtained for any x
When there are no roots
It also happens that an equation has no solutions at all, that is, it has no roots. For example, the equation x+2=x has no roots, because for any value of x, the left side of the equation will not equal the right side. For example, let x=2. Then the equation would look like this
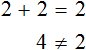
Let x = -4
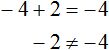
Example 2. Solve the equation 
Open the brackets on the left side of the equality:
Let us give like terms:
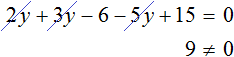
We see that the left part is not equal to the right part. This will be true for any value of y. For example, let y = 3.
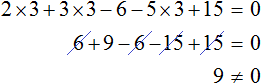
Letter equations
An equation can contain not only numbers with variables, but also letters.
For example, the formula for finding velocity is a letter equation:
This equation describes the velocity of the body in equi-accelerated motion.
It is a useful skill to be able to express any component that is part of a letter equation. For example, to determine the distance from the equation , you need to express the variable s.
Multiply both parts of the equation by t
In the right part, reduce the variables t by t and rewrite what we have left:
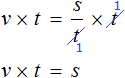
In the resulting equation, swap the left and right parts:
We got the formula for finding the distance that we studied earlier.
Let's try to determine the time from the equation . To do this, we need to express the variable t.
Multiply both parts of the equation by t
In the right part, reduce the variables t by t and rewrite what we have left:
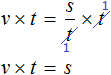
In the resulting equation v × t = s, divide both parts by v
On the left side, reduce the variables v by v and rewrite what we have left:
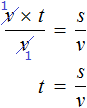
We got the formula for finding time that we studied earlier.
Suppose the speed of the train is 50 km/h
v = 50 km/h
And the distance is 100 km
s = 100 km
Then the alphabetic equation will take the following form
From this equation you can find the time. To do this, we need to be able to express the variable t. You can use the rule of finding the unknown divisor by dividing the dividend by the quotient and thus determine the value of the variable t
or it is possible to use identity transformations. First, multiply both parts of the equation by t
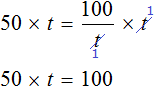
Then divide both parts by 50
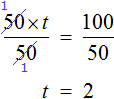
Example 2. The letter equation a+bx=c is given. Express from this equation x
Subtract a from both parts of the equation
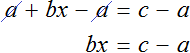
Divide both parts of the equation by b
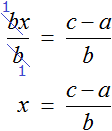
Now, if we find an equation of the form a + bx = c, we have a ready solution. It will be enough to substitute the required values into it. Those values that will be substituted for the letters a, b, c are called parameters. Equations of the form a + bx = c are called equations with parameters. Depending on the parameters, the root will change.
Solve the equation 2 + 4x = 10. It is similar to the letter equation a + bx = c. Instead of performing identity transformations, we can use a ready-made solution. Let's compare both solutions:
We see that the second solution is much simpler and shorter.
For the ready solution we need to make a small note. The parameter b must not be equal to zero (b ≠0), since division by zero is not allowed.
Example 3. An literal equation is given 
x
Open the brackets in both parts of the equation
Let us take advantage of the transfer of terms. We group the parameters containing the variable x on the left side of the equation, and the parameters free of this variable on the right side.
On the left side, put the factor x behind the brackets.
Divide both parts by the expression a - b
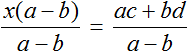
The left part of the numerator and denominator can be reduced by a - b. This is the final expression of the variable x
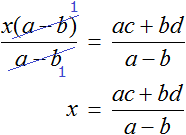
Now, if we find an equation of the form a(x - c) = b(x + d), we have a ready solution. All we have to do is to substitute the desired values into it.
Suppose we are given the equation 4(x - 3) = 2(x + 4). It is similar to the equation a(x - c) = b(x + d). Solve it in two ways: using identity transformations and using a ready-made solution:
For convenience, we take the values of parameters a, b, c, d out of the equation 4(x - 3) = 2(x + 4). This will allow us not to make a mistake when substituting:
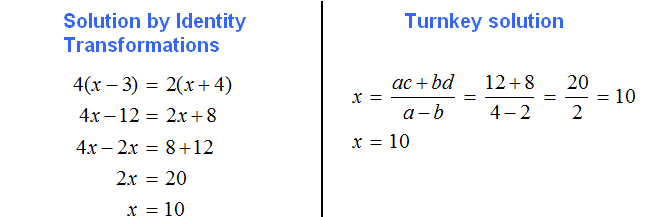
As in the last example, the denominator here must not be equal to zero (a - b ≠0). If we encounter an equation of the form a(x - c) = b(x + d) in which the parameters a and b are the same, we can say without solving it that the equation has no roots, since the difference of the same numbers is zero.
For example, the equation 2(x - 3) = 2(x + 4) is an equation of the form a(x - c) = b(x + d). In the equation 2(x - 3) = 2(x + 4), the parameters a and b are the same. If we start solving it, we will come to the fact that the left part is not equal to the right part:
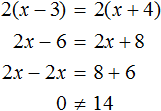
Example 4. An literal equation is given 
. Express from this equation x
Let's reduce the left part of the equation to a common denominator:
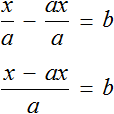
Multiply both parts by a
In the left part of x, put it outside the brackets.
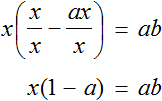
Divide both parts by the expression (1 - a)
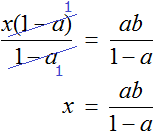
Linear equations with one unknown
The equations discussed in this lesson are called first-degree linear equations with one unknown.
If an equation is given to the first degree, contains no division by the unknown, and contains no roots from the unknown, then it can be called linear. We haven't yet studied degrees and roots, so in order not to complicate our lives, we will understand the word "linear" to mean "simple".
Most of the equations solved in this lesson eventually boiled down to a simple equation in which you had to divide the product by a known factor. This is, for example, the equation 2(x + 3) = 16. Let's solve it.
Open the brackets on the left side of the equation, we obtain 2x + 6 = 16. Move the term 6 to the right part of the equation by changing the sign. Then we obtain 2x = 16 - 6. Calculate the right side, we obtain 2x = 10. To find x, divide the product of 10 by a known factor 2. The answer is x = 5.
The equation 2(x + 3) = 16 is linear. It is reduced to the equation 2x = 10, in order to find the root of which it was necessary to divide the product by a known factor. Such a simple equation is called a first-degree linear equation with one unknown in canonical form. The word "canonical" is synonymous to the words "simplest" or "normal".
A first-degree linear equation with one unknown in canonical form is called an equation of the form ax = b.
The equation we obtain, 2x = 10, is a first-degree linear equation with one unknown in canonical form. This equation has the first degree, one unknown, contains no division by the unknown, contains no roots of the unknown, and is presented in canonical form, that is, in the simplest form in which you can easily determine the value of x. Instead of the parameters a and b, our equation contains the numbers 2 and 10. But a similar equation can contain other numbers: positive, negative, or equal to zero.
If a = 0 and b = 0 in a linear equation, then the equation has infinitely many roots. Indeed, if a equals zero and b equals zero, then the linear equation ax = b will take the form 0x = 0. For any value of x, the left-hand side will be equal to the right-hand side.
If a = 0 and b ≠0 in a linear equation, then the equation has no roots. Indeed, if a equals zero and b equals some number not equal to zero, say number 5, then the equation ax = b will take the form 0x = 5. The left side would be zero and the right side would be five. And zero is not equal to five.
If in a linear equation a ≠0, and b equals any number, the equation has one root. It is determined by dividing the parameter b by the parameter a
Indeed, if a equals some number other than zero, say number 3, and b equals some number, say number 6, then the equation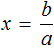 
will look like 
Answer .
There is another form of a first-degree linear equation with one unknown. It looks like this: ax - b = 0. This is the same equation as ax = b, but the parameter b is moved to the left side with the opposite sign. We solved such equations in this lesson as well. For example, the equation 7x - 77 = 0. An equation of the form ax - b = 0 is called a first-degree linear equation with one unknown in general form.
In the future, after we study rational expressions, we will look at such concepts as extraneous roots and loss of roots. For now, this lesson will suffice.
Tasks for independent decision
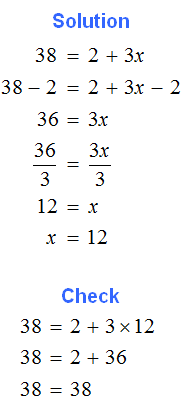
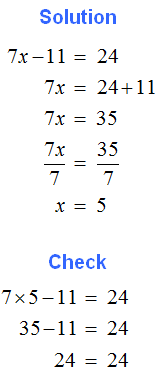
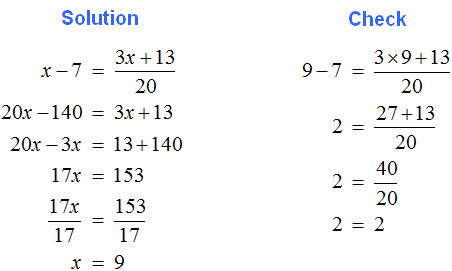
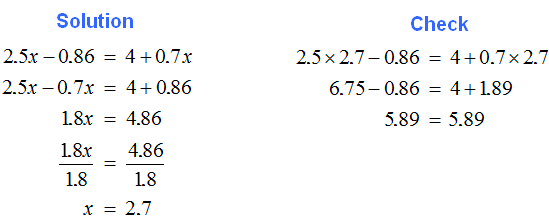
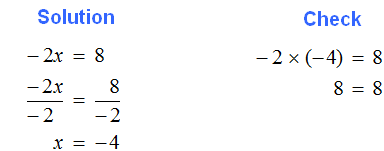
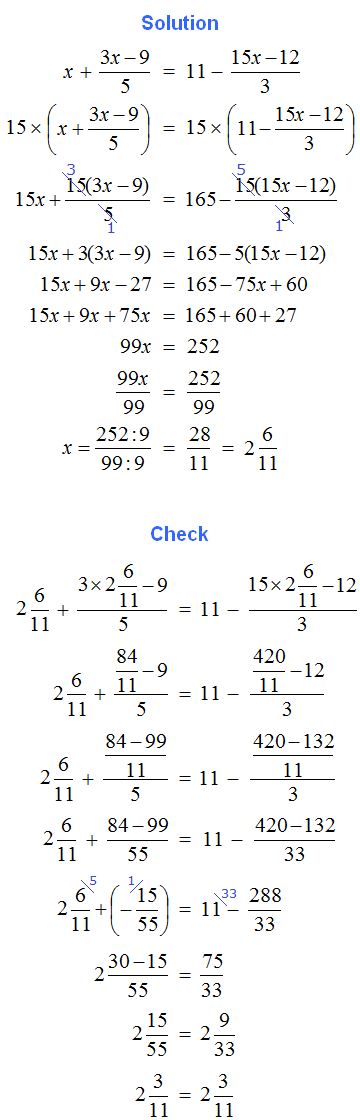
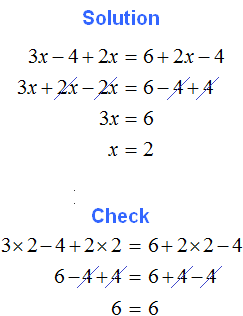
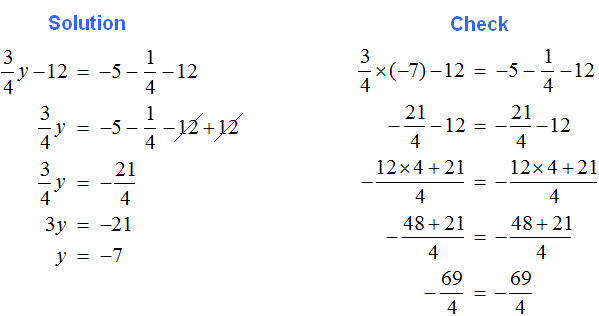
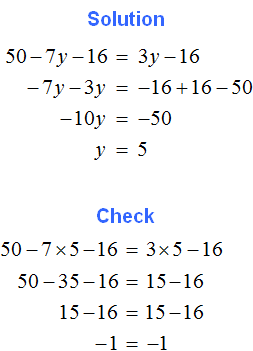
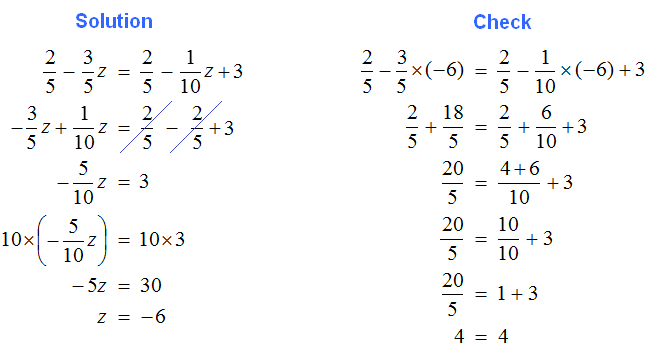
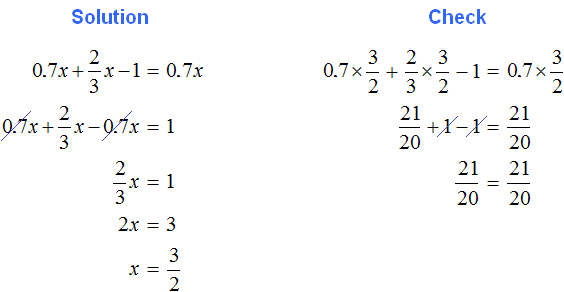
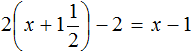
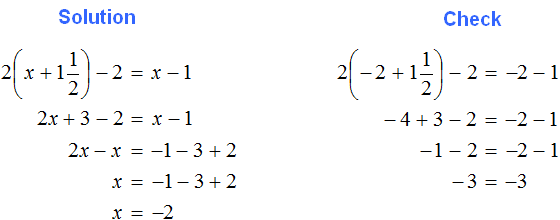
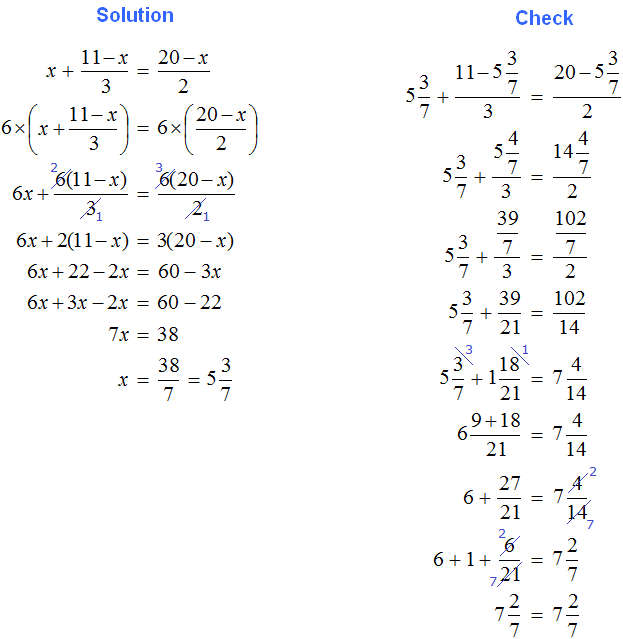
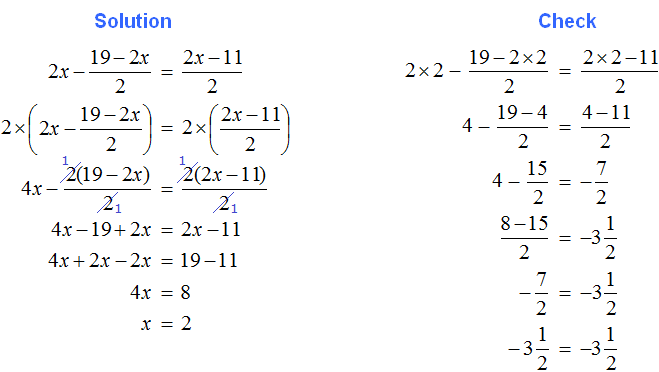
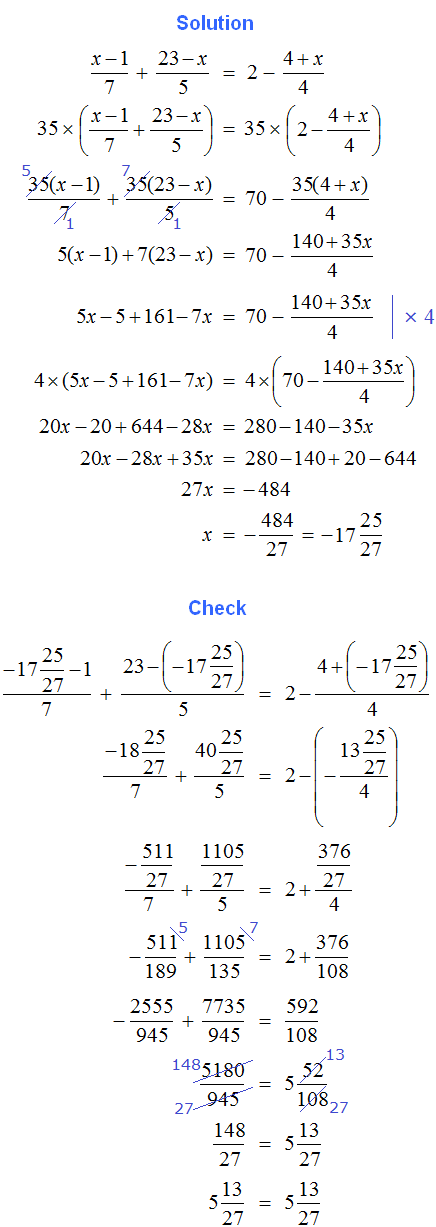
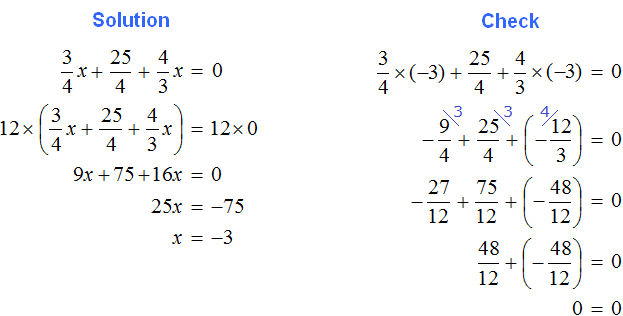
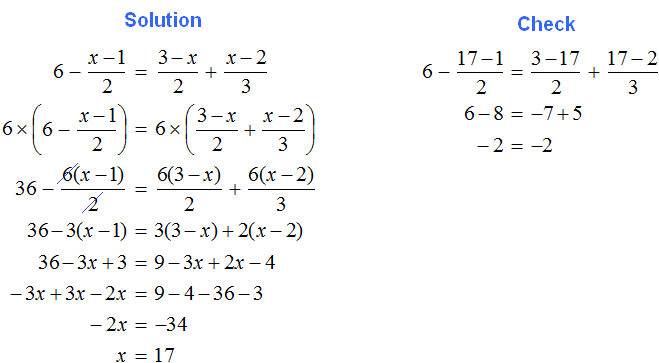
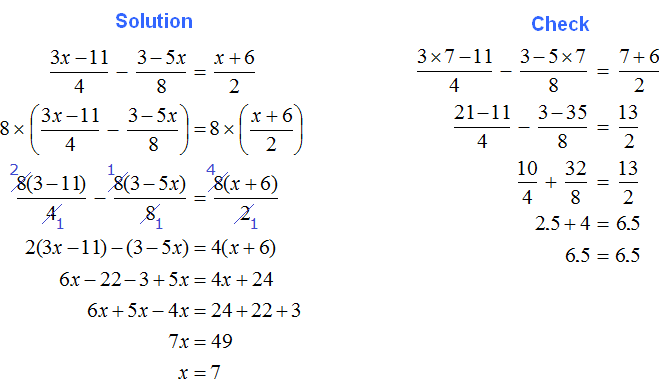
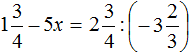
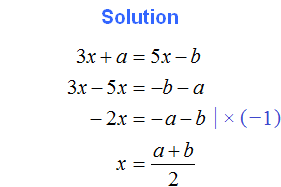
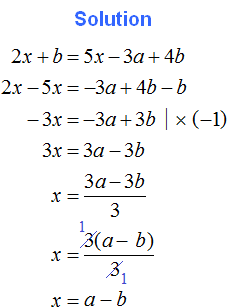
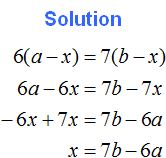
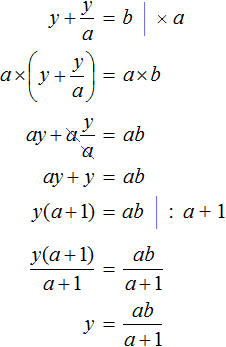
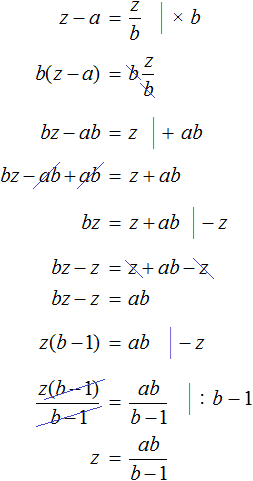
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.