Comparing Rational Numbers

We continue studying rational numbers. In this lesson we will learn how to compare them.

From the previous lessons we learned that if a particular number is farther to the right on the number line than is another number, then the first number is greater than the seconds. 

For example, if you compare the numbers 4 and 1, you can immediately answer that 4 is greater than 1. This is a perfectly logical statement and everyone would agree with it.

As proof of this, we can use a number line. On it you can see that the four lies to the right of the one

4 > 1

There is also a rule for this case, which you can use if you want. It looks like this:

To compare two positive integers, the positive integer with the larger number is greater.

For example, compare the same numbers 4 and 1, applying the above rule

Compare integers:

4 > 1

Result:

4 > 1

There is another rule for negative numbers, and it looks like this:

To compare two negative integers, the negative integer with the less modulus is greater.

For example, compare the numbers -3 and -1

Find the modulus of the numbers

|−3| = 3

|−1| = 1

Compare them:

3 > 1

Result:

−3 < −1

Do not confuse the modulus of a number with the number itself. This is a common mistake made by many beginners.

For example, if the modulus of the number -3 is greater than the modulus of the number -1, it does not mean that the number -3 is greater than the number -1.

The number -3 is smaller than the number -1. This can be understood by using the number line

You can see that the number -3 is to the left of -1. And we know that If a particular number is farther to the left on the number line than is another number, then the first number is less than the second (equivalently, the second is greater than the first)

If you compare a negative number to a positive number, the answer is self-evident. Any negative number will be less than any positive number. For example, -4 is less than 2

−4 < 2

You can see that -4 is to the left of 2. 

The first thing to look at here is the signs of the numbers. A minus in front of the number will tell you that the number is negative. If there is no number sign, the number is positive, but you can write it down for clarity. Recall that it is a plus sign

−4 < +2

We have considered examples of integers: -4, -3 -1, 2. It is not very difficult to compare such numbers, as well as to represent them on the number line.

It is much harder to compare other kinds of numbers, such as fractions, mixed numbers, and decimals, some of which are negative. Here you will mostly have to apply rules, because it is not always possible to accurately represent such numbers on a number line. In some cases, the number will need to be modified to make it easier to compare and perceive.

Example 1. Compare rational numbers   and 

So, we need to compare a negative number with a positive number. Any negative number is smaller than any positive number. Therefore, without wasting time we answer that is less than

Example 2. Compare rational numbers   and 

You need to compare two negative numbers. If we compare two negative numbers, the one whose modulus is less is greater.

Find modules of numbers:

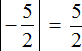
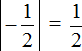
Compare these modules:

 So the rational number is greater than because the modulus of is less than the modulus of

Example 3. Compare numbers 2.35 and

It is required to compare a positive number with a negative number. Any positive number is greater than any negative number. Therefore, without wasting time we answer that 2.35 is greater than

2.35 > 

Example 4. Compare rational numbers   and

You need to compare two negative numbers. If we compare two negative numbers, the number whose modulus is less is greater.

Find modules of numbers:

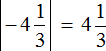
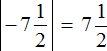
Compare the modules we found. But first, let's convert to an understandable form, so that it is easier to compare them, namely, let's convert them into improper fraction and convert to a common denominator

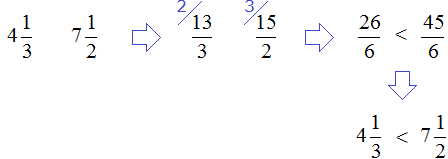
So the rational number  is greater than  because the modulus of  is less than the modulus of

Example 5. Compare rational numbers 0 and

It is required to compare zero with a negative number. Zero is greater than any negative number, so without wasting time we answer that 0 is greater than 

Example 6. Compare the rational numbers 0 and  

It is required to compare zero with a positive number. Zero is less than any positive number, so without wasting time we answer that 0 is less than

Example 7. Compare rational numbers 4.53 and 4.403

It is required to compare two positive numbers. To compare two positive integers, the positive integer with the larger number is greater.

Make the number of digits after the point the same in both fractions. To do this, add one zero at the end of the fraction 4.53

4.530

Then we apply the rule of comparing positive numbers.

Just compare them:

 So the rational number 4.53 is greater than 4.403 because the number of 4.53 is greater than the number of 4.403.

4.53 > 4.403

Example 8. Compare rational numbers   and

You need to compare two negative numbers. To compare two negative integers, the negative integer with the less modulus is greater.

Find the modules of numbers:

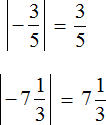
Compare the modules we found. But first, let's convert them to an understandable form, so that it is easier to compare, namely, let's convert the mixed number into an improper fraction, and then convert both fractions to a common denominator:

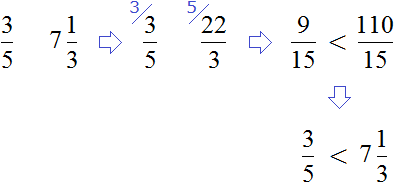
So the rational number is greater than because the modulus of is less than the modulus of

Comparing decimals is much easier than comparing fractions and mixed numbers. In some cases, by looking at the integer part of such a fraction, you can immediately answer the question which fraction is larger and which is smaller.

To do this, you need to compare the integer numbers of the whole parts. This will quickly answer the question in the problem. After all, as we know, whole parts in decimals have more weight than fractions.

Example 9. Compare rational numbers 15.4 and 2.1256

Lets compare integer numbers

15 > 2

that's why the fraction 15.4 is larger than the fraction 2.1256

15,4 > 2.1256

In other words, we did not have to waste time writing the zeros of the fraction 15.4 and compare the resulting fractions like regular numbers

15.4000   2.1256

154000 > 21256

The comparison rules are still the same. In our case we were comparing positive numbers.

Example 10. Compare rational numbers -15.2 and -0.152

You need to compare two negative numbers. 

|−15| = 15

|−0| = 0

15 > 0

We see that the modulus of the integer part of the fraction -15.2 is greater than the modulus of the integer part of the fraction -0.152.

So the rational -0.152 is greater than -15.2 because the modulus of the integer part of -0.152 is less than the modulus of the integer part of -15.2.

 −0.152 > −15.2

Example 11. Compare rational numbers -3.4 and -3.7

Two negative numbers must be compared. 

|−3| = 3

|−3| = 3

3 = 3

In this case we have to use the old method: find the modules of rational numbers and compare these modules

|−3.4| = 3.4

|−3.7| = 3.7

Compare the modules found:

According to the rule, of two negative numbers, the number whose modulus is less is greater. So the rational -3.4 is greater than -3.7 because the modulus of -3.4 is less than the modulus of -3.7.

−3.4 > −3.7

Example 12. Compare rational numbers 0.(3) and  

It is required to compare two positive numbers. And compare a recurring decimals with a fraction.

Convert the recurring decimals 0.(3) to a fraction and compare it to the fraction . After converting the recurring decimals 0.(3) to an fraction, it is converted to fraction 

Find the modules of numbers:

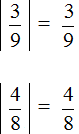
Let's compare the modules we found. But first, let's bring them to an understandable form, so that it is easier to compare them, namely, let's reduce them to a common denominator:

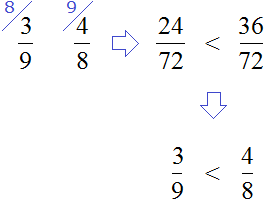
According to the rule, To compare two positive integers, the positive integer with the larger number is greater. So the rational number is greater than 0.(3) because the number of is greater than the number of 0.(3)

0.(3)  < 

Video lesson

Add comment