We continue to study elementary math tasks. This lesson is about percentage tasks. We will look at several tasks, as well as touch on things we didn't mention earlier when studying percentages, considering that they pose a challenge to learning at first.
Most percentage tasks boil down to finding a percentage of a number, finding a number by a percentage, expressing a part of it as a percentage, or expressing the relationship between several objects, numbers, and quantities as a percentage.
Ways to find the percentage
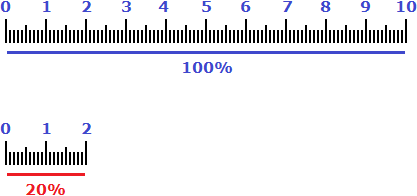
Percentages can be found in various ways. The most popular way is to divide the number by 100 and multiply the result by the number of percentages you are looking for.
For example, to find 60% of $200, you must first divide that $200 into one hundred equal parts:
$200 : 100 = $2.
When we divide a number by 100, we thereby find one percent of that number.
For example, by dividing $200 into 100 parts, we automatically found 1% of two hundred dollars, that is, we found out how many dollars are in one part. As you can see from the example, one part (one percent) is $2.
1% of $200 - $2
Knowing how many dollars are in one part (the 1%), you can find out how many dollars are in two parts, in three, in four, in five, etc. That is, you can find any number of percentages. To do this, just multiply those $2 dollars by the number of parts (percentages) you are looking for. Let's find sixty parts (60%)
$2 × 60 = $120
Let's find 5%
$2 × 5 = $10
Let's find 90%
$2 × 90 = $180
Let's find 100%
$2 × 100 = $200
100% is all one hundred pieces and they are all $200.
The second way is to represent the percentage as an ordinary fraction and find that fraction from the number from which you want to find the percentage.
For example, find the 60% of $200.
First, let's represent 60% as an ordinary fraction. Sixty percent is sixty parts of a hundred, i.e. sixty hundredths:
![]()
Now the task can be understood as "find ![]() of $200". This is finding a fraction of the number we studied earlier. Recall that to find a fraction of a number, you must divide the number by the denominator of the fraction and multiply the result by the numerator of the fraction
of $200". This is finding a fraction of the number we studied earlier. Recall that to find a fraction of a number, you must divide the number by the denominator of the fraction and multiply the result by the numerator of the fraction
200 : 100 = 2
2 × 60 = 120
Either multiply a number by a fraction (a quick way to find a fraction of a number):
![]()
The third way is to represent the percentage as a decimal and multiply the number by that decimal.
For example, find the same 60% of $200. First, we represent the 60% as a fraction. Sixty percent is sixty parts of a hundred.
![]()
Perform division in this fraction. Move the point in number 60 two digits to the left:
![]()
Now we find 0.60 of $200. To find the decimal of a number, multiply that number by the decimal:
200 × 0.60 = $120
The above method of finding the percentage is the most convenient, especially if a person is used to using a calculator. This method allows you to find the percentage in one step.
As a rule, it is not very difficult to express the percentage in a decimal. It is enough to add "zero integers" in front of the percentage if the percentage is a two-digit number, or to add "zero integers" and another zero if the percentage is a one-digit number.
Examples:
60% = 0.60 - we put zero integers before number 60 because number 60 is two-digit.
6% = 0.06 - added zero integers and one more zero before number 6 because number 6 is one-digit.
When dividing by 100, we used the method of moving the dot two digits to the left. In the answer 0.60 the zero after the digit 6 is preserved. But if we do this division, the zero disappears - the answer is 0.6
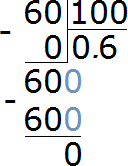
Remember that the decimal 0.60 and 0.6 are equal to the same value:
0.60 = 0.6
In this example, you can continue dividing indefinitely, adding zero to the remainder each time, but that would be a meaningless action:
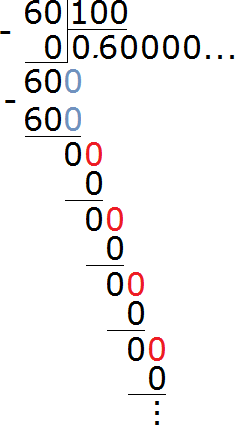
You can express percentages as decimals not only by dividing by 100, but also by multiplying. The percent sign (%) itself replaces the multiplier 0.01. And if we take into account that the number of percent and the percent sign are written together, then an "invisible" multiplication sign (×) is placed between them.
So, the 45% entry actually looks like this:
![]()
Replace the percent sign with a multiplier of 0.01
![]()
This multiplication by 0.01 is done by moving the point two digits to the left:
![]()
Task 1. The family has a budget of $175,000 per year Of that, 70% is money earned by dad. What part did mom earn?
Solution.
A total of 100 percent. If dad earned 70% of the money, then mom earned the other 30% of the money.
Task 2. The family has a budget of $175,000 per year. Of that, 70% is money earned by dad, and 30% is money earned by mom. How much money did each person earn?
Solution
Let's find 70% and 30% of the $175,000. This is how we will determine how much money each earned. For convenience, let's write 70% and 30% as decimals:
175 × 0.70 = $122.5 K (dad earned)
175 × 0.30 = $52.5 K (mom earned)
Check
122.5 + 52.5 = 175
175 = 175
Answer: $122,500 was earned by Dad and $52,500 was earned by Mom.
Task 3. When the bread cools, it loses up to 4% of its mass due to evaporation of water. How many kilograms will evaporate when 12 tons of bread cools.
Solution
Let's convert 12 tons to kilograms. One ton has 1,000 kilograms, and 12 tons has 12 times that amount:
1,000 × 12 = 12,000 kg.
Now let's find 4% of 12,000. The result will be the answer to the problem:
12,000 × 0.04 = 480 kg
Answer: when 12 tons of bread cools, 480 kg will evaporate.
Task 4. Apples lose 84% of their mass when dried. How many dried apples do you get from 300 kg of fresh apples?
Find 84% of 300 kg.
300 : 100 × 84 = 252 kg.
As a result of drying 300 kg of fresh apples will lose 252 kg of their mass. To answer the question how much dried apples we have, subtract 252 from 300
300 - 252 = 48 kg.
Answer: 300 kg of fresh apples will give you 48 kg of dried apples.
Task 5. Soybean seeds contain 20% oil. How much oil is contained in 700 kg of soybeans?
Solution
Find 20% of 700 kg
700 × 0.20 = 140 kg
Answer: 700 kg of soybeans contains 140 kg of oil
Task 6. Buckwheat groats contain 10% proteins, 2.5% fats, and 60% carbohydrates. How many of these products are in 14.4 quintals of buckwheat groats?
Solution
Let's convert 14.4 quintals to kilograms. One quintal has 100 kilograms, 14.4 quintals has 14.4 times more
100 × 14.4 = 1440 kg
Let's find 10%, 2.5% and 60% of 1440 kg
1440 × 0.10 = 144 (kg of protein)
1440 × 0.025 = 36 (kg of fat)
1440 × 0.60 = 864 (kg of carbohydrates)
Answer: 14.4 quintals of buckwheat groats contains 144 kg of protein, 36 kg of fat, and 864 kg of carbohydrates.
Task 7. Students collected 60 kg of seeds of oak, acacia, linden, and maple. Acorns made up 60%, maple seeds 15%, linden seeds 20% of all seeds, and the rest were acacia seeds. How many kilograms of acacia seeds were collected by the students?
Solution
Let's take oak, acacia, linden, and maple seeds as 100%. Subtract the percentages expressing oak, linden, and maple seeds from that 100%. This will tell us how many percent are acacia seeds:
100% − (60% + 15% + 20%) = 100% − 95% = 5%
Now we find the acacia seeds:
60 × 0.05 = 3 kg
Answer: the students collected 3 kg of acacia seeds.
Check:
60 × 0.60 = 36
60 × 0.15 = 9
60 × 0.20 = 12
60 × 0.05 = 3
36 + 9 + 12 + 3 = 60
60 = 60
Task 8. A man bought groceries. The meat costs $60, which is 48% of the cost of all purchases. Determine the total amount of money spent on groceries.
Solution
This is a task of finding a number by its percentage, i.e. by its known part. Such a task can be solved in two ways. The first is to express the known number of percentages as a decimal fraction and find the unknown number using the fraction
Express 48% as a decimal
48% : 100 = 0.48
Knowing that $0.48 is $60, we can determine the amount of all purchases. To do this, find the unknown number on the decimal:
60 : 0.48 = $125.
So, the total amount of money spent on groceries is $125.
The second way is to find out how much money is in one percent, and then multiply the result by 100.
48% is $60. If we divide $60 by 48, we find out how many dollars are in the 1%
60: 48% = $1.25.
The 1% is $1.25. That's a total of 100 percent. If we multiply $1.25 by 100, we get the total amount of money spent on groceries
1.25 × 100 = $125
Task 9. 35% of the fresh plums are dried. How many fresh plums must be taken in order to get 140 kg of dried plums? How many dried plums will you get from 600 kg of fresh plums?
Solution
Express 35% as a decimal fraction and find the unknown number in the fraction:
35% = 0.35
140 : 0.35 = 400 kg
In order to get 140 kg of dried plums, we have to take 400 kg of fresh plums.
Let's answer the second question: how many dried plums do we get from 600 kg of fresh plums? If fresh plums yield 35% of dried plums, it is sufficient to find this 35% of 600 kg of fresh plums
600 × 0,35 = 210 kg
Answer: to get 140 kg of dried plums you should take 400 kg of fresh plums. From 600 kg of fresh plums you will get 210 kg of dried plums.
Task 10. The absorption of fats by the human body is 95%. In one month the student consumed 1.2 kg of fats. How much fat can be absorbed by his body?
Solution
Let's convert 1.2 kg to grams
1.2 × 1000 = 1200 g
Find 95% of 1200 g
1200 × 0.95 = 1140 g
Answer: 1140 g of fats can be absorbed by the student's body.
Expressing numbers as percentages
Percentages, as mentioned earlier, can be represented as decimals. To do this, simply divide the number of these percentages by 100. For example, let's represent 12% as a decimal:
![]()
Note. We don't find the percentage of something now, we just write it down as a decimal.
But the reverse process is also possible. A decimal can be represented as a percentage. To do this, multiply the decimal fraction by 100 and put the percent sign (%).
Let's represent the decimal 0.12 as a percentage
0.12 × 100 = 12%
This action is called expressing a number in percentages or expressing numbers in hundredths.
Multiplication and division are inverse operations. For example, if 2 × 5 = 10, then 10 : 5 = 2
Similarly, division can be written in reverse order. If 10 : 5 = 2, then 2 × 5 = 10:

The same thing happens when we express a decimal as a percentage. So, 12% was expressed as a decimal as follows: 12 : 100 = 0.12 but then that same 12% was "returned" by multiplication, writing the expression 0.12 × 100 = 12%.
Similarly, any other numbers, including integers, can be expressed as a percentage. For example, express the number 3 as a percentage. Multiply this number by 100 and add a percent sign to the result:
3 × 100 = 300%
Large percentages like 300% can be confusing at first, because people are used to thinking of 100% as the maximum. From additional information about decimals, we know that one whole object can be denoted by one. For example, if there is a whole uncut cake, it can be represented as 1
The same cake can be denoted as 100% cake. In this case, both one and 100% will denote the same whole cake:

Cut the cake in half. In this case, one will convert to the decimal 0.5 (because it is half of one), and 100% will convert to 50% (because 50 is half of a hundred)
Let's bring back a whole cake, one and 100%

Let's picture two more of these cakes with the same designations:
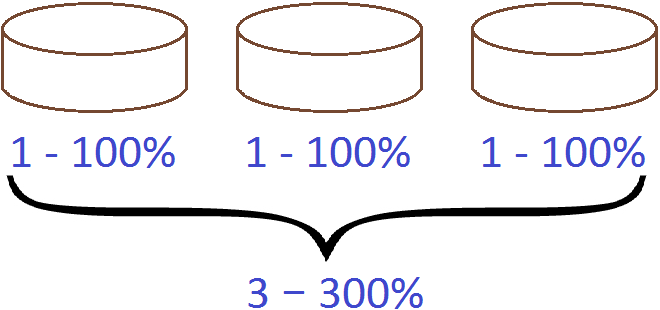
If one cake is a unit, three cakes are three units. Each cake is a hundred percent whole. If you add up those three hundreds you get 300%.
Therefore, when converting whole numbers to percentages, we multiply these numbers by 100.
Task 2. Express 5 as a percentage
5 × 100 = 500%
Task 3. Express 7 as a percentage
7 × 100 = 700%
Task 4. Express 7.5 as a percentage
7.5 × 100 = 750%
Task 5. Express 0.5 as a percentage
0.5 × 100 = 50%
Task 6. Express 0.9 as a percentage
0.9 × 100 = 90%
Task 7. Express 1.5 as a percentage
1.5 × 100 = 150%
Task 8. Express 2.8 as a percentage
2.8 × 100 = 280%
Task 9. George walks home from school. For the first fifteen minutes he walked 0.75 of the way. The rest of the time, he walked the remaining 0.25 of the way. Express in percentages the parts of the path George walked.
Solution
0.75 × 100 = 75%
0.25 × 100 = 25%
Task 10. John was given half of an apple. Express this half as a percentage.
Solution
Half of an apple is written as a decimal 0.5. To express this decimal as a percentage, multiply it by 100 and add a percent sign to the result
0.5 × 100 = 50%
Fractional equivalents
A value expressed as a percentage has its counterpart in the form of an ordinary fraction. For example, the analogue for 50% is a fraction of ![]() . Fifty percent can also be called "half".
. Fifty percent can also be called "half".
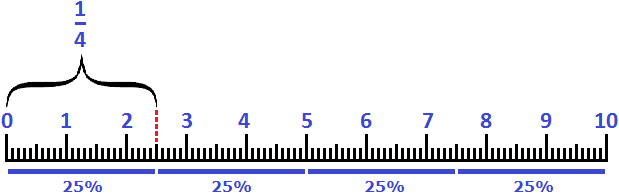
The analogy for 25% is the fraction ![]() . Twenty-five percent can also be called the word "quarter".
. Twenty-five percent can also be called the word "quarter".
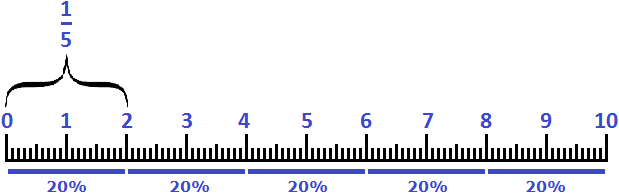
The analogy for 20% is the fraction ![]() . Twenty percent can also be referred to by the words "one-fifth".
. Twenty percent can also be referred to by the words "one-fifth".
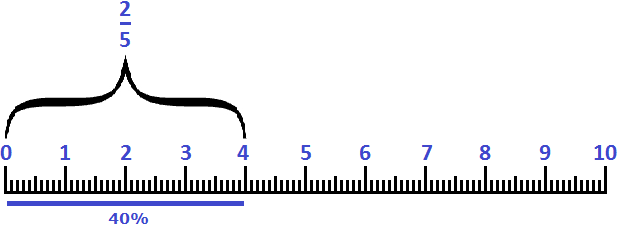
The analogue for 40% is the fraction ![]() .
.
The analogue for 60% is the fraction ![]() .
.
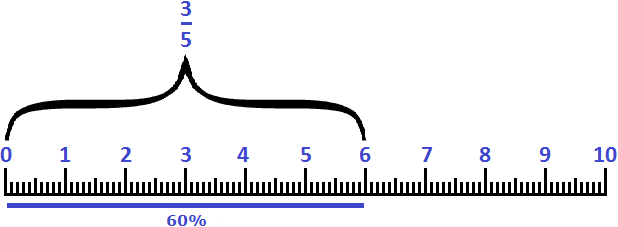
Example 1. Five centimeters is 50% of a decimeter or ![]() or just half. In all cases we are talking about the same value, five centimeters out of ten
or just half. In all cases we are talking about the same value, five centimeters out of ten

Example 2. Two and a half centimeters is 25% of a decimeter or ![]() or just a quarter
or just a quarter
Example 3. Two centimeters is 20% of a decimeter or ![]()
Example 4. Four centimeters is 40% of a decimeter or ![]()
Example 5. Six centimeters is 60% of a decimeter or ![]()
Decreasing and increasing values
Examples:
- To increase by 50% means to increase the value by 1.5 times;
- To increase by 100% - means to increase the value by 2 times;
- To increase by 200% means to increase the value by 3 times;
- To reduce by 50% - means to reduce the value by 2 times;
- To reduce by 80% means to reduce the value by 5 times;
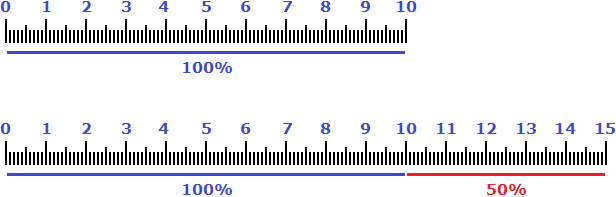
Example 1. Ten centimeters was increased by 50%. How many centimeters did you get?
To solve such problems, you must take the initial value as 100%. The initial value is 10 cm. 50% of it is 5 cm.
The original 10 centimeters were maximized by 50% (5 centimeters), so we got 10+5 centimeters, which is 15 centimeters.
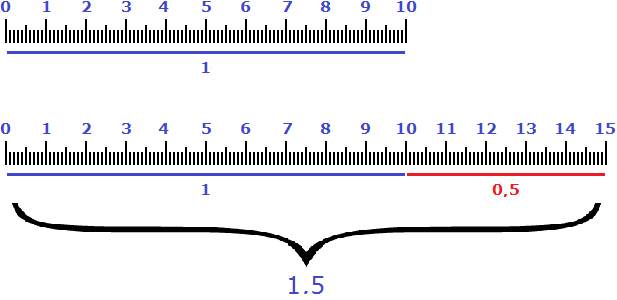
The equivalent of increasing ten centimeters by 50% is a multiplier of 1.5. If you multiply ten centimeters by it, you get 15 centimeters.
10 × 1.5 = 15 cm
Therefore, the expressions "increase by 50%" and "increase by 1.5 times" mean the same thing.
Example 2. Five centimeters were increased by 100%. How many centimeters did you get?
Let's take the original five centimeters as 100%. One hundred percent of those five centimeters would be 5 centimeters themselves. If you increase 5 centimeters by the same 5 centimeters, you get 10 centimeters.
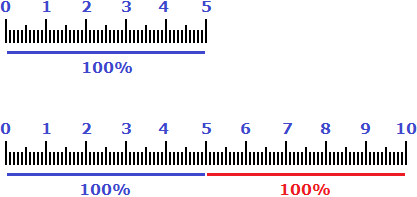
The equivalent of increasing five centimeters by 100% is a multiplier of 2. If you multiply five centimeters by it, you get 10 centimeters.
5 × 2 = 10 cm

Therefore, the expressions "increase by 100%" and "increase by 2 times" mean the same thing.
Example 3. Five centimeters were increased by 200%. How many centimeters did you get?
Take the original five centimeters as 100%. Two hundred percent is two times one hundred percent. That is, 200% of 5 centimeters would be 10 centimeters (5 centimeters for every 100%). If you increase 5 cm by that 10 cm, you get 15 cm.
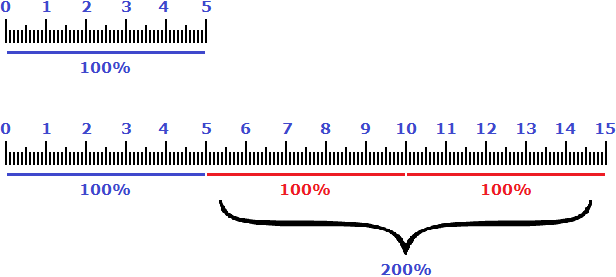
The equivalent of increasing five centimeters by 200% is a multiplier of 3. If you multiply five centimeters by it, you get 15 centimeters.
5 × 3 = 15 cm
Therefore, the expressions "increase by 200%" and "increase by 3 times" mean the same thing.
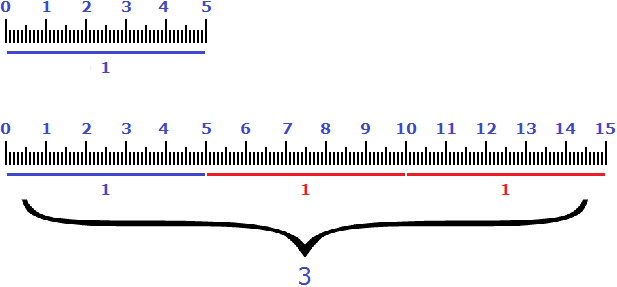
Example 4. Ten centimeters were reduced by 50%. How many centimeters are left?
Let's take the original 10 cm as 100%. Fifty percent of 10 cm is 5 cm. If you reduce 10 centimeters by that 5 centimeters, 5 centimeters remain.
Analogous to the reduction of ten centimeters by 50% is the divisor 2. If you divide 10 cm by it, you get 5 cm
10 : 2 = 5 cm
Therefore, the expressions "reduce by 50%" and "reduce by half" mean the same thing.
Example 5. Ten centimeters were reduced by 80%. How many centimeters are left?
Take the original 10 cm as 100%. Eighty percent of 10 cm is 8 cm. If you reduce 10 centimeters by that 8 centimeters, 2 centimeters remain.
Analogous to the reduction of ten centimeters by 80% is the divisor 5. If you divide 10 cm by it, you get 2 cm
10 : 5 = 2 cm
Therefore, the expressions "decrease by 80%" and "decrease by a factor of 5" say the same thing.
When solving tasks for decreasing and increasing percentages, you can multiply/divide the value by the multiplier specified in the task.
Task 1. How much did the value change if it increased by a factor of 1.5?
The value in the problem can be written as 100%. Then multiply 100% by a factor of 1.5.
100% × 1.5 = 150%
Now subtract the original 100% from 150% and get the answer to the problem:
150% − 100% = 50%
Task 2. How much percent has the value changed if it has decreased by a factor of 4?
This time the value will decrease, so we will do division. Let's call the value mentioned in the problem 100%. Then divide 100% by the divisor 4.
100% : 4 = 25%
Let's subtract the resulting 25% from the original 100% and get the answer to the problem:
100% − 25% = 75%
This means that when the value is decreased by a factor of 4, it has decreased by 75%.
Task 3. How much did the value change if it decreased by a factor of 5?
Let's denote the value of the problem as 100%. Then divide this 100% by the divisor of 5.
100% : 5 = 20%
Deduct the resulting 20% from the original 100% and get the answer to the problem:
100% − 20% = 80%
This means that when the value is decreased by a factor of 5, it is decreased by 80%.
Task 4. How much did the value change if it decreased by a factor of 10?
Let's denote the value of the problem as 100%. Then divide this 100% by the divisor of 10.
100% : 10 = 10%
From the original 100% subtract the resulting 10% and get the answer to the problem:
100% − 10% = 90%
This means that when the value is reduced by a factor of 10, it is reduced by 90%.
How to find the percentage
To express something as a percentage, first write down a fraction showing how much the first number is a fraction of the second number, then divide it into fractions and express the result as a percentage.
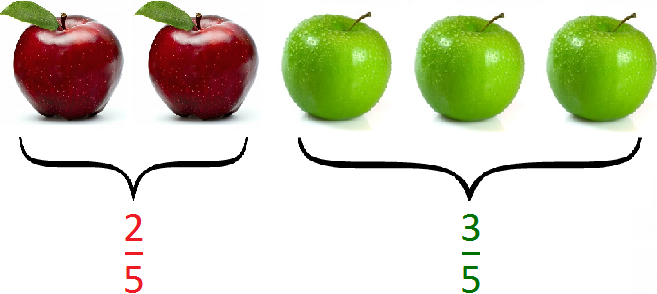
For example, let there be five apples. Two apples are red and three are green. Express the red and the green apples as a percentage.
First we need to find out what fraction of the red apples are. There are five apples in all and two red apples. So two out of five, or two-fifths, are red apples:

The green apples, on the other hand, are three. So three out of five, or three-fifths, are green apples:
We have two fractions ![]() and
and ![]() . Perform division in these fractions
. Perform division in these fractions
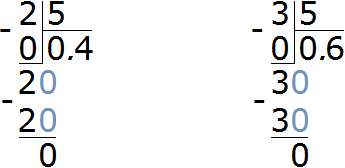
We obtained the decimals 0.4 and 0.6. Now express these decimals as a percentage:
0.4 × 100 = 40%
0.6 × 100 = 60%
So 40% are red apples and 60% are green apples.
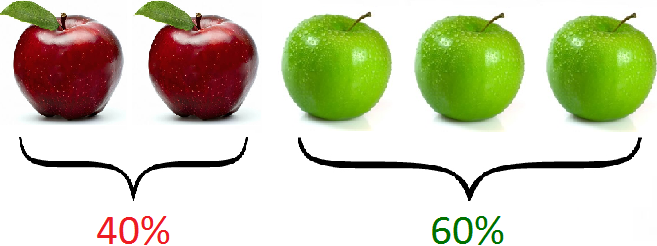
And all five apples are 40%+60%, i.e. 100%
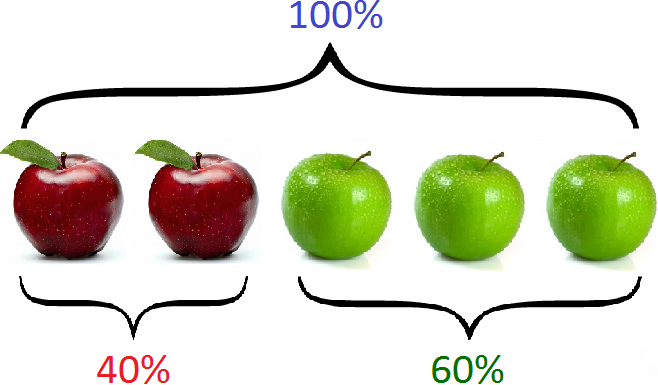
Task 2. Two sons were given $200 by their mother. The younger brother was given $80 by his mother and the older brother $120. Express as a percentage the money given to each brother.
Solution
The younger brother received eighty dollars out of $200. Write down a fraction of eighty-two hundred:
![]()
The older brother got $120 out of $200. Record a fraction of one hundred and twenty-two hundred:
![]()
We have fractions ![]() and
and ![]() . Perform division in these fractions
. Perform division in these fractions

Let's express the results as a percentage:
0.4 × 100 = 40%
0.6 × 100 = 60%
So 40% of the money went to the younger brother and 60% to the older brother.
So the fractions ![]() and
and ![]() could be reduced. This would not change the answer to the problem:
could be reduced. This would not change the answer to the problem:
Task 3. A rich family has a budget of $75,000 per month. Of that, $52,500 is money earned by Dad. $22,500 is money earned by mom. Express in percentages the money earned by Dad and Mom.
Solution
You should express in percentages the money earned by Dad. He earned $52,500 out of $75,000.
![]()
Let's perform division in this fraction:
![]()
Let's express the result as a percentage:
0.7 × 100 = 70%
So Dad earned 70% of the money. Then it's easy to guess that Mom made the other 30% of the money. After all, $75,000 is 100% of the money. To be sure, let's check. Mom earned $22,500 out of $75,000 Write down the fraction, do the division, and express the result as a percentage:
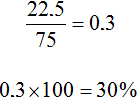
Task 4. A student is training to do pull-ups on the bar. Last month he could do 8 pull-ups in an attempt. This month he can do 10 pull-ups in an attempt. By how many percent has he increased his number of pull-ups?
Solution
Let's see how many more pull-ups a student does this month than last month
10 − 8 = 2
Let's find out what part two pull-ups make of eight pull-ups. To do this, find the ratio of 2 to 8
![]()
Perform division in this fraction
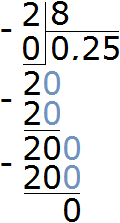
Let's express the result as a percentage:
0.25 × 100 = 25%
So, the student increased the number of pull-ups by 25%.
This task can also be solved by the second, faster method - find out how many times 10 pull-ups are more than 8 pull-ups and express the result as a percentage.
To find out how many times ten pull-ups are more than eight pull-ups, find the ratio of 10 to 8
![]()
Perform division in the resulting fraction
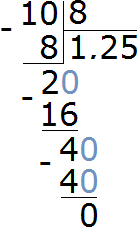
Let's express the result as a percentage:
1.25 × 100 = 125%
This month's pull-up rate is 125%. This statement should be understood to mean "is 125%", not "is 125% higher". These are two different statements expressing different quantities.
The statement "is 125%" should be understood as "eight pull-ups, which are 100% plus two pull-ups, which are 25% of eight pull-ups". Graphically, this looks as follows:
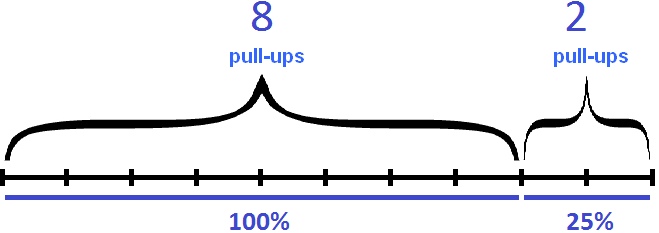
And the statement "increased by 125%" should be understood as "to the current eight pull-ups, which were 100% added another 100% (8 more pull-ups) plus another 25% (2 more pull-ups)". The total is 18 pull-ups
100% + 100% + 25% = 8 + 8 + 2 = 18 pull-up
Graphically, this statement is as follows:
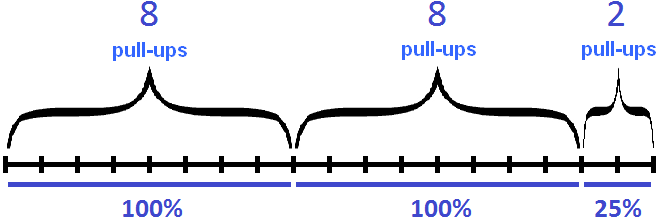
That's a total of 225%. If we find 225% of eight pull-ups, we get 18 pull-ups
8 × 2.25 = 18
Task 5. Last month the director's salary was $19,200. This month it is $20,160. How much has the salary increased by?
This task, like the previous one, can be solved in two ways. The first is to first find out how many dollars the salary has increased. Next, find out how much of the raise is from the previous month's salary
Find out how many dollars were raised:
20.16 - 19.2 = $0.96 thousand.
Let's find out what part of $0.96 is from $19.2. To do this, find the ratio of 0.96 to 19.2
![]()
Let's perform division in the resulting fraction. At the same time, let's remember how to divide decimals:
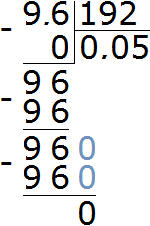
Let's express the result as a percentage:
0.05 × 100 = 5%
This means that the wage increased by 5%.
Let's solve the problem in the second way. Let's find out how many times $20.16 thousand is more than $19.2 thousand To do this, find the ratio of $20.16 to $19.2
![]()
Perform division in the resulting fraction:
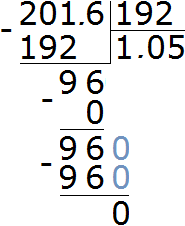
Let's express the result as a percentage:
1.05 × 100 = 105%
The salary is 105%. So this includes 100%, which was $19200, plus 5%, which is $0.96 K
100% + 5% = 19.2 + 0.96
Task 6. The price of a top-of-the-line notebook computer went up 5% this month. What is its price if it cost $18300 last month?
Solution
Let's find 5% of 18.3:
18.3 × 0.05 = 0.915
Let's add this 5% to 18.3:
18.3 + 0.915 = $19.215.
Answer: The price of the laptop is $19215.
Task 7. The price of a top-of-the-line notebook computer decreased by 10% this month. What is its price if it cost $16,300 last month?
Solution
Let's find 10% of 16.3:
16.3 × 0.10 = 1.63
Let's subtract this 10% from 16.3:
16.3 - 1.63 = $14.67 (thousand dollars)
Similar problems can be written in brief:
16.3 - (16.3 × 0.10) = $14.67 (thousand dollars)
Answer: the price of the laptop is 14.67 thousand dollars.
Task 8. Last month, the price of a top-of-the-line laptop was $21,000. This month the price went up to $22,050. By how much did the price go up?
Solution
Let's determine how much the price has gone up
22.05 - 21 = 1.05 (thousand dollars)
Let's find out what part of $1.05 thousand is from $21 thousand.
![]()
Let's express the result as a percentage
0.05 × 100 = 5%
Answer: the price of the laptop increased by 5%.
Task 8. A worker was supposed to make 600 parts according to the plan, but he made 900 parts. How many percent did he meet the plan?
Solution
Find out how many times 900 parts are more than 600 parts. To do this, find the ratio of 900 to 600
![]()
The value of this fraction is 1.5. Express this value as a percentage:
1.5 × 100 = 150%
So, the worker fulfilled the plan by 150%. That is, he fulfilled it by 100%, making 600 parts. Then he produced another 300 parts, which is 50% of the original plan.
Answer: The worker fulfilled the plan by 150%.
Comparison of values in percentages
We have already compared magnitudes many times in different ways. Our first tool was the division. So, for example, to compare $5 and $3, we wrote down the divison 5-3. By getting an answer of 2, we could say that "five dollars is two dollars more than three dollars".
Thus, the difference between five dollars and three dollars is two dollars.
The next tool we used to compare values was ratio. The ratio allowed us to find out how many times the first number is greater than the second number (or how many times the first number contains the second number).
So, for example, ten apples are five times the size of two apples. Or to put it another way, ten apples contains two apples five times. This comparison can be written using the ratio
![]()
But values can also be compared in percentages. For example, compare the price of two goods not in dollars, but estimate how much the price of one good is more or less than the price of the other as a percentage.
To compare values as a percentage, one of them should be marked as 100%, and the second one, based on the conditions of the task.
For example, let's find out by how many percent ten apples are more than eight apples.
For 100% you should write the value to which you are comparing something. We are comparing ten apples with eight apples. So for 100% we give 8 apples:

Now our task is to compare how many percent more 10 apples are than these 8 apples. 10 apples is 8+2 apples. So by adding two more apples to the eight apples, we increase 100% by another number of percent. To find out how many percent of the eight apples are two apples
![]()
Adding this 25% to the eight apples, we get 10 apples. And 10 apples is 8+2, that is 100% and another 25%. So that's 125%.

So ten apples are 25% more than eight apples.
Now solve the inverse problem. Let's find out how much less eight apples are than ten apples. The immediate answer is that eight apples are 25% less than ten apples. However, this is not true.
We are comparing eight apples to ten apples. We agreed that we would take as 100% what we are comparing with. So this time we take ten apples as 100%:

Eight apples are 10-2, that is, if we decrease 10 apples by 2 apples, we decrease them by some number of percent. To find out how many percent of the ten apples are two apples
![]()
By subtracting that 20% from ten apples, we get eight apples. And 8 apples is 10-2, which is 100% minus 20%. So that's 80%.
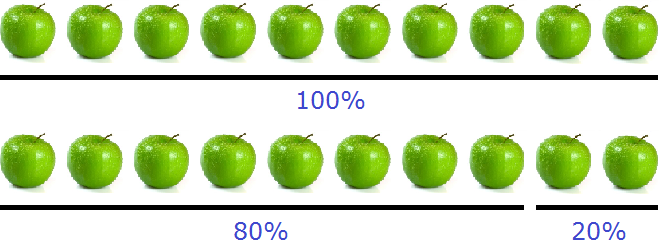
So eight apples is 20% less than ten apples.
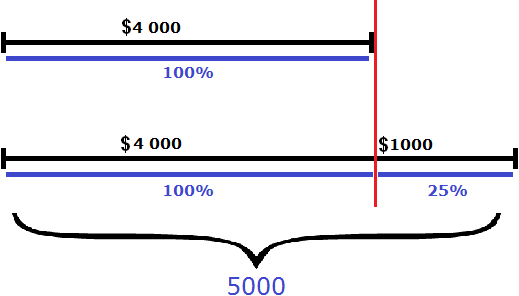
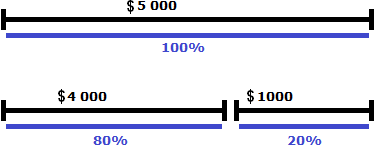
Task 2. By how much is $5,000 more than $4,000?
Solution
Let's take $4,000 as 100%. Five thousand is more than four thousand by one thousand. So if we increase four thousand by one thousand, we increase four thousand by some number of percent. Let's find out how much. To do this, let's determine how much one thousand is a fraction of four thousand:
![]()
Let's express the result as a percentage:
0.25 × 100 = 25%
$1,000 of $4,000 is 25%. If you add that 25% to $4,000, you get $5,000. So $5,000 is 25% more than $4,000.
Task 3. By how much percent is $4,000 less than $5,000?
This time we compare $4,000 to $5,000. Let's take 5,000 as 100%. Five thousand is more than four thousand dollars by one thousand dollars. Find out what fraction of one thousand is from five thousand
![]()
One thousand from five thousand is 20%. If you subtract that 20% from $5,000, you get $4,000.
So $4,000 is less than $5,000 by 20%.
Alloy mixture problem
Let's say we want to make some juice. We have water and raspberry syrup

Pour 200 ml of water into a glass:

Add 50 ml of raspberry syrup and stir the resulting liquid. The result will be 250 ml of raspberry juice (200 ml of water + 50 ml of syrup = 250 ml of juice).
How much of the resulting juice is raspberry syrup?
The raspberry syrup is ![]() juice. Let's calculate this ratio and get the number 0.20. This number shows the amount of dissolved syrup in the resulting juice. Let's call this number the syrup concentration.
juice. Let's calculate this ratio and get the number 0.20. This number shows the amount of dissolved syrup in the resulting juice. Let's call this number the syrup concentration.
The concentration of a dissolved substance is the ratio of the amount of a dissolved substance or its mass to the volume of mixture.
Concentration is usually expressed as a percentage. Let's express the syrup concentration as a percentage:
0.20 × 100 = 20%
Thus, the concentration of syrup in the raspberry juice is 20%.
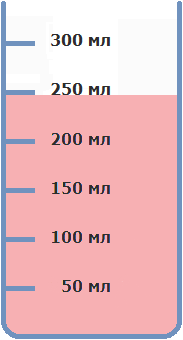
The substances in the mixture can be heterogeneous. For example, let's mix 3 liters of water and 200 g of salt.
The mass of 1 liter of water is 1 kg. Then the mass of 3 liters of water will be 3 kg. Let's convert 3 kg to grams, so we have 3 kg = 3000 g.
Now let's add 200 g of salt to 3000 g of water and mix the resulting liquid. The result will be a salt mixture, the total mass of which will be 3000+200, i.e. 3200 g. Let's find the concentration of salt in the resulting mixture. To do this, find the ratio of the mass of the dissolved salt to the mass of the solution
![]()
So, mixing 3 liters of water and 200 g of salt will produce a 6.25% salt mixture.
Similarly, the amount of a substance in an alloy or in a mixture can be determined. For example, an alloy contains 210 g of tin and 90 g of silver. Then the mass of the alloy will be 210+90, i.e. 300 g. The alloy would contain ![]() tin, and
tin, and ![]() silver. The percentage of tin will be 70% and silver 30%.
silver. The percentage of tin will be 70% and silver 30%.
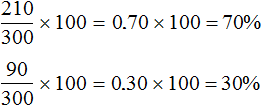
When two solutions are mixed, a new solution is obtained, consisting of the first and second solutions. The new mixture may have a different concentration of a substance. It is a useful skill to be able to solve concentration, alloys, and mixture problems. In general, the point of such problems is to keep track of the changes that occur when mixtures of different concentrations are mixed.
Let's mix two raspberry juices. The first juice of 250 ml contains 12.8% raspberry syrup. And the second juice of 300 ml contains 15% raspberry syrup. Pour these two juices into a large glass and mix. The result is a new juice with a volume of 550 ml.
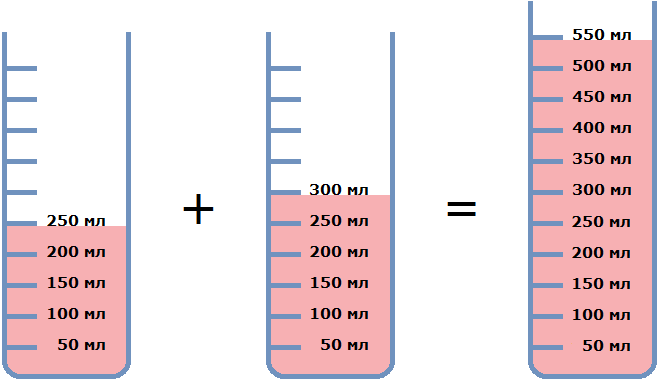
Now let's determine the concentration of syrup in the resulting juice. The first drained juice of 250 ml contained 12.8% syrup. And 12.8% of 250 ml is 32 ml. This means that the first juice contained 32 ml of syrup.
The second drained juice of 300 ml contained 15% syrup. And 15% of 300 ml is 45 ml. So the second juice contained 45 ml of syrup.
Let's add up the amounts of syrup:
32 ml + 45 ml = 77 ml
This 77 ml of syrup is contained in the new juice, which has a volume of 550 ml. Determine the concentration of syrup in this juice. To do this, find the ratio of 77 ml of dissolved syrup to the volume of juice 550 ml:
![]()
So mixing 12.8% raspberry juice with 250 ml and 15% raspberry juice with 300 ml produces 14% raspberry juice with 550 ml.
Task 1. There are three mixtures of sea salt in water: the first mixture contains 10% salt, the second mixture contains 15% salt, and the third mixture contains 20% salt. Mix 130 ml of the first solution, 200 ml of the second mixture, and 170 ml of the third mixture. Determine how much of the sea salt is in the resulting mixture.
Solution
Determine the volume of the resulting mixture:
130 ml + 200 ml + 170 ml = 500 ml
Since the first mixture had 130 × 0.10 = 13 ml of sea salt, the second mixture had 200 × 0.15 = 30 ml of sea salt, and the third mixture had 170 × 0.20 = 34 ml of sea salt, the resulting mixture will contain 13 + 30 + 34 = 77 ml of sea salt.
Determine the concentration of sea salt in the resulting mixture. To do this, find the ratio of 77 ml of sea salt to the volume of the mixture of 500 ml
![]()
So, the resulting solution contains 15.4% sea salt.
Task 2. How many grams of water must be added to 50 g of a mixture containing 8% salt to get a 5% mixture?
Solution
Note that if you add water to the existingmixture, the amount of salt in it will not change. Only the percentage of salt will change because adding water to the mixture will change its mass.
We need to add such an amount of water that eight percent of the salt becomes five percent.
Let's find how many grams of salt are in 50 grams of mixture. To do this, find eight percent of 50
50 g × 0.08 = 4 g
Eight percent of 50 grams is 4 grams. In other words, there are four grams of salt for eight parts out of a hundred. Let's make it so that these 4 grams are not eight parts, but five parts, that is, 5%
4 grams - 5%
Now knowing that there are 4 grams per 5% of the mixture, we can find the mass of the entire mixture. To do this, we need to find the number by its percentage:
4 g : 5 = 0.8 g
0.8 g × 100 = 80 g
80 grams of mixture is the mass at which 4 grams of salt will account for 5% of the mixture. And to get this 80 grams, you need to add 30 grams of water to the original 50 grams.
So, to get a 5% mixture of salt, you need to add 30 grams of water to the mixture you have.
Task 2. Grapes contain 91% moisture and raisins contain 7%. How many kilograms of grapes are required to produce 21 kilograms of raisins?
Solution
Grapes consist of moisture and pure matter. If fresh grapes contain 91% moisture, the remaining 9% will be the pure matter of those grapes:

Raisins, on the other hand, contain 93% pure matter and 7% moisture:

Note that in the process of turning grapes into raisins, only the moisture of those grapes disappears. The pure substance remains unchanged. After the grapes are turned into raisins, the resulting raisin has 7% moisture and 93% pure matter.
Let's determine how much pure matter is in 21 kg of raisins. To do this we find 93% of 21 kg
21 kg × 0.93 = 19.53 kg
Now let's go back to the first figure. Our task was to determine how many grapes we need to take to produce 21 kg of raisins. The net weight of 19.53 kg would be 9% of the grapes:
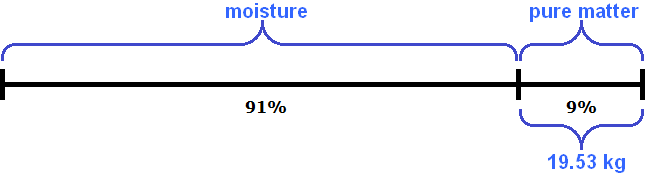
Now knowing that 9% pure matter is 19.53 kg, we can determine how many grapes it takes to get 21 kg of raisins. To do this we need to find the number by its percentage:
19.53 kg : 9 = 2.17 kg
2.17 kg × 100 = 217 kg
So, to get 21 kg of raisins you need to take 217 kg of grapes.
Task 3. An alloy of tin and copper contains 85% copper. How much alloy should be taken so that it contains 4.5 kg of tin?
Solution
If the alloy contains 85% copper, the remaining 15% will be tin:

The question is how much alloy should be taken to contain 4.5 kg of tin. Since the alloy contains 15% tin, then 4.5 kg of tin will account for this 15%.
And knowing that 4.5 kg of alloy is 15%, we can determine the mass of the entire alloy. To do this, we need to find the number by its percentage:
4.5 kg : 15 = 0.3 kg
0.3 kg × 100 = 30 kg
So, the alloy must be taken 30 kg, so that it contains 4.5 kg of tin.
Task 4. Mix some amount of 12% hydrochloric acid solution with the same amount of 20% solution of the same acid. Find the concentration of the resulting hydrochloric acid.
Solution
Let's plot the first solution as a straight line and plot the 12%

Since the number of solutions is the same, the same figure can be shown next to it, illustrating the second solution with 20% hydrochloric acid.

We got two hundred parts of the solution (100% + 100%), thirty-two parts of which is hydrochloric acid (12% + 20%).
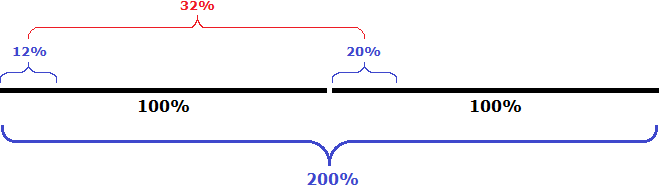
Determine how much of the 32 parts make up the 200 parts
![]()
So, mixing a 12% hydrochloric acid solution with the same amount of a 20% solution of the same acid will produce a 16% hydrochloric acid solution.
To check, imagine that the mass of the first solution was 2 kg. The mass of the second solution will also be 2 kg. Then, when these solutions are mixed, we will get 4 kg of solution. The first solution of hydrochloric acid had 2 × 0.12 = 0.24 kg, and the second solution had 2 × 0.20 = 0.40 kg. Then the new solution of hydrochloric acid will have 0.24 + 0.40 = 0.64 kg. The concentration of hydrochloric acid will be 16%
![]()
Exercises
Solution
Let's find 20% of 50
50 × 0.20 = 10
Add the resulting number 10 to the number 50, we get a new value of 60
50 + 10 = 60
Answer: the new value is 60.
Solution
Find 60% of ![]() and add them to
and add them to ![]() . This is how we determine the new value of the number.
. This is how we determine the new value of the number.
For the convenience of finding sixty percent of ![]() , replace 60% with its counterpart in the form of an fraction
, replace 60% with its counterpart in the form of an fraction ![]() . By multiplying
. By multiplying ![]() by
by ![]() , we will find 60% of the number
, we will find 60% of the number ![]()
![]()
Now increase the number ![]() by the found 60%, i.e. by the number
by the found 60%, i.e. by the number ![]()
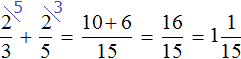
Answer: the new value is equal to ![]()
Task 12. Answer the following questions:
1) 80 percent of money were spent. How much of that amount is left over?
2) Men are 75% of all workers in the plant. How many percent of the workers in the plant are women?
3) Girls make up 40% of the class. How many percent of the class are boys?
Answers
1) 20%
2) 25%
3) 60%
Task 13. Answer the following questions:
1) The store received 2500 kg of tomatoes. On the first day, 30% of all tomatoes were sold. How many kilograms of tomatoes are left to sell?
2) The school has 400 students, 52% of that number are girls. How many boys are there in the school?
Answers:
1) 1750;
2) 192.
Solution
Let's use a variable. Let A be the initial number in the task. Take this initial number A as 100%

Let's increase this initial number A by 25%

Now the new number is 125%. Let's find out what part of 125% is 25%. To do this, find the ratio of 25% to 125%
![]()
Let's express the result as a percentage:
0.2 × 100 = 20%

Answer: To get the original number, the new number must be reduced by 20%.
Solution
Let's use a variable. Let P be the initial number in the task. Take this initial number P as 100%
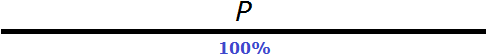
Reduce this initial number P by 50%

Now the new number is 50% of the original number. Find out how many times the original number P is greater than the new number. To do this, find the ratio of 100% to 50%
![]()
The original number is twice as big as the new number. You can see this even in the picture. And to make the new number equal to the original number, it must be doubled. And doubling the number means increasing it by 100%.
So the new number, which is half of the original number, must be increased by 100%.
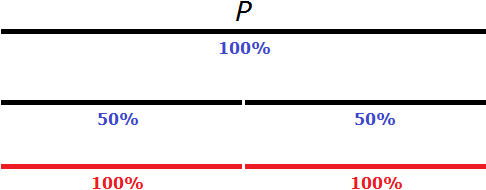
Considering the new number, it is also taken as 100%. For example, in the figure above, the new number is half of the original number and is signed as 50%. In relation to the original number, the new number is half. But if you consider it separately from the original number, it should be taken as 100%.
Therefore, in the figure, the new number that is represented by the line was first designated as 50%. But then we labeled this number as 100%.
Answer: To get the original number, the new number must be increased by 100%.
This month, the number is down to 6. By how many percent did the number of accidents decrease?
Solution
Last month there were 15 accidents. This month there are six. So the number of accidents is down by 9.
Let's take 15 accidents as 100%. By reducing the 15 accidents by 9, we will reduce them by some number of percent. To find out what percentage, let's find out what portion of the 9 accidents are from the 15 accidents
![]()
9 accidents from 15 is 60%. So the number of accidents decreased by 60%.
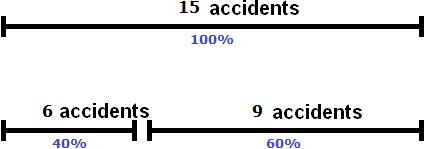
Answer: The number of accidents decreased by 60%.
Solution
Let us add up the masses of the initial solutions:
8 kg + 12 kg = 20 kg
The first solution had 8 × 0.18 = 1.44kg of substance, and the second solution had 12 × 0.08 = 0.96kg of the same substance. Then the resulting solution will contain 1.44 + 0.96 = 2.40 kg.
Determine the concentration of the substance in the resulting solution:
![]()
Answer: the concentration of the resulting solution is 12%.
Solution
The mass of both solutions is the same. Each solution can be taken as 100%. After adding the solutions, you will get 200% of the solution. The first solution had 11% of the substance and the second solution had 19% of the substance. Then the resulting 200% solution will have 11% + 19% = 30% of the substance.

Let us determine the concentration of the resulting solution. To do this, find out what part of the thirty parts of the substance is from two hundred parts of the substance:
![]()
Answer: the concentration of the resulting solution is 15%.
Solution
Introduce the original price of the food as 100%. For the convenience of solving the problem, we will express the percentages as decimals. Then 100% as a decimal will be written as 1.
The price increased by 10% in the first month. Add ten percent of that price to the existing price of 1, you get 1 + 0.10 × 1. That amount is equal to the expression 1.10. So the price for the first month will be 1.10.
In the second month, the price has also increased by 10 percent. Add ten percent of that price to the current price of 1.10, you get 1.10 + 0.10 × 1.10. This amount equals the expression 1.21. So the price for the second month will be 1.21.
In the third month, the price has also increased by 10%. Add ten percent of that price to the current price of 1.21, you get 1.21 + 0.10 × 1.21. This amount equals the expression 1.331. Then the price for the third month will be 1.331.
Calculate the difference between the new price and the old price. If the original price was 1, then the price has risen by 1.331 - 1 = 0.331. Express the result as a percentage, so we obtain 0.331 × 100 = 33.1%.
Answer: in three months, food prices increased by 33.1%.





Comments
Thanks for finding the bug! All fixed!
I found 2 type error, Task 8 is 22,050 not 22,500. Task 5 is 20,160 not 20,600