In this lesson we will learn about multiplication and division of rational numbers.
How to multiply rational numbers
The rules for multiplying integers are also true for rational numbers. In other words, to multiply rational numbers, you must be able to multiply integers.
It is also necessary to know the basic laws of multiplication such as the commutative law of multiplication, the associative law of multiplication, the distributive law of multiplication, and the law of multiplication by zero.
Example 1. Find the value of the expression 
This is multiplication of rational numbers with different signs. To multiply rational numbers with different signs, multiply their modules and put minus sign in front of the result.
To clearly see that we are dealing with numbers with different signs, put each rational number in parentheses along with its signs
The modulus of 
is 
, and the modulus of 
is . By multiplying these modules as positive fractions, we obtained the answer 
, but in front of the answer we put a minus sign. To provide this minus before the result, the multiplication of modules was performed in parentheses, and the minus was put in front of the result.
Thus, the value of the expression is 
The short solution is as follows:
Example 2. Find the value of the expression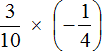 
This is a multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer:
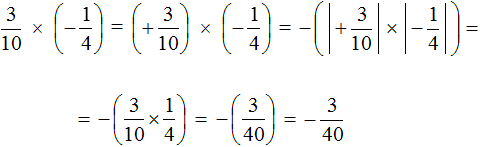
The solution for this example can be written in a shorter form:
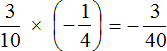
Example 3. Find the value of the expression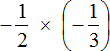 
This is multiplication of negative rational numbers. To multiply negative rational numbers, multiply their modules and put plus sign in front of the answer
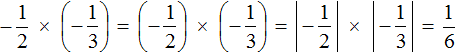
The solution for this example can be written in a shorter form:
Example 4. Find the value of the expression 
This is a multiplication of negative rational numbers. Multiply the modules of these numbers and put plus in front of the answer
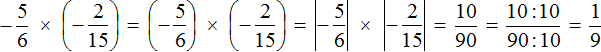
The solution for this example can be written in a shorter form:
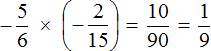
Example 5. Find the value of the expression 
This is a multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer
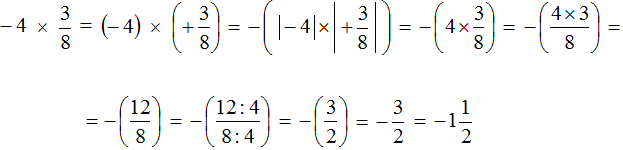
A short solution would look much easier:
Example 6. Find the value of the expression 
Let's convert the mixed number 
to an improper fraction. Let's rewrite the rest as it is
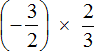
We obtained the multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer. You can skip the entry with modules, so as not to overload the expression
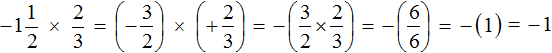
The solution for this example can be written in shorter form
Example 7. Find the value of the expression 
This is a multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer
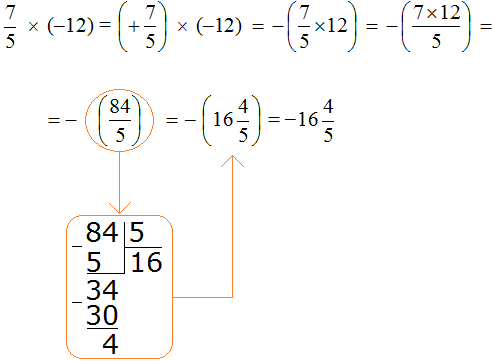
At first, the answer was an improper fraction 
, but we extracted the whole part of it. Note that the whole part was extracted from the modulus of the fraction . The resulting mixed number 
was placed in parentheses with a minus in front of it. This was done to meet the requirement of the rule. And the rule required that the obtained answer should be preceded by minus.
The solution for this example can be written in a shorter form:
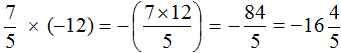
Example 8. Find the value of the expression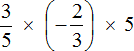 
An expression consists of several factors. According to the associative law of multiplication, if an expression consists of several factors, then the product will not depend on the order of operations. This allows us to calculate the expression in any order.
First, multiply 
and 
and multiply the resulting number with the remaining number 5. Let us omit the modules, so as not to overload the expression.
First act:
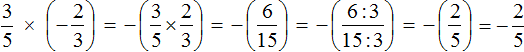
Second act:
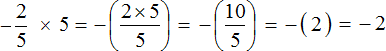
Answer: value of the expression 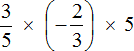is −2.
Example 9. Find the value of the expression: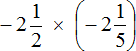 
Let's convert the mixed numbers into improper fraction:
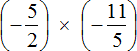
We obtained the multiplication of negative rational numbers. Multiply the modules of these numbers and put plus in front of the answer. You can skip the entry with modules, so as not to overload the expression
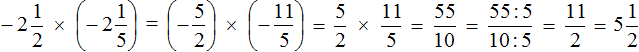
Example 10. Find the value of the expression
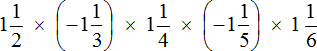
An expression consists of several factors. According to the associative law of multiplication, if an expression consists of several factors, then the product will not depend on the order of operations. This allows us to calculate the expression in any order.
Therefore let us calculate this expression from left to right in the order of the factors. Let us omit the entry with modules in order not to overload the expression
First act:
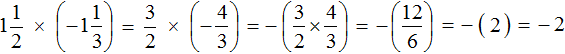
Second act:
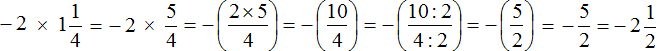
Third act:
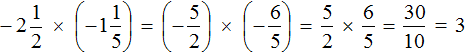
Fourth act:
Answer: value of expression 
Example 11. Find the value of the expression 
Recall the law of multiplication by zero. This law states that a product is zero if at least one of the factors is zero.
In our example, one of the factors is zero, so without wasting time we answer that the value of the expression is zero:
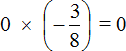
Example 12. Find the value of the expression 
A product is zero if at least one of the factors is zero.
In our example, one of the factors is zero, so without wasting time we answer that the value of expression is zero
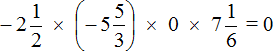
Example 13. Find the value of the expression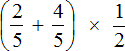 
You can use the order of operations and first calculate the expression in parentheses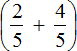 
and multiply the answer with fraction .
You can also use the distributive law of multiplication - multiply each summand of the sum 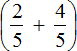by a fraction of and add the results. That's how we'll use it.
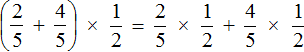
According to the order of operations, if an expression contains addition and multiplication, then multiplication should be performed first. Therefore, in the resulting new expression, we bracket the fractions that should be multiplied. This way we can clearly see which actions to perform first, and which later:
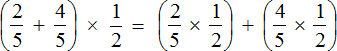
Next, we calculate the expression by actions. First, we calculate the expressions in parentheses and add the results
First act:
Second act:
Third act:
Answer: The value of expression 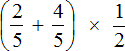is
The solution for this example can be written in a much shorter form. It would look as follows:
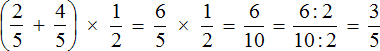
You can see that this example could be solved even in your mind. Therefore, you should develop the skill of analyzing the expression before you start solving it. It is likely that you can solve it in your head and save a lot of time and nerves. And on tests and exams, as you know, time is very expensive.
Example 14. Find the value of the expression -4.2 × 3.2
This is a multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer
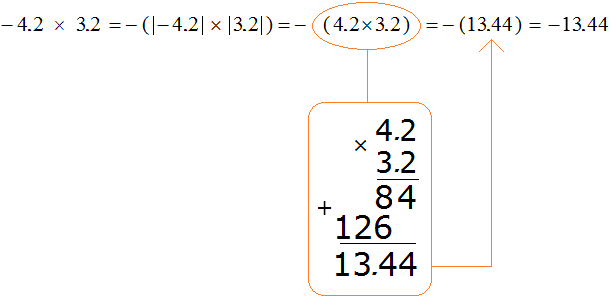
Notice how the modules of rational numbers were multiplied. In this case, in order to multiply modules of rational numbers, you had to be able to multiply decimals.
Example 15. Find the value of the expression -0.15 × 4
This is a multiplication of rational numbers with different signs. Multiply the modules of these numbers and put minus in front of the answer
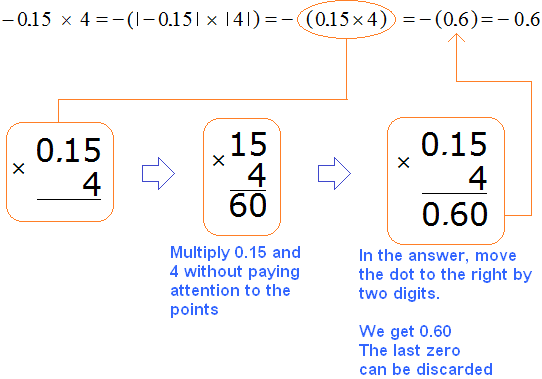
Notice how the modules of rational numbers were multiplied. In this case, to multiply modules of rational numbers, you had to be able to multiply a decimal and an integer.
Example 16. Find the value of the expression -4.2 × (-7.5)
This is a multiplication of negative rational numbers. Multiply the modules of these numbers and put plus in front of the answer
How to divide rational numbers
Division of rational numbers is reduced to the multiplication of the same numbers. To do this, the first fraction is multiplied by the inverse of the second fraction. Then the rules of multiplication of rational numbers are applied.
Example 1. Perform division: 
Multiply the first fraction by the inverse of the second fraction. The inverse of the second fraction is 
. Multiply the first fraction by it:
We got the multiplication of rational numbers with different signs. And we already know how to calculate such expressions. To do this we need to multiply the modules of the given rational numbers and put minus in front of the obtained answer.
Let's finish this example to the end. You can skip the entry with modules to avoid overloading the expression
Thus, the value of the expression is 
The detailed solution is as follows:
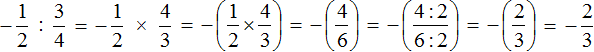
The short solution can be written as follows:
Example 2. Perform division 
Multiply the first fraction by the inverse of the second fraction. The inverse of the second fraction is 
. Multiply the first fraction by it:
The short solution can be written as follows:
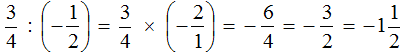
Example 3. Perform division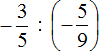 
Multiply the first fraction by the inverse of the second fraction. The inverse of the second fraction is 
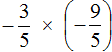
We obtained the multiplication of negative rational numbers. Let us perform this multiplication. You can skip the entry with modules in order not to overload the expression:
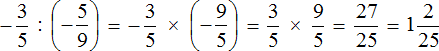
Example 4. Perform division 
In this case, multiply the first number -3 by the inverse of the fraction 
.
The inverse of the fraction is 
. Then apply the rule of multiplication of rational numbers with different signs:
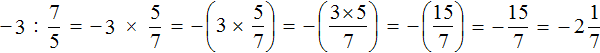
Example 6. Perform division 
Multiply the first fraction by the number inverse of 4.
The inverse of 4 is a fraction of . Multiply the first fraction 
by it.
Example 5. Perform division 
Multiply the first fraction by the number inverse of -3
The inverse of -3 is a fraction of 
Example 6: Find the value of the expression -14.4 : 1.8
This is the division of rational numbers with different signs. To calculate this expression, divide the modulus of the divisor by the modulus of the divisor and put minus sign in front of the answer
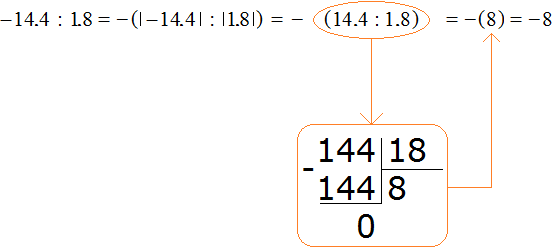
Notice how the modulus of the divisor was divided by the modulus of the divisor. In this case, we needed to be able to divide a decimal by another decimal.
If there is no desire to work with decimals (which is often the case), these decimals can be converted into mixed numbers, then you can convert these mixed numbers into improper fraction, and then deal directly with division.
Calculate the previous expression -14.4 : 1.8 this way. Convert the decimal fractions into mixed numbers:
Now convert these mixed numbers into improper fraction:
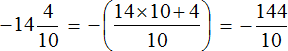
Now we can divide the fraction 
by the fraction 
. To do this, multiply the first fraction by the fraction inverse of the second fraction:
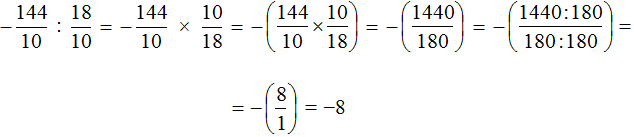
Example 7. Find the value of the expression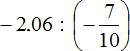 
Convert the decimal -2.06 to an improper fraction, and multiply that fraction by the inverse of the second fraction: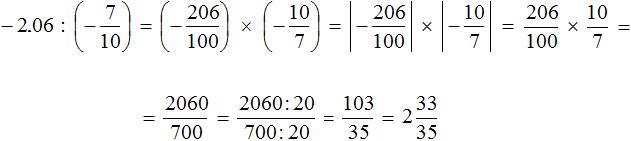
Example 8. Find the value of the expression -7.2 : (-0.6)
This is division of negative rational numbers. To do this division, multiply the first fraction by the inverse of the second fraction.
Move the comma in both fractions one digit to the right to obtain division
−72 : (−6)
Complex fraction
You will often find an expression in which the division of fractions is written with a fractional dash. For example, the expression can be written as follows:
What is the difference between expressions and ? Actually, there is no difference. The two expressions have the same meaning and can be equated:
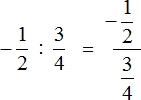
In the first case, the division sign is a colon and the expression is written on one line. In the second case, the division of fractions is written with a fractional dash. The result is a fraction, which is called a complex fraction.
When encountering such complex fractions, you must apply the same rules for dividing regular fractions. The first fraction must be multiplied by the inversed second fraction.
It is extremely inconvenient to use such fractions in the solution, so you can write them in an understandable form, using a colon instead of a fractional line as the division sign.
For example, let's write down the complex fraction in an understandable form. To do this, we first need to figure out where the first fraction is and where the second fraction is, because it is not always possible to do this correctly. Complex fractions can have several fractions that can be confusing. The main fractional line, which separates the first fraction from the second, is usually longer than the others.
After determining the main fractional line, you can easily figure out where the first fraction is and where the second fraction is:
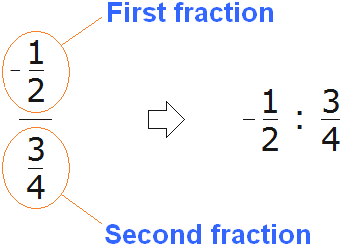
And then you can use the method of dividing fractions - multiply the first fraction by the inversed second one.
Example 2. Let's write down the complex fraction 
in understandable form
Find the main fractional line (it is the longest) and see that the integer -3 is divided by an ordinary fraction .
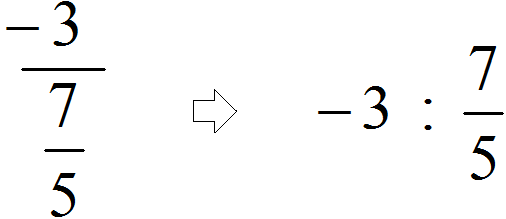
And if we mistakenly took the second fractional line as the main line (the shorter one), then it would turn out that we divide the fraction 
by the integer 5
In this case, even if this expression is calculated correctly, the problem will not be solved correctly, because the divisor in this case is the number -3, and the divisor is the fraction .
Example 3. Let us write down the multi-story fraction 
in understandable form
Find the main fractional line (it is the longest) and see that the fraction 
is divided by the integer 2
And if we mistakenly took the first fractional line as the main line (the shorter one), it would turn out that we are dividing an integer -5 by a fraction 
In this case, even if this expression is calculated correctly, the problem will not be solved correctly, because the divisor in this case is a fraction , and the divisor is an integer 2.
Despite the fact that complex fractions are awkward to work with, we will encounter them very often, especially when studying higher mathematics.
Naturally, it takes extra time and space to convert complex fractions into an understandable form. So we can use a faster method. This method is convenient and yields a ready-made expression with the first fraction multiplied by the inversed second one.
This method is implemented as follows:
If the fraction is four stories, such as , then the number on the first floor is raised to the top floor. And the digit on the second floor goes up to the third floor. The obtained digits should be connected by multiplication signs ( × )
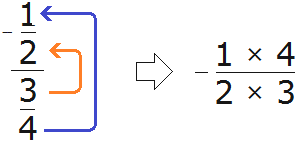
As a result, bypassing the intermediate notation , we get a new expression 
, in which the first fraction is already multiplied by the fraction inverse of the second. This is very convenient!
To avoid mistakes when using this method, you can follow the following rule:
From the first to the fourth. From the second to the third.
The rule refers to the "levels". The figure from the first "level" should be raised to the fourth "level". And the figure from the second "level" should be raised to the third "level".
Let's try to calculate the complex fraction 
using the above rule.
So, the number on the first "level" goes up to the fourth"level", and the number on the second "level" goes up to the third "level"
As a result, bypassing the intermediate notation 
we get a new expression 
, in which the first fraction is already multiplied by the fraction inverse of the second. Then we can use the available knowledge:
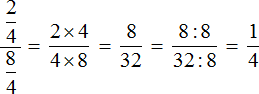
Example 4. Let's try to calculate the complex fraction using the new scheme.
There is only the first, second and fourth "level". The third "level" is missing. But we do not deviate from the basic scheme: we raise the figure from the first "level" to the fourth "level". And since the third "level" is missing, we leave the figure on the second "level" as it is
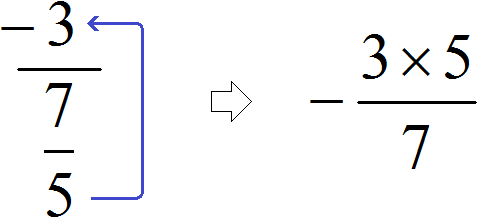
As a result, bypassing the intermediate notation we have a new expression 
, in which the first number -3 is already multiplied by the fraction inverse of the second. Next, we can use the existing knowledge:
Example 5. Let's try to calculate the complex fraction using the new scheme.
There is only the second, third and fourth "level". The first "level" is missing. Since the first "level" is missing, we don't need to go up to the fourth "level", but we can raise the number from the second "level" to the third:
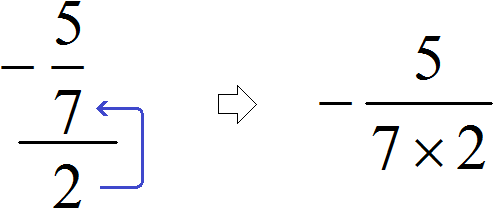
As a result, bypassing the intermediate notation 
, we have a new expression 
, in which the first fraction is already multiplied by the number inverse of the divisor. Next, we can use the existing knowledge:
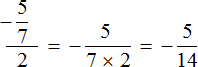
Using variables
If an expression is complicated and you think it will confuse you as you solve a problem, you can put part of it into a variable, and then work with that variable.
Mathematicians often do this. They break a complex problem into easier subproblems and solve them. Then they assemble the solved subtasks into a single whole. This is a creative process, and it takes years of hard practice to learn.
The use of variables is justified when working with complex fractions. For example:
Find the value of the expression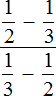 
So there is a fractional expression in the numerator and a fractional expression in the denominator. In other words, we are again faced with the complex fraction that we dislike so much.
The expression in the numerator 
can be written into a variable with any name, for example:
But in mathematics, in such a case, it is customary to name variables with large Latin letters. Let us not break this tradition, and denote the first expression by the capital Latin letter - A
And the expression in denominator 
can be denoted by the capital Latin letter - B
Now our original expression 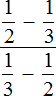takes the form 
. That is, we have replaced the numeric expression with a letter expression, having previously entered the numerator and denominator in the variables A and B.
Now we can separately calculate the values of variable A and the value of variable B. We insert the finished values into the expression .
Let us find the value of variable A
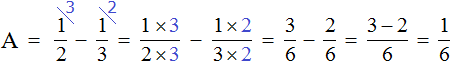
Let's find the value of variable B
Now substitute their values into the main expression instead of variables A and B:
We got a complex fraction in which we can use the scheme "from the first to the fourth, from the second to the third", that is, the figure that is on the first "level" to raise to the fourth "level", and the figure that is on the second "level" to raise to the third "level". Further calculation is not too difficult:
Thus, the value of the expression 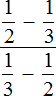is -1.
Of course, we looked at the simplest example, but our goal was to see how we could use variables to make things easier for ourselves, so that we could minimize errors.
Note also that the solution to this example can be written without using variables. It would look like this
This solution is faster and shorter, and in this case it would be better to write it that way, but if an expression turns out to be complex, consisting of several parameters, parentheses, roots, and powers, it is advisable to calculate it in several steps, putting some of its expressions into variables.
Exercises
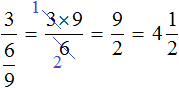
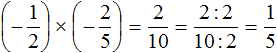
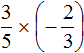
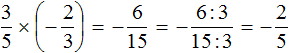
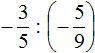
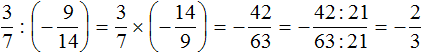
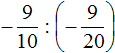
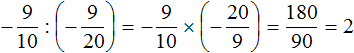
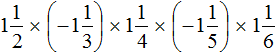
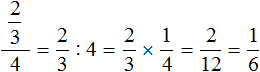
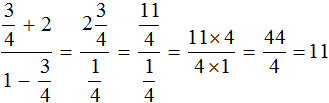
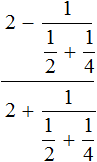
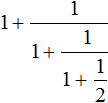
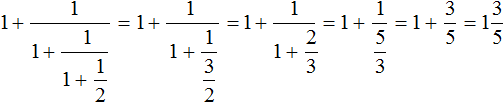
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.