We continue to learn the basics of algebra. In this lesson we will learn how to expand algebraic expressions. To expand parentheses means to get rid of the parentheses in an expression.
To expand parentheses, you have to learn two rules by heart. With regular practice, you will be able to expand parentheses easily, and the rules that you had to memorize can be safely forgotten.
The first rule of Expanding parentheses
Consider the following expression:
8 + (−9 + 3)
The value of this expression is 2. Expand the parentheses in this expression. To expand parentheses means to get rid of them without affecting the value of the expression. That is, the value of the expression 8 + (-9 + 3) must still be 2.
The first rule of expanding parentheses is as follows:
When you expand parentheses, if there is a plus sign in front of the parentheses, that plus is removed with the parentheses.
So, we see that in the expression 8 + (-9 + 3) there is a plus before the parentheses. This plus must be removed together with the parentheses. In other words, the parentheses disappear along with the plus sign in front of them. And what was in parentheses will be written unchanged:

We obtained an expression without parentheses 8-9+3. This expression equals 2, just as the previous expression with parentheses was equal to 2.
8 + (−9 + 3) = 2
8 − 9 + 3 = 2
Thus, between the expressions 8+(-9+3) and 8-9+3 we can put an equal sign, because they are equal to the same value:
8 + (−9 + 3) = 8 − 9 + 3
2 = 2
Example 2. Expand parentheses in the expression 3 + (-1 - 4)
There is a plus before the parentheses, so the plus is dropped together with the parentheses. What was in parentheses will remain unchanged:
3 + (−1 − 4) = 3 − 1 − 4
Example 3. Expand parentheses in the expression 2 + (-1)
There is a plus before the parentheses, so the plus is dropped together with the parentheses. What was in parentheses will remain unchanged:
2 + (−1) = 2 − 1
In this example, expanding parentheses has become a kind of inverse operation replacing subtraction with addition. What does this mean?
In the expression 2 - 1 there is subtraction, but it can be replaced by addition. Then we get 2 + (-1). But if you expand the parentheses in the expression 2 + (-1), you get the original 2 - 1.
So you can use the first bracketing rule to simplify expressions after some transformations. That is, get rid of parentheses and make it simpler.
For example, simplify the expression 2a + a- 5b + b.
To simplify this expression, you can combine like terms. Recall that in order to combine the like terms, add the coefficients of the like terms and multiply the result by the common letter part:
![]()
We obtain the expression 3a + (-4b). In this expression we expand the parentheses. There is a plus before the parentheses, so we use the first rule of expanding parentheses, i.e. we drop the parentheses together with the plus in front of the parentheses:
3a + (−4b) = 3a − 4b
Thus, the expression 2a+a-5b+b is simplified to 3a-4b.
After expanding one of the parentheses, there may be other parentheses along the way. Apply the same rules to them as to the first. For example, expand parentheses in the following expression:
2 + (−3 + 1) + 3 + (−6)
Here are two places where parentheses need to be expanded. In this case, the first rule of expanding parentheses applies, namely, dropping the parentheses along with the plus sign in front of the parentheses:
2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Example 3. Expand the parentheses in the expression 6+(-3)+(-2)
In both places where there are parentheses, there is a plus in front of them. Here again the first rule of parentheses expansion applies:
6 + (−3) + (−2) = 6 − 3 − 2
Sometimes the first summand in parentheses is written without a sign. For example, in the expression 1+(2+3-4) the first summand in parentheses 2 is written without a sign. The question arises: what sign will be in front of the two after the parentheses and the plus sign in front of the parentheses are dropped? The answer is obvious: there will be a plus sign before the two.
In fact, even being in parentheses there is a plus in front of the two, but we don't see it due to the fact that it is not written down. We have already said that the full record of positive numbers looks like +1, +2, +3. But pluses are traditionally not written down, so we see the usual positive numbers 1, 2, 3.
Therefore, to expand the parentheses in the expression 1+(2+3-4), you need to remove the parentheses as usual, along with the plus sign in front of the parentheses, but write the first summand that was in the parentheses with the plus sign:
1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Example 4. Expand parentheses in the expression -5 + (2 - 3)
There is a plus sign before the parentheses, so we apply the first rule of expanding the parentheses, namely, we drop the parentheses together with the plus sign before the parentheses. But the first summand in parentheses should be written with a plus sign:
−5 + (2 − 3) = −5 + 2 − 3
Example 5. Expand parentheses in the expression (-5)
There is a plus sign before the parentheses, but it is not written because there are no other numbers or expressions before it. Our task is to remove the parentheses by applying the first rule of explaining parentheses, namely, to remove the parentheses together with the plus (even if it is invisible)
(−5) = −5
Example 6. Expand parentheses in the expression 2a + (-6a + b)
There is a plus sign before the parentheses, so the plus is dropped together with the parentheses. What was in parentheses will be written unchanged:
2a + (−6a + b) = 2a −6a + b
Example 7. Expand parentheses in the expression 5a + (-7b + 6c) + 3a + (-2d)
There are two places in this expression where parentheses need to be expanded. In both places there is a plus in front of the parentheses, so that plus is dropped along with the parentheses. What was in parentheses will be written unchanged:
5a + (−7b + 6c) + 3a + (−2d) = 5a −7b + 6c + 3a − 2d
The second rule of Expanding parentheses
Now consider the second rule of expanding parentheses. It applies when parentheses are preceded by a minus sign .
If there is a minus before the parentheses, that minus is removed along with the parentheses, but the summands ,that were in the parentheses, change their sign to the opposite one.
For example, expand parentheses in the following expression
5 − (−2 − 3)
We see that there is a minus in front of the parentheses. So we need to apply the second rule of expansion, namely remove the parentheses together with the minus in front of these parentheses. In this case, the summands that were in parentheses will change their sign to the opposite one:

We obtained an expression without parentheses 5 + 2 + 3. This expression is equal to 10, just as the previous expression with parentheses was equal to 10.
5 − (−2 − 3) = 10
5 + 2 + 3 = 10
Thus, between the expressions 5-(-2-3) and 5+2+3 we can put an equal sign, because they are equal to the same value:
5 − (−2 − 3) = 5 + 2 + 3
10 = 10
Example 2. Expand parentheses in the expression 6 - (-2 - 5)
We use the second rule of explaining parentheses: we drop the parentheses together with the minus sign before the parentheses. In this case, write the summands that were in parentheses with opposite signs:
6 − (−2 − 5) = 6 + 2 + 5
Example 3. Expand parentheses in the expression 2 - (7 + 3)
There is a minus sign before the parentheses, so we apply the second rule of expanding parentheses:
2 − (7 + 3) = 2 − 7 − 3
Example 4. Expand parentheses in the expression -(-3 + 4)
There is a minus sign before the parentheses, so we apply the second rule of expanding parentheses:
−(−3 + 4) = 3 − 4
Example 5. Expand parentheses in the expression -(-8 - 2) + 16 + (-9 - 2)
There are two places where you need to expand parentheses. In the first case we need to apply the second rule, and when it comes to the expression +(-9 - 2) we need to apply the first rule:
−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2
Example 6. Expand parentheses in the expression -(-a - 1)
There is a minus sign before the parentheses, so we apply the second rule of expanding parentheses:
−(−a − 1) = a + 1
Example 7. Expand parentheses in the expression −(4a + 3)
There is a minus sign before the parentheses, so we apply the second rule of expanding parentheses:
−(4a + 3) = −4a − 3
Example 8. Expand parentheses in the expression a − (4b + 3) + 15
There is a minus before the parentheses, so we apply the second rule of expanding parentheses:
a − (4b + 3) + 15 = a − 4b − 3 + 15
Example 9. Expand parentheses in the expression 2a + (3b − b) − (3c + 5)
There are two places where you need to expand parentheses. In the first case you need to apply the first rule, and when it comes to the expression -(3c+5) you need to apply the second rule:
2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5
Example 10. Expand parentheses in the expression −a − (−4a) + (−6b) − (−8c + 15)
There are three places where you need to expand parentheses. First you apply the second of expanding parentheses, then the first, and then the second again:
−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15
What you need to know about expanding parentheses
The parentheses rules we have just discussed are based on the distributive law of multiplication:
a(b+c) = ab + ac
In fact, expanding parentheses is the procedure by which a common factor is multiplied by each summand in the parentheses. As a result of such multiplication the parentheses are removed.
For example, expand the parentheses in the expression 3×(4+5)
3 × (4 + 5) = 3 × 4 + 3 × 5
Therefore, if you want to multiply a number by an expression in parentheses (or an expression in parentheses multiplied by a number), you must say expand the parentheses.
But how does the distributive law of multiplication relate to the expanding parentheses rules we discussed earlier?
The point is that any parentheses are preceded by a common factor. In the example 3×(4+5), the common factor is 3. And in the example a(b+c) the common factor is the variable a.
If there are no numbers or variables before the parentheses, then the common factor is 1 or -1, depending on which sign is before the parentheses. If there is a plus sign before the parentheses, then the common factor is 1. If there is a minus before the parentheses, then the common factor is -1.
For example, expand the parentheses in the expression -(3b-1). There is a minus before the parentheses, so we must use the second rule of expanding parentheses, i.e. remove the parentheses together with the minus before the parentheses. Write the expression that was in parentheses with opposite signs:
−(3b − 1) = −3b + 1
We have expanded parentheses using the bracket expanding rule. But the same parentheses can be expanded using the distributive law of multiplication. To do this, first write down before the parentheses the common factor 1, which was not written down:
−1(3b −1)
The minus that used to be in front of the parentheses refers to that unit. Now you can expand the parentheses by applying the distributive law of multiplication. To do this, multiply the common factor -1 by each summand in parentheses and add the results.
For convenience, replace the difference in parentheses with the sum:
−1(3b −1) = −1( 3b + (−1) )
Then multiply the total factor -1 by each summand in parentheses:
−1(3b −1) = −1(3b + (−1)) = −1 × 3b + (−1) × (−1) = −3b + 1
Like last time, we got the expression -3b+1. Everyone will agree that this time it takes more time to solve such a simple example. Therefore, it is more reasonable to use the ready-made rules for expanding parentheses, which we discussed in this lesson:
−(3b − 1) = −3b + 1
But it's good to know how these rules work.
In this lesson we learned another identity transformation. Together with the expanding parentheses, factorising by taking out common factors, and the like terms, we can slightly expand the range of problems to be solved. For example:
Expand parentheses and combine like terms in the following expression:
![]()
Here we need to perform two actions - first, expand the parentheses, and then combine like terms. So, in order:
1) Expand the parentheses:
![]()
2) Combine like terms:
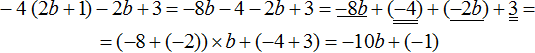
In the resulting expression -10b+(-1) you can expand the parentheses:

Example 2. Expand parentheses and combine like terms in the following expression:
![]()
1) Expand the parentheses:
![]()
2) Combine like terms: This time, to save time and space, we will not write down how the coefficients are multiplied by the total letter part
![]()
Example 3. Simplify the expression 8m+3m and find its value at m = -4
1) First, simplify the expression. To simplify the expression 8m+3m, we can take the common factor m out of parentheses:
8m+3m = m(8+3)
2) Find the value of the expression m(8+3) when m = -4. To do this, substitute m(8+3) for -4
m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44
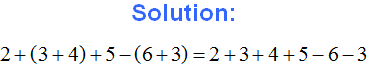
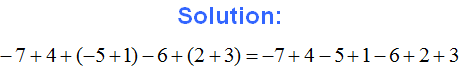
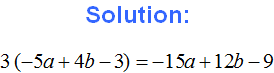
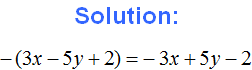
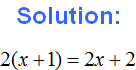
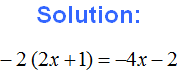
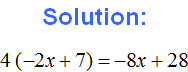
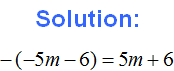
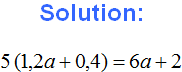
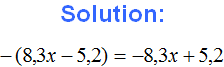
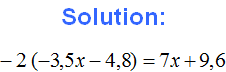
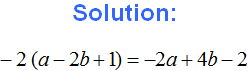
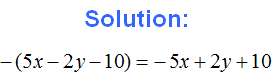
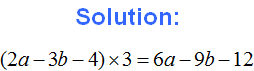
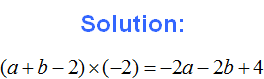
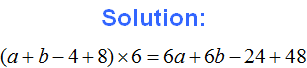
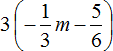
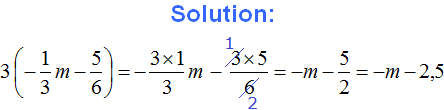
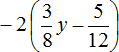
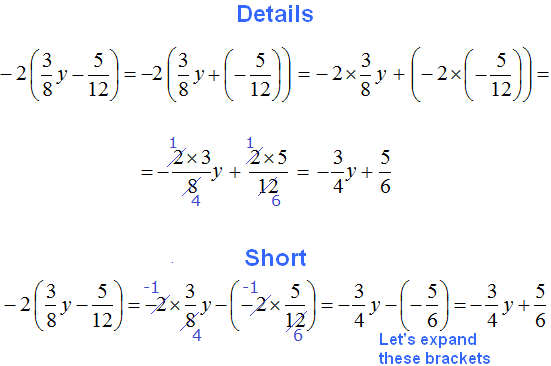
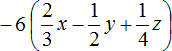
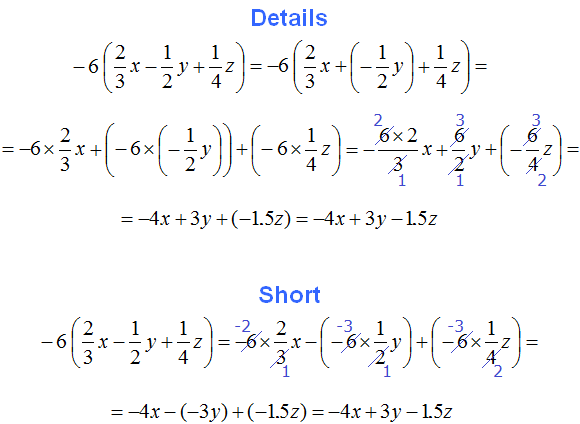
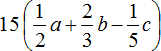
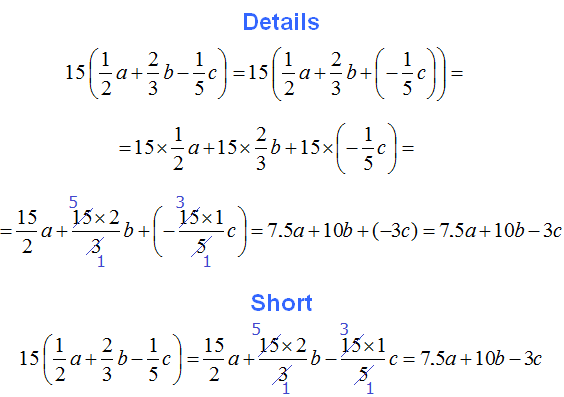
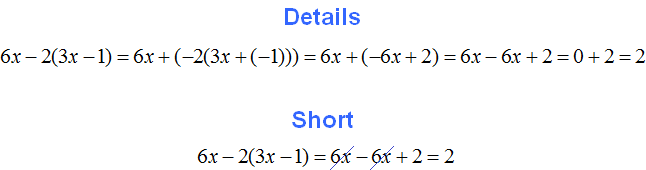
Comments