We continue to study polynomials. In this lesson we will learn how to divide them.
Division of a polynomial by a monomial
To divide a polynomial by a monomial, divide each term of the polynomial by that monomial, then add the resulting quotients.
For example, divide the polynomial 15x2y3 + 10xy2 + 5xy3 by the monomial xy. Write this division as a fraction:
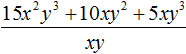
Now divide each term of the polynomial 15x2y3 + 10xy2 + 5xy3 by the monomial xy. The resulting quotients will be added together:
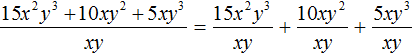
We obtained the usual division of monomials. Let's perform this division:
Thus, dividing the polynomial 15x2y3 + 10xy2 + 5xy3 by the monomial xy results in the polynomial 15xy2 + 10y + 5y2.
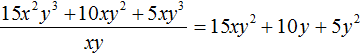
When dividing one number by another, the quotient must be such that when it is multiplied by the divisor, the result is the dividend. This rule also holds when dividing a polynomial by a monomial.
In our example, the product of the resulting polynomial 15xy2 + 10y + 5y2 and the divisor xy should be equal to the polynomial 15x2y3 + 10xy2 + 5xy3, i.e. the original dividend. Let's check if this is true:
(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3
Dividing a polynomial by a monomial is very similar to adding fractions with common denominators. We remember that to add fractions with identical denominators, you add their numerators and leave the denominator unchanged.
For example, to add fractions 
, 
, and 
, write the following expression:
If we calculate the expression 
, we get a fraction 
, the value of which is 1.5.
In this case, we can return expression to the initial state 
, and calculate each fraction separately, then add up the resulting quotients. The result will still be 1.5
The same thing happens when you divide a polynomial by a monomial. A monomial is the common denominator of all the terms of a polynomial. For example, dividing a polynomial ax + bx + cx by a polynomial x results in three fractions with a common denominator x
Calculating each fraction will result in a polynomial a + b + c
Example 2. Divide polynomial 8m3n + 24m2n2 by monomial 8m2n
Example 3. Divide polynomial 4c2d − 12c4d3 by monomial −4c2d
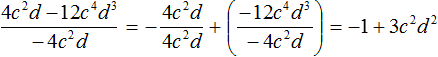
Division of a monomial by a polynomial
There is no identity transformation to divide a monomial by a polynomial.
Suppose we want to divide a monomial 2xy by a polynomial 5x + 3y + 5.
The result of this division should be a polynomial whose multiplication with the polynomial 5x + 3y + 5 gives a monomial 2xy. But there is no polynomial whose multiplication with the polynomial 5x + 3y + 5 would result in a monomial 2xy, since the multiplication of polynomials results in a polynomial, not a monomial.
But in the books you can find tasks to find the value of an expression with given values of the variables. In the initial expressions of such tasks, there may be a division of a monomial by a polynomial. In this case, no transformations need to be performed. It is enough to substitute the values of the variables in the original expression and calculate the resulting numerical expression.
For example, find the value of expression 
when x = 2.
Expression is a division of a monomial by a polynomial. In this case we will not be able to perform any transformations. The only thing we can do is substitute number 2 in the original expression instead of the x variable and find the value of the expression:
Division of a polynomial by a polynomial
If you multiply the first polynomial by the second polynomial, you get a third polynomial. For example, if you multiply polynomial x + 5 by polynomial x + 3, you get polynomial x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
(x + 5)(x + 3) = x2 + 8x + 15
If you divide the product by the multiplier, you get the multiplicand. This rule applies not only to numbers, but also to polynomials.
Then according to this rule, dividing the polynomial x2 + 8x + 15 by the polynomial x + 3 should result in the polynomial x + 5.
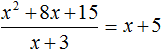
Dividing a polynomial by a polynomial is done by of long division. The difference will be that when dividing a polynomial, you don't need to determine the first incomplete divisor, as in the case of dividing regular numbers.
Perform the long division of the polynomial x2 + 8x + 15 by the polynomial x + 3. In this way we will see step by step how the polynomial x + 5 is obtained.
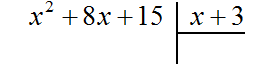
In this case we know the result beforehand. It will be the polynomial x + 5. But more often than not, the result is unknown. So we will comment on the solution as if the result were unknown.
The result of division should be a new polynomial. Members of this polynomial will appear one by one in the process of division.
Now our task is to find the first term of the new polynomial. How do we do this?
When we initially multiplied the polynomials x + 5 and x + 3, we first multiplied the first term of the first polynomial by the first term of the second polynomial. In this way we got the first term of the third polynomial:
If we divide the first term of the third polynomial by the first term of the second polynomial, we get the first term of the first polynomial. This is what we need. After all, we have to arrive at the polynomial x + 5.
The same principle of finding the first term will be followed when solving other tasks on dividing polynomials.
So, to find the first term of a new polynomial, divide the first term of the dividend by the first term of the divisor.
If the first term of the dividend (in our case it is x2) is divided by the first term of the divisor (which is x), we get x. That is, the first term of the new polynomial is x. Write it down at the right angle:
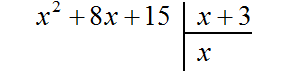
Now, as with dividing regular numbers, multiply x by the divisor x + 3. At this point, you should be able to multiply a monomial by a polynomial. When x is multiplied by x + 3, you get x2 + 3x. Write this polynomial under the divisor x2 + 8x + 15 so that the like terms are under each other:
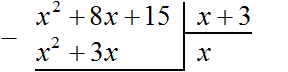
Now subtract x2 + 8x + 15 from the dividend x2 + 3x. Subtract like terms from like terms. If you subtract x2 from x2, you get 0. Zero is not written down. Next, if you subtract 3x from 8x, you get 5x. Write 5x so that the term is below the terms 3x and 8x
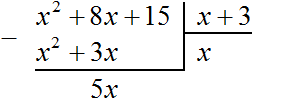
Now, as with dividing regular numbers, we take down the next term of the divisor. The next term is 15. It should be written down together with its sign:
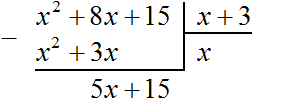
Now divide the polynomial 5x + 15 by x + 3. To do this we need to find the second term of the new polynomial. To find it, divide the first term of the dividend (now it is the term 5x) by the first term of the divisor (that is the term x). If you divide 5x by x, you get 5. So the second term of the new polynomial is 5. Write it under the right angle, together with its sign (term 5 is positive in this case)
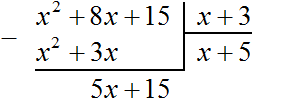
Now multiply 5 by the divisor x + 3. When you multiply 5 by x + 3, you get 5x + 15. Write this polynomial under the dividend 5x + 15
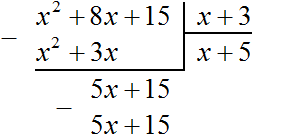
Now subtract 5x + 15 from the dividend 5x + 15. If you subtract 5x + 15 from 5x + 15 you get 0.
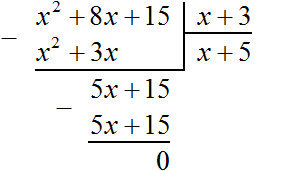
This completes division.
After division, you can check by multiplying the quotient by the divisor. In this case, if the quotient of x + 5 is multiplied by the divisor of x + 3, you should get the polynomial x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
Example 2. Divide the polynomial x2 - 8x + 7 by the polynomial x - 7
Write long division:
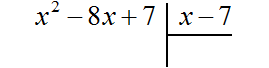
Find the first term of the quotient. Divide the first term of the dividend by the first term of the divisor, we get x. Write x at the right corner:
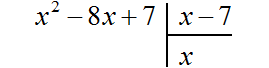
Multiply x by x - 7 to get x2 - 7x. Write this polynomial under the dividend x2 - 8x + 7, so that the like terms are located under each other:
Subtract x2 - 8x + 7 from the polynomial x2 - 7x. Subtracting x2 from x2 yields 0. Zero is not written down. And subtracting -7x from -8x gives -x, because -8x - (-7x) = -8x + 7x = -x. Write -x under the terms -7x and -8x. Then write down the next term 7
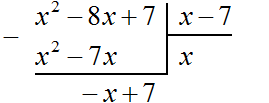
Be careful when subtracting negative terms. Often mistakes are made at this stage. If columnar subtraction is difficult at first, you can use the regular columnar subtraction of polynomials that we studied earlier. To do this, you need to write out the dividend and subtract from it the polynomial below it. The advantage of this method is that the next terms of the dividend don't need to be subtracted - they will automatically go into the new dividend. Let's use this method:
Let's return to our task. Let's divide the polynomial -x + 7 by x - 7. To do this we need to find the second term of the quotient. To find it, divide the first term of the dividend (now it is the term -x) by the first term of the divisor (that is the term x). If -x is divided by x, you get -1. Write -1 under the right-hand corner along with its sign:
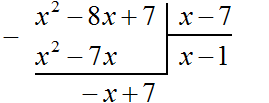
Multiply -1 by x - 7 to get -x + 7. Write this polynomial under the dividend -x + 7
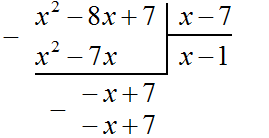
Now subtract -x + 7 from -x + 7. If you subtract -x + 7 from -x + 7 you get 0
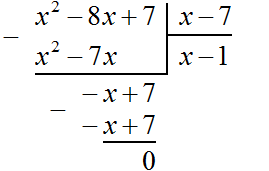
The division is complete. Thus, the quotient of the division of the polynomial x2 - 8x + 7 by the polynomial x - 7 is x - 1
Let's check. Multiply the quotient x - 1 by the divisor x - 7. We should have a polynomial x2 - 8x + 7
(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7
Example 3. Divide the polynomial x6 + 2x4 + x7 + 2x5 by the polynomial x2 + x3
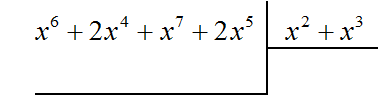
Find the first term of the quotient. Divide the first term of the dividend by the first term of the divisor, we get x4
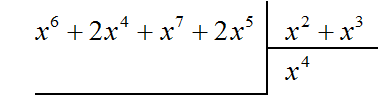
Multiply x4 by the divisor x2 + x3 and write the result under the dividend. If x4 is multiplied by x2 + x3 you get x6 + x7. Write the terms of this polynomial under the dividend, so that like terms are located under each other:
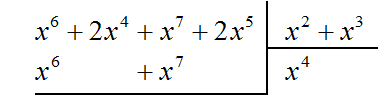
Now subtract the polynomial x6 + x7 from the dividend. Subtracting x6 from x6 will result in 0. Subtracting x7 from x7 will also result in 0. The remaining terms 2x4 and 2x5 will be written off:
A new dividend 2x4 + 2x5 is obtained. The same dividend could be obtained by writing out separately the polynomial x6 + 2x4 + x7 + 2x5 and subtracting from it the polynomial x6 + x7
Divide the polynomial 2x4 + 2x5 by the divisor x2 + x3. As before, first divide the first term of the dividend by the first term of the divisor, we get 2x2. Write this term in the quotient:
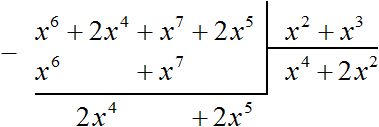
Multiply 2x2 by the divisor x2 + x3 and write the result under the dividend. If 2x2 is multiplied by x2 + x3 you get 2x4 + 2x5. Write the terms of this polynomial under the dividend, so that like terms are located under each other. Then do the subtraction:
Subtracting polynomial 2x4 + 2x5 from polynomial 2x4 + 2x5 resulted in 0, so the division was successful.
In the intermediate calculations the terms of the new dividend were located away from each other, forming large distances. This was because when multiplying the quotient by the divisor, the results were written so that like terms were located under each other.
These distances between terms of a new dividend are formed when the terms of the original polynomials are arranged disorderly. Therefore before division, it is desirable to order the terms of the original polynomials in descending order of powers. Then the solution will have a neater and clearer form.
Solve the previous example by arranging the terms of the original polynomials in descending order of powers. If we order the terms of the polynomial x6 + 2x4 + x7 + 2x5 in descending order of powers, we get the polynomial x7 + x6 + 2x5 + 2x4. And if we order the terms of the polynomial x2 + x3 in descending order of powers, we get the polynomial x3 + x2
Then the division of the polynomial x6 + 2x4 + x7 + 2x5 by the polynomial x2 + x3 will take the following form:
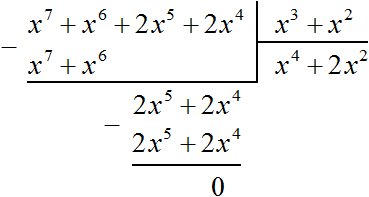
The division is complete. Thus, the quotient of the division of the polynomial x6 + 2x4 + x7 + 2x5 by the polynomial x2 + x3 is x4 + 2x2
Let's check. Multiply the quotient x4 + 2x2 by the divisor x2 + x3. We should have a polynomial x6 + 2x4 + x7 + 2x5
(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
When multiplying polynomials, the terms of the original polynomials should also be ordered in descending order of powers. Then the terms of the resulting polynomial will also be ordered in descending order of powers.
Rewrite the multiplication of (x4 + 2x2)(x2 + x3) by ordering the terms of the polynomials in descending order of powers.
(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4
Example 4. Divide the polynomial 17x2 − 6x4 + 5x3 − 23x + 7 by the polynomial 7 − 3x2 − 2x
Arrange the terms of the original polynomials in descending order of powers and perform this division:
So,
Example 5. Divide polynomial 4a4 − 14a3b − 24a2b2 − 54b4 by polynomial a2 − 3ab − 9b2
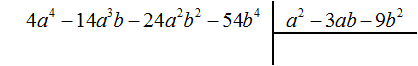
Find the first term of the quotient. Divide the first term of the dividend by the first term of the divisor, we get 4a2. Write 4a2 in the quotient:
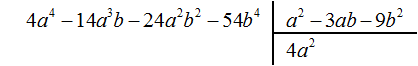
Multiply 4a2 by the divisor a2 - 3ab - 9b2 and write the result under the dividend:
Subtract the resulting polynomial 4a4 − 12a3b − 36a2b2 from the dividend.
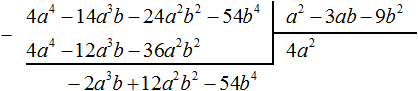
Now divide −2a3b + 12a2b2 − 54b4 by the divisor a2 − 3ab − 9b2. Divide the first term of the dividend by the first term of the divisor, we get -2ab. Write -2ab in the quotient:
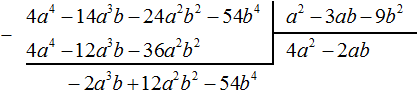
Multiply -2ab by the divisor a2 − 3ab − 9b2 and write the result under the dividend −2a3b + 12a2b2 − 54b4
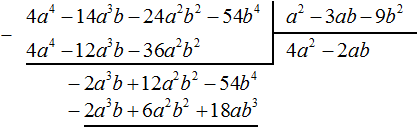
Subtract −2a3b + 12a2b2 − 54b4 from the polynomial −2a3b + 12a2b2 − 18ab3. When subtracting like terms, we find that -54b4 and 18ab3 are not like terms, so their subtraction will not give any transformation. In this case we deduct where it is possible, namely, we subtract −2a3b from −2a3b and 6a2b2 from 12a2b2, and write down the subtraction of 18ab3 from -54b4 as the difference −54b4 − (+18ab3) or −54b4 − 18ab3
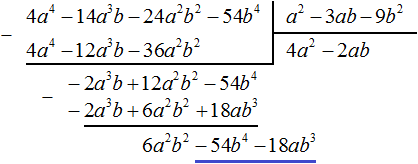
The same result can be obtained if you perform the subtraction of polynomials to a string using brackets:
Let's return to our task. Divide 6a2b2 − 54b4 − 18ab3 by the divisor a2 − 3ab − 9b2. Divide the first term of the dividend by the first term of the divisor, we get 6b2. Write 6b2 in the quotient:
Multiply 6b2 by the divisor a2 − 3ab − 9b2 and write the result under the dividend 6a2b2 − 54b4 − 18ab3. Immediately subtract this result from the dividend 6a2b2 − 54b4 − 18ab3
The division is complete. Thus, the quotient of the division of the polynomial 4a4 − 14a3b − 24a2b2 − 54b4 by the polynomial a2 − 3ab − 9b2 is 4a2 − 2ab + 6b2.
Let's check. Multiply the quotient 4a2 − 2ab + 6b2 by the divisor a2 − 3ab − 9b2. We should have a polynomial 4a4 − 14a3b − 24a2b2 − 54b4
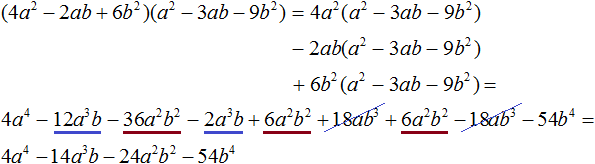
Division of a polynomial by a polynomial with remainder
As with dividing regular numbers, dividing a polynomial by a polynomial can produce a remainder.
First, let's recall the division of regular numbers with a remainder. For example, let's divide 15 by 2. With a remainder this division will be done as follows:
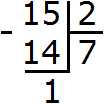
That is, when you divide 15 by 2 you get 7 integers and 1 in the remainder. The answer is written as follows:
A rational number 
is read as seven whole numbers plus one second. The plus sign is traditionally not written down. But if dividing a polynomial by a polynomial produces a remainder, then this plus must be written.
For example, if you divide a polynomial a by a polynomial b to get a quotient c and leave a remainder q, then the answer will be written as follows:
For example, divide the polynomial 2x3 − x2 − 5x + 4 by the polynomial x - 3
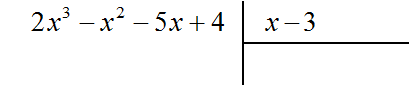
Find the first term of the quotient. Divide the first term of the dividend by the first term of the divisor, we get 2x2. Write 2x2 in the quotient:
Multiply 2x2 by the divisor x - 3 and write the result under the dividend:
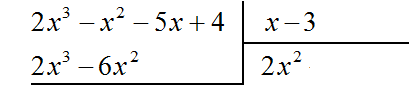
Subtract the resulting polynomial 2x3 − 6x2 from the dividend.
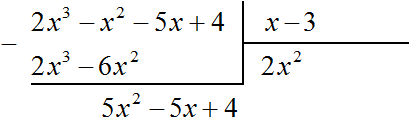
Now divide 5x2 - 5x + 4 by the divisor x - 3. Divide the first term of the dividend by the first term of the divisor, we get 5x. Write 5x in the quotient:
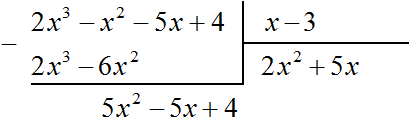
Multiply 5x by the divisor x - 3 and write the result under the dividend 5x2 − 5x + 4
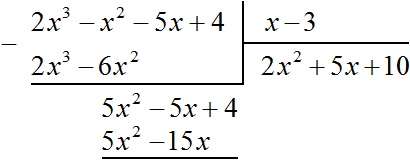
Subtract from the polynomial 5x2 − 5x + 4 the polynomial 5x2 - 15x
Now divide 10x + 4 by the divisor x - 3. Divide the first term of the dividend by the first term of the divisor, we get 10. Write 10 in the quotient:
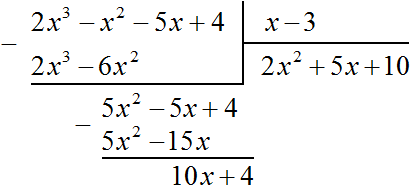
Multiply 10 by the divisor x - 3 and write the result under the dividend 10x + 4. Immediately subtract this result from the dividend 10x + 4
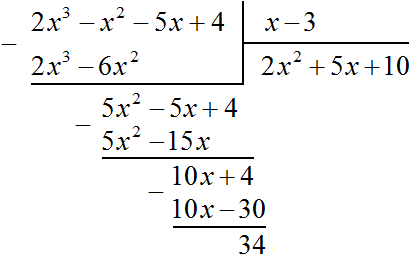
The number 34 resulting from subtracting the polynomial 10x - 30 from the polynomial 10x + 4 is the remainder. We cannot find the next term of the quotient which, when multiplied with a divisor of x - 3, would give us 34 as a result.
Therefore, dividing the polynomial 2x3 − 2x2 − 5x + 4 by the polynomial x - 3 yields 2x2 + 5x + 10 and 34 in the remainder. The answer is written in the same way as when dividing regular numbers. First write down the integer part (it is located under the right corner) plus the remainder divided by the divisor:
When division of polynomials is impossible
Dividing a polynomial by a polynomial is impossible if the power of the dividend is less than the power of the divisor.
For example, you cannot divide a polynomial x3 + x by a polynomial x4 + x2 because the dividend is a third power polynomial and the divisor is a fourth power polynomial.
Contrary to this prohibition, you can try to divide the polynomial x3 + x by the polynomial x4 + x2, and even get the quotient x−1, which when multiplied with the divisor will give the dividend:
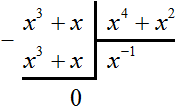
But dividing a polynomial by a polynomial should result in a polynomial, and the quotient x−1 is not a polynomial. After all, a polynomial consists of a monomial, and a monomial is the product of numbers, variables, and powers. The expression x−1 is a fraction 
,which is not a product.
Suppose there is a rectangle with sides 4 and 2
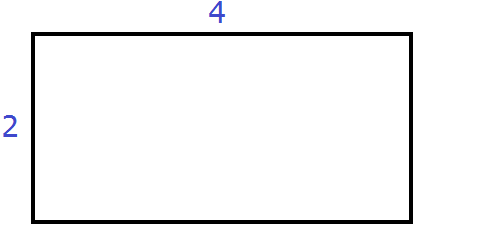
The area of this rectangle will be 4 × 2 = 8 square units.
Let's increase the length and width of this rectangle by x
Let's complete the missing sides:
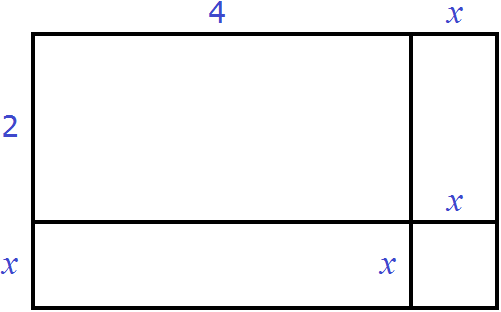
Now the rectangle has length x + 4 and width x + 2. The area of this rectangle is equal to the product (x + 4)(x + 2) and is expressed by the polynomial x2 + 6x + 8
(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8
In doing so, we can perform the inverse operation, namely, divide the area x2 + 6x + 8 by the width x + 2 and obtain the length x + 4.
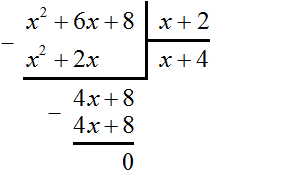
The power of a polynomial x2 + 6x + 8 is equal to the sum of powers of polynomials x + 4 and x + 2, so none of the powers of a polynomial can exceed the power of the product polynomial. Consequently, for inverse division to be possible, the power of the divisor must be less than the power of the dividend.
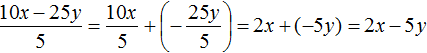
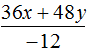
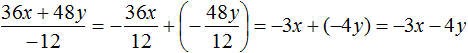
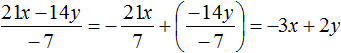
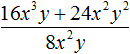
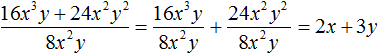
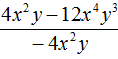
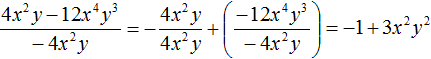
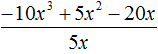
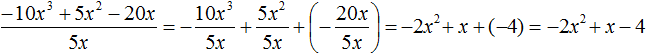
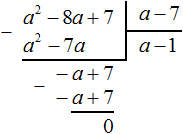
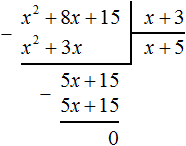
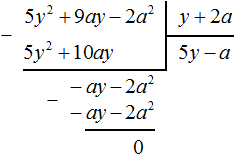
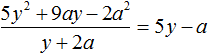
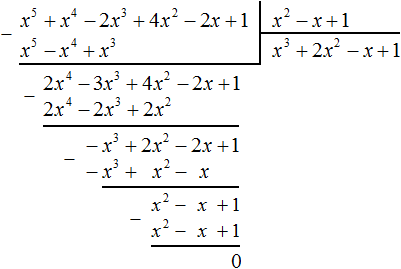
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.