Function y=k/x its properties and graph

In this lesson we will begin studying the graph of a function called a hyperbola. The function itself is called inverse proportionality. Not only mathematical problems are associated with this function, but also a number of problems, for example economics and physics. We will study the properties of this function, plot the graphs, and study the increasing and decreasing of the function.

, where:

 –  independent variable (argument);

 – dependent variable (function);

 – coefficient (number).

The graph of the function  is the set of points  where .

The coefficient  can take any values except . Let us first consider the case when ; thus, we will first deal with the function .

To plot the function , give the independent variable  some specific values and calculate (using a formula) the corresponding values of the dependent variable . We record the results in a table: one table for , another for .

Plot the found points , , , , on the coordinate plane  and connect them, thus obtaining the right branch of the graph (see Fig. 1).

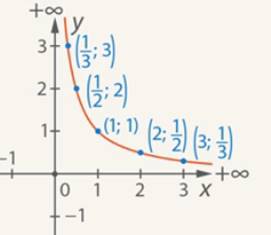
Fig. 1. The right branch of the graph

Plot the found points , , ,  on the coordinate plane  and connect them, thus obtaining the right branch of the graph (see Fig. 2).

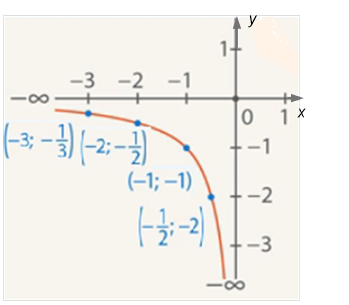
 Fig. 2. The left branch of the graph

Combine these two branches (see Fig. 3). This is the graph of the function ; it is called a hyperbola.

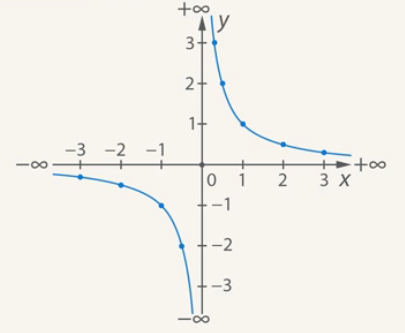
Fig. 3. The graph of the function  (hyperbola)

You can see that the graph consists of two parts. These parts are called branches of the hyperbola. 

1. For  (right branch):

- with  tending to plus infinity,  tends to zero:

, , hence, the -axis is the horizontal asymptote.

Asymptote (from Greek asimptotos - "non-conforming") is a line to which an infinite branch of a curve approaches indefinitely.

- with  tending to zero,  tends to plus infinity:

, , hence the -axis is a vertical asymptote.

For  (left branch):

- with  tending to minus infinity,  tends to zero:

, ,, hence the -axis is a horizontal asymptote.

- with  tending to zero,  tends to minus infinity:

, , hence the -axis is a vertical asymptote.

2. For  (right branch)

Take any two points  and , we obtain the segment  and the arc . The arc is under the segment, hence the function under study is convex downward at .

For  (left branch)

Take any two points  and , we obtain a segment  and an arc . The arc is above the segment, hence the function under study is convex upwards at  (see Fig. 4).

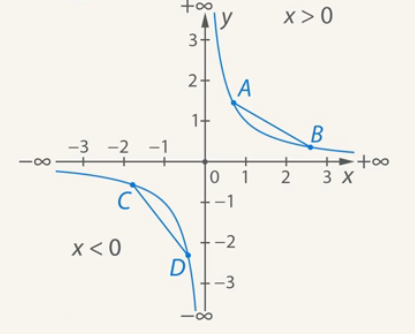
Fig. 4. Study of function

 Reminder

Axial symmetry (symmetry relative to a straight line)

Points  and  are symmetric with respect to line  if it serves as the median perpendicular to segment  (see Figure 5).

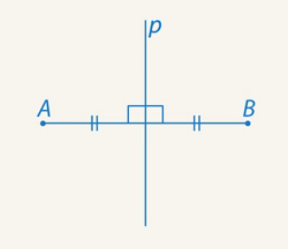
Fig. 5. Axial symmetry

Central symmetry (symmetry relative to the point)

Points  and  are symmetric with respect to point  if segment  is equal to segment  (see Fig. 6).

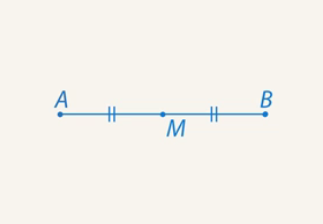
Fig. 6. Central symmetry

3. Draw the line . If we bend the graph of the function under study through this line, the branches will coincide. For example, the point  will coincide with the point . Consequently, the line  is the median perpendicular to the segment . Thus line  is the symmetry axis of the graph  (see Fig. 7).

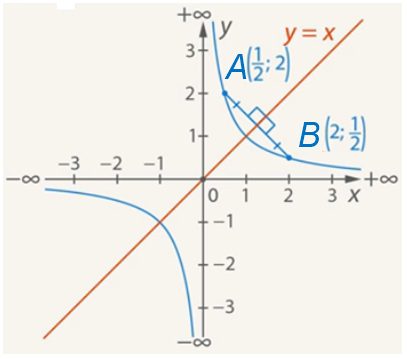
 Fig. 7. The symmetry axis of the hyperbola

4. The point with coordinates  is the center of symmetry of the graph .

We have considered the properties of the function , and the same properties will hold for the function   for any  (see Figure 8).

1. The area of the function is the set of all real numbers except .

2. The numbers  and  are of the same sign, therefore:

 at  

 at  

3. The function is bounded neither from below nor from above. This follows from the fact that 

4. At  the function decreases and is convex upwards; at  the function decreases and is convex downwards.

5. Point  is the center of symmetry of the hyperbola.

6. The straight  axis of symmetry of the hyperbola.

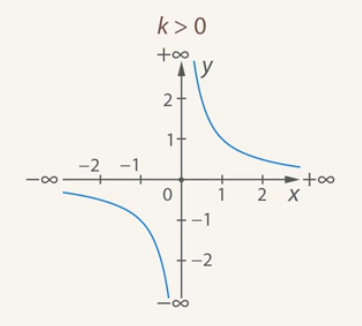
Fig. 8. The graph of the function  at 

Proof of axial symmetry of the hyperbola

The graph of the function .

1. Let  be any value of the argument from the definition area. Then on the branch of the hyperbola we have point .

2. Let  be any value of the argument from the definition area. Then we have point  on the branch of the hyperbola.

It is necessary to prove that an arbitrarily chosen point  is symmetric to point  with respect to line  (see Fig. 9).

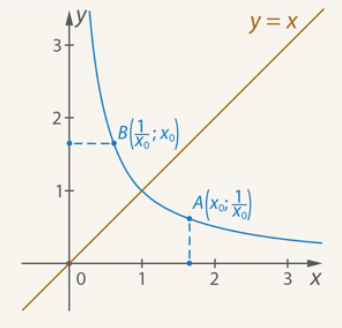
 Figure 9. Illustration of the proof

Proof

1. Mark the point  on the abscissa axis and the point  on the ordinate axis (see Fig. 10).

2. Consider right triangles  and . These triangles are equal by two cathetuses (; ). It follows from the equality of these triangles:

а) ;

b) ;

с)  (since line  is the bisector of the coordinate angle, and )

3. Consider triangle : it is isosceles, the line  lies on the bisector of the triangle. It is known that in an isosceles triangle the bisector originating from the angle formed by equal sides is also the altitude and the median. Hence, line  is the median perpendicular to the segment ; arbitrarily chosen point  is symmetric to the point  with respect to the line .

Since the points were chosen arbitrarily, the entire curve  is symmetric about the .

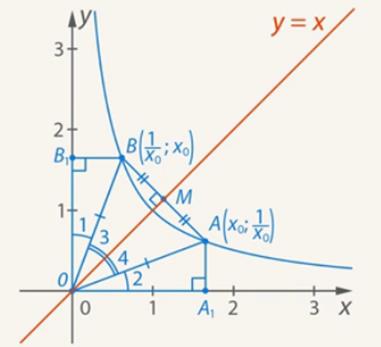
 Figure 10. illustration of the proof

At , the branches of the hyperbola are located in the second and fourth coordinate angles (see Fig. 11).

1. The domain of the function is the set of all real numbers except .

2. The numbers  and  are different signs, therefore:

 at  

 at  

3. The function is not limited either from below or from above.

4. At , the function increases and is convex downward; at , the function increases and is convex upward.

5. Point  is the center of symmetry of the hyperbola.

6. The straight  axis of symmetry of the hyperbola.

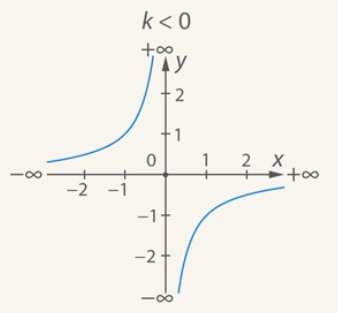
Fig. 11. The graph of the function  at