In this lesson we will study addition and subtraction of integers.
Recall that integers are all positive and negative numbers, as well as the number 0.
For example, the following numbers are integers:
−3, −2, −1, 0, 1, 2, 3
It is easy to add and subtract, multiply and divide positive numbers. Unfortunately, the same cannot be said for negative numbers, which confuse many beginners with their minuses before each digit.
Examples of addition and subtraction of integers
The first thing to learn is how to add and subtract integers using a coordinate line. It is not necessary to draw a number line. It is enough to imagine it in your mind and see where the negative numbers are and where the positive numbers are.
Consider the following simple expression
1 + 3
The value of this expression is 4
1 + 3 = 4
This example can be understood using a number line. To do this, from the point where the number 1 is located, we have to move three steps to the right. This will bring us to the point where the number 4 is located. You can see how this happens in the picture:
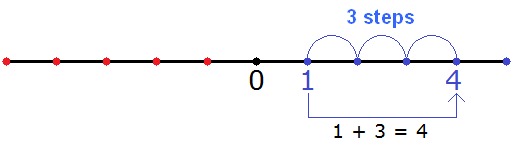
The plus sign in the expression 1 + 3 tells us to move to the right to increase the numbers.
Example 2. Find the value of the expression 1 - 3
The value of this expression is -2
1 − 3 = −2
This example can again be understood using a coordinate line. To do this, from the point where the number 1 is located, we have to move three steps to the left. As a result, we end up at the point where the negative number -2 is located. You can see in the picture how this happens:

The minus sign in the expression 1 - 3 tells us to move to the left to decrease the numbers.
In general, if you are adding, you should move to the right side of the number line. If subtraction is performed, then we must move to the left toward the decreasing side.
Example 3. Find the value of the expression -2 + 4
The value of this expression is 2
−2 + 4 = 2
Again, this example can be understood using a number line. To do this, from the point where the negative number -2 is located, we need to move to the right by four steps. This will bring us to the point where the positive number 2 is located.
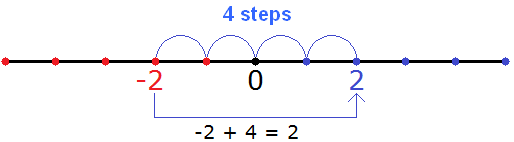
You can see that we moved from the point where the negative number -2 is located to the right side by four steps, and ended up at the point where the positive number 2 is located.
Example 4. Find the value of the expression -1 - 3
The value of this expression is -4
−1 − 3 = −4
Again, this example can be solved using a coordinate line. To do this, from the point where the negative number -1 is located, move to the left by three steps. As a result, we will find ourselves at the point where the negative number -4 is located.
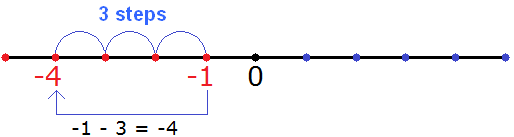
You can see that we moved from the point where there is a negative number -1 to the left side by three steps, and ended up at the point where there is a negative number -4.
Example 5. Find the value of the expression -2 + 2
The value of this expression is 0
−2 + 2 = 0
This example can be solved using a coordinate line. From the point where the negative number -2 is located, move two steps to the right. As a result, we will find ourselves at the point where the number 0
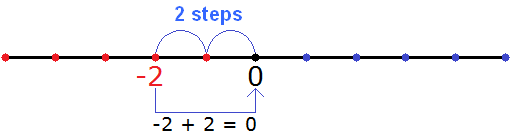
You can see that we have moved from the point where the negative number -2 is located to the right side by two steps and ended up at the point where the number 0 is located.
Rules for addition and subtraction of integers
To add or subtract integers, you don't have to imagine a number line every time. It is possible to use ready-made rules.
When applying the rules, you need to pay attention to the sign of the operation and the signs of the numbers to be added or subtracted. This will determine which rule to apply.
Example 1. Find the value of the expression -2 + 5
Here a positive number is added to a negative number. In other words, numbers with different signs are added, because -2 is a negative number, and 5 is a positive number. The following rule applies to such cases:
To add numbers with different signs, subtract the smaller modulus from the larger modulus, and precede the answer with the sign of the number whose modulus is greater.
So, let's see which module is bigger:
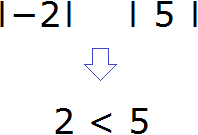
The modulus of 5 is greater than the modulus of -2. The rule requires that the greater modulus be subtracted from the lesser modulus. So we must subtract 2 from 5, and put the sign of the number whose modulus is greater in front of the answer.
Number 5 has a greater modulus, so the sign of this number will be in the answer. That is, the answer will be positive:
−2 + 5 = 5 − 2 = 3
Usually written in shorter form: -2 + 5 = 3
Example 2. Find the value of the expression 3 + (-2)
Here, as in the previous example, numbers with different signs are added. 3 is a positive number and -2 is a negative number. Note that the number -2 is put in parentheses to make the expression clearer. This expression is much easier to understand than the expression 3 + -2.
So let's apply the rule of adding numbers with different signs. As in the previous example, we subtract the smaller modulus from the larger modulus and put the sign of the number whose modulus is larger in front of the answer:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
The modulus of number 3 is greater than the modulus of number -2, so we subtracted 2 from 3, and put the sign of the number whose modulus is greater before the answer. Number 3 has a greater modulus, so we put the sign of that number in the answer. That is, the answer is positive.
Usually write shorter 3 + (-2) = 1
Example 3. Find the value of the expression 3 - 7
In this expression, the greater number is subtracted lesser number. The following rule applies to this case:
To subtract a greater number from other number, you must subtract a lesser number from a greater number and put a minus sign in front of the answer.
3 − 7 = 7 − 3 = −4
There is a small catch in this expression. Recall that an equal sign (=) is placed between values and expressions when they are equal to each other.
The value of the expression 3 - 7 as we have learned is -4. This means that any transformations we will perform in this expression must equal -4
But we can notice that in the second step there is an expression 7 - 3, which is not equal to -4.
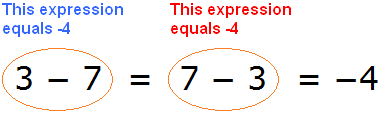
To fix this, the expression 7 - 3 must be placed in parentheses and a minus must be placed before this bracket:
3 − 7 = − (7 − 3) = − (4) = −4
In this case, equality will be observed at every stage:
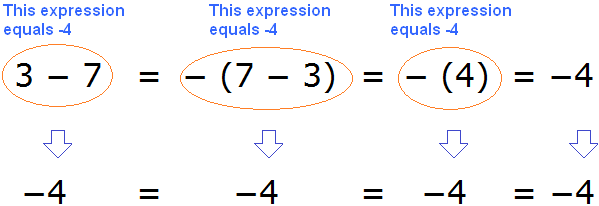
After the expression is calculated, the parentheses can be removed, which we did.
Therefore, to be more accurate, the solution should look like this:
3 − 7 = − (7 − 3) = − (4) = − 4
This rule can be written using variables. It looks as follows:
a − b = − (b − a)
A large number of parentheses and operation signs can complicate the solution of a seemingly simple problem, so it is better to learn to write such examples briefly, e.g., 3 - 7 = - 4.
In fact, adding and subtracting integers is all about addition. This means that if subtraction of numbers is required, this operation can be replaced by addition.
So, let's learn a new rule:
To subtract number b from a means to add opposite b (-b) to a.
For example, consider the simplest expression 5 - 3. In the early stages of mathematics, we used to put an equal sign and write down the answer:
5 − 3 = 2
But now we are making progress in learning, so we have to adjust to the new rules.
Using the expression 5 - 3 as an example, let's try to understand this rule. The minuend in this expression is 5, and the subtrahend is 3. The rule says that in order to subtract 3 from 5, you must add a number that is the opposite of 3 to 5. The opposite of 3 is -3. Write down the new expression:
5 + (−3)
And we already know how to find values for such expressions. This is the addition of numbers with different signs, which we discussed earlier. To add numbers with different signs, we subtract the smaller modulus from the larger modulus, and put the sign of the number whose modulus is larger in front of the answer:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
The modulus of 5 is greater than the modulus of -3. So we subtracted 3 from 5 and got 2. The modulus of 5 is greater, so we put the sign of that number in the answer. That is, the answer is positive.
At first, not everyone is able to quickly replace subtraction with addition. This is because positive numbers are written without a plus sign.
For example, in the expression 3 - 1, the minus sign indicating subtraction is an operation sign and does not refer to a unit. The unit in this case is a positive number, and it has its own plus sign, but we do not see it because the plus sign is not written in front of positive numbers.
And therefore, for clarity, this expression can be written as follows:
(+3) − (+1)
For convenience, numbers with their signs are enclosed in parentheses. In this case it is much easier to replace the subtraction with addition.
In the expression (+3) - (+1), the number to be subtrahend is (+1), and the opposite number is (-1).
Replace the subtraction with addition, and instead of the subtracted number (+1), write the opposite number (-1).
(+3) − (+1) = (+3) + (−1)
Further calculation is not too difficult.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
At first glance, it may seem that there is no sense in these extra steps if you can use the good old method to put an equal sign and immediately write down the answer 2. In fact, this rule will help us more than once.
Let's solve the previous example 3 - 7 using the subtraction rule. First, let's make the expression understandable by placing each number with its own signs.
The three has a plus sign because it is a positive number. The minus sign indicating subtraction does not apply to the seven. Seven has a plus sign because it is a positive number:
(+3) − (+7)
Replace subtraction with addition:
(+3) − (+7) = (+3) + (−7)
Further calculation is not difficult:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Example 7. Find the value of the expression -4 - 5
Let's reduce the expression to a comprehensible form:
(−4) − (+5)
This is again a subtraction operation. This operation must be replaced by addition. To the subtractor (-4) add the number opposite to the subtractor (+5). The opposite number to the subtractor (+5) is (-5).
(−4) − (+5) = (−4) + (−5)
We come to a situation where we need to add negative numbers. For such cases the following rule applies:
To add negative numbers, sum up both modulus and put minus in front of the result.
So let's add the both modulus of the numbers, as required by the rule, and put minus in front of the answer:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
The entry with modules should be put in parentheses and a minus in front of those parentheses. In this way we will provide the minus that must come before the answer:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
The solution for this example can be written in a shorter form:
−4 − 5 = −(4 + 5) = −9
or even shorter:
−4 − 5 = −9
Example 8. Find the value of the expression −3 − 5 − 7 − 9
Let's reduce the expression to an understandable form. Here all numbers except -3 are positive, so they will have plus signs:
(−3) − (+5) − (+7) − (+9)
Replace subtraction with addition. All minuses except the minus in front of the three will change to pluses, and all positive numbers will change to opposites:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Now apply the rule of adding negative numbers. To add negative numbers, add their moduli and put a minus in front of the answer:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
The solution to this example can be written in a shorter form:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
or even shorter:
−3 − 5 − 7 − 9 = −24
Example 9. Find the value of the expression −10 + 6 − 15 + 11 − 7
Let's reduce the expression to a comprehensible form:
(−10) + (+6) − (+15) + (+11) − (+7)
Here we have two operations at once: addition and subtraction. We leave addition unchanged and replace subtraction with addition:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Observing the order of operations, perform each action in turn, based on the rules you learned earlier. You can skip the entries with modules:
First action:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Second action:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Third action:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Fourth action:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Thus, the value of the expression -10 + 6 - 15 + 11 - 7 equals -15
Note. It is not necessary to make an expression understandable by putting numbers in parentheses. When you get used to negative numbers, you can skip this action because it is time-consuming and can be confusing.
So, to add and subtract integers, you need to remember the following rules:
1. To add numbers with different signs, subtract the smaller modulus from the larger modulus, and precede the answer with the sign of the number whose modulus is greater.
2. To subtract a larger number from a smaller number, subtract a smaller number from a larger number and put a minus in front of the answer.
3. Subtracting one number from another means adding to the subtractor a number that is the opposite of the subtractor.
4. To add negative numbers, add their modulus and put minus in front of the answer.
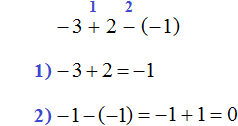
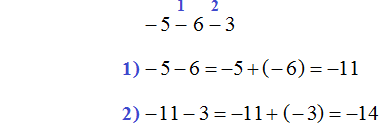
Comments