We continue to study elementary math tasks. This lesson is about fractions.
Before solving fraction tasks, you should thoroughly study all of the topics related to fractions. Below is a list of lessons that can be repeated.
Each task in this lesson belongs to the elementary category. If you do not understand any of the tasks, it is an indication that the previous material is not well understood.
Tasks on fractions
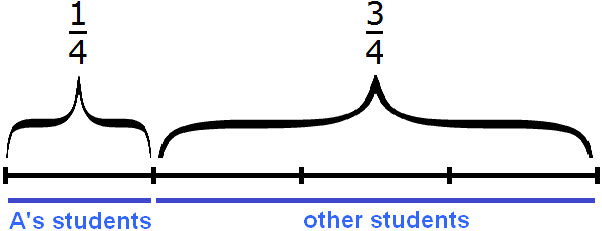
Task 1. One-quarter of the class is A's students. What part of the class are the rest of them?
Solution
If ![]() are A's students, then
are A's students, then ![]() are the others.
are the others.
Task 2. ![]() of the students are straight A's,
of the students are straight A's, ![]() are B's, and
are B's, and ![]() are C's. Make a simple drawing describing it.
are C's. Make a simple drawing describing it.

Task 3. There are 24 students in the class. ![]() of the students are straight A's,
of the students are straight A's, ![]() are B's, and
are B's, and ![]() are C's. How many excellent, good and bad students are there in the class?
are C's. How many excellent, good and bad students are there in the class?
Solution
24 : 6 × 1 = 4 × 1 = 4 (A's)
24 : 6 × 3 = 4 × 3 = 12 (B's)
24 : 6 × 2 = 4 × 2 = 8 (C's)
Check
4 + 12 + 8 = 24 (student)
24 = 24
Task 4. ![]() of the class is made up of A's, and
of the class is made up of A's, and ![]() are B's. What fraction represents C's students?
are B's. What fraction represents C's students?
Solution
Students are divided into six parts. The A's are in one part, the B's in three parts. It's not hard to guess that the remaining two parts are made up of the C's. So ![]() of students are C's.
of students are C's.

Without giving figures, you can add the fractions ![]() and
and ![]() , and subtract the result from the fraction
, and subtract the result from the fraction ![]() , which expresses the whole part of the students. In other words, add up the A's and B's, then subtract these A's and B's from the total number of students
, which expresses the whole part of the students. In other words, add up the A's and B's, then subtract these A's and B's from the total number of students

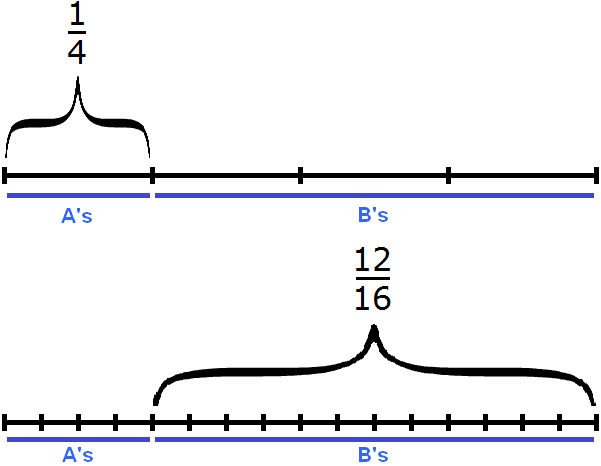
Task 5. There are 16 students in the class. ![]() of them are A's and
of them are A's and ![]() are B's. How many A's and B's students are there in the class? Make a simple figure which describes it best
are B's. How many A's and B's students are there in the class? Make a simple figure which describes it best
Solution
16 : 4 × 1 = 4 × 1 = 4 (A's)
16 : 16 × 12 = 1 × 12 = 12 (B's)
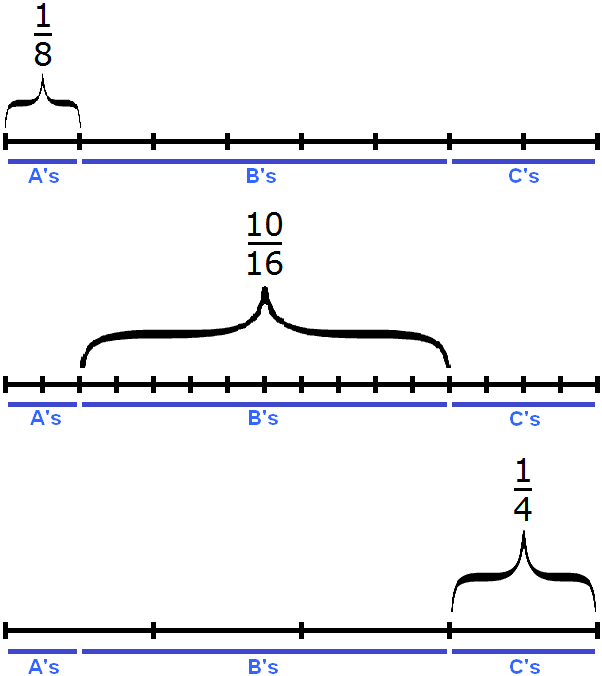
Task 6. There are 16 students in the class. Of those, ![]() are A's,
are A's, ![]() are B's, and
are B's, and ![]() are C's. How many A's, B's, and C's students in the class?
are C's. How many A's, B's, and C's students in the class?
Solution
16 : 8 × 1 = 2 × 1 = 2 (A's)
16 : 16 × 10 = 1 × 10 = 10 (B's)
16 : 4 = 4 (C's)
Task 7. Wheat is used to produce groats, the mass of which is ![]() of the weight of the wheat, and the rest is fodder waste. How much groats and fodder waste can be obtained from 500 quintals of wheat
of the weight of the wheat, and the rest is fodder waste. How much groats and fodder waste can be obtained from 500 quintals of wheat
Solution
Let's find ![]() of 500 quintals:
of 500 quintals:
![]()
Now let's find the mass of feed waste. To do this, subtract the mass of groats from 500 quintals:
![]()
So from 500 quintals of wheat you can get 320 quintals of groats and 180 quintals of feed waste.
Task 8: A kilogram of crab meat costs $88. How much is ![]() kilogram of crab meat?
kilogram of crab meat? ![]() kg?
kg? ![]() kg?
kg? ![]() kg?
kg?
Solution
1) ![]() kg is half of one kilogram. If one kilogram costs $88, then half a kilogram will cost half of $88, which is $44. If we find half of $88, we get $44.
kg is half of one kilogram. If one kilogram costs $88, then half a kilogram will cost half of $88, which is $44. If we find half of $88, we get $44.
88 : 2 = 44
44 × 1 = $44
2) ![]() kg is a quarter of a kilogram. If one kilogram costs $88, then a quarter of a kilogram will cost a quarter of $88, i.e. $22. If we find
kg is a quarter of a kilogram. If one kilogram costs $88, then a quarter of a kilogram will cost a quarter of $88, i.e. $22. If we find ![]() of $88, we get $22.88 : 4 = 22
of $88, we get $22.88 : 4 = 22
22 × 1 = $22
3) Fraction ![]() means that a kilogram is divided into eight parts, and three parts are taken from there. If one kilogram costs $88, then the cost of three eight kilograms will be 3/8 of $88. If we find
means that a kilogram is divided into eight parts, and three parts are taken from there. If one kilogram costs $88, then the cost of three eight kilograms will be 3/8 of $88. If we find ![]() of $88, we get $33.
of $88, we get $33.
4) The fraction ![]() means that a kilogram is divided into eight parts, and eleven parts are taken from there. But it is impossible to take eleven parts if there are only eight parts. We are dealing with an improper fraction. First, let's isolate the whole part in it:
means that a kilogram is divided into eight parts, and eleven parts are taken from there. But it is impossible to take eleven parts if there are only eight parts. We are dealing with an improper fraction. First, let's isolate the whole part in it:
![]()
![]() is one whole kilogram and
is one whole kilogram and ![]() of a kilogram. Now we can separately find the cost of one whole kilogram and the cost of three eighths of a kilogram. One kilogram, as stated above, costs $88. We also found the cost of
of a kilogram. Now we can separately find the cost of one whole kilogram and the cost of three eighths of a kilogram. One kilogram, as stated above, costs $88. We also found the cost of ![]() ths of a kilogram earlier and got $33. So
ths of a kilogram earlier and got $33. So ![]() kg of crab meat would cost $88+33 dollars, which is $121.
kg of crab meat would cost $88+33 dollars, which is $121.
The cost of ![]() can be found without singling out the whole part. To do this, just find
can be found without singling out the whole part. To do this, just find ![]() from 88 (Lesson - Finding fractions from a number).
from 88 (Lesson - Finding fractions from a number).
88 : 8 = 11
11 × 11 = 121
But highlighting the whole part you can well understand how the price of ![]() kg of crab meat was formed.
kg of crab meat was formed.
Task 9: A substance contain ![]() sugar and
sugar and ![]() mineral salts. How many grams of each substance are contained in 4 kg of a substance?
mineral salts. How many grams of each substance are contained in 4 kg of a substance?
Solution
Let's find out how many grams of sugar are in one kilogram of dates. One kilogram is one thousand grams. Find ![]() of 1000 grams:
of 1000 grams:
1000 : 25 = 40
40 × 18 = 720 g
One kilogram of dates contains 720 grams of sugar. To find out how many grams of sugar are in four kilograms, multiply 720 by 4.
720 × 4 = 2880 g
Now let's find out how many mineral salts are in 4 kilograms of dates. But first, let's find out how many mineral salts are in one kilogram. One kilogram is a thousand grams. Find ![]() of 1000 grams:
of 1000 grams:
1000 : 200 = 5
5 × 3 = 15 g
One kilogram of dates contains 15 grams of mineral salts. To find out how many grams of mineral salts are in four kilograms, multiply 15 by 4.
15 × 4 = 60 g
So 4 kg of dates contains 2880 grams of sugar and 60 grams of mineral salts.
The solution to this problem can be written in much shorter form, in two expressions:
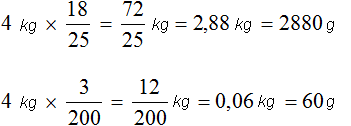
The point is that they found ![]() from 4 kilograms and converted the resulting 2.88 to grams by multiplying by 1000. The same was done for mineral salts - from 4 kg we found
from 4 kilograms and converted the resulting 2.88 to grams by multiplying by 1000. The same was done for mineral salts - from 4 kg we found ![]() and the resulting kilograms were converted to grams by multiplying by 1000. Note also that the fraction of a number was found in a simplified way - by direct multiplication of the number by the fraction.
and the resulting kilograms were converted to grams by multiplying by 1000. Note also that the fraction of a number was found in a simplified way - by direct multiplication of the number by the fraction.
Task 10. The train has covered 840 km, which is ![]() of its way. What distance does it have left to travel? What is the distance of the entire trip?
of its way. What distance does it have left to travel? What is the distance of the entire trip?
Solution
The task states that 840 km is ![]() of his path. The denominator of the fraction
of his path. The denominator of the fraction ![]() indicates that the whole path is divided into seven equal parts, and the numerator indicates that four parts of this path have already been traveled and are 840 km. Therefore, by dividing 840 km by 4, we will know how many kilometers are in one part:
indicates that the whole path is divided into seven equal parts, and the numerator indicates that four parts of this path have already been traveled and are 840 km. Therefore, by dividing 840 km by 4, we will know how many kilometers are in one part:
840 : 4 = 210 km.
And since the entire path consists of seven parts, the distance of the entire path can be found by multiplying 210 by 7:
210 × 7 = 1470 km.
Now answer the second question of the task - how much distance does the train have left to cover? If the distance is 1470 km, and 840 km have passed, then the remaining distance is 1470 - 840, i.e. 630
1470 − 840 = 630
Task 11. One of the groups that conquered Everest consisted of athletes, guides, and porters. There were 25 sportsmen in the group, the number of guides was ![]() of the number of sportsmen, and the number of sportsmen and guides together was only
of the number of sportsmen, and the number of sportsmen and guides together was only ![]() of the number of porters. How many porters were there on this expedition?
of the number of porters. How many porters were there on this expedition?
Solution
Sportsmen in the group of 25. The guides are ![]() of the number of sportsmen. Find
of the number of sportsmen. Find ![]() of 25 and find out how many guides there are in the group:
of 25 and find out how many guides there are in the group:
25 : 5 × 4 = 20
The sportsmen and guides together are 45 people. This number is ![]() of the number of porters. Knowing that
of the number of porters. Knowing that ![]() of the number of porters is 45 people, we can find the total number of porters. To do this, we will find the number by fractions:
of the number of porters is 45 people, we can find the total number of porters. To do this, we will find the number by fractions:
45 : 9 × 140 = 5 × 140 = 700
Task 12. The school received 900 new textbooks, of which math textbooks were ![]() of all books, English textbooks
of all books, English textbooks ![]() of all books, and the rest were literature books. How many literature books were brought in?
of all books, and the rest were literature books. How many literature books were brought in?
Let's find out how many math textbooks make up:
900 : 25 × 8 = 288 (math books)
Let's find out how many English textbooks:
900 : 100 × 33 = 297 (English books)
Let's find out how many books on literature. We'll subtract the math and English textbooks from the total number of books:
900 – (288+297) = 900 – 585 = 315
Check
288 + 297 + 315 = 900
900 = 900
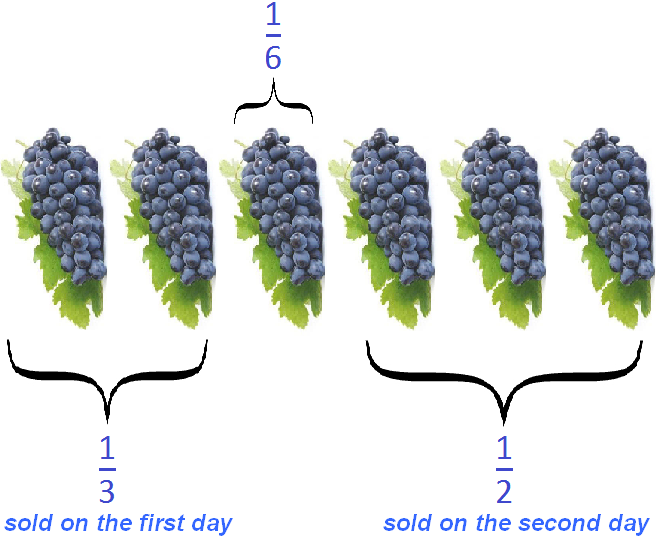
Task 13. On the first day they sold ![]() and on the second day
and on the second day ![]() of the grapes that came into the store. How many grapes were sold in two days?
of the grapes that came into the store. How many grapes were sold in two days?
Solution
In two days they sold ![]() of the grapes. This fraction is obtained by adding fractions
of the grapes. This fraction is obtained by adding fractions ![]() and
and ![]()
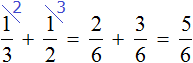
You can imagine the grapes that came to the store as six bunches. Then ![]() of grapes is two bunches,
of grapes is two bunches, ![]() of grapes is three bunches, and
of grapes is three bunches, and ![]() of grapes is five bunches of six sold in two days. Well, it is not difficult to see that there is one bunch left, expressed as a fraction of
of grapes is five bunches of six sold in two days. Well, it is not difficult to see that there is one bunch left, expressed as a fraction of ![]() (one bunch of six grapes).
(one bunch of six grapes).
Task 14. The girl read ![]() of the book on the first day and
of the book on the first day and ![]() less on the second day. How much of the book did the girl read on the second day? Did she manage to read the book in two days?
less on the second day. How much of the book did the girl read on the second day? Did she manage to read the book in two days?
Solution
Determine the part of the book read on the second day. It is said that ![]() less was read on the second day than on the first day.
less was read on the second day than on the first day.
Therefore, you must subtract ![]() from
from ![]() .
.
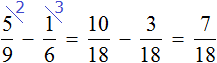
On the second day, the girl read ![]() books. Now let's answer the second question of the problem: Did the girl manage to read the book in two days? Add up what the girl read on day one and day two:
books. Now let's answer the second question of the problem: Did the girl manage to read the book in two days? Add up what the girl read on day one and day two:
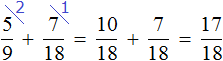
The girl has read ![]() books in two days, but there is still
books in two days, but there is still ![]() books left. So the girl did not have time to read the whole book in two days.
books left. So the girl did not have time to read the whole book in two days.
Let's do a test. Suppose the book the girl was reading had 180 pages. On the first day she read ![]() of the book. Find
of the book. Find ![]() of 180 pages.
of 180 pages.
180 : 9 × 5 = 100 (pages)
On the second day, the girl read ![]() less than on the first day. Let's find
less than on the first day. Let's find ![]() of 180 pages and subtract the result from 100 pages read on the first day.
of 180 pages and subtract the result from 100 pages read on the first day.
180 : 6 × 1 = 30 × 1 = 30 (pages)
100 − 30 = 70 (pages on the second day)
Let's see if the 70 pages ![]() are part of the book:
are part of the book:
180 : 18 × 7 = 10 × 7 = 70 (pages)
Now let's answer the second question of the problem - did the girl manage to read all 180 pages in two days. The answer is no, because she read only 170 pages in two days.
100 + 70 = 170 (pages)
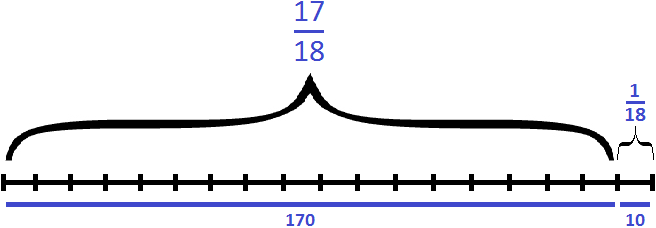
There are ten more pages to read. In the task, we had the fraction ![]() as the remainder. Let's check if the 10 pages of
as the remainder. Let's check if the 10 pages of ![]() are part of the book?
are part of the book?
180 : 18 × 1 = 10 × 1 = 10 (pages)
Task 15. One bag has ![]() kg of candy and the other has
kg of candy and the other has ![]() kg less. How many kilograms of candy are in the two bags together?
kg less. How many kilograms of candy are in the two bags together?
Solution
Determine the mass of the second package. It is ![]() of a kilogram less than the mass of the first package. Therefore we subtract the mass of the second package from the mass of the first package:
of a kilogram less than the mass of the first package. Therefore we subtract the mass of the second package from the mass of the first package:
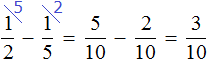
The mass of the second package is ![]() kg. Determine the mass of both packages. Add the mass of the first and the mass of the second:
kg. Determine the mass of both packages. Add the mass of the first and the mass of the second:
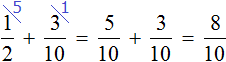
The weight of both bags is ![]() kilograms. And
kilograms. And ![]() of a kilogram is 800 grams. You can solve such a problem by working with fractions, adding and subtracting them. You can also first find the number using the fractions in the problem and begin to solve it. So
of a kilogram is 800 grams. You can solve such a problem by working with fractions, adding and subtracting them. You can also first find the number using the fractions in the problem and begin to solve it. So ![]() of a kilogram is 500 grams, and
of a kilogram is 500 grams, and ![]() of a kilogram is 200 grams.
of a kilogram is 200 grams.
1000 : 2 × 1 = 500 × 1 = 500 g
1000 : 5 × 1 = 200 × 1 = 200 g
The second bag has 200 grams less, so to determine the mass of the second bag, subtract 200 grams from 500 g
500 − 200 = 300 g
And then add up the masses of both packages:
500 + 300 = 800 g
Task 16. The tourists walked from the camping to the lake in four days. On the first day they walked ![]() of the way, on the second day they walked
of the way, on the second day they walked ![]() of the rest of the way, and on the third and fourth days they walked 12 km each. What is the distance from the camping to the lake?
of the rest of the way, and on the third and fourth days they walked 12 km each. What is the distance from the camping to the lake?
Solution
The task says that on the second day, the tourists walked ![]() of the rest of the distance. A fraction of
of the rest of the distance. A fraction of ![]() means that the remaining distance is divided into 7 equal parts, of which the tourists have walked three parts, but the remaining
means that the remaining distance is divided into 7 equal parts, of which the tourists have walked three parts, but the remaining ![]() parts are left to walk. On these
parts are left to walk. On these ![]() accounts for the distance that tourists walked on the third and fourth day, that is, 24 km (12 km on each day). Let's draw a visual diagram illustrating the second, third, and fourth days:
accounts for the distance that tourists walked on the third and fourth day, that is, 24 km (12 km on each day). Let's draw a visual diagram illustrating the second, third, and fourth days:
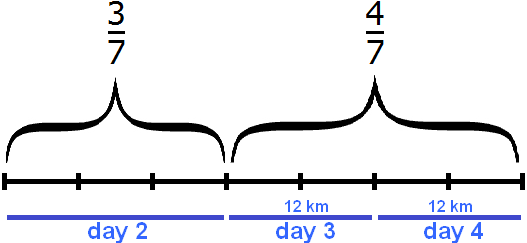
On the third and fourth day, the tourists walked 24 km, which is ![]() of the distance walked on the second, third, and fourth days. Knowing that
of the distance walked on the second, third, and fourth days. Knowing that ![]() is 24 km, we can find the total distance traveled on the second, third, and fourth days:
is 24 km, we can find the total distance traveled on the second, third, and fourth days:
24 : 4 × 7 = 6 × 7 = 42 km
On the second, third and fourth day the tourists walked 42 km. Now find ![]() of that distance. So we will know how many kilometers the tourists walked on the second day:
of that distance. So we will know how many kilometers the tourists walked on the second day:
42 : 7 × 3 = 6 × 3 = 18 km
Now back to the beginning of the task. We say that on the first day the tourists walked ![]() of the way. The whole path is divided into four parts, and the first part is the path covered on the first day. And the path, which accounts for the remaining three parts, we have already found - it is 42 kilometers covered in the second, third, and fourth days. Let's draw a visual scheme illustrating the first and the other three days:
of the way. The whole path is divided into four parts, and the first part is the path covered on the first day. And the path, which accounts for the remaining three parts, we have already found - it is 42 kilometers covered in the second, third, and fourth days. Let's draw a visual scheme illustrating the first and the other three days:
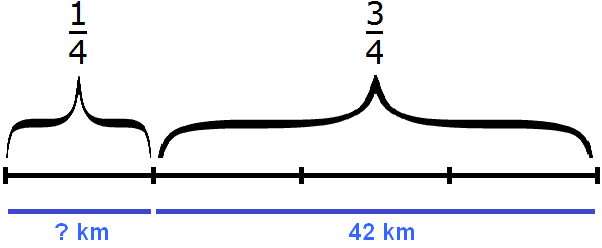
Knowing that ![]() of the way is 42 kilometers, we can find the length of the entire path:
of the way is 42 kilometers, we can find the length of the entire path:
42 : 3 × 4 = 56 km
So the length of the path from the camping site to the lake is 56 kilometers. Let's check. To do this, add up all the paths traveled by the tourists on each of the four days.
First, let's find the distance traveled on the first day:
56 : 4 × 1 = 14 (on the first day).
14 + 18 + 12 + 12 = 56
56 = 56
A task from the arithmetic of the famous Central Asian mathematician Muhammad ibn-Musa al-Khwarizmi (IX century A.D.)
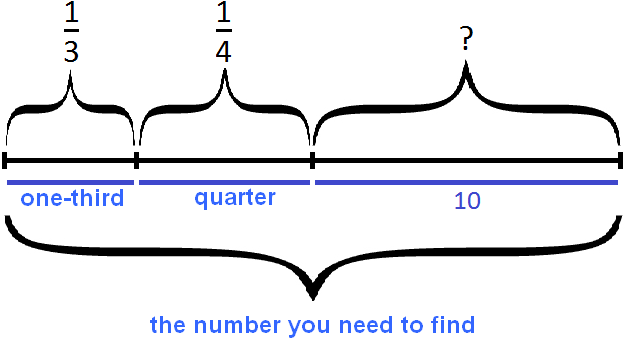
"Find a number knowing that if you subtract one third and one quarter from it, you get 10."
Let's represent the number we want to find as a segment divided into three parts. In the first part of the segment mark a third, in the second part mark a quarter, the remaining third part will represent the number 10.
Let's add a third and a quarter:
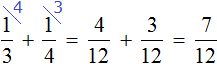
Now draw a segment divided into 12 parts. Mark on it the fraction ![]() , the remaining five parts go to the number 10:
, the remaining five parts go to the number 10:
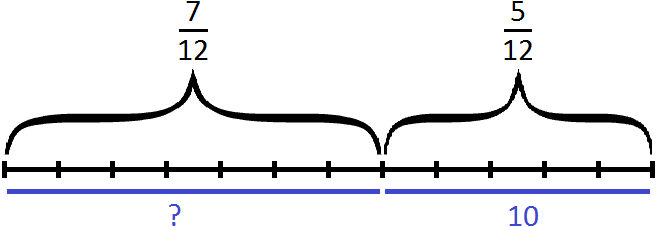
Knowing that 5/12 of a number make up the number 10, we can find the whole number:
10 : 5 × 12 = 2 × 12 = 24
We have found the whole number - it is 24.
This problem can be solved without using pictures. To do this, first add a third and a quarter. Then subtract the result of adding one-third and one-quarter from one, which we have an unknown number. Then use the resulting fraction to determine the whole number:
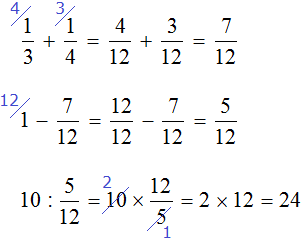
Task 17. The family consists of 5 people. Mom and Dad earn $200,000 a year. The budget is budgeted as follows: ![]() for food,
for food, ![]() for utilities,
for utilities, ![]() for Internet, mobile, entertainment and TV,
for Internet, mobile, entertainment and TV, ![]() for medical expenses,
for medical expenses, ![]() for charity,
for charity, ![]() for home rent,
for home rent, ![]() for the piggy bank. How much money is allocated for food, utilities, Internet and TV, medical expenses, charity, home rent, and piggy bank?
for the piggy bank. How much money is allocated for food, utilities, Internet and TV, medical expenses, charity, home rent, and piggy bank?
Solution
200 : 40 × 7 = 35 K (for food)
200 : 20 × 1 = 10 × 1 = 10 K (for utilities)
200 : 20 × 1 = 10 × 1 = 10 K (for Internet, mobile, entertainment and TV)
200 : 20 × 3 = 10 × 3 = 30 K (for medical expenses)
200 : 10 × 1 = 20 × 1 = 20 K (for charity)
200 : 20 × 3 = 10 × 3 = 30 K (for home rent)
200 : 40 × 13 = 5 × 13 = 65 K (for piggy bank)
Check
35 + 10 + 10 + 30 + 20 + 30 + 65 = 200
200 = 200
Task 18. The tourists walked ![]() km in the first hour, and
km in the first hour, and ![]() km more in the second hour. How many kilometers did the tourists walk in two hours?
km more in the second hour. How many kilometers did the tourists walk in two hours?
Solution
Let's find the numbers by fractions. ![]() is three whole kilometers and seven tenths of a kilometer, and seven tenths of a kilometer is 700 meters:
is three whole kilometers and seven tenths of a kilometer, and seven tenths of a kilometer is 700 meters:
![]()
![]() is one whole kilometer and one fifth of a kilometer, and one fifth of a kilometer is 200 meters
is one whole kilometer and one fifth of a kilometer, and one fifth of a kilometer is 200 meters
![]()
Determine the length of the path walked by the tourists in the second hour. This is done by adding 1 km 200 m to 3 km 700 m.
3 km 700m + 1 km 200m = 3700m + 1200m = 4900m = 4 km 900m.
How long was the distance traveled by the tourist in two hours?
3 km 700m + 4 km 900m = 3700m + 4900m = 8600m = 8 km 600m
So, in two hours the tourists walked 8 km and another 600 m. Let us solve this task with fractions. This way it can be shortened considerably
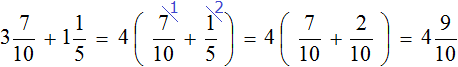
![]()
The answer is ![]() of a kilometer. That's eight whole kilometers and six tenths of a kilometer, and six tenths of a kilometer is six hundred meters
of a kilometer. That's eight whole kilometers and six tenths of a kilometer, and six tenths of a kilometer is six hundred meters
![]()
Task 19. Geologists walked a valley located between mountains in three days. On the first day they walked ![]() of the way, on the second
of the way, on the second ![]() of the way, and on the third the remaining 28 km. Calculate the length of the path through the valley.
of the way, and on the third the remaining 28 km. Calculate the length of the path through the valley.
Solution
Let's represent the path as a segment divided into three parts. In the first part mark ![]() of the way, in the second part
of the way, in the second part ![]() of the way, in the third part the remaining 28 kilometers:
of the way, in the third part the remaining 28 kilometers:
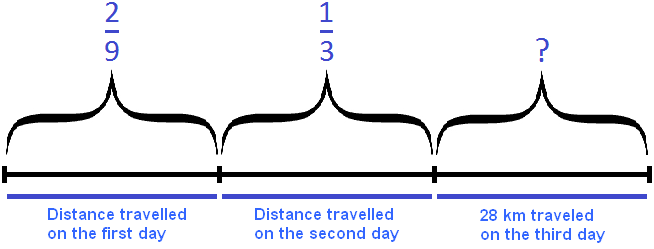
Let's add up the parts of the path taken on day one and day two:
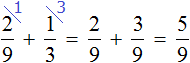
On the first and second days, the geologists walked ![]() of the entire route. The remaining
of the entire route. The remaining ![]() of the path is the 28 kilometers traveled by the geologists on the third day. Knowing that 28 kilometers is
of the path is the 28 kilometers traveled by the geologists on the third day. Knowing that 28 kilometers is ![]() of the total path, we can find the length of the path through the valley:
of the total path, we can find the length of the path through the valley:
28 : 4 × 9 = 7 × 9 = 63 km
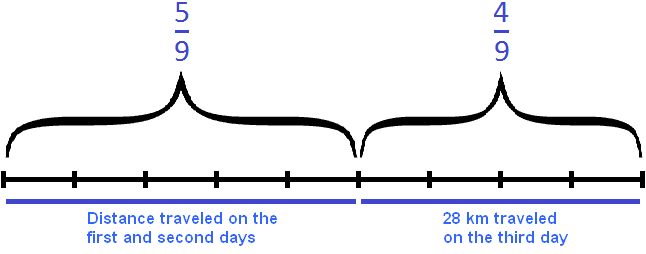
Check
63 : 9 × 5 = 7 × 5 = 35
63 : 9 × 4 = 7 × 4 = 28
35 + 28 = 63
63 = 63
Task 20. The mass of a can full of milk is 34 kg. The mass of a half-filled can is 17.75 kg. What is the mass of the empty can?
Solution
Let's subtract the mass of the can filled with milk from the mass of the half-filled can. Thus, we get the mass of the contents of the half-filled can, but without taking into account the mass of the can:
34 kg - 17.75 kg = 16.25 kg.
16,25 is the mass of the contents of the can half-full. Multiply this mass by 2, and you get the mass of the full can:
16.25 kg × 2 = 32.5 kg
32.5 kg is the mass of the can's contents. To calculate the mass of an empty can, subtract the mass of its contents from 34 kg, i.e. 32.5 kg
34 kg - 32,5 kg = 1,5 kg
Answer: the mass of the empty can is 1.5 kg.
Task 21. Cream is 0.1 mass of milk and butter is 0.3 mass of cream. How much butter can be obtained from the daily milk yield of a cow equal to 15 kg of milk?
Solution
Determine how many kilograms of cream can be obtained from 15 kg of milk. To do this, find 0.1 part of 15 kg.
15 × 0.1 = 1.5 (kg of cream)
Now determine how much butter you can get from 1.5 kg of cream. To do this we find 0.3 part of 1.5 kg
1.5 kg × 0.3 = 0.45 (kg of butter).
Answer: you can get 0.45 kg of butter from 15 kg of milk.
Task 22. 100 kg of linoleum glue contains 55 kg of asphalt, 15 kg of rosin, 5 kg of varnish and 25 kg of gasoline. How much of this glue is made up of each of its constituents?
Solution
Let's imagine that 100 kg of glue is like 100 parts. Then 55 parts are asphalt, 15 parts are rosin, 5 parts are olive, and 25 parts are gasoline. Write down these parts as fractions, and if possible, reduce the resulting fractions:
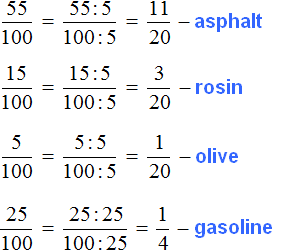
Answer: ![]() of the glue is asphalt,
of the glue is asphalt, ![]() is rosin,
is rosin, ![]() is olive,
is olive, ![]() is gasoline.
is gasoline.
Exercises
solution
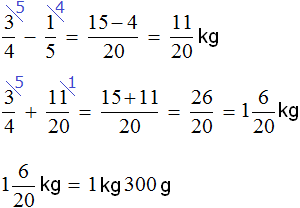
Answer: the weight of the two bags together is 1 kg 300 g
solution
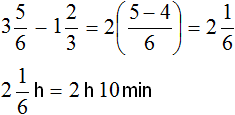
Second method
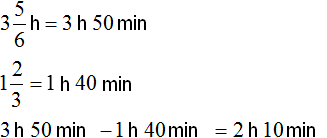
Answer: movie lasted 2 hours and 10 minutes.
solution
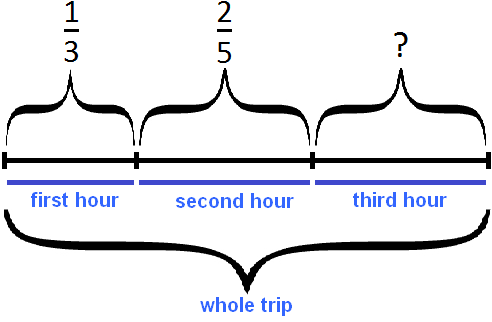
Determine the part of the path traveled by the skier for two hours of movement. To do this, add the fractions expressing the paths traveled during the first and second hours:
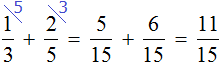
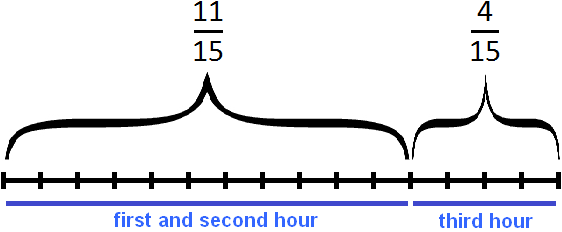
Determine the part of the distance traveled by the skier during the third hour. To do this, subtract from all parts the part of the path traveled during the first and second hours of movement:
![]()
Answer: in the third hour the skier went 4/15 of the total distance.
solution
Let's identify some of the students who participated in soccer, basketball, and jumping:
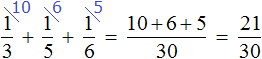
Let's identify some of the students who participated in the run:
![]()
Let's find out how many more (or fewer) runners than soccer players there are. First, let's compare fractions ![]() and
and ![]()
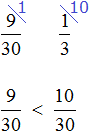
We needed to find out by what fraction there are more (or fewer) runners than soccer players. We found out that there are fewer runners than soccer players. Let's find out by what fraction there are fewer of them:
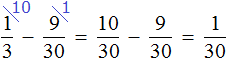
There are fewer runners than soccer players by 1/30th.
Now let's find out by how many more (or fewer) runners than basketball players. First, let's compare the fractions 9/30 and 1/5
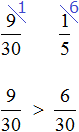
We needed to find out how many more (or less) runners than basketball players. We found out that there are more runners than basketball players. Let's find out how many more of them there are:
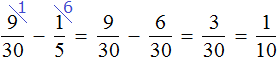
Runners outnumber basketball players by 1/10th.
Answer: runners were 1/30th less than soccer players and 1/10th more than basketball players.
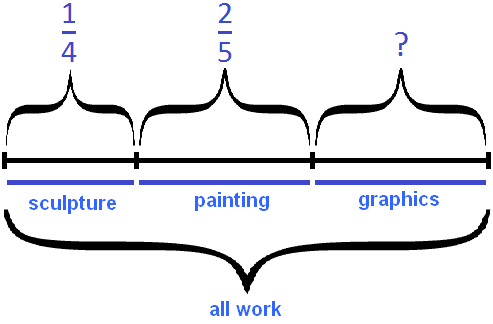
Task 5. There are paintings, sculptures, and graphics in an exhibition of artwork. Sculpture makes up ![]() of all the works, painting makes up
of all the works, painting makes up ![]() , and graphics makes up the rest. What part of all the works is graphic art?
, and graphics makes up the rest. What part of all the works is graphic art?
solution
Add fractions expressing sculpture and painting:
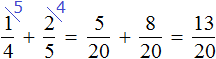
Let's determine what part of all the work is graphics:
![]()
Answer: 7/20 of all work is painting.
Task 6. Workers repaired a road that was 820 m long over three days. On Tuesday they repaired ![]() of that road, and on Wednesday they repaired
of that road, and on Wednesday they repaired ![]() of the rest. How many meters of the road were repaired by the workers on Thursday?
of the rest. How many meters of the road were repaired by the workers on Thursday?
solution
Determine the length of the road repaired on Tuesday:
820 : 5 × 2 = 328 m
Determine the length of the road repaired on Wednesday. It is known that on that day, workers repaired 2/3 of the remaining road. The remaining road is 820-328, that is 492
492 : 3 × 2 = 328 m
Determine the length of the road repaired on Thursday. To do this, subtract from 820 the length of the roads repaired on Tuesday and Wednesday:
820 − (328 + 328) = 820 − 656 = 164 m
Answer: On Thursday, workers repaired 164 meters of road.
Task 7. There are three stories in the book. The girl read the first story in ![]() h, it took her
h, it took her ![]() h longer to read the second story, and it took her
h longer to read the second story, and it took her ![]() h less to read the third story than it took her to read the first and the second stories together. How long did it take the girl to read the whole book?
h less to read the third story than it took her to read the first and the second stories together. How long did it take the girl to read the whole book?
solution
Determine the time it took the girl to read the first story. She read it in a third of an hour. A third of an hour is 20 minutes.
60 : 3 × 1 = 20 min
Determine the time it took the girl to read the second story. She read it for 1/6 hour longer. One-sixth of an hour is 10 minutes. Add 10 minutes to 20 minutes to get the time of reading the second story:
20 + 10 = 30 min
Determine the time it took the girl to read the third story. She read it 7/12 hours less than reading the first and second stories together. 7/12 h is 35 minutes. Subtract 35 from the time spent reading the first and second story together (50 min).
50 − 35 = 15 m
Determine how long it took the girl to read the whole book:
20 + 30 + 15 = 65 min = 1 h 5 min
It took the girl 1 hour and 5 minutes to read the whole book. Let's solve this problem with fractions. This way it can be shortened considerably:
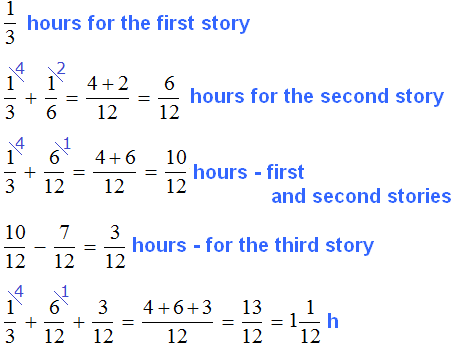
![]() is one whole hour and 1/12 of an hour, and one twelfth of an hour is 5 minutes.
is one whole hour and 1/12 of an hour, and one twelfth of an hour is 5 minutes.
Answer: it took the girl ![]() of an hour to read the whole book
of an hour to read the whole book
Task 8. One ton of raw cotton can be used to produce 3,400 meters of fabric, 1.05 tons of edible oil, and 0.225 tons of cake. How many meters of cloth, edible oil and cake can be produced from 32.4 quintals of raw cotton?
solution
Let's convert 32.4 quintals to tons. One ton is 10 quintals. To find out how many of these ten quintals (meaning tons) are in 32.4 quintals, divide 32.4 by 10
32,4 : 10 = 3,24 t
Determine how many meters of fabric can be obtained from 3.24 tons of raw cotton. One ton, as stated in the problem, yields 3,400 meters of fabric. And 3.24 tons will yield 3.24 times more fabric
3400 × 3,24 = 11016 meters of fabric.
Determine how much edible oil can be obtained from 3.24 tons of raw cotton. One ton, as stated in the problem, yields 1.05 tons of edible oil. And 3.24 tons will yield 3.24 times as much oil
1,05 × 3,24 = 3,402 quintal of edible oil
Determine how much cake can be obtained from 3.24 tons of raw cotton. One ton, as stated in the problem, yields 0.225 tons of cake. And 3.24 tons will yield 3.24 times as much cake
0,225 × 3,24 = 0,729 tons of cake
Answer: From 32.4 quintals of raw cotton you can get 11016 meters of fabric, 3.402 quintals of edible oil and 0.729 tons of cake.
solution
Knowing that 0.2 of the whole path is 12 km, we can find the whole path. To find an unknown number by a decimal fraction, divide the known number by the decimal fraction
12 : 0.2 = 60 km
Answer: The tourists walked 60 km.
solution
Knowing that 0.7 of the book is 56 pages, we can find out how many total pages are in the book. To find an unknown number by a decimal, divide the known number by the decimal
56 : 0.7 = 80 (pages total)
Let's see how much left to read
80 - 56 = 24 (pages left to read)
Answer: There are 80 pages in the book. There are 24 more pages to read.
solution
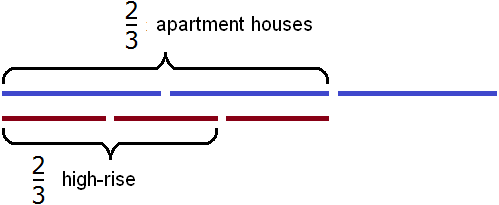
Let's divide 2/3 residential houses into three parts:
![]()
Now one-third of the high-rise buildings account for 2/9 of all buildings. Originally, all buildings were divided into three equal parts. Now they are divided into nine equal parts. Residential buildings, which were previously expressed as a fraction of 2/3, are now expressed as a fraction of 6/9
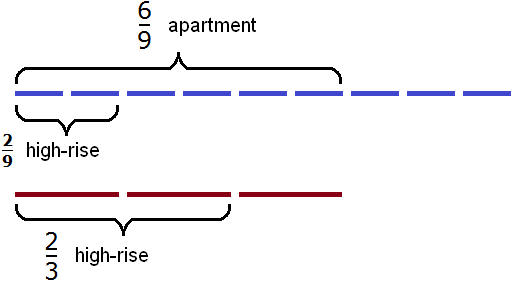
To find out how many high-rise buildings there are in two-thirds, multiply 2/9 by 2
![]()
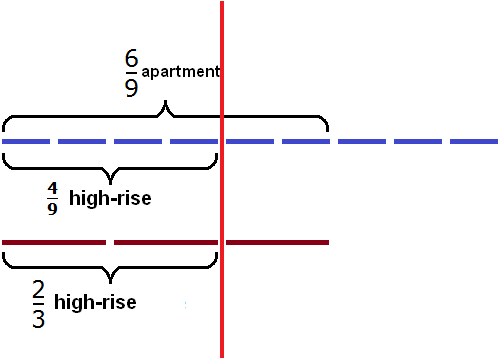
Answer: residential high-rise buildings make up 4/9 of all buildings in the city.
solution
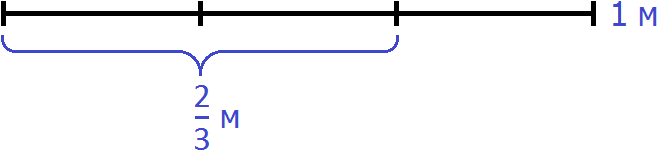
Let's diagram one meter of rope:
![]()
Let's highlight 2/3 of a meter in this figure:
Here we also allocate 1/2 meter
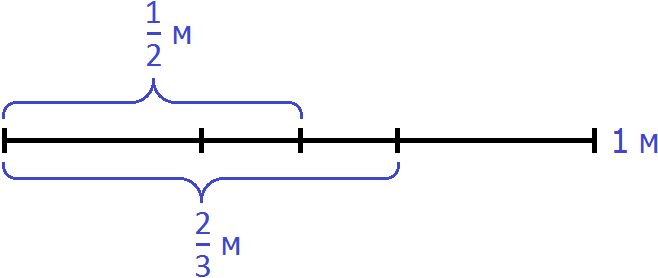
There is one piece left unselected for 2/3 m. Let's find out what kind of piece it is. To do this subtract 1/2 from 2/3
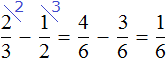
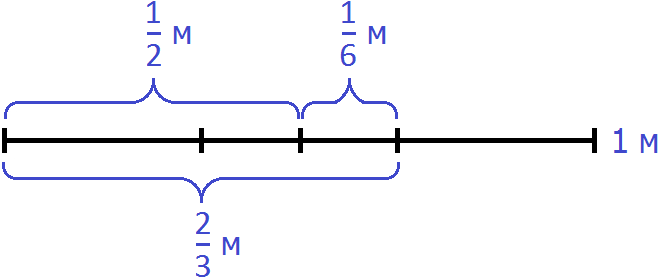
1/6 m is the part of the rope to be cut. Then we get 1/2 m of rope.
Now it remains to find out how many times 2/3 m contains 1/6 m
![]()
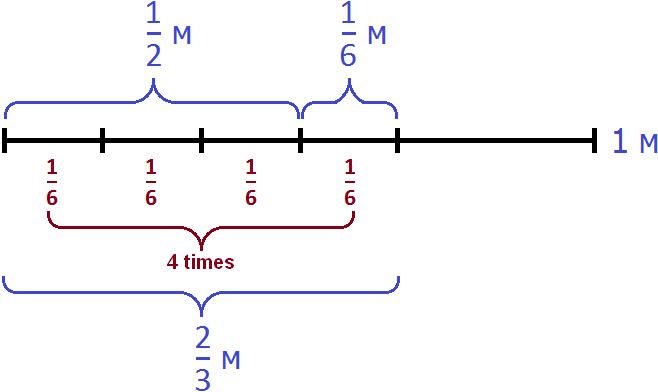
So, in order to cut off 1/2 m of rope from 2/3 m without measuring, you have to fold the rope in four and cut off one part. The remainder is half of one meter.
Answer: In order to cut 1/2 m from a rope that is 2/3 m long, you must fold the rope in four and cut off one part of it. The remaining part will become 1/2 m of rope.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.