In this lesson we will look at concepts such as divisors and multiples.
What is a divisor?
We know that the divisor is a number by which another number is to be divided.
For example, in the expression 8 : 2 = 4, the divisor is number 2. This number shows how many parts we need to divide number 8. After dividing it, the answer is 4. As you can see from the example, the number 8 is divisible by the number 2 without a remainder. The number 2 is said to be the divisor of number 8.
Example 1. The number 2 is a divisor of 8 because 8 is divisible by 2 without a remainder:
8 : 2 = 4
Example 2. The number 3 is a divisor of 9 because 9 is divisible by 3 without a remainder:
9 : 3 = 3
Example 3. The number 4 is not a divisor of 10 because 10 is not divisible by 4 without a remainder:
10 : 4 = 2 (2 in the remainder)
Definition. The divisor of a is the number by which a is divisible without a remainder.
This definition contains the variable a. Substitute any number instead of this variable, for example number 12, and read the definition:
The divisor of 12 is the number by which 12 is divided without a remainder.
Let's try to list these numbers:
1, 2, 3, 4, 6, 12
All of these numbers are divisors of number 12 because number 12 is divisible by them without a remainder. Let's show this:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Multiples
Definition. If any number is divisible by another number without a remainder, it is a multiple of that number.
For example, 6 without a remainder is divisible by 3. Therefore, 6 is a multiple of 3.
6 : 3 = 2
Definition. A multiple of a is a number that is divisible without a remainder by a.
This definition contains the variable a. Substitute any number instead of this variable, for example number 5, and read the definition:
A multiple of 5 is a number that is divisible without a remainder by 5.
Any number has infinitely many multiples. For example, the first multiples of 5 are 5, 10, 15, 20, 25. All of them are multiples of 5 because they are divisible by 5 without a remainder:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Divisibility Signs
Definition. Divisibility signs are used to speed up the process of dividing numbers. There are many signs of divisibility and some interesting algorithms that greatly speed up the solution and free you from unnecessary calculations. Consider the most popular of them.
Divisibility signs by 10
Any number that ends in zero is divisible by 10 without a remainder. To get the quotient, it is enough to discard the number 0 in the divisor.
For example, 380 : 10 = 38. We have simply discarded the last zero in 380.
If we have an expression of this form, 385 : 10, we get 38 and a 5 in the remainder, because 380 : 10 = 38, and a 5 is the remainder that is not divided.
Thus, if the number ends in 0, then it is divided by 10 without a remainder. If it ends in another digit, then it is not divisible by 10 without a remainder. The remainder in this case is equal to the last digit of the number. Indeed, in the example 385 : 10 = 38 (5 in the remainder), the remainder equals the last digit in the number 385, that is, a five.
Divisibility signs by 5 and by 2
Any number that ends in zero is divisible without a remainder by both 5 and 2.
Examples:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Divisibility signs by 5
If a number ends in 0 or 5, it is divided by 5 without a remainder.
Examples:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Divisibility signs by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example, consider number 27, the sum of its digits is 2 + 7 = 9. Nine, as we know, is divisible by 3, so 27 is also divisible by 3:
27 : 3 = 9
The sign of divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
For example, consider the number 18. The sum of its digits is 1 + 8 = 9. Nine is divisible by nine, so 18 is divisible by 9.
18 : 9 = 2
Consider the number 846. The sum of its digits is 8 + 4 + 6 = 18. Eighteen is divisible by nine, so 846 is divisible by 9:
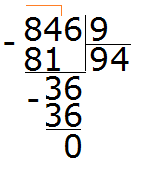
Even and odd numbers
Definition. An even number is a number that is divisible by 2 without a remainder.
For example, 20 is an even number because it is divisible by 2 without a remainder:
20 : 2 = 10
Definition. An odd number is an odd number if it is divided by 2 and leaves a remainder of 1.
For example, 21 is odd because it is divided by 2 and leaves a remainder of 1:
21 : 2 = 10 (1 in the remainder)
How can you tell an even number from an odd number without having to divide by 2? Very simple. Even numbers are 0, 2, 4, 6, 8, and odd numbers are 1, 3, 5, 7, 9. If the number ends in an even number, then it is an even number. If the number ends in an odd number, then it is an odd number.
For example, the number 308 is even because it ends in an even number. The number 1024 is also even because it ends in an even number.
And the numbers 305 and 1027 are odd because they end in odd digits.
Prime and composite numbers
Definition. A prime is a number that is divisible by itself and 1 without a remainder. In other words, it has only two divisors.
For example, number 5 is divisible by itself and one without a remainder:
5 : 1 = 5
5 : 5 = 1
So the number 5 is a prime number.
Definition. A composite number is a positive integer greater than 1 that has divisors other than 1 and itself.
For example, number 4 is a composite number because it has two or more divisors: 4, 2, and 1.
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
So the number 4 is a composite number.
Factorization of a composite number into prime factors
Any composite number can be factorized into prime factors. We did something similar in the lesson on substitution in expressions. In this lesson we learned that any number in an expression can be replaced by the same number but written in a different form.
For example, the number 6 can be written as the sum of 4 + 2 or as the quotient 12 : 2 or as the product 2 × 3. The last entry 2 × 3 can be called a decomposition of the number 6 into prime factors.
The essence of the decomposition of a number into prime factors is to represent this number as a product of several prime factors.
Let's decompose the number 4 into prime factors. To do this, we gather this number from other numbers, and write them with the multiplication sign (×). The number 4 is composed of the numbers 2 and 2. These two numbers are simple multipliers that make up the number 4
4 = 2 × 2
Decompose the number 6 into factors. The number 6 can be assembled from the numbers 2 and 3. These two numbers are the simple multipliers that make up number 6
6 = 2 × 3
Decompose the number 8 into factors. This number can be decomposed into factors 2 and 4, and the factor 4 can be decomposed into two factors: 2 and 2. So we write its decomposition instead of the four:
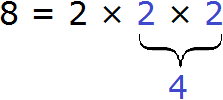
Large numbers are decomposed in the same way. First they are decomposed into large multipliers, then these large multipliers are decomposed into small multipliers. And so on until each multiplier becomes a prime number.
For example, let's decompose the number 180 into prime factors. The number 180 is two multipliers 18 and 10
180 = 18 × 10
Now decompose the multipliers 18 and 10 into other multipliers:
18 = 3 × 6
10 = 5 × 2
Now decompose the highlighted blue six. This is the last large multiplier that can be decomposed into prime multipliers:
6 = 2 × 3
Now put all the simple multipliers together:

Only a composite number can be decomposed into multipliers. A prime number cannot be decomposed into multipliers. That is why when the decomposition reaches prime numbers, we do not decompose the prime numbers further.
There is a second method of decomposition into prime factors. It is simpler and better suited for large numbers. The essence of this method is that first draw a vertical line. Then to the left of this line are written divisors, and to the right - divisors, which are later collected into multipliers.
When decomposing a number by this method, the signs of divisibility are used, such as: the signs of divisibility by 2, by 3, by 5 and others.
For example, decompose the previous number 180 this way.
Draw a vertical line and on the left side write the first divisor of 180

Now we apply the signs of divisibility. First, we check if 180 is divisible by 2. If it is divisible, you should write this two to the right of the vertical line.
180 is divisible by 2 because 180 ends in zero. Write the two to the right of the vertical line:
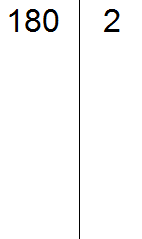
Now divide 180 by 2 and get the second divisor 90. Write this divisor to the left of the vertical line:
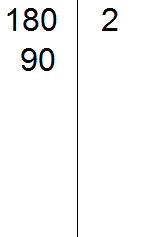
Now divide by 90. Again we apply the signs of divisibility. We check if 90 is divisible by 2.
90 is divisible by 2 because 90 ends in zero. Write the two to the right of the vertical line:
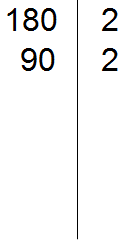
Now divide 90 by 2 to get the third divisor 45. Write this divisor to the left of the vertical line:
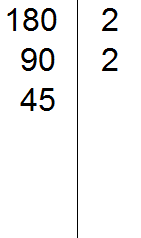
Now divide by 45. Again we apply the signs of divisibility. Check if 45 is divisible by 2.
45 is not divisible by 2. Then we check if 45 is divisible by 3.
45 is divisible by 3, because the sum of digits 4 and 5 is divisible by 3. Write the 3 to the right of the vertical line:
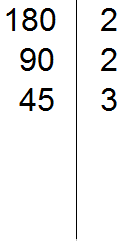
We divide 45 by 3 to get the fourth divisor 15. Write this divisor to the left of the vertical line:
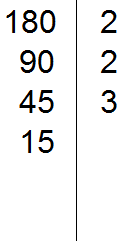
Now divide 15. We check if 15 is divisible by 2.
15 is not divisible by 2. Then we check if 15 is divisible by 3.
15 is divisible by 3, because the sum of digits 1 and 5 is divisible by 3. Write the 3 to the right of the vertical line:

We divide 15 by 3, so we get the fifth divisor 5. Write the five to the left of the vertical line:
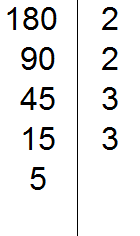
Now divide 5. We check if 5 is divisible by 2.
5 is not divisible by 2. Then we check if 5 is divisible by 3.
5 is not divisible by 3. Then we check if 5 is divisible by 5.
5 is divisible by 5. Write this 5 to the right of the vertical line:
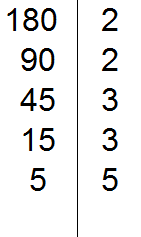
We divide 5 by 5 and get the sixth divisor 1. Write this one to the left of the vertical line:
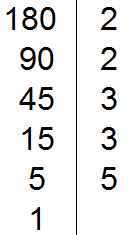
This completes the division, since we have reached one. The divisors that are written to the right of the vertical line must be prime numbers. So when the divisor 5 did not divide by 2 and then did not divide by 3, we tried to divide it by 5 without trying to divide by 4 because 4 is not a prime but a composite number.
Now we write down in one row all the divisors that are written to the right of the vertical line. They will be the decomposition of number 180 into prime factors. It is desirable to write them down, starting with the smallest. This allows you to order them in ascending order:

Don't be upset if you have trouble decomposing numbers into prime factors. This topic requires a little practice. For practice you can decompose the following numbers into prime factors: 256, 378, 512.
Finding divisors of a number
At the beginning of this lesson it was said that a divisor is a number by which another number is divisible without a remainder.
For example, number 2 is the divisor of number 6 because number 6 can be divided by 2 without a remainder
6 : 2 = 3
Another divisor of number 6 is number 3
6 : 3 = 2
Another divisor of number 6 is number 1
6 : 1 = 6
Finally, the divisor of number 6 is the number itself
6 : 6 = 1
List all the divisors of number 6
1, 2, 3, 6
Sometimes you need to find all the divisors of a number. To understand how to do this, let's look at some examples.
Example 1. Find the divisors of number 12
First, one is a divisor of any number. Let us also have the first divisor of 12 be 1.
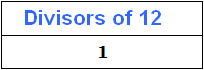
Now decompose the number 12 into prime factors:

We obtained the decomposition 2 × 2 × 3.
In the process of decomposition of number 12 into prime factors, we divided it into numbers 2 and 3. They divided number 12 without a remainder, so they are also divisors of number 12. Let's add these two numbers to our table of divisors:

To get the remaining divisors of number 12, you need to find all possible products of its prime factors among themselves. The resulting answers will be the remaining divisors of number 12.
We have decomposed number 12 into prime factors 2 × 2 × 3. Find all possible products of these prime factors among themselves. The first product is 2 × 2. This product is equal to 4
2 × 2 = 4
Let's put number 4 in our table of divisors

The next possible product of prime factors of number 12 is the product of 2 × 3. This product is 6. Let's put the number 6 in our table of divisors:
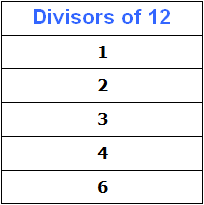
The last possible product of prime factors of number 12 is the product of all its factors, namely 2 × 2 × 3. This product is 12. Let's put the number 12 in our table of divisors:
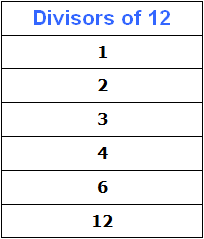
Thus, the divisors of number 12 are 1, 2, 3, 4, 6, 12.
Based on this example, we can form a rule for finding the divisors of a number:
To find the divisors of a number, you need to:
- write 1 as the first divisor;
- Decompose the original number into prime factors and write out of the resulting prime factors that are divisors of the original number (if a factor repeats, then write it out only once);
- find all possible products of obtained prime factors among themselves. The resulting answers will be the remaining divisors of the original number.
Example 2. Find the divisors of number 6
Write one as the first divisor of number 6:
1
Now decompose the number 6 into prime factors:
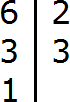
Write out from the resulting expansion those multipliers that are divisors of number 6. We see that these are multipliers 2 and 3. They will be the next divisors of number 6. Let's add them to our divisors:
1, 2, 3
Now find all possible products of prime factors of number 6. In this case, there is only one product, namely 2 × 3. This product is 6. Add 6 to our divisors:
1, 2, 3, 6
Thus, the divisors of number 6 are the numbers 1, 2, 3, 6.
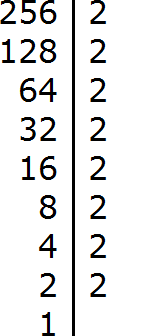
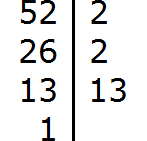
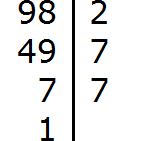
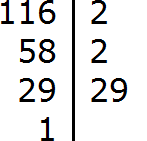
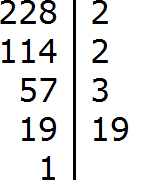
Comments
You are absolutely right, thank you for pointing that out, it has been corrected!
"A composite number is a number which is divisible by two or more numbers."
Isn't a number that is divisible only by two numbers a prime number?
I think you may have to correct this.
Prime numbers are those numbers that are divisible by themselves and by one (for example: 2, 3, 5, 7, etc.). Those numbers that are not only divided by themselves and by one, have more than two divisors are called composite numbers.
Hi, Erica. The divisor (2) is the number to the right of the division sign, the number by which we divide the dividend (5).
In this example and in any other, if the number is to the right of the division sign, that number is the Divisor (always!)
This page defines a divisor as a number that another number can be divided by without a remainder. Is that the only use of the word? I'm confused because when the Basic Operations page listed the different terminology for addition, subtraction, multiplication and division, I thought they were valid whether or not we were talking about whole numbers (as in, summands are called summands regardless of what numbers they represent).
So, in this example: 5 / 2 = 2.5 (where 5 is the dividend and 2.5 the quotient), is 2 still called the divisor (when 2 isn't a divisor of 5)?