Several rules apply to multiplication and division of integers. In this lesson we will look at each of them.
When multiplying and dividing integers, pay attention to the signs of the numbers. These will determine which rule to apply. Several multiplication and division laws should also be studied. Studying these rules will help avoid some unfortunate mistakes in the future.
Laws of Multiplication
We looked at some of the laws of mathematics in the lesson Laws of Mathematics. But we didn't look at all of the laws. There are many laws in mathematics and it makes more sense to study them sequentially as needed.
First, let's remember what multiplication consists of. Multiplication consists of two parameters: a multiplicand, a multiplier, and a product. For example, in the expression 3 × 2 = 6, number 3 is the multiplicand, number 2 is the multiplier, number 6 is the product.

The multiplicand shows exactly what we are incrementing. In our example we are incrementing number 3.
The multiplier shows how many times the multiplicand should be increased. In our example, the multiplier is number 2. This multiplier shows how many times multiplier 3 should be increased. That is, in the multiplication operation the number 3 will be doubled.
The product is actually the result of the multiplication operation. In our example, the product is the number 6. This product is the result of multiplying 3 by 2.
The expression 3 × 2 can also be understood as the sum of two threes (3+3). The multiplier 2 in this case will show how many times to repeat number 3:
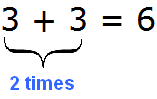
Thus, if you repeat the number 3 twice in a row, you get the number 6.
Commutative law of multiplication
A multiplicand and a multiplier are referred to by one common word - the factors. The commutative law of multiplication is as follows:
We can swap multiplicand and multiplier over and still get the same product (result).
Let's check if this is true. Let's multiply 3 by 5, for example. Here 3 and 5 are the factors.
3 × 5 = 15
Now swap the factors:
5 × 3 = 15
In both cases we get the answer 15, so we can put an equal sign between the expressions 3 × 5 and 5 × 3 because they are equal to the same value:
3 × 5 = 5 × 3
15 = 15
And with the help of variables, the commutative law of multiplication can be written as follows:
a × b = b × a
where a and b are the factors
Associative Law of Multiplication
When multiplying it doesn't matter how we swap and group the numbers.
For example, an expression 3 × 2 × 4 consists of several factors. To calculate it, you can multiply 3 and 2, then multiply the product obtained by the remaining number 4. It would look like this:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
This was the first version of the solution.
The second option is to multiply 2 and 4, then multiply the product obtained by the remaining number 3. It would look like this:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
In both cases we get the answer 24. Therefore, we can put an equal sign between the expressions (3 × 2) × 4 and 3 × (2 × 4) because they are equal to the same value:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
and using a,b,c,
the associative law of multiplication can be written as follows:
a × b × c = (a × b) × c = a × (b × c)
where a, b, c can be any number.
The distributive law of multiplication
multiplying a number by a group of numbers added together is the same as doing each multiplication separately.
For example, find the value of the expression (2 + 3) × 5
The expression in parentheses is a sum. This sum must be multiplied by the number 5. To do this, each summand of this sum, that is, the numbers 2 and 3 must be multiplied by the number 5, and then the results must be added:
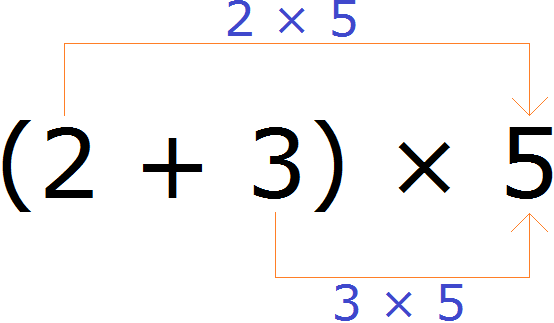
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
So the value of the expression (2 + 3) × 5 is 25.
Using variables, the distributive law of multiplication is written as follows:
(a + b) × c = a × c + b × c
where a, b, c can be any number.
The Multiplication Property of Zero
This law says that if there is at least one zero in any multiplication, the answer will be zero.
A product is zero if at least one of the factors is zero.
For example, the expression 0 × 2 is zero
0 × 2 = 0
In this case, the number 2 is a multiplier and shows how many times to increase the multiplicand. That is, how many times to increase zero. Literally, this expression reads like this: "to increase zero by a factor of two". But how can you double zero if it is zero?
In other words, if "nothing" is doubled, or even a million times, you still get "nothing".
And if we swap the factors in the expression 0 × 2, we get zero again. This we know from the previous permutation law:
0 × 2 = 2 × 0
0 = 0
Usage of the law of multiplication by zero:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
In the last two examples there are several factors. When we saw zero in them, we immediately put zero in the answer, applying the law of multiplication by zero.
We have looked at the basic laws of multiplication. Now let's look at the multiplication of integers itself.
Multiplication of integers
Example 1. Find the value of the expression -5 × 2
This is a multiplication of numbers with different signs. -5 is a negative number and 2 is a positive number. The following rule should be applied for such cases:
When you multiply two integers with different signs, the result is always negative.
−5 × 2 = − (5 × 2) = − (10) = −10
Usually written shorter: −5 × 2 = −10
Any multiplication can be represented as a sum of numbers. For example, consider the expression 2 × 3. It equals 6.
2 × 3 = 6
The multiplier in this expression is the number 3. This multiplier shows how many times the two should be increased. But the expression 2 × 3 can also be understood as the sum of three twos:
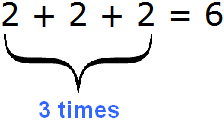
The same happens with the expression -5 × 2. This expression can be represented as the sum of
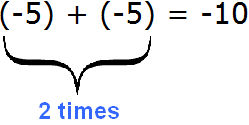
And the expression (-5) + (-5) equals -10. We know this from the last lesson. This is the addition of negative numbers. Recall that the result of adding negative numbers is a negative number.
Example 2. Find the value of the expression 12 × (-5)
This is a multiplication of numbers with different signs. 12 is a positive number, (-5) is a negative number.
Again we apply the previous rule. When you multiply two integers with different signs, the result is always negative:
12 × (−5) = − (12 × 5) = − (60) = −60
Usually the solution is written in a shorter form:
12 × (−5) = −60
Example 3. Find the value of the expression 10 × (-4) × 2
This expression consists of several factors. First, multiply 10 and (-4), then multiply that number by 2. At the same time we will apply the rules we learned earlier:
First act:
10 × (−4) = −(10 × 4) = (−40) = −40
Second act:
−40 × 2 = −(40 × 2) = −(80) = −80
So the value of the expression 10 × (-4) × 2 is -80
Let's write down the solution shorter:
10 × (−4) × 2 = −40 × 2 = −80
Example 4. Find the value of the expression (-4) × (-2)
This is the multiplication of negative numbers. In such cases the following rule should be applied:
When you multiply two negative numbers (with the same signs), the result is always positive
(−4) × (−2) = 8
We traditionally do not write down the plus, so we just write down the answer 8.
Let's write down a shorter solution (-4) × (-2) = 8
The question arises why the multiplication of negative numbers suddenly results in a positive number. Let's try to prove that (-4) × (-2) equals 8 and nothing else.
Let us first write the following expression:
4 × (−2)
Let's put it in parentheses:
( 4 × (−2) )
Add to this expression our expression (-4) × (-2). We also put it in parentheses:
( 4 × (−2) ) + ( (−4) × (−2) )
Let's equate all this to zero:
(4 × (−2)) + ((−4) × (−2)) = 0
Now begins the most interesting part. The point is that we have to calculate the left part of this expression, and the result is 0.
So, the first product (4 × (-2)) is -8. Write the number -8 in our expression instead of the product (4 × (-2))
−8 + ((−4) × (−2)) = 0
Now, instead of the second work, temporarily put a dotted line
−8 + … = 0
Now look carefully at the expression -8 + ... = 0. What number should be in place of the ellipsis for the equality to hold? The answer is obvious. Instead of the "...
" there should be a positive number 8 and no other number. This is the only way to keep the equality. Because -8 + 8 equals 0.
Return to the expression -8 + ((-4) × (-2)) = 0 and instead of the product ((-4) × (-2)) write the number 8
−8 + 8 = 0
Example 5. Find the value of -2 × (6 + 4)
Apply the distributive law of multiplication, that is, multiply -2 by each summand of (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Now let's perform multiplication and add up the results. At the same time we will apply the previously studied rules. You can skip the entry with modules in order not to clutter the expression
First action:
−2 × 6 = −12
Second action:
−2 × 4 = −8
Third action:
−12 + (−8) = −20
So the value of the expression -2 × (6 + 4) is -20
Let us write down the solution shorter:
−2 × (6 + 4) = (−12) + (−8) = −20
Example 6: Find the value of (-2) × (-3) × (-4)
The expression consists of several factors. First, multiply -2 and -3, and multiply the product obtained by the remaining number -4. Let us skip the modulo notation so as not to overload the expression
First action:
(−2) × (−3) = 6
Second action:
6 × (−4) = −(6 × 4) = −24
Then the value of the expression (-2) × (-3) × (-4) is -24
Let's write down the solution shorter:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Laws of division
Before you can divide integers, you must learn the two laws of division.
First of all, let's remember what division consists of. Division consists of three parameters: the dividend, the divisor, and the quotient.
For example, in the expression 8 : 2 = 4, 8 is the dividend, 2 is the divisor, and 4 is the quotient.

The dividend shows exactly what we are dividing. In this example, we are dividing number 8.
The divisor is a number by which another number is to be divided. In this example, the divisor is the number 2. That is, during the division operation, the number 8 will be divided into two parts.
The quotient is actually the result of the division operation. In our example, the quotient is the number 4. This quotient is the result of dividing 8 by 2.
Next, consider the laws of division.
You can't divide by zero
It is forbidden to divide any number by zero.
The fact is that division is the inverse of multiplication. This phrase can be understood in the literal sense. For example, if 2 × 5 = 10, then 10 : 5 = 2.
You can see that the second expression is written in reverse order. If, for example, we have two apples and we want to increase them by a factor of five, we write 2 × 5 = 10. That would make ten apples. Then if we want to write the ten apples back down to two apples, we write 10 : 5 = 2.
We can do the same with other expressions. If, for example, 2 × 6 = 12, we can go back to the original number 2. To do this, just write the expression 2 × 6 = 12 in reverse order, dividing 12 by 6
12 : 6 = 2
Now consider the expression 5 × 0. We know from the laws of multiplication that a product is zero if at least one of the factors is zero. So the expression 5 × 0 equals zero
5 × 0 = 0
If we write this expression in reverse order, we get:
0 : 0 = 5
Immediately striking is the answer 5, which is the result of dividing zero by zero. This is impossible.
Another similar expression can be written in reverse order, e.g., 2 × 0 = 0
0 : 0 = 2
In the first case, dividing zero by zero we got 5, and in the second case we got 2.
That is, each time we divide zero by zero, we can get different values, and this is unacceptable.
The second explanation is that to divide the dividend by the divisor means to find such a number, which when multiplied by the divisor will give the dividend.
For example, the expression 8 : 2 means to find such a number which, when multiplied by 2, yields 8
… × 2 = 8
Here instead of dots there should be a number that, when multiplied by 2, will give the answer 8. To find this number, simply write the expression in reverse order:
8 : 2 = 4
We got the number 4. Write it instead of the "..." :
4 × 2 = 8
Now let's imagine that we need to find the value of the expression 5 : 0. In this case, 5 is the dividend and 0 is the divisor. To divide 5 by 0 means to find such a number which, when multiplied by 0, gives 5
… × 0 = 5
Here, instead of a "...", there should be a number that, when multiplied by 0, gives the answer 5. But there is no number that, when multiplied by zero, gives 5.
The expression ... × 0 = 5 contradicts the law of multiplication by zero, which states that the product is zero when at least one of the factors is zero.
So it makes no sense to write down the expression ... × 0 = 5 in reverse order, dividing 5 by 0. That is why it is said that one cannot divide by zero.
Using variables, this law is written as follows:
![]() , at b ≠ 0
, at b ≠ 0
This expression can be read like this:
The number a can be divided by the number b, provided that b is not zero.
Quotient property
This law says that if the dividend and the divisor are multiplied or divided by the same number, the quotient will not change.
For example, consider the expression 12 : 4. The value of this expression is 3
12 : 4 = 3

Let's try to multiply the dividend and the divisor by the same number, for example number 4. If we believe the property of the quotient, we should again get number 3 in the answer
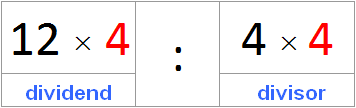
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Got an answer of 3.
Now let's try not to multiply, but to divide the divisor and the divisor by the number 4
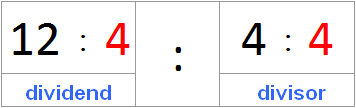
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Got an answer of 3.
We see that if the dividend and the divisor are multiplied or divided by the same number, the quotient does not change.
We have considered two laws of division. Next, let's look at division of integers.
Division of integers
Example 1. Find the value of the expression 12 : (-2)
This is dividing numbers with different signs. 12 is a positive number, (-2) is a negative number. To solve this example, divide the modulus of the dividend by the modulus of the divisor, and put minus in front of the answer.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Usually they write it down shorter:
12 : (−2) = −6
Example 2. Find the value of the expression -24 : 6
This is dividing numbers with different signs. -24 is a negative number, 6 is a positive number. Again, divide the modulus of the dividend by the modulus of the divisor, and put minus in front of the answer.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Let's write down the solution shortly:
−24 : 6 = −4
Example 3. Find the value of the expression -45 : (-5)
This is the division of negative numbers. To solve this example, divide the modulus of the dividend by the modulus of the divisor, and put a plus sign in front of the answer.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Let's write down the solution shortly:
−45 : (−5) = 9
Example 4. Find the value of the expression -36 : (-4) : (-3)
According to the order of operations, if the expression contains only multiplication or division, all actions must be performed from left to right in order.
Divide -36 by (-4), and divide the resulting number by -3
First act:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Second act:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Let's write down the solution shortly:
−36 : (−4) : (−3) = 9 : (−3) = −3
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.