Fractions can be added, subtracted, multiplied, and divided. Also, fractions can be compared to each other. Basically, everything you can do with regular numbers, you can do with fractions.
Adding fractions with common denominator
The addition of fractions:
- Addition with common denominators;
- Addition with different denominators.
First, let's learn how to add fractions with common denominators. This is simple.
To add fractions with the same denominators, add their numerators and leave the denominator unchanged.
For example, let's add fractions ![]() and
and ![]() . Add up the numerators and leave the denominator unchanged:
. Add up the numerators and leave the denominator unchanged:
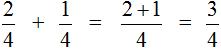
This example can be easily understood if you think of a pizza that is divided into four parts. If you add ![]() pizzas to
pizzas to ![]() pizza, you get
pizza, you get ![]() pizza:
pizza:
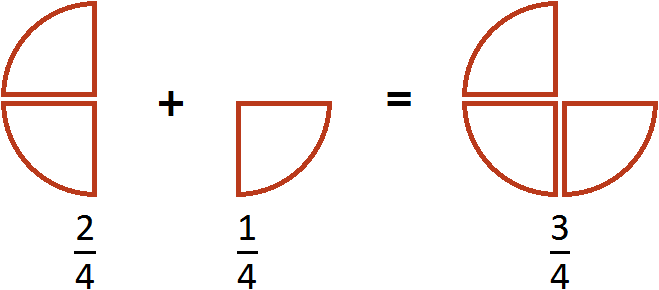
Example 2. Add fractions ![]() and
and ![]() .
.
Again we add the numerators and leave the denominator unchanged:
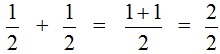
The answer is an improper fraction.![]() . If the end of the problem comes, it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part of it. In our case, the whole part is easy - two divided by two is one:
. If the end of the problem comes, it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part of it. In our case, the whole part is easy - two divided by two is one:
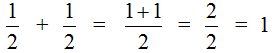
This example can be easily understood if you think of a pizza that is divided into two parts. If you add another ![]() pizza to the
pizza to the ![]() pizza, you get one whole pizza:
pizza, you get one whole pizza:
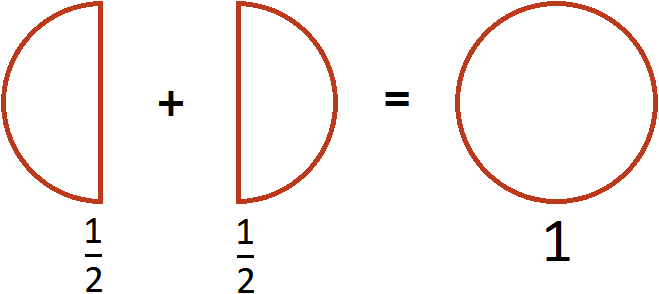
Example 3. Add fractions ![]() and
and ![]() .
.
Again we add the numerators and leave the denominator unchanged:
![]()
This example can be easily understood if you think of a pizza that is divided into three parts. If you add another ![]() pizza to
pizza to ![]() pizza, you get
pizza, you get ![]() pizza:
pizza:
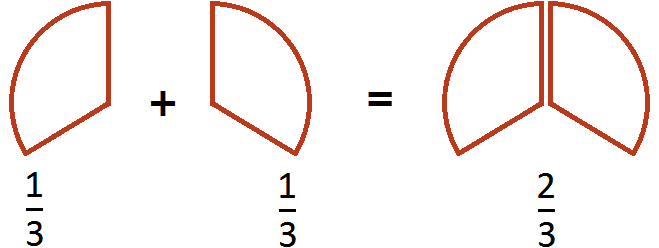
Example 4. Find the value of the expression 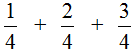
This example is solved in the same way as the previous ones. The numerators must be added and the denominator left unchanged:
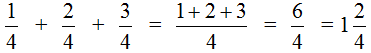
Let's try to represent our solution with a picture. If you add ![]() pizza to
pizza to ![]() pizza and add another
pizza and add another ![]() pizza, you get 1 whole pizza and another
pizza, you get 1 whole pizza and another ![]() pizza.
pizza.
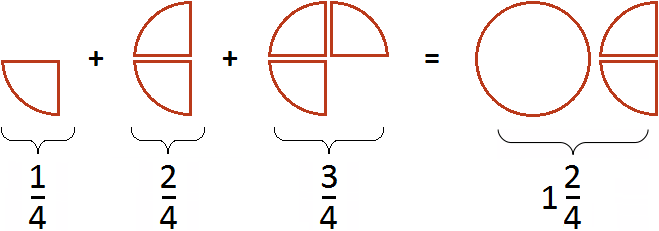
As you can see, there is nothing complicated about adding fractions with common denominators. It is enough to understand the following rules:
- To add fractions with the same denominators, add their numerators and leave the denominator unchanged;
- If the answer is an improper fraction, you need to select the whole part of it.
Adding fractions with different denominators
Now let's learn how to add fractions with different denominators. When fractions are added, the denominators of those fractions should be the same. But they are not always the same.
For example, fractions ![]() and
and ![]() can be added together because they have the same denominators.
can be added together because they have the same denominators.
But fractions ![]() and
and ![]() cannot be added together at once because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
cannot be added together at once because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
There are several ways to reduce fractions to the same denominator. Today we will look at just one of them, since the others may seem complicated to a beginner.
The essence of this method is that first we look for the least common multiple (LCM) of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional multiplier is obtained. Do the same with the second fraction - LCM divided by the denominator of the second fraction and get the second additional multiplier.
Then the numerators and denominators of the fractions are multiplied by their additional multipliers. As a result, fractions with different denominators are converted to fractions with the same denominators. And we already know how to add such fractions.
Example 1. Add fractions ![]() and
and ![]()
These fractions have different denominators, so you need to reduce them to the same (common) denominator.
First, find the least common multiple of the denominators of both fractions. The denominator of the first fraction is number 3, and the denominator of the second fraction is number 2. The least common multiple of these numbers is 6
LCM (2 and 3) = 6
Now back to fractions ![]() and
and ![]() . First, divide the LCM by the denominator of the first fraction and get the first additional multiplier. The LCM is 6, and the denominator of the first fraction is 3. Dividing 6 by 3, we get 2.
. First, divide the LCM by the denominator of the first fraction and get the first additional multiplier. The LCM is 6, and the denominator of the first fraction is 3. Dividing 6 by 3, we get 2.
The resulting number 2 is the first additional multiplier. Write it to the first fraction. To do this, make a small diagonal line above the fraction and write the additional multiplier found above it:
![]()
Do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is 6, and the denominator of the second fraction is 2. Dividing 6 by 2, we get 3.
The resulting number 3 is the second additional multiplier. Write it to the second fraction. Again make a small diagonal line over the second fraction and write the found additional multiplier over it:
![]()
Now we are all set for addition. It remains to multiply the numerators and denominators of the fractions by their additional multipliers:
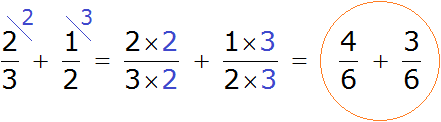
Look carefully at what we have come to. We came to the fact that fractions with different denominators turned into fractions with the same denominators. And we already know how to add such fractions. Let's solve this example to the end:
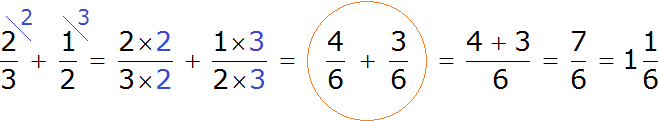
This completes the example. Add ![]() to
to ![]() and you get
and you get ![]() .
.
Let's try to represent our solution with a picture. If you add ![]() pizza to
pizza to ![]() pizza, you get one whole pizza and one sixth of a pizza:
pizza, you get one whole pizza and one sixth of a pizza:
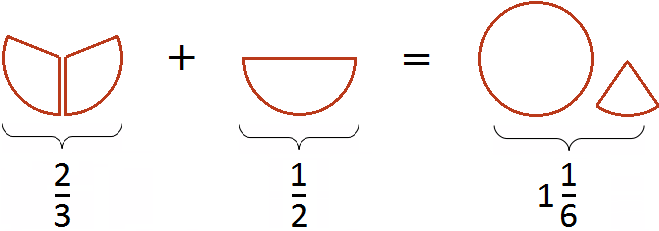
The reduction of the fraction to the same (common) denominator can also be shown. Bringing fractions ![]() and
and ![]() to a common denominator, we got fractions
to a common denominator, we got fractions ![]() and
and ![]() . The two fractions will be represented by the same pieces of pizza. The only difference will be that this time they will be divided into the same fractions (reduced to the same denominator).
. The two fractions will be represented by the same pieces of pizza. The only difference will be that this time they will be divided into the same fractions (reduced to the same denominator).
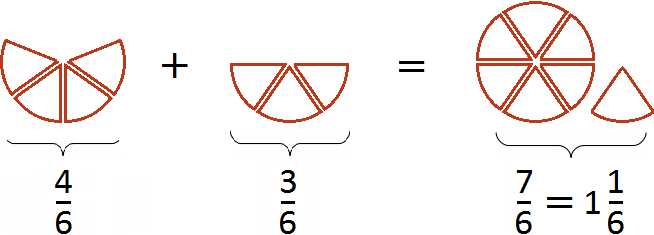
The first picture represents the fraction ![]() (four pieces of six), and the second picture represents the fraction
(four pieces of six), and the second picture represents the fraction ![]() (three pieces of six). Adding up these pieces we get
(three pieces of six). Adding up these pieces we get ![]() (seven pieces of six). This fraction is improper, so we highlighted the whole part of it. The result was
(seven pieces of six). This fraction is improper, so we highlighted the whole part of it. The result was ![]() (one whole pizza and another sixth of a pizza).
(one whole pizza and another sixth of a pizza).
Note that we have written this example in too much detail. In schools it is not customary to write in such a detailed way. You need to be able to quickly find the LCM of both denominators and additional multipliers to them, and quickly multiply the found additional multipliers by their numerators and denominators. If we were in school, we would have to write this example as follows:
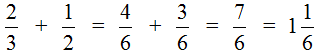
But there is also the other side of the coin. If you don't take detailed notes during the first stages of learning math, you start to get questions like "where did that number over there come from?", "why do fractions suddenly turn into completely different fractions?"
Therefore, at the first stages, it is advisable to write down every detail. You can brag only in the future, when the basics have been mastered.
To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:
- Find the LCM of the denominators of fractions;
- Divide the LCM by the denominator of each fraction and obtain an additional multiplier for each fraction;
- Multiply the numerators and denominators of fractions by their additional multipliers;
- Add fractions that have the same denominators;
- If the answer is an improper fraction, select the whole part of it;
Example 2. Find the value of the expression 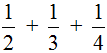 .
.
Let's use the instructions above.
Step 1. Find the LCM of the denominators of fractions
Find the LCM of the denominators of both fractions. The denominators of the fractions are numbers 2, 3, and 4.
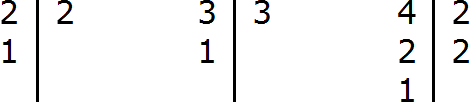
![]()
Step 2: Divide the LCM by the denominator of each fraction and obtain an additional multiplier for each fraction
Divide the LCM by the denominator of the first fraction. LCM is 12, and the denominator of the first fraction is 2. Divide 12 by 2 to get 6. We get the first additional factor 6. Write it over the first fraction:
![]()
Now divide the LCM by the denominator of the second fraction. LCM is 12, and the denominator of the second fraction is 3. We divide 12 by 3 and get 4. We have a second additional factor 4. Write it over the second fraction:
![]()
Now divide the LCM by the denominator of the third fraction. LCM is 12, and the denominator of the third fraction is 4. We divide 12 by 4 and get 3. We have a third additional factor of 3. Write it over the third fraction:
![]()
Step 3: Multiply the numerators and denominators of fractions by their additional multipliers
Multiply the numerators and denominators by their additional multipliers:
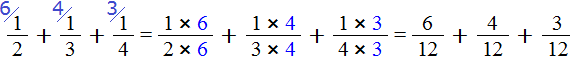
Step 4: Add fractions with the same denominators
We found that fractions with different denominators turned into fractions with the same (common) denominators. It remains to add these fractions. We add them up:
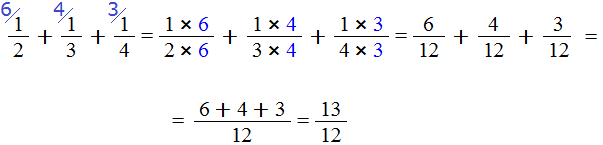
The addition did not fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is moved to the next line, and you must put an equal sign (=) at the end of the first line and at the beginning of the new line. The equality sign on the second line indicates that it is a continuation of the expression that was on the first line.
Step 5. If the answer is an Improper fraction, select the whole part of it
Our answer is an improper fraction. We must isolate the whole part of it. We do:
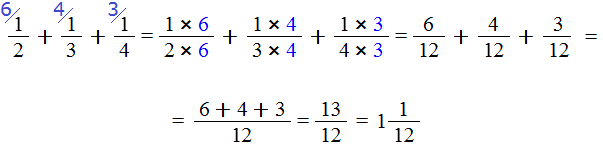
We got the answer ![]()
Subtracting fractions with common denominators
Subtraction of fractions is of two kinds:
- Subtracting fractions with common denominators
- Subtracting fractions with different denominators
First, we will learn how to subtract fractions with common denominators.
To subtract another fraction from one fraction, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged.
For example, let's find the value of the expression 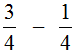 . To solve this example, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged. Let's do that:
. To solve this example, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged. Let's do that:
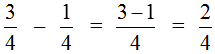
This example can be easily understood if you think of a pizza that is divided into four parts. If you cut off ![]() of the pizza from
of the pizza from ![]() of the pizza, you get
of the pizza, you get ![]() of the pizza:
of the pizza:
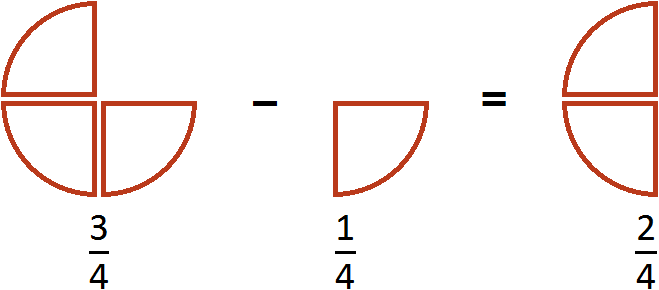
Example 2. Find the value of the expression 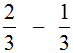 .
.
Again, we subtract the numerator of the second fraction from the numerator of the first fraction and leave the denominator unchanged:
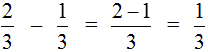
This example can be easily understood if you think of a pizza that is divided into three parts. If you cut off ![]() of the pizza from
of the pizza from ![]() of the pizza, you get
of the pizza, you get ![]() of the pizza:
of the pizza:
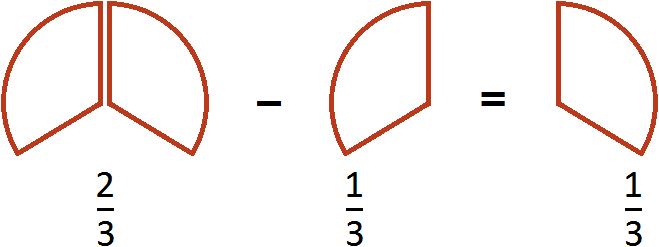
Example 3. Find the value of the expression 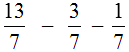
This example is solved in the same way as the previous ones. From the numerator of the first fraction subtract the numerators of the other fractions:
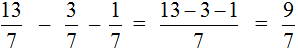
The answer is an improper fraction. Let's separate the whole part of the fraction:
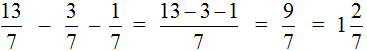
As you can see, there is nothing complicated about subtracting fractions with equal denominators. It is enough to understand the following rules:
- To subtract another fraction from one fraction, subtract the numerator of the second fraction from the numerator of the first fraction and leave the denominator unchanged;
- If the answer is an improper fraction, you need to select the whole part of it.
Subtracting fractions with different denominators
Now let's learn how to subtract fractions with different denominators. When fractions are subtracted, their denominators should be the same. But they are not always the same.
For example, you can subtract ![]() from fraction
from fraction ![]() because these fractions have the same denominators. But you cannot subtract
because these fractions have the same denominators. But you cannot subtract ![]() from fraction
from fraction ![]() because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
The common denominator is found using the same principle we used when adding fractions with different denominators. First, we find the LCM of the denominators of both fractions. Then we divide the LCM by the denominator of the first fraction and obtain the first additional multiplier, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction to obtain the second additional multiplier, which is written over the second fraction.
The fractions are then multiplied by their additional multipliers. As a result of these operations, fractions with different denominators are converted to fractions with the same denominators. And we already know how to subtract such fractions.
Example 1. Find the value of the expression: 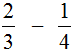
These fractions have different denominators, so you need to reduce them to the same (common) denominator.
First, find the LCM of the denominators of both fractions. The denominator of the first fraction is number 3, and the denominator of the second fraction is number 4. The least common multiple of these numbers is 12
LCM (3 and 4) = 12
Now back to fractions ![]() and
and ![]()
Find the additional factor for the first fraction. To do this, divide the LCM by the denominator of the first fraction. LCM is 12, and the denominator of the first fraction is 3. We divide 12 by 3 and get 4. Write the four above the first fraction:
![]()
Do the same with the second fraction. Divide the LCM by the denominator of the second fraction. LCM is 12, and the denominator of the second fraction is 4. Divide 12 by 4, and we get 3. Write the three above the second fraction:
![]()
Now we are ready for subtraction. It remains to multiply the fractions by their additional multipliers:
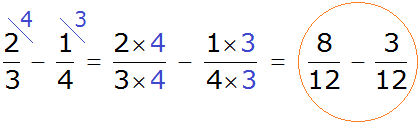
We found that fractions with different denominators turned into fractions with the same denominators. And we already know how to subtract such fractions. Let's solve this example to the end:
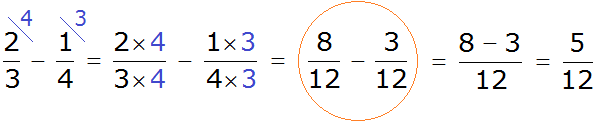
We got the answer.![]()
Let's try to represent our solution with a picture. If you cut off ![]() of a pizza from
of a pizza from ![]() pizza, you get
pizza, you get ![]() of a pizza
of a pizza
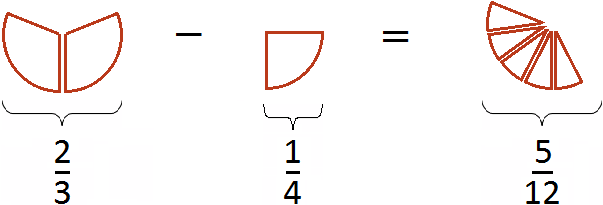
This is the detailed version of the solution. If we were in school, we would have to solve this example in a shorter form. The solution would look like this:
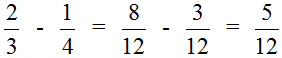
Fraction reduction ![]() and
and ![]() to a common denominator can also be represented using the figure. By reducing these fractions to a common denominator, we obtained fractions
to a common denominator can also be represented using the figure. By reducing these fractions to a common denominator, we obtained fractions ![]() and
and ![]() . These fractions will be represented by the same pieces of pizza, but this time they will be divided into the same fractions (reduced to the same denominator):
. These fractions will be represented by the same pieces of pizza, but this time they will be divided into the same fractions (reduced to the same denominator):
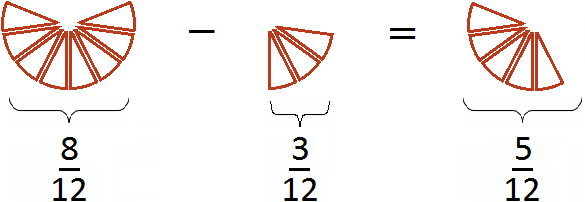
The first figure depicts a fraction![]() (eight pieces out of twelve), and the second drawing is a fraction
(eight pieces out of twelve), and the second drawing is a fraction ![]() (three slices out of twelve). By cutting off three slices from eight slices we get five slices from twelve. Fraction
(three slices out of twelve). By cutting off three slices from eight slices we get five slices from twelve. Fraction ![]() and describes these five pieces.
and describes these five pieces.
Example 2. Find the value of the expression 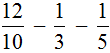
These fractions have different denominators, so we first need to reduce them to the same (common) denominator.
Find the LCM of the denominators of these fractions.
The denominators are 10, 3, and 5. The least common multiple of these numbers is 30
LCM (10, 3, 5) = 30
Now find the additional multipliers for each fraction. To do this, divide the LCM by the denominator of each fraction.
Find the additional factor for the first fraction. LCM is 30, and the denominator of the first fraction is 10. Divide 30 by 10, and we get the first additional factor 3. Write it over the first fraction:
![]()
Now find the additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is 30, and the denominator of the second fraction is 3. Dividing 30 by 3, we get the second additional factor 10. Write it over the second fraction:
![]()
Now find the additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is 30, and the denominator of the third fraction is 5. Divide 30 by 5, and we get the third additional factor 6. Write it over the third fraction:
![]()
Now everything is ready for subtraction. It remains to multiply the fractions by their additional multipliers:
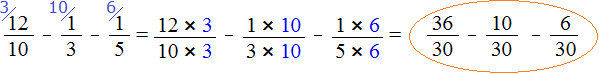
We found that fractions with different denominators turned into fractions with the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.
The continuation of the example won't fit on one line, so we move the continuation to the next line. Don't forget the equal sign (=) on the new line:
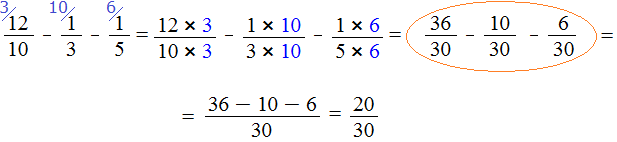
The answer is a proper fraction, and we seem to be fine with it, but it's too cumbersome and ugly. We should make it simpler. What can we do? We could shorten the fraction.
To reduce the fraction ![]() , divide its numerator and denominator by the greatest common divisor (GCD) of 20 and 30.
, divide its numerator and denominator by the greatest common divisor (GCD) of 20 and 30.
So, we find the GCD of numbers 20 and 30:
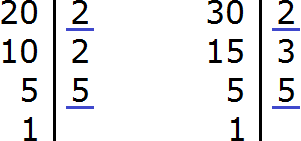
![]()
Now go back to our example and divide the numerator and denominator of the fraction ![]() by the found GCD, that is, by 10
by the found GCD, that is, by 10
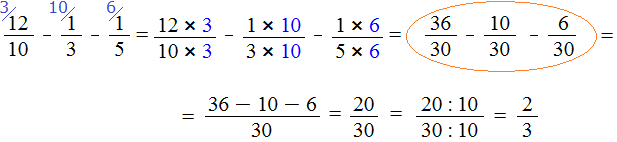
We got the answer ![]()
Multiplication of fractions with whole numbers
To multiply a fraction by a number, multiply the numerator of the fraction by that number and leave the denominator unchanged.
Example 1. Multiply a fraction ![]() by the number 1.
by the number 1.
Multiply the numerator of the fraction ![]() by the number 1.
by the number 1.
![]()
The entry![]() can be understood as taking half 1 time. For example, if you take
can be understood as taking half 1 time. For example, if you take ![]() a pizza once, you get
a pizza once, you get ![]() pizzas
pizzas
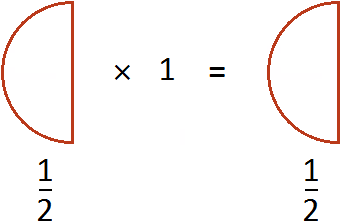
We know from the laws of multiplication that if the multiplier and the factor are swapped, the product will not change. If ![]() is written as
is written as ![]() , then the product is still
, then the product is still ![]() . Again, the rule of multiplication of a whole number and a fraction is triggered:
. Again, the rule of multiplication of a whole number and a fraction is triggered:
![]()
This entry can be understood as taking half of one. For example, if there is 1 whole pizza and we take half of it, we have ![]() a pizza:
a pizza:
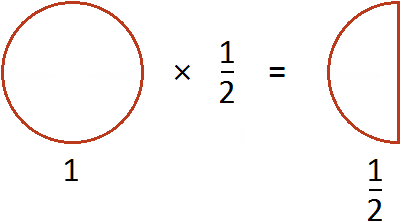
Example 2. Find the value of the expression ![]()
Multiply the numerator of the fraction ![]() by 4
by 4
![]()
The answer is an improper fraction. Let's separate the whole part of the fraction:
![]()
The expression ![]() can be understood as taking two quarters four times. For example, if you take
can be understood as taking two quarters four times. For example, if you take ![]() of a pizza 4 times, you get two whole pizzas
of a pizza 4 times, you get two whole pizzas
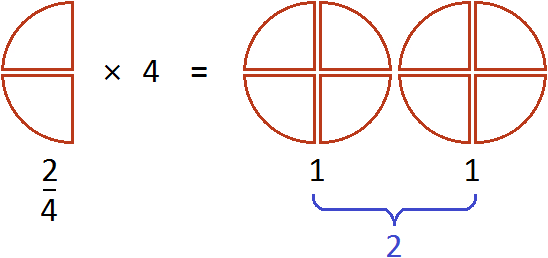
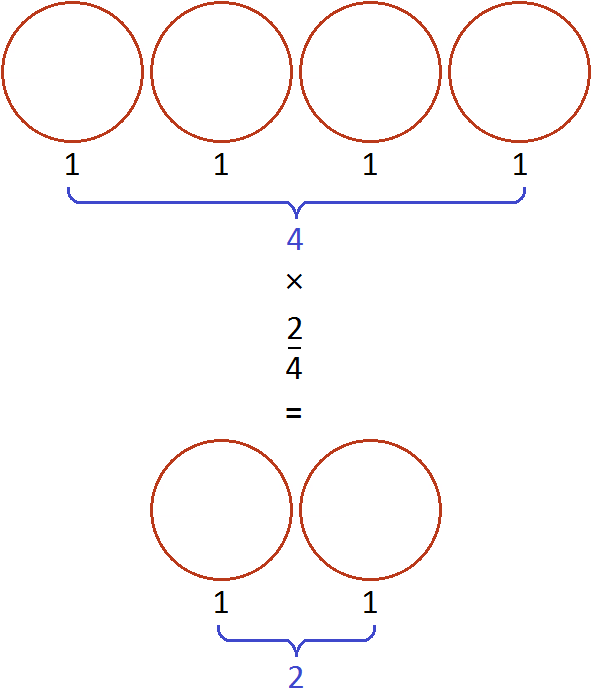
And if we swap the multiplier and the factor, we get the expression ![]() . It also equals 2. This expression can be understood as taking two pizzas from four whole pizzas:
. It also equals 2. This expression can be understood as taking two pizzas from four whole pizzas:
The number that is multiplied by a fraction and the denominator of the fraction are allowed to be reduced if they have a common divisor greater than one.
For example, the expression ![]() can be calculated in two ways.
can be calculated in two ways.
First method. Multiply 4 by the numerator of the fraction and leave the denominator unchanged:
![]()
The second way. The multiplied foursome and the foursome in the denominator of the fraction ![]() , can be reduction. These fours can be reduced by 4, because the greatest common divisor of two fours is the fourself:
, can be reduction. These fours can be reduced by 4, because the greatest common divisor of two fours is the fourself:
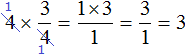
We get the same result 3. After reducing the fours, new numbers are formed in their place: two ones. But multiplying one with three and then dividing by one does not change anything. Therefore, the solution can be written in a shorter form:
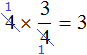
Reduction can be performed even when we choose to use the first method, but at the stage of multiplying the number 4 and the numerator 3 we choose to use reduction:
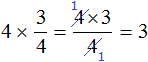
But for example, the expression ![]() can only be calculated by the first method - multiplying the number 7 by the numerator of the fraction
can only be calculated by the first method - multiplying the number 7 by the numerator of the fraction ![]() , and leaving the denominator unchanged:
, and leaving the denominator unchanged:
![]()
This is due to the fact that the number 7 and the denominator of the fraction ![]() have no common divisor greater than one, and therefore do not reduce.
have no common divisor greater than one, and therefore do not reduce.
Some students mistakenly abbreviate the multiplied number and the numerator of a fraction. This should not be done. For example, the following entry is not correct:
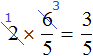
The reduction of a fraction implies that both the numerator and the denominator will be divided by the same number. In the case of 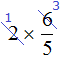 , only the numerator is divided, because writing
, only the numerator is divided, because writing 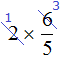 is the same as writing
is the same as writing 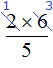 . We see that division is performed only in the numerator, and there is no division in the denominator.
. We see that division is performed only in the numerator, and there is no division in the denominator.
Multiplication of fractions
To multiply fractions, multiply their numerators and denominators. If the answer is an improper fraction, select the whole part of the fraction.
Example 1. Find the value of the expression ![]() .
.
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
![]()
The answer is ![]() . It is desirable to reduce this fraction. Fraction
. It is desirable to reduce this fraction. Fraction ![]() can be reduced by 2. Then the final solution will look like this:
can be reduced by 2. Then the final solution will look like this:
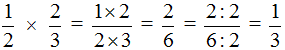
The expression ![]() can be understood as taking
can be understood as taking ![]() of a pizza from half a pizza. Suppose we have half a pizza:
of a pizza from half a pizza. Suppose we have half a pizza:

How do you take two thirds of that half? First you have to divide that half into three equal parts:

And take from these three pieces two:

We will have ![]() of a pizza. Remember what a pizza looks like divided into three parts:
of a pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will be the same size:
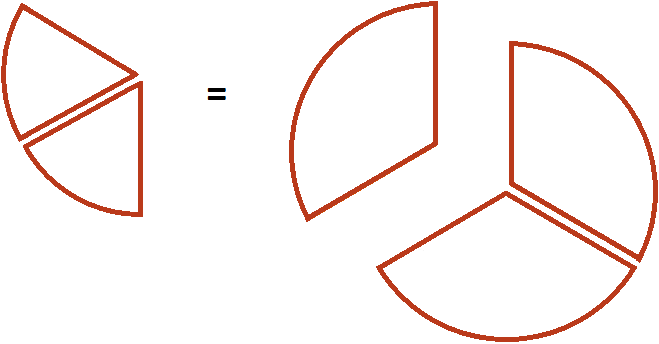
In other words, we are talking about the same size of pizza. Therefore, the value of the expression ![]() is
is ![]()
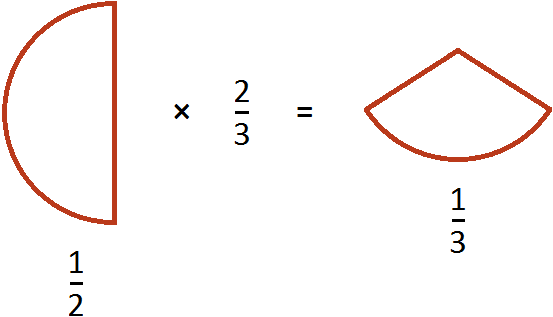
Example 2. Find the value of the expression ![]()
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
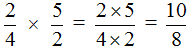
The answer is an improper fraction. Let's separate the whole part of the fraction:
![]()
Example 3. Find the value of the expression ![]()
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
![]()
The answer is a proper fraction, but it would be good if it were shortened. To reduce this fraction, divide the numerator and denominator of the fraction by the greatest common divisor (GCD) of the numbers 105 and 450.
So, let's find the GCD of 105 and 450:
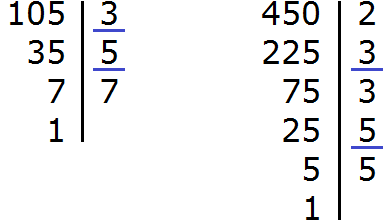
![]()
Now divide the numerator and denominator of our answer by the GCD we have now found, that is, by 15
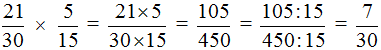
Representing a whole as a fraction
Any whole can be represented as a fraction. For example, the number 5 can be represented as ![]() . This will not change the value of five, because
. This will not change the value of five, because ![]() means "the number five divided by one," and this, as we know, equals five:
means "the number five divided by one," and this, as we know, equals five:
![]()
Inverse numbers
Now we are going to learn about a very interesting topic in math. It is called "inverse numbers".
Definition. The inverse of a is a number which, when multiplied by a, yields one.
Let's substitute the number 5 in place of the variable a in this definition and try to read the definition:
The inverse of 5 is a number that, when multiplied by 5, gives one.
Is it possible to find a number that, when multiplied by 5, gives one? It is possible. Let's represent five as a fraction:
![]()
Then multiply this fraction by itself, but swap the numerator and denominator. In other words, multiply fraction ![]() by itself, only inverted:
by itself, only inverted:
![]()
What is the result of this? If we continue to solve this example, we will get one:
![]()
So the inverse of the number 5, is the number ![]() , because multiplying 5 by
, because multiplying 5 by ![]() results in one.
results in one.
The inverse can also be found for any other whole.
Examples:
- the inverse of number 2 is the fraction

- the inverse of number 2 is the fraction

- the inverse of number 2 is the fraction

It is also possible to find an inverse number for any other fraction. To do that, all you have to do is turn it over.
Examples:
- For fraction
 the inverse fraction is fraction
the inverse fraction is fraction 
- For fraction
 the inverse fraction is fraction
the inverse fraction is fraction 
- For fraction
 the inverse fraction is fraction
the inverse fraction is fraction 
Dividing a fraction by a whole number
Let's say we have half a pizza:

Divide it equally between the two of us. How much pizza do we each get?
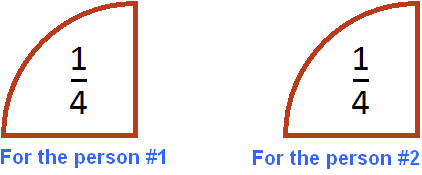
You can see that after splitting half of the pizza, there are two equal slices, each of which is ![]() of a pizza. So each person gets
of a pizza. So each person gets ![]() of a pizza.
of a pizza.
Division of fractions is done with inverse numbers. Inverse numbers allow you to replace division with multiplication.
To divide a fraction by a number, multiply the fraction by the number inverse of the divisor.
Using this rule, let's write down the division of our pizza half into two parts.
So, you want to divide fraction ![]() by number 2. Here the divisor is fraction
by number 2. Here the divisor is fraction ![]() , and the divisor is number 2.
, and the divisor is number 2.
To divide a fraction ![]() by 2, multiply the fraction by the inverse of the divisor of 2. The inverse of the divisor of 2 is
by 2, multiply the fraction by the inverse of the divisor of 2. The inverse of the divisor of 2 is ![]() . So multiply
. So multiply ![]() by
by ![]() .
.
![]()
The answer is ![]() . So when you divide half by two you get a quarter.
. So when you divide half by two you get a quarter.
Let us try to understand the mechanism of this rule. To do this, consider the following simple example. Suppose we have one whole pizza:

Let's multiply it by 2. That is, we repeat it twice (or take it twice). As a result, we will have two pizzas:
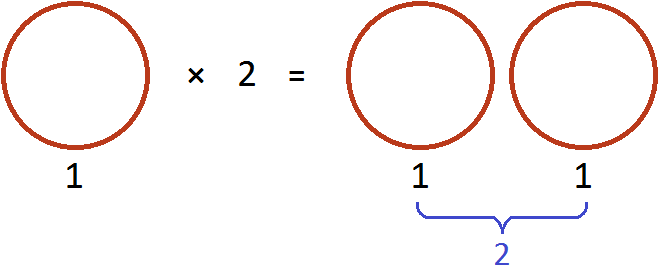
Now let's serve these pizzas to two friends. That is, divide the two pizzas by two. Then everyone gets one pizza:
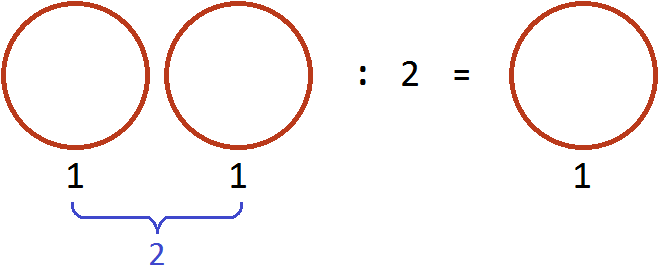
Dividing two pizzas by 2 is like taking half of those pizzas, that is, multiplying the number 2 by a fraction of ![]()
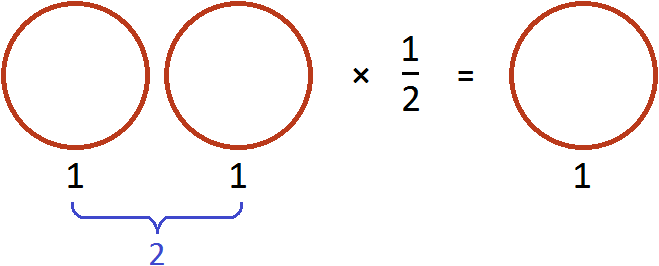
In both cases the result was the same.
The same thing happened when we divided half the pizza into two parts. To divide ![]() by 2, we multiplied that fraction by the number inverse of the divisor of 2. And the inverse of the divisor of 2 is
by 2, we multiplied that fraction by the number inverse of the divisor of 2. And the inverse of the divisor of 2 is ![]() .
.
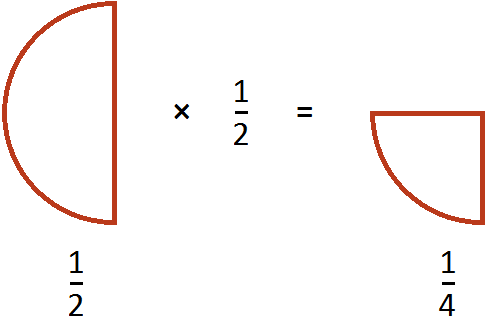
Example 2. Find the value of the expression ![]()
Multiply the first fraction by the number inverse of the divisor:
![]()
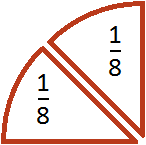
Let's say you have a quarter of a pizza and need to divide it between two people:

If you divide that quarter into two pieces, each resulting piece is one-eighth of a whole pizza:
Replacing division with multiplication is possible not only when working with fractions, but also with regular numbers. For example, we all know that 10 divided by 2 is 5.
10 : 2 = 5
In this example, replace division with multiplication. To divide the number 10 by the number 2, you can multiply the number 10 by the inverse of the number 2. And the inverse of 2 is fraction of ![]()
![]()
As you can see the result has not changed. We got the answer 5 again.
It can be concluded that division can be replaced by multiplication, provided that the inverse number is substituted for the divisor.
Example 3. Find the value of the expression ![]()
Multiply the first fraction by the number inverse of the divisor. The inverse of the divisor is a fraction of ![]()
![]()
Let's say there was ![]() of a pizza:
of a pizza:

How do you divide a pizza like this between six people? If you divide each of the three slices in half, you get six equal slices

These six pieces are six pieces of twelve. And one of those pieces is ![]() . Therefore, when you divide
. Therefore, when you divide ![]() by 6, you get
by 6, you get ![]()
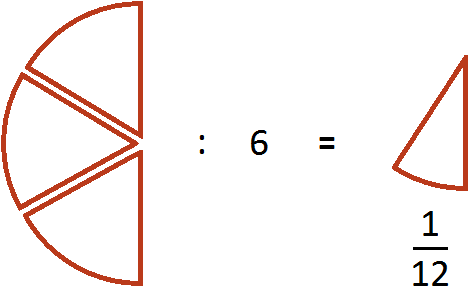
Dividing a whole number by a fraction
The rule for dividing a number by a fraction is the same as the rule for dividing a fraction by a number.
To divide a number by a fraction, multiply the number by the fraction inverse of the divisor.
For example, divide the number 1 by ![]() .
.
To divide the number 1 by ![]() , you must multiply the number 1 by the fraction inverse of the fraction
, you must multiply the number 1 by the fraction inverse of the fraction ![]() . And the inverse of fraction
. And the inverse of fraction ![]() is fraction
is fraction ![]() .
.
![]()
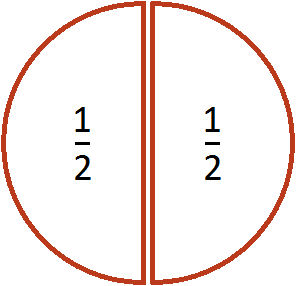
The expression ![]() can be understood as defining the number of halves in one whole pizza. Suppose there is one whole pizza:
can be understood as defining the number of halves in one whole pizza. Suppose there is one whole pizza:

If we ask the question "how many times is half contained in this pizza", the answer is 2. Indeed, half is contained in one whole pizza twice
Example 2. Find the value of the expression ![]()
Multiply 2 by a fraction the inverse of the divisor. And the inverse of the divisor is the fraction ![]()
![]()
Let's say we have two whole pizzas:
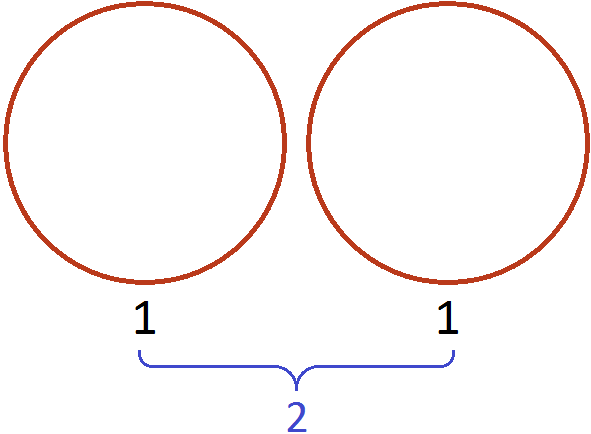
If we ask the question "how many times half is in two pizzas", the answer is 4. Indeed, half is contained in two pizzas four times:
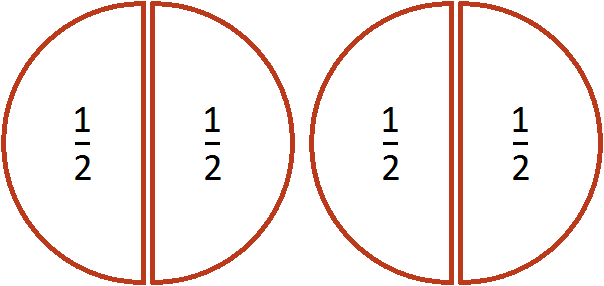
Dividing fractions
To divide a fraction by a fraction, multiply the first fraction by the fraction inverse of the second fraction.
For example, divide ![]() by
by ![]()
To divide ![]() by
by ![]() , you have to multiply
, you have to multiply ![]() by a fraction that is the inverse of a fraction of
by a fraction that is the inverse of a fraction of ![]() . And the inverse of a fraction
. And the inverse of a fraction ![]() is a fraction
is a fraction ![]()
![]()
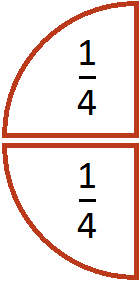
Let's say there is half a pizza:

If we ask the question "how many times a quarter of a pizza is contained in this half", the answer is 2. Indeed, a quarter of a pizza is contained in half of a pizza twice:
Example 1. Find the value of the expression ![]()
Multiply the first fraction by the fraction inverse of the second fraction. Roughly speaking, we multiply the first fraction by the inverted second fraction:
![]()
Example 2. Find the value of the expression ![]()
Multiply the first fraction by the inverse of the second fraction:
![]()
This is where you should stop and practice. Solve the few examples below. You can use the website materials as a reference. This will allow you to learn how to work with the literature.
Each next topic will be more difficult, so you need to practice.
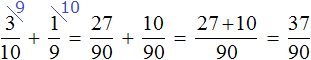
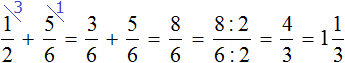
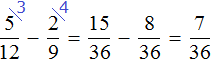
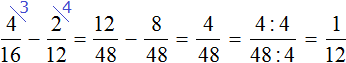
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.