Definitions and examples
A monomial is the product of numbers, variables, and powers. For example, the expressions 5a, 3ab2 and −62aa2b3 are monomials.
Here are more examples of monomials:
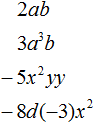
A monomial is also any single number, any variable, or any power. For example, number 9 is a monomial, variable x is a monomial, power 52 is a monomial.
Converting a monomial to the standard form
Consider the following monomial:
This monomial does not look very neat. To make it simpler, we need to reduce it to the standard form.
To reduce a monomial to the standard form is to multiply the same-type factors that make up the monomial. That is, numbers should be multiplied with numbers, variables with variables, powers with powers. As a result of these actions, we obtain a simplified monomial, which is identically equal to the previous one.
Another nuance is that powers can only be multiplied in a single term if they have the same bases.
So, let us reduce the monomial 3a25a3b2 to the standard form. This monomial contains numbers 3 and 5. Multiply them and we get number 15. Write it down:
15
Then the monomial 3a25a3b2 contains powers a2 and a3, which have the same base a. It is known from identical transformations with powers that when multiplying powers with the same base, the base is left unchanged, and the exponents are added. Then multiplication of powers a2 and a3 will result in a5. Write a5 next to number 15
15a5
Next, the monomial 3a25a3b2 contains the power of b2. There is nothing to multiply it with, so it remains unchanged. We write it as it is to the new monomial:
15a5b2
We reduced the monomial 3a25a3b2 to the standard form. As a result, we obtained the monomial 15a5b2
3a25a3b2 = 15a5b2
The numeric factor 15 is called the coefficient of the monomial. When converting a monomial to the standard form, the coefficient should be written first, and only then the variables and powers.
If there is no coefficient in a monomial, then the coefficient is said to be equal to one. Thus, the coefficient of the monomial abc is 1, since abc is the product of one and abc
abc = 1 × abc
And the coefficient of the monomial -abc is -1, because -abc is the product of minus one and abc
−abc = −1 × abc
The power of a monomial is the sum of the exponents of all the variables in the monomial.
For example, the power of the monomial 15a5b2 is 7. This is because the variable a has exponent 5, and the variable b has exponent 2. Hence 5 + 2 = 7. The exponent of the numerator 15 need not be counted, because we are interested only in the exponents of the variables.
Another example. The power of the monomial 7ab2 is 3. Here the variable a has exponent 1, and the variable b has exponent 2. Hence 1 + 2 = 3.
If a monomial does not contain variables or powers, but consists of a number, then we say that the power of such a monomial is zero. For example, the power of a monomial 11 is zero.
The power of a monomial should not be confused with the power of a number. The power of a number is the product of several identical factors, while the power of a monomial is the sum of the exponents of all variables in the monomial. There are no variables in the monomial 11, so its power is zero.
Example 1. To reduce the monomial 5xx3ya2 to the standard form
Multiply the numbers 5 and 3 to get 15. This will be the coefficient of the monomial:
15
Then the monomial 5xx3ya2 contains the variables x and x. Multiply them, and we get x2.
15x2
Next, the monomial 5xx3ya2 contains the variable y, which has nothing to multiply with. We write it down unchanged:
15x2y
Then the monomial 5xx3ya2 contains the power of a2, which also has nothing to multiply. We also leave it unchanged:
15x2ya2
We obtained the monomial 15x2ya2, which is reduced to the standard form. Alphabetic factors are usually written in alphabetical order. Then the monomial 15x2ya2 takes the form 15a2x2y.
Therefore, 5xx3ya2 = 15a2x2y.
Example 2. To reduce the monomial 2m3n × 0.4mn to the standard form
Multiply numbers, variables, and powers separately.
2m3n × 0.4mn = 2 × 0.4 × m3 × m × n × n = 0.8m4n2
Numbers, variables, and powers are allowed to be bracketed for multiplication. This is done for convenience. For example, in this example the multiplication of 2 and 0.4 can be put in brackets. Also the multiplication of m3 × m and n × n can be put in brackets.
2m3n × 0.4mn = (2 × 0.4) × (m3 × m) × (n × n) = 0.8m4n2
But it is desirable to perform all elementary actions in mind. Thus, the solution can be written down much shorter:
2m3n × 0.4mn = 0.8m4n2
But in order to be able to reduce a monomial to the standard form in your mind, the topic of multiplication of integers and multiplication of powers must be studied at a good level.
Adding and subtracting monomials
Monomials can be added and subtracted. For this to be possible, they must have the same letter part. The coefficients can be any. The addition and subtraction of monomials is essentially the reduction of like terms, which we discussed in our study of letter expressions.
To add (subtract) monomials, add (subtract) their coefficients, and leave the letter part unchanged.
Example 1. Add the monomials 6a2b and 2a2b
6a2b + 2a2b
Let's add the coefficients 6 and 2, and leave the letter part 6a2b unchanged
6a2b + 2a2b = 8a2b
Example 2. Subtract from the monomial 5a2b3 the monomial 2a2b3
5a2b3 − 2a2b3
You can replace subtraction with addition, and add the coefficients of the monomials, leaving the letter part unchanged:
5a2b3 − 2a2b3 = 5a2b3 + (−2a2b3) = 3a2b3
Or subtract the coefficient of the second monomial from the coefficient of the first monomial, and leave the letter part unchanged:
5a2b3 − 2a2b3 = 3a2b3
Multiplication of monomials
Monomials can be multiplied. To multiply monomials, you must multiply their numeric and alphabetic parts.
Example 1. Multiply the monomials 5x and 8y
Let us multiply the numeric and alphabetic parts separately. For convenience, the multipliers to be multiplied will be enclosed in brackets:
5x × 8y = (5 × 8) × (x × y) = 40xy
Example 2. Multiply the monomials 5x2y3 and 7x3y2c
Let us multiply the numeric and alphabetic parts separately. During multiplication we will apply the rule of multiplication of powers with equal bases. We will put the multiplied factors in brackets:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Example 3. Multiply the monomials −5a2bc and 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Example 4. Multiply the monomials x2y5 and (−6xy2)
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Example 5. Find the value of the expression 
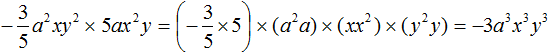
Division of monomials
A monomial can be divided by another monomial. To do this, divide the coefficient of the first monomial by the coefficient of the second monomial, and divide the letter part of the first monomial by the letter part of the second monomial. The rule of division of powers is used.
For example, divide the monomial 8a2b2 by the monomial 4ab. Write this division as a fraction:
We will call the first monomial 8a2b2 a dividend, and the second 4ab a divisor. We will call the resulting monomial the coefficient.
Divide the coefficient of the dividend by the coefficient of the divisor, we get 8 : 4 = 2. In the original expression we put an equal sign and write this coefficient of the coefficient of the coefficient:
Now divide the letter part. The dividend contains a2, the divisor contains just a. Divide a2 by a, we get a, because a2 : a = a2 - 1 = a. We write in the coefficient a after 2
Next, the dividend contains b2, the divisor contains just b. We divide b2 by b, we get b, because b2 : b = b2 - 1 = b. We write in the coefficient b after a
So, dividing the monomial 8a2b2 by the monomial 4ab results in the monomial 2ab.
You can check right away. When you multiply the coefficient by the divisor, you should get the dividend. In our case, if 2ab is multiplied by 4ab, you should get 8a2b2
2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2
It is not always possible to divide the first one by the second one. For example, if the divisor has a variable that is not in the dividend, then division is impossible.
For example, the monomial 6xy2 cannot be divided by the monomial 3xyz. The divisor 3xyz contains a variable z that is not contained in the dividend 6xy2.
Simply put, we cannot find a coefficient which, when multiplied by the divisor 3xyz, would result in a dividend of 6xy2, because that multiplication would necessarily contain a variable z that does not exist in 6xy2.
But if the dividend contains a variable that is not in the divisor, then division will be possible. In this case, the variable that was not in the divisor will be transferred to the coefficient unchanged.
For example, dividing a monomial 4x2y2z by 2xy yields 2xyz. First divide 4 by 2 to get 2, then x2 divided by x to get x, then y2 divided by y to get y. Then we proceeded to divide variable z by the same variable in the divisor, but found that there was no such variable in the divisor. So we transferred the variable z to the coefficient without changing it:
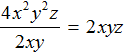
To check, multiply the coefficient 2xyz by the divisor 2xy. The result should be the monomial 4x2y2z
2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z
But in some fractions, if division is not possible, it is possible to perform reduction. This is done to simplify the expression.
Thus, in the previous example, it was impossible to divide the monomial 6xy2 by the monomial 3xyz. But it is possible to reduce this fraction by a monomial 3xy. Recall that fraction reduction is the division of the numerator and denominator by the same number (in our case, by the monominant 3xy). As a result, the fraction becomes simpler, but its value does not change:
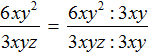
In the numerator and denominator we come to the division of the monomials, which can be done:
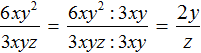
The division process is usually done in your head by writing the result above the numerator and denominator:
Example 2. Divide the monomial 12a2b3c3 by the monomial 4a2bc
Example 3. Divide the monomial x2y3z by the monomial xy2
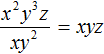
Additionally, let us mention that dividing a monomial by a monomial is also impossible if one of the powers included in the dividend has an index smaller than the index of the same power from the divisor.
For example, we cannot divide a monomial 2x by a monomial x2 because the power of x that is part of the divisor has an index of 1, while the power of x2 that is part of the divisor has an index of 2. We cannot find a coefficient that, when multiplied with the divisor x2, would result in the dividend 2x.
Of course, we can divide x by x2, using the property of the power with an integer:
and such a coefficient multiplied with the divisor x2 will result in a dividend of 2x
But so far we are interested only in those coefficients which are so-called integer expressions. Integer expressions are those expressions that are not fractions, the denominator of which contains a letter expression. And a coefficient 
is not an integer expression. It is a fractional expression with a letter expression in the denominator.
Expanding a monomial to a power
A monomial can be raised to a power. To do this, use the Power of a Power Rule (Exponents).
Example 1. Raise the monomial xy to the second power.
To raise the monominant xy to the second power, you must raise to the second power each factor of this monominant
(xy)2 = x2y2
Example 2. Raise the monomial −5a3b to the second power.
(−5a3b)2 = (−5)2 × (a3)2 × b2 = 25a6b2
Example 3. Raise the monomial −a2bc3 to the fifth power.
In this example, the coefficient of the monomial is -1. This coefficient must also be raised to the fifth power:
(−a2bc3)5 = (−1)5 × (a2)5 × b5 × (c3)5 = −1a10b5c15 = −a10b5c15
When the coefficient is equal to -1, the unit itself is not written down. Only the minus and then the other factors of the monomial are written down. In the above example we first obtain the monomial −1a10b5c15, then it was replaced by the identically equal monomial −a10b5c15.
Example 4. Present the monomial 4x2 as a squared monomial.
In this example, we need to find a product that is equal to 4x2 in the second power. Obviously, it is the product of 2x. If this product is raised to the second power (squared), then we get 4x2
(2x)2 = 22x2 = 4x2
So 4x2 = (2x)2. The expression (2x)2 is a squared monomial.
Example 5. Represent the monomial 121a6 as a squared monomial.
Let's try to find a product that is equal to the expression 121a6 in the second power.
First of all, note that number 121 is obtained if number 11 is squared. That is, we found the first factor of the future product. The power of a6 is obtained by squaring the power of a3. Thus the second factor of the future product is a3.
Thus, if the product of 11a3 is squared to the second power we obtain 121a6
(11a3)2 = 112 × (a3)2 = 121a6
So 121a6 = (11a3)2. The expression (11a3)2 is the squared monomial.
Decomposition of a monomial into factors
Since a monomial is the product of numbers, variables, and powers, it can be decomposed into the factors it consists of.
Example 1. Decompose the monomial 3a3b2 into factors
This monomial can be decomposed into the factors 3, a, a, a, b, b
3a3b2 = 3aaabb
Either the power of b2 does not need to be decomposed into the factors b and b
3a3b2 = 3aaab2
Either the power of b2 can be decomposed into the factors b and b, and the power of a3 can be left unchanged.
3a3b2 = 3a3bb
How to represent the monomial depends on the task to be solved. The main thing is that the decomposition must be identically equal to the original monomial.
Example 2. Decompose the monomial 10a2b3c4 into factors.
Decompose coefficient 10 into factors 2 and 5, decompose power a2 into factors aa, decompose power b3 into factors bbb, and decompose power c4 into factors cccc
10a2b3c4 = 2 × 5 × aabbbcccc
to the standard form.
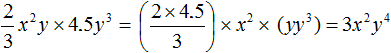
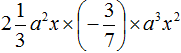to the standard form.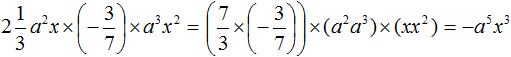
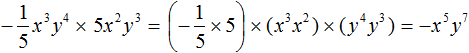
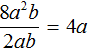
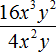
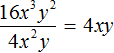
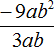
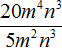
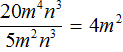
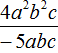
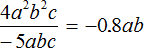
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.