Polynomials

Definitions and examples

A polynomial is the sum of monomials.

For example, the expression 2x + 4xy² + x + 2xy² is a polynomial. Simply put, a polynomial is several monomials connected by a plus sign.

In some polynomials, monomials can be joined by a minus sign. For example, 3x - 5y - 2x. Keep in mind that this is still the sum of monomials. The polynomial 3x - 5y - 2x is the sum of monomials 3x, -5y and - 2x, that is 3x + (-5y) + (-2x). After opening brackets the polynomial 3x - 5y - 2x is formed.

3x + (−5y) + (−2x) = 3x − 5y − 2x

Accordingly, when considering each monomial of a polynomial separately, it should be considered together with the sign that is placed in front of it. Thus, in the polynomial 3x - 5y - 2x, the minus before the monomial 5y refers to the quotient 5, and the minus before the monomial 2x refers to the quotient 2. To not contradict the definition of the polynomial, subtraction can be replaced with addition:

3x − 5y − 2x = 3x + (−5y) + (−2x)

But this action overloads the polynomial with brackets, so subtraction is not replaced by addition, given that in the future each monomial of the polynomial will be considered together with the sign that is placed in front of it

The monomials that make up a polynomial are called polynomial terms.

If a polynomial consists of two terms, then such a polynomial is called a binomial. For example, the polynomial x + y is a binomial.

If a polynomial has three terms, then such a polynomial is called a trinomial. For example, a polynomial x + y + z is a trinomial.

If any polynomial contains a regular number, then that number is called a free term of the polynomial. For example, in the polynomial 3x + 5y + z + 7, the term 7 is a free term. The free term of a polynomial contains no letter part.

A polynomial is also any numeric expression. Thus, the following expressions are polynomials:

2 + 3

5 + 3 + 2

5 − 4 + 9

---

Adding polynomials

You can add another polynomial to a polynomial. For example, add a polynomial 2x + y to the polynomial 3x + y.

Put each polynomial in brackets and connect them with a plus sign, thus indicating that we are adding polynomials:

(2x + y) + (3x + y)

Now open the brackets:

2x + y + 3x + y

The following are like terms:

2x + y + 3x + y = 5x + 2y

Thus, adding polynomials 2x + y and 3x + y results in a polynomial 5x + 2y.

Adding polynomials in columns is also allowed. To do this, write them so that like terms are located under each other, then perform addition. Let's solve the previous example in columns:

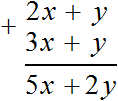
If one of the polynomials contains a term that does not have a like term in the other polynomial, it is transferred to the result without change.

For example, add the polynomials 2x² + y³ + z + 2 and 5x² + 2y³. First, write them so that like terms are located under each other, and then add them together. We find that the second polynomial does not contain any terms which can be added to the terms z and 2 of the first polynomial. Therefore the terms z and 2 are transferred to the result unchanged (together with their signs)

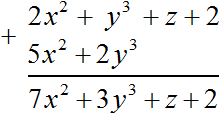
Let's solve the same example using brackets:

(2x² + y³ + z + 2) + (5x² + 2y³) = 2x² + y³ + z + 2 + 5x² + 2y³ = (2x² + 5x²) + (y³ + 2y³) + z + 2 = 7x² + 3y³ + z + 2

---

Example 3. Add polynomials 7x³ + y + z² and x³ − z²

Let's solve this example in a column. Write the second polynomial under the first one so that like terms are located under each other:

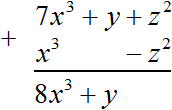
The second polynomial had no term that could be added to the y term from the first polynomial, so this term was transferred to the result unchanged. And addition of like terms z² and -z² gave 0 as a result. By tradition, we do not write down zero. Therefore, the final answer is 8x³ + y.

Let's solve the same example using brackets:

(7x³ + y + z²) + (x³ − z²) = 7x³ + y + z² + x³ − z² = (7x³ + x³) + (z² − z²) + y = 8x³ + y

---

Subtracting polynomials

You can subtract another polynomial from a polynomial. For example, subtract a polynomial 2x + y by a polynomial 3x + y.

Put each polynomial in brackets and connect them with a "minus" sign, thus indicating that we are subtracting:

(2x + y) − (3x + y)

Now let's open the brackets:

2x + y − 3x − y

Let us give like terms. The terms y and -y are opposite. The sum of the opposite terms is zero

y + (−y) = 0

Given like terms, we usually add them up. But we can use the sign of a monomial as the sign of the operation. So, by adding like terms y and -y we add them by the rule of adding like terms. But we can write them one after another without adding them

y − y

The same result will be obtained since the expressions y + (-y) and y - y are equally equal to zero:

y − y = 0

Let's go back to our example. We cross out the terms y and -y:

And addition of like terms 2x and -3x, will result in -x

2x + (−3x) = −x

Or without addition, by writing the terms one after the other:

2x − 3x = −x

So, if you subtract a polynomial (2x + y) from a polynomial (3x + y), you get a monomial -x.

Let's solve the same example in a column:

---

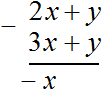
Example 2. Subtract from a polynomial 13x - 11y + 10z a polynomial -15x + 10y - 15z

Let's solve this example using brackets and then in columns:

(13x − 11y + 10z) − (−15x + 10y − 15z) = 13x − 11y + 10z + 15x − 10y + 15z = (13x + 15x) + (−11y − 10y) + (10z + 15z) = 28x + (−21y) + 25z = 28x − 21y + 25z

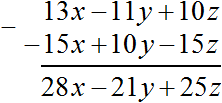
You must be careful when subtracting in columns. If you don't pay attention to the signs, you are very likely to make a mistake. It is necessary to consider not only the sign of the subtraction operation, but also the sign in front of the summand.

So, in this example, the summand -15z was subtracted from the summand 10z

10z − (−15z)

The result of calculating this expression must be positive, because 10z - (-15z) = 10z + 15z.

When adding or subtracting polynomials with brackets, the first polynomial may not be put in brackets. For example, in this example we wanted to subtract -15x + 10y + 10y - 15z from a polynomial 13x - 11y + 10z

The subtraction was written as follows:

(13x − 11y + 10z) − (−15x + 10y − 15z)

But you can leave the first polynomial out of the brackets:

13x − 11y + 10z − (−15x + 10y − 15z)

Putting the first polynomial in brackets at first allows beginners to visually see that the second polynomial is completely subtracted from the first polynomial, not from a certain part of it.

---

Representing a polynomial as a sum or a difference

A polynomial can be represented as a sum or difference of polynomials. This is essentially the inverse of opening brackets, because the idea implies that there is a polynomial, and from it we can form a sum or difference of polynomials by putting some of the terms of the original polynomial into brackets.

Let have a polynomial 3x + 5y + z + 7. Let us represent it as a sum of two polynomials.

So, from the terms of the original polynomial we need to form two polynomials added to each other. Let's bracket the terms 3x and 5y, and the terms z and 7. Then combine them with a plus sign

(3x + 5y) + (z + 7)

The value of the original polynomial does not change. If we open brackets in the resulting expression (3x + 5y) + (z + 7), we get the polynomial 3x + 5y + z + 7 again.

(3x + 5y) + (z + 7) = 3x + 5y + z + 7

You could also put the terms 3x, 5y, z in brackets and add this bracketed expression to the term 7

(3x + 5y + z) + 7

When representing a polynomial as a difference of polynomials, the following rule must be followed. If the terms are in brackets after the minus sign, then these terms inside the brackets must be reversed.

Let us return to the polynomial 3x + 5y + z + 7. Let's represent it as the difference of two polynomials. Let us bracket the polynomials 3x and 5y and z and 7, then combine them with a "minus" sign

(3x + 5y) − (z + 7)

But we see that the minus sign is followed by the bracketing of terms z and 7. So these terms need to be reversed. This should be done inside the brackets:

(3x + 5y) − (−z − 7)

When putting terms in brackets, we must make sure that the value of the new expression is identical to the previous expression. This explains the substitution of the signs of the terms inside the brackets. If we open brackets in expression (3x + 5y) - (-z - 7), we obtain the original polynomial 3x + 5y + z + 7.

(3x + 5y) − (−z − 7) = 3x + 5y + z + 7

In general, when representing a polynomial as a sum or a difference, the following rules can be followed:

If the brackets are preceded by a plus sign, all the terms inside the brackets are written with their own signs.

If a minus sign is put before the brackets, all terms inside the brackets are written with opposite signs.

Example 1. Represent the polynomial 3x⁴ + 2x³ + 5x² − 4 as a sum of some binomials:

(3x⁴ + 2x³) + (5x² − 4)

---

Example 2. Represent the polynomial 3x⁴ + 2x³ + 5x² − 4 as a difference of some binomials:

(3x⁴ + 2x³) − (−5x² + 4)

There was a minus in front of the second brackets, so the terms 5x² and −4 were written with opposite signs.

---

Polynomial and its standard form

A polynomial, like a monomial, can be reduced to the standard form. This results in a simplified polynomial that is easy to work with.

To reduce a polynomial to the standard form, you need to reduce like terms in the polynomial.

Like terms of a polynomial are terms that have the same letter part.

Let us reduce the polynomial 2x + 4xy² + x − xy² to the standard form. To do this, we give its like terms. Like terms in this polynomial are 2x and x, as well as 4xy² and -xy².

As a result, we got a polynomial 3x + 3xy² that has no like terms. This form of a polynomial is called a standard form polynomial.

Like a monomial, a polynomial has a power. To determine the degree of a polynomial, first reduce it to the standard form, then choose the monomial whose power is the largest of all.

In the previous example we reduced the polynomial 2x + 4xy² + x - xy² to the standard form. The result is the polynomial 3x + 3xy². It consists of two monomials. The power of the first monominant is 1, and the power of the second monominant is 3. The largest of these powers is 3. So the polynomial 3x + 3xy² is a polynomial of degree 3.

Since the polynomial 3x + 3xy² is identically equal to the previous polynomial 2x + 4xy² + x - xy², this previous polynomial is also a third power polynomial.

The power of a polynomial of the standard form is the greater of the powers of its constituent monomials..

In some polynomials, you first need to reduce the monomials in the polynomial to the standard form, and only then reduce the polynomial itself to the standard form.

For example, let us reduce the polynomial 3xx⁴ + 3xx³ − 5x²x³ − 5x²x to the standard form. This polynomial consists of monomials that are not reduced to the standard form. First, we reduce them to the standard form:

3xx⁴ + 3xx³ − 5x²x³ − 5x²x = 3x⁵ + 3x⁴ − 5x⁵ − 5x³

Now the resulting polynomial 3x⁵ + 3x⁴ − 5x⁵ − 5x³ can be reduced to the standard form. To do this we give its like terms. Like terms are 3x⁵ and -5x⁵. There are no more like terms. The terms 3x⁴ and -5x³ will be rewritten without change:

3xx⁴ + 3xx³ − 5x²x³ − 5x²x = 3x⁵ + 3x⁴ − 5x⁵ − 5x³ = −2x⁵ + 3x⁴ − 5x³

---

Example 2. The polynomial 3ab + 4cc + ab + 3c² should be reduced to the standard form.

First, we reduce the monomial 4cc of the initial polynomial to the standard form and obtain 4c²

3ab + 4cc + ab + 3c² = 3ab + 4c² + ab + 3c²

The following is a list of like terms:

3ab + 4cc + ab + 3c² = 3ab + 4c² + ab + 3c² = 4ab + 7c²

---

Example 3. Reduce the polynomial 4x² − 4y − x² + 17y − y to the standard form.

Like terms in this polynomial are 4x² and -x², and -4y, 17y, and -y. Let us give them:

4x² − 4y − x² + 17y − y = 3x² + 12y

You can use brackets to connect like terms. To do this, put similar terms in brackets, then combine the expressions in brackets with a "plus" sign.

Solve the previous example using brackets. Like terms in it were 4x² and -x², as well as -4y, 17y, and -y. We conclude them in brackets and combine them with a "plus" sign

4x² − 4y − x² + 17y − y = (4x² − x²) + (−4y + 17y − y)

Now in brackets let's perform the reduction of like terms:

4x² − 4y − x² + 17y − y = (4x² − x²) + (−4y + 17y − y) = (3x²) + (12y)

In the resulting expression (3x²) + (12y) open the brackets:

4x² − 4y − x² + 17y − y = (4x² − x²) + (−4y + 17y − y) = (3x²) + (12y) = 3x² + 12y

Of course, this approach overloads the expression, but it minimizes errors.

---

Example 4. Reduce the polynomial 12x² − 9y − 9x² + 6y + y to the standard form.

Bracket like terms and combine them with a plus sign

12x² − 9y − 9x² + 6y + y = (12x² − 9x²) + (−9y + 6y + y)

Next, we calculate the contents of the brackets:

12x² − 9y − 9x² + 6y + y = (12x² − 9x²) + (−9y + 6y + y) = (3x²) + (−2y)

Get rid of the brackets by opening them:

12x² − 9y − 9x² + 6y + y = (12x² − 9x²) + (−9y + 6y + y) = (3x²) + (−2y) = 3x² − 2y

---

Changing the order of members

Consider a binomial x - y. How can we make the -y term come first and the x term second?

A polynomial is the sum of monomials. That is, the original x - y binomial is the sum of x and -y

x + (−y)

The sum does not change by interchanging the places of the summands. Then x and -y can be swapped

−y + x

---

Example 2. Swap the terms in the -y - x binomial.

The binomial -y - x is the sum of the terms -y and -x

−y + (−x)

Then according to the permutative law of addition we obtain (-x) + (-y). Let us get rid of the brackets:

−x − y

Thus, the solution can be written in a shorter form:

−y − x = −x − y

---

Example 3. Order the terms of the polynomial x + xy³ − x² in descending order of powers.

The term xy³ has the highest power in this polynomial, then -x², and then x. Write them down in this order:

x + xy³ − x² = xy³ − x² + x

---

Multiplication of a monomial by a polynomial

A monomial can be multiplied by a polynomial. To multiply a monomial by a polynomial, multiply that monomial by each term of the polynomial and add the products obtained.

For example, multiply a monomial 3x² by a polynomial 2x + y + 5. When multiplying a monomial by a polynomial, the latter must be bracketed:

3x²(2x + y + 5)

Now multiply the monomial 3x² by each term of the polynomial 2x + y + 5. The resulting products will be added:

3x²(2x + y + 5) = 3x² × 2x + 3x² × y + 3x² × 5

Let's calculate the resulting products:

3x²(2x + y + 5) = 3x² × 2x + 3x² × y + 3x² × 5 = 6x³ + 3x²y + 15x²

Thus, multiplying a monomial 3x² by a polynomial 2x + y + 5 results in a polynomial 6x³ + 3x²y + 15x².

It is desirable to perform multiplication in mind. That way the solution is shorter:

3x²(2x + y + 5) = 6x³ + 3x²y + 15x²

In some examples, the monomial is placed after the polynomial. In this case, again, each term of the polynomial must be multiplied with the monomial and the resulting products must be added.

For example, the previous example might have been given in the following form:

(2x + y + 5) × 3x²

In this case we would multiply each term of the polynomial (2x + y + 5) by the monomial 3x² and add the results:

(2x + y + 5) × 3x² = 2x × 3x² + y × 3x² + 5 × 3x² = 6x³ + 3x²y + 15x²

The multiplication of a monomial by a polynomial (or the multiplication of a polynomial by a monomial) is based on the distributive law of multiplication.

a(b + c) = ab + ac

That is, to multiply the number a by the sum b + c, you need to multiply the number a by each summand of the sum b + c, and add the products obtained.

In general, the multiplication of a monomial by a polynomial, and the distributive law of multiplication have a geometric meaning.

Suppose there is a rectangle with sides a and b

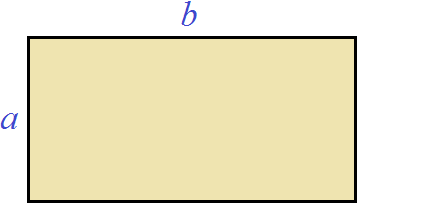
Increase the side of b by c

Let's complete the missing side and paint the resulting rectangle for clarity:

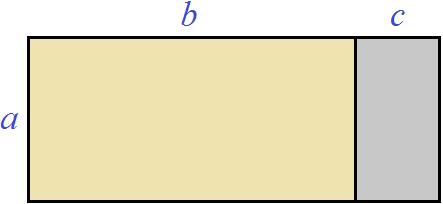
Now calculate the area of the resulting large rectangle. It includes yellow and gray rectangles.

To calculate the area of the resulting large rectangle, you can separately calculate the areas of the yellow and gray rectangles and add up the results. The area of the yellow rectangle is ab, and the area of the gray rectangle is ac

ab + ac

This is like multiplying the length of a large rectangle by its width. The length in this case is b + c, and the width is a

(b + c) × a

or width multiplied by length to arrange the letters a, b, and c in alphabetical order:

a × (b + c)

Thus, the expressions a × (b + c) and ab + ac are equal to the same value (the same area)

a × (b + c) = ab + ac

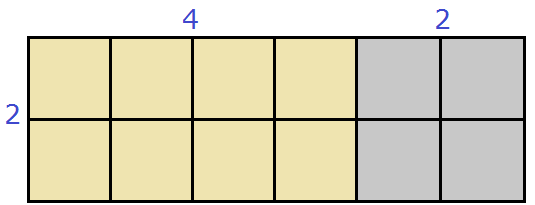
For example, suppose we have a rectangle 4 cm long and 2 cm wide, and we increase the length by 2 cm

Then the area of this rectangle is 2 × (4 + 2) or the sum of the areas of the yellow and gray rectangles: 2 × 4 + 2 × 2. The expressions 2 × (4 + 2) and 2 × 4 + 2 × 2 are equal to the same value 12

2 × (4 + 2) = 12

2 × 4 + 2 × 2 = 12

Therefore,

2 × (4 + 2) = 2 × 4 + 2 × 2 = 12.

Indeed, the resulting large rectangle contains twelve square centimeters:

---

Example 2. Multiply the monomial 2a by the polynomial a² - 7a - 3

Multiply the monomial 2a by each term of the polynomial a² - 7a - 3 and add the products obtained:

2a(a² − 7a − 3) = 2a × a² + 2a × (−7a) + 2a × (−3) = 2a³ + (−14a²) + (−6a) = 2a³ − 14a² − 6a

Or shorter:

2a(a² − 7a − 3) = 2a³ − 14a² − 6a

---

Example 3. Multiply the monomial -a²b² by the polynomial a²b² − a² − b²

Multiply the monomial -a²b² by each term of the polynomial a²b² − a² − b² and add the products obtained:

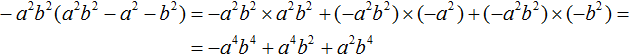
Or shorter:

---

Example 4. Perform multiplication −1.4x²y⁶(5x³y − 1,5xy² − 2y³)

Multiply the monomial -1.4x²y⁶ by each term of the polynomial 5x³y − 1,5xy² − 2y³ and add the products obtained:

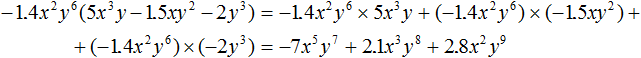
Or shorter:

---

Example 5. Perform multiplication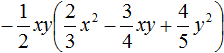

Multiply the monomial by each term of the polynomial  and add the products obtained:

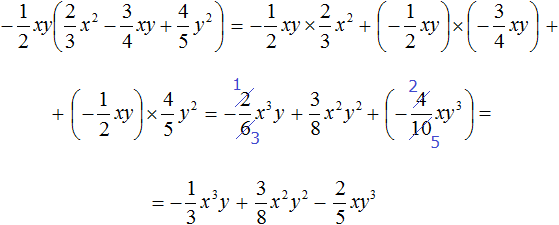
Or shorter:

When performing short solutions, the results are written one after the other along with the sign of the resulting term. Let's take a step-by-step look at how the short solution to this example was performed.

First, the monomial  must be multiplied by the first term of the polynomial , that is, by . The multiplication is done in mind. The result is . In the original expression we put an equal sign and write down the first result:

After that, no signs can be placed in the original expression. You must immediately proceed to the next multiplication.

The next step is to multiply the monomial  by the second term of the polynomial , that is, by . We get the result . This result is positive, i.e. with a plus sign . In the original expression this result is written together with this plus sign right after the term 

After that, no signs can be placed in the original expression. You must immediately proceed to the next multiplication.

The next step is to multiply the monomial  by the third term of the polynomial , that is, by . The result is . This result is negative, that is, with a minus sign. In the original expression, this result is written together with its minus right after the term 

---

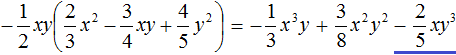
Sometimes there are expressions in which you must first multiply a monomial by a polynomial and then again by a monomial. For example:

2(a + b)c

In this example, the term 2 is first multiplied by the polynomial (a + b), then the result is multiplied by c. First, multiply 2 by (a + b) and put the result in brackets

2(a + b)c = (2a + 2b)c

The brackets indicate that the result of multiplying 2 by (a + b) is completely multiplied by c. If we had not bracketed 2a + 2b, we would have obtained the expression 2a + 2b × c, in which only 2b is multiplied by c. This would have changed the value of the original expression, and this is unacceptable.

So we got (2a + 2b)c. Now we multiply the polynomial (2a + 2b) by the monomial c and get the final result:

2(a + b)c = (2a + 2b)c = 2ac + 2bc

Multiplication could also be done by first multiplying (a + b) by c and multiplying the result with the term 2

2(a + b)c = 2(ac + bc) = 2ac + 2bc

In this case, the commutative law of multiplication comes into play, which says that if an expression consists of several factors, then the product will not depend on the order of operations:

a × b × c = (a × b) × c = a × (b × c)

That is, the multiplication can be done in any order. This will not change the value of the original expression.

---

Multiplication of a polynomial by a polynomial

To multiply a polynomial by a polynomial, multiply each term of the first polynomial by each term of the second polynomial and add the products obtained.

For example, multiply a polynomial x + 3 by y + 4

Bracket each polynomial and join them with the multiplication sign ×

(x + 3) × (y + 4)

Or write them one after another without the × sign. This will also mean multiplication:

(x + 3)(y + 4)

Now multiply each term of the first polynomial (x + 3) by each term of the second polynomial (y + 4). Here again the distributive law of multiplication will be applied:

(a + b)c= ac + bc

The difference is that instead of the variable c we have a polynomial (y + 4) consisting of terms y and 4. Our problem is to multiply (x + 3) first by y, then by 4. To make no mistake, we can pretend that term 4 doesn't exist at all yet. To do that, we can cover it with our hand:

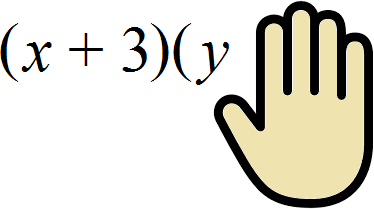
We get the usual multiplication of a polynomial by a monomial. Namely, the multiplication of a polynomial (x + 3) by a monomial y. Let us perform this multiplication:

(x + 3)(y + 4) = xy + 3y

We have multiplied (x + 3) by y. Now it remains to multiply (x + 3) by 4. To do this, multiply each term of the polynomial (x + 3) by the monomial 4. This time in the original expression (x + 3)(y + 4) hand over y, since we already multiplied the polynomial (x + 3) by it

We obtain the multiplication of the polynomial (x + 3) by the monomial 4. Let us perform this multiplication. The multiplication must be continued in the original example (x + 3)(y + 4) = xy + 3y

(x + 3)(y + 4) = xy + 3y + 4x + 12

Thus, multiplying a polynomial (x + 3) by a polynomial (y + 4) results in a polynomial xy + 3y + 4x + 12.

Another way to multiply a polynomial by a polynomial is to multiply each term of the first polynomial by the second polynomial as a whole and add the products obtained.

Solve the previous example using this method. Multiply each term of the polynomial x + 3 by the whole polynomial y + 4 and add the products obtained:

(x + 3)(y + 4) = x(y + 4) + 3(y + 4)

As a result, we come to the multiplication of a monomial by a polynomial, which we studied earlier. Let's perform this multiplication:

(x + 3)(y + 4) = x(y + 4) + 3(y + 4) = xy + 4x + 3y + 12

The result will be the same as before, but the terms of the resulting polynomial will be arranged slightly differently.

Multiplication of a polynomial by a polynomial makes geometric sense. Suppose there is a rectangle with length a and width b

The area of this rectangle is a × b.

Increase the length of the rectangle by x and the width by y

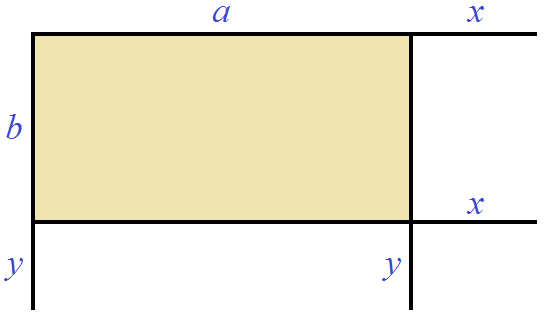
Let's finish the missing sides and paint the resulting rectangles for clarity:

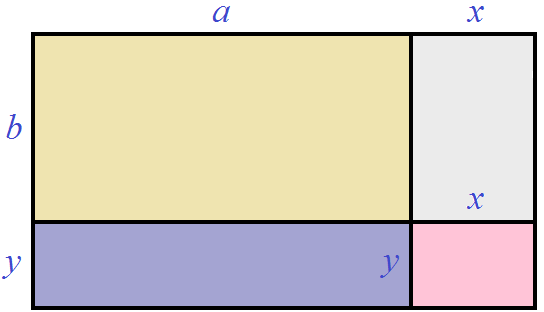
Now calculate the area of the resulting large rectangle. To do this, separately calculate the area of each rectangle included in the big rectangle and sum the results. The area of the yellow rectangle is ab, the area of the gray one is xb, the area of the purple one is ay, the area of the pink one is xy

ab + xb + ay + xy

And this is like multiplying the length of the resulting large rectangle by its width. The length in this case is a + x, and the width is b + y

(a + x)(b + y)

That is, the expressions (a + x)(b + y) and ab + xb + ay + xy are identically equal

(a + x)(b + y) = ab + xb + ay + xy

Suppose we had a rectangle that was 6 cm long and 3 cm wide, and we increased its length by 2 cm and width by 1 cm.

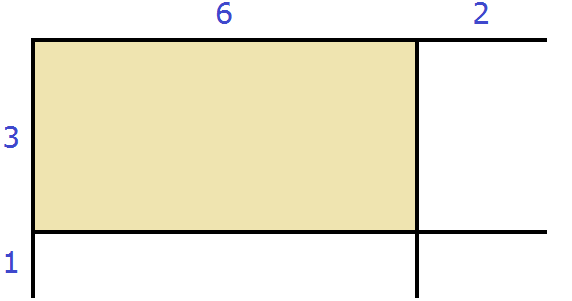
Let's finish the missing sides and paint the resulting rectangles for clarity:

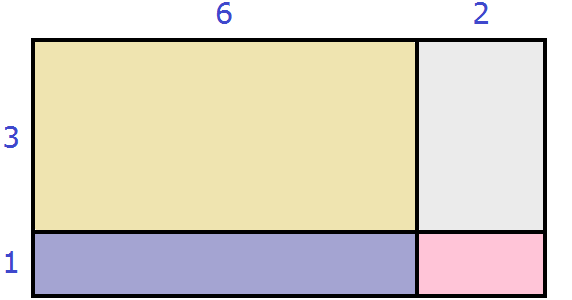
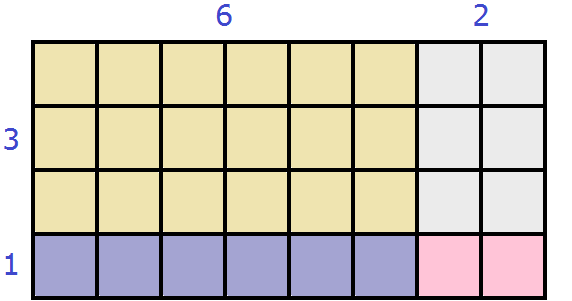
The area of the resulting large rectangle is (6 + 2)(3 + 1) or the sum of the areas of the rectangles included in the large rectangle: 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1. In both cases we obtain the same result 32

(6 + 2)(3 + 1) = 32

6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 32

Therefore,

(6 + 2)(3 + 1) = 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 18 + 6 + 6 + 2 = 32

Indeed, the resulting large rectangle contains thirty-two square centimeters:

---

Example 2. Multiply a polynomial a + b by c + d

Put the original polynomials in brackets and write them one after another:

(a + b)(c + d)

Now multiply each term of the first polynomial (a + b) by each term of the second polynomial (c + d)

(a + b)(c + d) = ac + bc + ad + bd

---

Example 4. Perform multiplication (−x − 2y)(x + 2y²)

Now multiply each term of the first polynomial (−x − 2y) by each term of the second polynomial (x + 2y²)

(−x − 2y)(x + 2y²) = −x² − 2xy − 2xy² − 4y³

The result of multiplication of terms should be written together with the signs of these terms. Consider step by step how this example was solved.

So, we need to multiply the polynomial (-x - 2y) by the polynomial (x + 2y²). First multiply the polynomial (-x - 2y) by the first term of the polynomial (x + 2y²), that is, by x.

Multiply -x by x, and you get -x². In the original expression (-x - 2y)(x + 2y²) put an equal sign and write -x²

(−x − 2y)(x + 2y²) = −x²

After that, no signs can be placed in the original expression. We must immediately proceed to the next multiplication. Namely, multiply -2y by x . The result is -2xy. This result is negative, that is, with a minus sign. In the original expression, write the result -2xy right after the term -x²

(−x − 2y)(x + 2y²) = −x² − 2xy

Now multiply the polynomial (-x - 2y) by the second term of the polynomial (x + 2y²), i.e. by 2y²

Multiply -x by 2y² to get -2xy². In the original expression, write this result right after the term -2xy

(−x − 2y)(x + 2y²) = −x² − 2xy − 2xy²

We proceed to the next multiplication. Namely, multiplying -2y by 2y². We obtain -4y³. In the original expression, write this result together with its minus right after the term -2xy²

(−x − 2y)(x + 2y²) = −x² − 2xy − 2xy² − 4y³

---

Example 5. Multiply (4a² + 2ab − b²)(2a − b)

Multiply each term of the polynomial (4a² + 2ab − b²) by each term of the polynomial (2a - b)

In the resulting expression, you can give like terms:

---

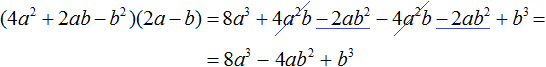
Example 6. Perform multiplication -(a + b)(c - d)

This time there is a minus in front of the brackets. This minus is the coefficient -1. That is, the original expression is the product of three factors: -1, polynomial (a + b), and polynomial (c - d).

−1(a + b)(c − d)

According to the combinative law of multiplication, if an expression consists of several factors, it can be calculated in any order.

So you can first multiply the polynomials (a + b) and (c - d) and multiply the resulting polynomial by -1. The multiplication of polynomials (a + b) and (c - d) should be done in brackets

−1(a + b)(c − d) = −1(ac + bc − ad − bd)

Now multiply -1 and the polynomial (ac + bc - ad - bd). As a result, all terms of the polynomial (ac + bc - ad - bd) will change their signs to the opposite:

−1(a + b)(c − d) = −1(ac + bc − ad − bd) = −ac − bc + ad + bd

Or you could multiply -1 with the first polynomial (a + b) and multiply the result with the polynomial (c - d)

−1(a + b)(c − d) = (−a − b)(c − d) = −ac − bc + ad + bd

---

Example 7. Perform multiplication x²(x + 5)(x − 3)

First multiply the polynomials (x + 5) and (x - 3), then multiply the resulting polynomial with x²

---

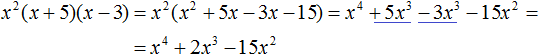
Example 8. Perform multiplication (a + 1)(a + 2)(a + 3)

First multiply the polynomials (a + 1) and (a + 2), then multiply the resulting polynomial with the polynomial (a + 3)

So, multiply (a + 1) and (a + 2)

Multiply the resulting polynomial (a² + a + 2a + 2) with (a + 3)

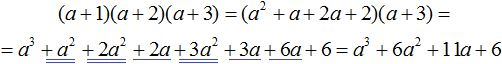
If the fast multiplication of polynomials is difficult at first, you can use the detailed solution, the essence of which is to write down how each term of the first polynomial is multiplied by the whole second polynomial. Such a notation, although it takes a lot of space, keeps errors to a minimum.

For example, multiply (a + b)(c + d)

Let us write down how each term of a polynomial a + b is multiplied by the whole polynomial c + d. As a result, we come to the multiplication of a monomial by a polynomial, which is easier to perform:

(a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd

This notation is convenient when multiplying a binomial by some polynomial that contains more than two terms. For example:

(x + y)(x² + 2xy + y²) = x(x² + 2xy + y²) + y(x² + 2xy + y²) = x³ + 2x²y + xy² + x²y + 2xy² + y³ = x³ + 3x²y + 3xy² + y³

Or when multiplying polynomials with more than two terms. For example, multiply a polynomial x² + 2x - 5 by a polynomial x³ - x + 2

(x² + 2x − 5)(x³ − x + 2)

Write the multiplication of the original polynomials as a multiplication of each term of the polynomial x² + 2x - 5 by the polynomial x³ - x + 2.

We obtained the usual multiplication of monomials by polynomials. Let us perform these multiplications:

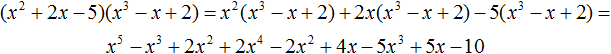
In the resulting polynomial we give like terms:

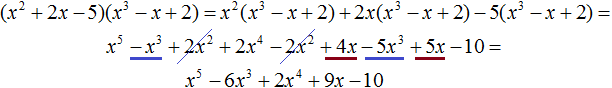
Arrange the monomials in the resulting polynomial in descending order of powers. It is not necessary to do this. But such a notation will be more beautiful:

---

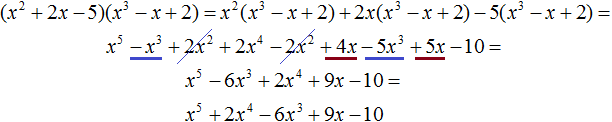
Putting the common factor out of brackets

We have already learned how to put the common factor behind brackets in simple alphabetic expressions. Now we will go a little deeper into this topic and learn how to put the common factor out of brackets in a polynomial. The principle will be the same as in a simple letter expression. Only polynomials consisting of powers will cause some difficulties.

Consider a simple binomial 6xy + 3xz. Put the common factor out of brackets. In this case the common factor 3x can be put out of brackets. Recall that if the common factor is put out of brackets, each summand of the original expression must be divided by this common factor:

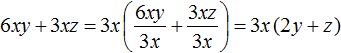
Or shorter:

The result is 3x(2y + z). In this case another simpler polynomial (2y + z) is formed in brackets. The common factor that is taken out of brackets is chosen so that the brackets contain terms that do not contain a common literal factor, and the coefficient modules of these terms have no common divisor except one.

That is why in the above example the common factor 3x was put out of brackets. A polynomial 2y + z whose coefficient modules have no common divisor except unity is formed in brackets. This requirement can be fulfilled by finding the greatest common divisor (GCD) of the coefficient modules of the original terms.This GCD becomes the coefficient of the common factor to be taken out of brackets. In our case, the original polynomial was 6xy + 3xz. The coefficients of the original terms are 6 and 3, and their GCD is 3.

And the letter part of the common factor is chosen so that the terms in brackets do not have common letter factors. In this case, this requirement was easily met. The common letter factor was visible to the naked eye - it was the x factor.

---

Example 2. Put outside the brackets the common factor in the polynomial x² + x + xy

All terms of this polynomial have a quotient of one. The greatest common divisor of the moduli of these units is one. Therefore the numerical part of the bracketed factor will be one. But one is not written as a coefficient.

Next, we choose the letter part of the common factor. First of all, we must understand that any term included in a polynomial is a monomial. And a monomial is the product of numbers, variables, and powers. Even if the term of a polynomial is an ordinary number, it can always be represented as a product of one and the number itself. For example, if a polynomial contains the number 5, it can be represented as 1 × 5. If a polynomial contains a number 8, it can be represented as a product of multipliers 2 × 2 × 2 (or as 2 × 4)

The situation is the same with variables. If a polynomial contains a term that is a variable or a degree, it can always be represented as a product. For example, if a polynomial contains a monomial term x, it can be represented as a product of 1 × x. If a polynomial contains a monomial term x³, it can be represented as a product of xxx.

The monomials that make up the polynomial x² + x + xy can be decomposed into factors so that we can see the alphabetic factor that is common to all the terms.

So, the first term of the polynomial x² + x + xy, namely x² can be represented as a product of x × x. The second term x can be represented as 1 × x. Leave the third term xy unchanged, or for clarity rewrite it with the multiplication sign x × y

Translated with www.DeepL.com/Translator (free version)

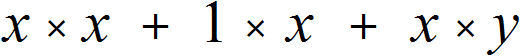
Each term of a polynomial is represented as a product of factors of which these terms consist. It is easy to see that in all three products the common factor is x. Let us distinguish it:

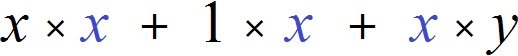
This factor x is taken out of brackets. If you put the common factor out of brackets, divide each term of the original expression by this common factor. In our case each term of the polynomial x × x + 1 × x + x × y should be divided by the common factor x

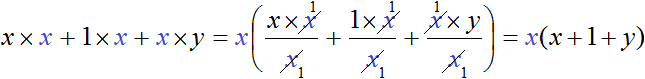
So, if you put the common factor out of brackets in the polynomial x² + x + xy, you get x(x + 1 + y)

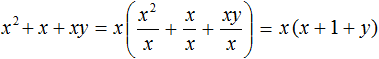
Or shorter:

As a result, the brackets contain terms that have no common literal factors, and the moduli of the coefficients of these terms have no common divisors except 1.

---

Example 2. Put the common factor out of brackets in the 15x²y³ + 12xy² + 3xy² polynomial

Determine the coefficient of the common factor taken out of brackets. The greatest common divisor of the moduli of coefficients 15, 12, and 3 is number 3. So, the number 3 is the coefficient of the common factor to be taken out of the brackets.

Now determine the letter part of the common factor to be taken out of brackets. It must be chosen so that the terms that do not contain a common letter factor remain in the brackets.

Let us rewrite the letter parts of the original polynomial 15x²y³ + 12xy² + 3xy² as a factorization. This will allow us to see well what can be taken out of the brackets:

We see that the common factor among the letter parts is xyy, that is, xy². If we take this factor out of brackets, the brackets leave a polynomial without a common letter factor.

As a result, the common factor taken out of the brackets will be the factor 3xy²

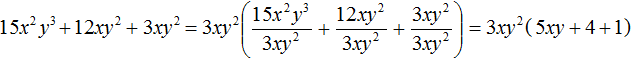
Or shorter:

To check, you can multiply 3xy²(5xy + 4 + 1). The result should be a polynomial 15x²y³ + 12xy² + 3xy²

3xy²(5xy + 4 + 1) = 3xy² × 5xy + 3xy² × 4 + 3xy² × 1 = 15x²y³ + 12xy² + 3xy²

---

Example 3. Put the common factor outside the brackets in the expression x² + x

In this case you can put x

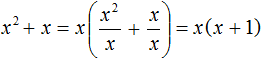
This is because the first term x² can be represented as xx. And the second term x can be represented as 1 × x

x² + x = xx + 1 × x 

It is not necessary to write out in detail the contents of each term by decomposing it into multipliers. This is easily done in your mind.

---

Example 4. Put the common factor out of brackets in the polynomial 5y² − 15y

In this case 5y can be taken out of brackets. The greatest common divisor of the moduli of coefficients 5 and 15 is number 5. Among the letter factors, the common factor is y

---

Example 5. Put the common factor out of brackets in the polynomial 5y² − 15y³

In this example, 5y² can be taken out of brackets. The greatest common divisor of the moduli of coefficients 5 and 15 is number 5. Among the letter factors, the common factor is y²

---

Example 6. Put the common factor out of brackets in the polynomial 20x⁴ − 25x²y² − 10x³

In this example, 5x² can be taken out of brackets. The greatest common divisor of the moduli of the coefficients 20, -25, and -10 is number 5. Among the letter multipliers, the common factor is x²

---

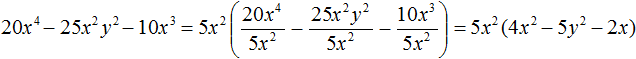
Example 7. Put the common factor out of brackets in the polynomial a^m + a^{m + 1}

The second term a^m + 1 is the product of am and a, since a^m × a = a^{m + 1}

Replace the term a^m + 1 in the original example with the identically equal product a^m × a. This makes it easier to see the common factor:

Now we can see that the common factor is a^m. We will put it out of brackets:

---

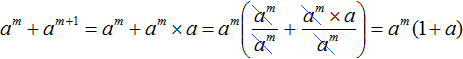
Checking for Identity

Solving a task with polynomials sometimes stretches over several lines. Each following transformation must be identically equal to the previous one. If you have doubts about the correctness of your actions, you can substitute arbitrary values of variables in the original and obtained expression. If the original expression and the resulting expression are equal to the same value, you can be sure that the task has been solved correctly.

Suppose we need to take the common factor out of brackets in the next polynomial:

2x + 4x²

In this case you can take the common multiplier 2x out of the brackets

2x + 4x² = 2x(1 + 2x)

Suppose we are not sure about such a solution. In this case, take any value of the variable x and substitute it first into the original expression 2x + 4x², then into the resulting 2x(1 + 2x). If the result is the same in both cases, it means that the task is solved correctly.

Take an arbitrary value of x and substitute it into the original expression 2x + 4x². Let x = 2. Then we get:

2x + 4x² = 2 × 2 + 4 × 2² = 4 + 16 = 20

Now substitute the value of 2 into the transformed expression 2x(1 + 2x)

2x(1 + 2x) = 2 × 2 × (1 + 2 × 2) = 4 × 5 = 20

That is, when x = 2 the expressions 2x + 4x² and 2x(1 + 2x) are equal to the same value. This means that the task was solved correctly. The same will happen for other values of the variables x. For example, check our solution when x = 1

2x + 4x² = 2 × 1 + 4 × 1² = 2 + 4 = 6
2x(1 + 2x) = 2 × 1 × (1 + 2 × 1) = 2 × 3 = 6

---

Example 2. Subtract from the polynomial 5x² - 3x + 4 the polynomial 4x² - x and check the result by substituting an arbitrary value for the variable x.

Perform the subtraction:

We performed two transformations: first we opened the brackets, and then we gave like terms. Now let us check these two transformations for identity. Let x = 2. Let us first substitute this value in the original expression and then in the transformed ones:

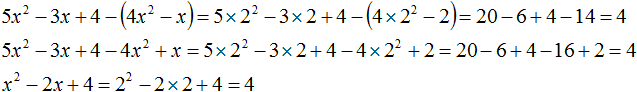
We see that for each transformation the value of the expression at x = 2 did not change. This means that the task was solved correctly.

---

Tasks for independent decision

---

Add comment

Name (required)

E-mail (required, but will not display)

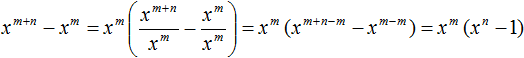
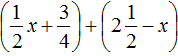
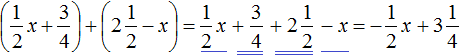
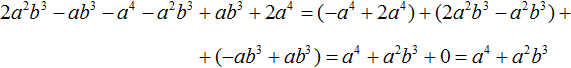
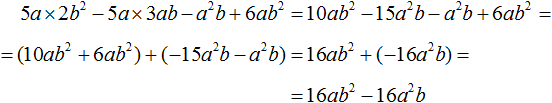
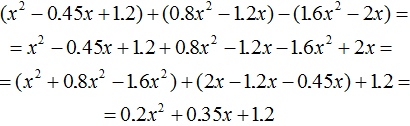
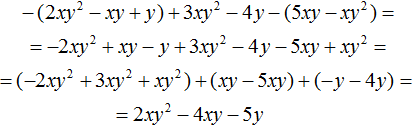
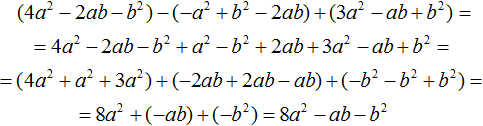
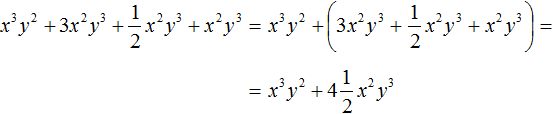
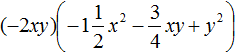
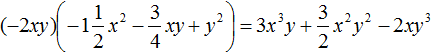
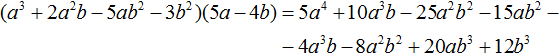
Notify me of follow-up comments

Refresh

Send

Cancel