Function y=k*x² its properties and graph

Properties of function y=x²

We plotted the graph  by points. It looked like this (see Fig. 1):

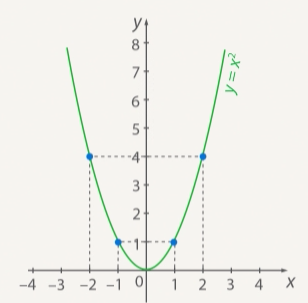
Fig. 1. Graph of the function

Note that the value of the function at any point is non-negative - this is logical, because squaring cannot result in a negative number, which means that everything under the  axis cannot belong to our graph.

Note also that this graph is symmetric with respect to the ordinate axis. There is a special name for such functions: they are called even functions. Even functions have a graph symmetric with respect to , and this is due to the fact that , like for our function.

Note also that our graph decreases before 0, and increases after 0 (see Fig. 2).

Fig. 2. Decreasing and increasing of the graph of the function

Accordingly, the greater  (at ), the greater  and the greater  (at ), the greater .

Properties of the function y=k*x² when k > 0

Now let's try to change , for now we'll take it only positive.

For example, take k=2 and k=0.5. If we plot by points, we can see that at x=0; y=0 (see Fig. 3).

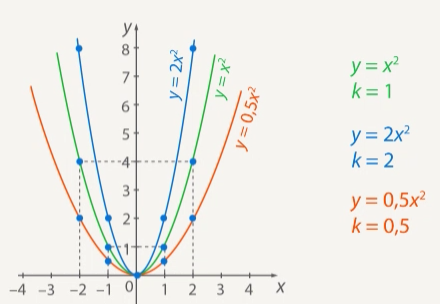
Figure 3. Graphs of the functions  (blue graph) and  (red)

Although we only gave three examples, we can already draw some conclusions about the function , at . First, the graph of such a function lies in the upper half-plane. And this is logical: if the square of a number (a non-negative number) is multiplied by a positive number , the result is non-negative.

Property 1. The set of values of function  at  is all non-negative numbers ().

Further, we note that if we substitute  into this function, we still get . Therefore we can formulate another property.

Property 2. The graph  at  is symmetric about the -axis (see Fig. 4).

Fig. 4. The parity of functions

Such functions are called even functions.

Learn more about function properties

So, we are talking about a function . Let us distinguish several properties of it.

1. Parity. A function is said to be even if for any  of its domain . For example,  is an even function.

The graph of an even function is always symmetric about the ordinate axis (see Fig. 5).

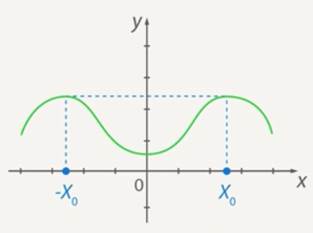
Fig. 5. Symmetry of the graph of an even function with respect to the ordinate axis

Similarly, a function is called odd if for any of its domain . In particular,  is an odd function. The graph of an odd function is symmetric with respect to the origin.

2. Monotonicity. A function is said to increase (strictly) on some interval if for any  . But if for all such : , the function decreases on this interval.

For example. . Then if , then  (since ). So the function is increasing for positive . Similarly, we prove that it decreases for negative .

The graphs and the equation of the function show that its smallest value is reached at zero and is equal to zero (indeed, the square of any other number is strictly positive). There is no largest value: the more we take modulo , the more  we get.

Property 3. The graph  at  increases for positive X and decreases for negative X (see Fig. 6).

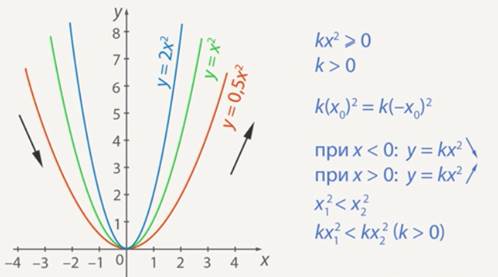
Fig. 6. Decreasing and increasing of the function 

Transformation of the graph of the function y=k*x² by changing k

What happens to the graph if we increase the number ? If we plot by points, then if we increase  by a factor of two, for example, the ordinate of a point with the same abscissa will increase by the same factor of two. That is, in theory, the graph should become narrower. And vice versa, if  decreases (leaving it positive), it will become wider (see Fig. 3). This hypothesis can be checked visually (see Fig. 7 and Fig. 8).

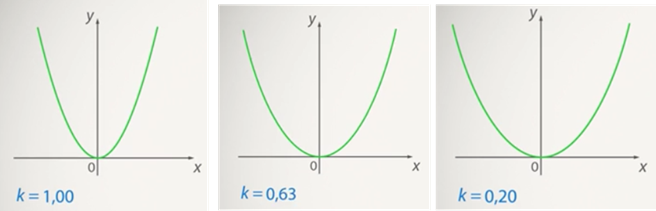
Figure 7. As  decreases, the graph expands

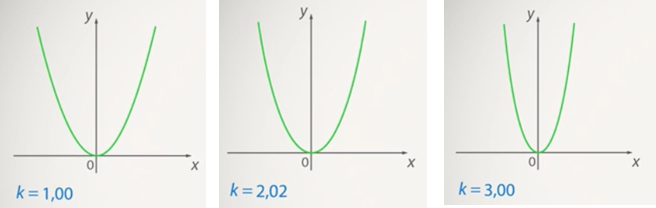
Fig. 8. As  increases, the graph narrows

Thus, keeping this property in mind, you can always plot the graph of function  depending on  by narrowing or expanding the graph of function .

Problem (k > 0)

What is the largest and smallest value of the function  on the segment  (See Figure 9.)

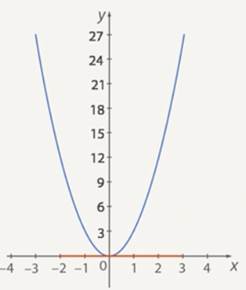
Fig. 9. The graph of the function 

Solution

Everything is clear with the smallest value: the graph (and the property) show that the smallest value is . But what about the largest value? We can see that the further the abscissa is from zero, the greater the value of the function. This makes sense: the greater the value of the function, the greater the modulus of the abscissa. So the greatest value is reached at point  and it is .

Answer: .

Properties of the function y=k*x² when k < 0

Now let's turn to negative . We can draw the function  at  by points. Or you can take, for example, the graph of , which we already know how to draw, and then multiply each value by . How do you draw a graph? Multiplying by  changes the sign of the ordinate, so essentially we just mirror the graph with respect to the abscissa axis (see Figure 10).

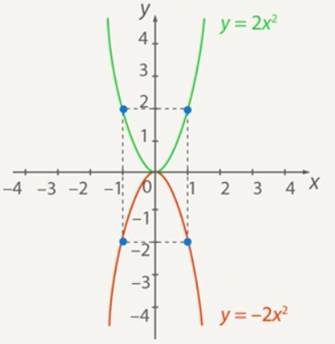
Fig. 10. Construction of the function  at 

1. Property 1. The set of values of the function  at  is all nonpositive numbers () (see Fig. 11).

The graph of the function is in the lower half-plane.

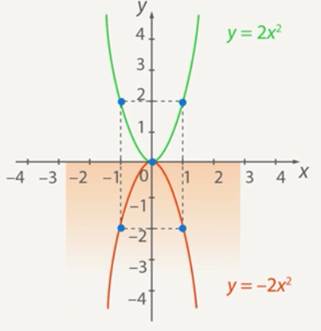
Figure 11. The function  takes non-positive values at 

2. Property 2. The graph  at  is symmetric about the axis  - the function is even ().

3. Property 3. The graph  at  increases for negative  and decreases for positive (see Figure 12).

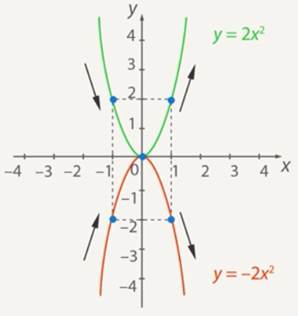
Fig. 12. Decreasing and increasing of the function  at 

4. Transformations of the graph of function  at : the graph narrows as  decreases and widens as  increases (see Fig. 13).

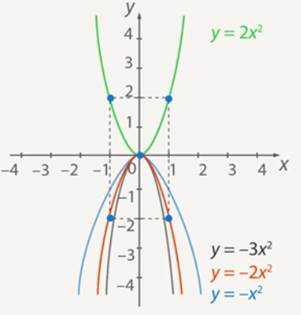
Fig. 13. Transformations of the graph of the function  at 

Problem (k < 0)

At what value of  does the graph of the function  pass through point ? Draw this graph.

Solution

Substitute the coordinates of the point into the equation. We obtain:.

Now plot  (see Fig. 14).

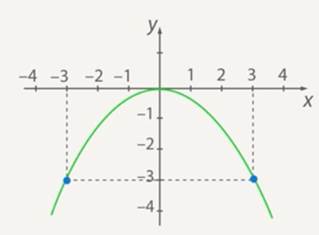
Figure 14. graph of the  function

You can check yourself from the graph - the graph passes through point .

Note that the negativity of the number  was obvious at once: since our function takes a negative value at least at one point, it must be negative.

Answer: .

Solve the equation: .

Solution

Solve this equation graphically by plotting the left and right parts of the equation (see Figure 15):

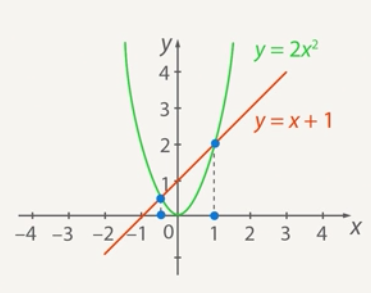
Figure 15. solving the equation graphically

You can see from the graph that this equation has two solutions:  and . Note that if the root of  is easy to see from the graph, then  is more complicated - it is a noninteger. Therefore usually in such cases the hypothesis is made that  is the root, and then the test is performed by substitution.

Answer: .

Conclusion

In this lesson we found out what the graph of the function  looks like and how it changes as  changes. We found out what properties this graph has:

1. value area:  at ,  at .

2. Parity (the graph is symmetric about the  axis).

3. Monotonicity: at  it increases at negative  and decreases at positive; at  it increases at positive  and decreases at negative.

Add comment