Unit conversion

In this lesson we will learn how to convert physical quantities from one unit of measurement to another.

Length unit conversion

We know from past lessons that the basic units of length measurement are:

• millimeters;
• centimeters;
• decimeters;
• meters;
• kilometers.

Any quantity that describes length can be converted from one unit of measure to another.

In addition, when solving problems in physics, it is necessary to use the international system SI. If the length is given not in meters, but in another unit of measurement, then it is necessary to convert it into meters, as the meter is the unit of length in the SI system.

In order to convert length from one unit of measure to another, you need to know what a particular unit of measure consists of. You need to know that, for example, that there are ten millimeters in one centimeter or one kilometer consists of a thousand meters.

Let's show with a simple example how you can reason when converting length from one unit of measure to another. Suppose there are two meters and you want to convert them to centimeters.

First you need to find out how many centimeters there are in one meter. There are one hundred centimeters in one meter:

1 m = 100 cm

If there are 100 centimeters in 1 meter, how many centimeters will be in two meters? The answer is 200 centimeters. And those 200 centimeters is the result of multiplying 2 by 100.

So, to convert 2 meters into centimeters, multiply 2 by 100.

2 × 100 = 200 cm

Now let's try to convert the same 2 meters into kilometers. First we need to find out how many meters there are in one kilometer. One kilometer = one thousand meters:

1 km = 1000 m

If 1000 meters - one kilometer, then a "kilometer" that has only 2 meters will be much smaller. To get it you need to divide 2 by 1000

2 : 1000 = 0.002 km

At first it may be difficult to remember which action to use to convert units - multiplication or division. Therefore, at first it is convenient to use the following rule:

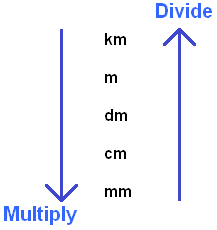
The essence of this rule is that multiplication is applied when converting from a higher unit to a lower one. And vice versa, when converting from a lower unit to a higher one, division is applied.

The arrows pointing down and up indicate that the transition from a higher unit to a lower unit and the transition from a lower unit to a higher unit, respectively. At the end of the arrow it is indicated what operation to apply: multiplication or division.

For example, convert 3000 meters to kilometers using this diagram.

So we have to convert meters to kilometers. In other words, go from a lower unit to a higher one (a kilometer is older than a meter). We look at the diagram and see that the arrow indicating the transition from lower to higher units is pointing upward, and at the end of the arrow it says that we must apply division:

Now we need to find out how many meters are contained in one kilometer. One kilometer - 1000 meters. If you want to find out how many kilometers are 3,000 meters, you should divide 3,000 by 1,000

3000 : 1000 = 3 km

So, when you convert 3000 meters into kilometers, you get 3 kilometers.

Let's try to convert the same 3000 meters into decimeters. Here we have to convert from higher units to lower units (decimeter is lower than meter). We look at the diagram and see that the arrow indicating the transition from higher units to lower units is pointing downward, and at the end of the arrow it says that we must apply multiplication:

Now we need to find out how many decimeters are in one meter. There are 10 decimeters in one meter.

1 m = 10 dm

And to find out how many such decimeters in three thousand meters, you need to multiply 3000 by 10

3000 × 10 = 30000 dm

So when you translate 3000 meters into decimeters, you get 30000 decimeters.

Mass unit conversion

We know from past lessons that the basic units of mass measurement are:

• milligrams;
• grams;
• kilograms;
• hundredweights (centner);
• tons.

Any quantity that characterizes mass can be converted from one unit of measurement to another.

In addition, when solving physics problems, it is necessary to use  the international system SI. That is, if the mass is given not in kilograms, but in another unit of measurement, it is necessary to convert it into kilograms, as the kilogram is the unit of mass measurement in the SI system.

In order to convert mass from one unit of measurement to another, you need to know what that unit of measurement consists of. That is, you need to know that, for example, one kilogram is made up of a thousand grams.

Let's show with a simple example how you should calculate when converting mass from one unit of measurement to another. Suppose there are 3 kilograms and we need to convert them to grams.

First you need to find out how many grams are in one kilogram. One kilogram is one thousand grams:

1 kg = 1000 g

If 1 kilogram - 1000 grams, how many grams will be contained in three such kilograms? The answer can be calculated easily - 3000 grams. And these 3000 grams is the result of multiplying 3 by 1000. So, to convert 3 kilograms to grams, you have to multiply 3 by 1000.

3 × 1000 = 3000 g

Now let's try to convert the same 3 kilograms to tons. First we need to find out how many kilograms there are in one ton. One ton contains one thousand kilograms:

1 t = 1000 kg

If one ton - 1000 kilograms, then a "ton" that contains only 3 kilograms will be much smaller. To get it, divide 3 by 1000

3 : 1000 = 0.003 t

As in the case with the translation of units of length, at first it is convenient to use the following rule:

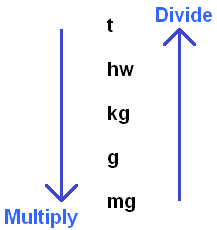
This diagram will allow you to quickly decide what action to perform to convert units - multiplication or division.

For example, let's convert 5000 kilograms to tons using this rule.

So, we have to go from kilograms to tons. In other words, go from a lower unit of measurement to a higher one (a ton is older than a kilogram). We look at the diagram and see that the arrow indicating the transition from lower to higher units is directed upwards and at the end of the arrow it says that we must apply division:

Now we need to find out how many kilograms are contained in one ton. One ton contains 1000 kilograms. And to find out how many tons are 5000 kilograms, divide 5000 by 1000

5000 : 1000 = 5 t

So, when you convert 5000 kilograms to tons, you get 5 tons.

Let's try to convert 6 kilograms to grams. In this case, we are converting from a higher unit to a lower one. Therefore, we will apply multiplication.

First you need to know how many grams there are in one kilogram. One kilogram contains one thousand grams:

1 kg = 1000 g

If 1 kilogram = 1000 grams, then six such kilograms would have six times as many grams. So six must be multiplied by 1000

6 × 1000 = 6000 g

So, if you convert 6 kilograms to grams, you get 6000 grams.

Time units conversion

We know from past lessons that the basic units of time measurement are:

• seconds;
• minutes;
• hours;
• days.

Any quantity that characterizes time can be converted from one unit of measurement to another.

In addition, when solving physics problems, it is necessary to use  the requirements of the international system SI. That is, if time is given not in seconds, but in another unit of measurement, it is necessary to translate it into seconds, as a second is the unit of measurement of time in the SI system.

In order to translate time from one unit of measurement to another, you need to know what a particular unit of time consists of. That is, you need to know that, for example, one hour consists of sixty minutes, or one minute = sixty seconds, etc.

Let us show by a simple example of converting time from one unit of measurement to another. Suppose you want to convert two minutes to seconds.

First you need to find out how many seconds are in one minute. One minute contains sixty seconds:

1 min = 60 s

If there are 60 seconds in one minute, how many seconds are there in two such minutes? The answer is obvious: 120 seconds. And those 120 seconds is the result of multiplying 2 by 60. So, in order to convert 2 minutes into seconds, you need to multiply 2 by 60.

2 × 60 = 120 s

Now let's try to convert the same 2 minutes into hours. Since we convert minutes into hours, we must first find out how many minutes there are in one hour. One hour - sixty minutes:

1 h = 60 m

If one hour = 60 minutes, an hour that contains only 2 minutes will be much less. To get it, divide 2 minutes by 60

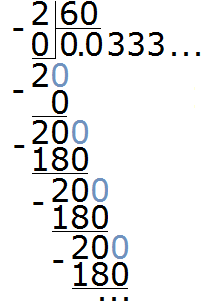
Dividing 2 by 60 results in a periodic fraction of 0.0 (3). This fraction can be rounded to the hundredth place. Then we get the answer 0.03

2 : 60= 0.03 h

When converting units of time measurement, a rule that tells you whether to use multiplication or division is also applicable:

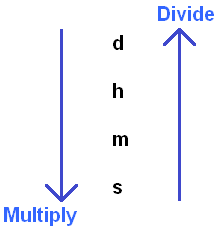
For example, let's convert 25 minutes to hours using this rule.

So, we must convert from minutes to hours. In other words, go from a lower unit to a higher one (hours are older than minutes). We look at the diagram and see that the arrow indicating the transition from lower to higher units is directed upwards, and at the end of the arrow it is indicated that we must apply division:

Now we need to find out how many minutes are contained in one hour. One hour contains 60 minutes. And an hour that contains only 25 minutes will be much less. To find it, divide 25 by 60

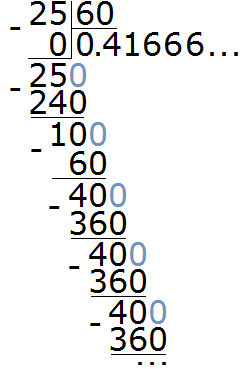
Dividing 25 by 60 results in a periodic fraction of 0.41 (6). This fraction can be rounded to the hundredth place. Then the answer is 0.42

25 : 60 = 0.42 h

Video lesson

Add comment