Here are short articles answering one specific question.
As we know, a decimal consists of a whole part and a fractional part. When adding decimals, the whole and fractional parts are added separately.
For example, let's add the decimals 3.2 and 5.3. It is more convenient to add decimals in columns.
Let's first write these two fractions in a column, making sure the whole parts are under the whole parts and the fractional parts are under the fractional parts. At school, this requirement is called "dot under dot".
Let's write the fractions in a column so that the decimal point is under the point:

Add up the fractional parts: 2 + 3 = 5. Write five in the fractional part of our answer:
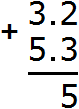
Now add the whole parts: 3 + 5 = 8. Write the eight in the whole part of our answer:
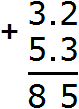
Now separate the whole part from the fractional part with a dot. To do this, again follow the rule "dot under dot":
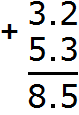
The answer is 8.5. So the expression 3.2 + 5.3 equals 8.5
3.2 + 5.3 = 8.5
In fact, not everything is as simple as it seems at first glance. Here, too, there are pitfalls, which we are now going to talk about.
To add fractions with the same denominators, add their numerators and leave the denominator unchanged.
For example, let's add fractions ![]() and
and ![]() . Add up the numerators and leave the denominator unchanged:
. Add up the numerators and leave the denominator unchanged:
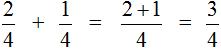
This example can be easily understood if you think of a pizza that is divided into four parts. If you add ![]() pizzas to
pizzas to ![]() pizza, you get
pizza, you get ![]() pizza:
pizza:
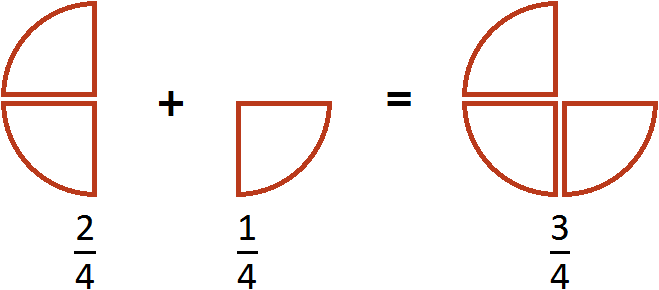
Now let's learn how to add fractions with different denominators. When fractions are added, the denominators of those fractions should be the same. But they are not always the same.
For example, fractions ![]() and
and ![]() can be added together because they have the same denominators.
can be added together because they have the same denominators.
But fractions ![]() and
and ![]() cannot be added together at once because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
cannot be added together at once because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
There are several ways to reduce fractions to the same denominator. Today we will look at just one of them, since the others may seem complicated to a beginner.
The essence of this method is that first we look for the least common multiple (LCM) of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional multiplier is obtained. Do the same with the second fraction - LCM divided by the denominator of the second fraction and get the second additional multiplier.
Then the numerators and denominators of the fractions are multiplied by their additional multipliers. As a result, fractions with different denominators are converted to fractions with the same denominators. And we already know how to add such fractions.
There are problems in which you need to add mixed numbers. For example, to find the value of the expression ![]() . To solve this example, you need to add the whole and fractional parts separately.
. To solve this example, you need to add the whole and fractional parts separately.
First, let's write down the mixed numbers in expanded form:
![]()
Apply the combinative law of addition. Group the whole and fractional parts separately:
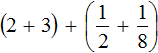
Let's calculate the integers: 2 + 3 = 5. In the main expression, replace the expression in parentheses (2 + 3) with the resulting five:
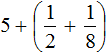
Now let's calculate the fractional parts. This is the addition of fractions with different denominators. We already know how to add such fractions:
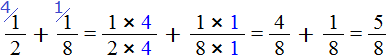
You may encounter problems where you need to add a whole and a mixed number. For example, add 2 and a mixed number ![]() . In this case, the whole parts are added separately, and the fractional part is left unchanged:
. In this case, the whole parts are added separately, and the fractional part is left unchanged:
![]()
Here the mixed fraction ![]() was expanded as part of the solution, then the whole parts were grouped and added together. At the end the whole and fractional parts were folded. The result was the answer
was expanded as part of the solution, then the whole parts were grouped and added together. At the end the whole and fractional parts were folded. The result was the answer ![]() .
.
Let's try to represent this solution in the form of a picture. If you add three whole pizzas and a third of a pizza to two whole pizzas, you get five whole pizzas and a third of a pizza:
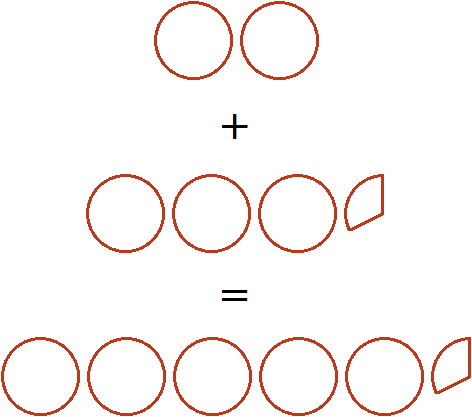
You may encounter problems in which you need to add a whole number and a fraction. For example, add a number 2 and a fraction![]() . To solve this example, you need to represent the number 2 as a fraction
. To solve this example, you need to represent the number 2 as a fraction ![]() . Then add fractions with different denominators:
. Then add fractions with different denominators:
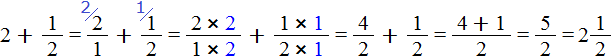
Now look carefully at this example. Let's look at the beginning and the end of it. Its beginning looks like this: ![]() , and the end is this:
, and the end is this: ![]() . The difference is that in the first case the number 2 and the fraction
. The difference is that in the first case the number 2 and the fraction ![]() are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that
are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that ![]() is a convolute form of a mixed number, and
is a convolute form of a mixed number, and ![]() is an expanded form.
is an expanded form.
When we have a mixed number of the form ![]() in front of us, we must realize that the addition sign is omitted.
in front of us, we must realize that the addition sign is omitted.
Consider the sum of three summands:
2 + 3 + 5
To calculate this expression, you can first add the numbers 2 and 3 and add the result to the number 5. For convenience, the sum of numbers 2 and 3 can be placed in parentheses, indicating that this sum will be calculated first:
Definition. The associative law of multiplication says that there is no matter how you group numbers you are multiplying together.
Consider the following expression:
2 × 3 × 4
This expression can be calculated in any order. First you can multiply the numbers 2 and 3, and multiply the result by 4:
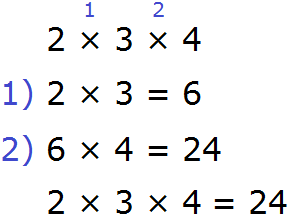
Or you can first multiply the numbers 3 and 4, and multiply the result with the number 2
Calculate the fraction![]() . Five divided by two will be two and one in the remainder:
. Five divided by two will be two and one in the remainder:
5 : 2 = 2 (1 in the remainder)
Verification: (2 × 2) + 1 = 4 + 1 = 5
But now we are dealing with fractions, so we have to answer in fractional form. To get a good understanding of how to do this, let's look at an example from life.
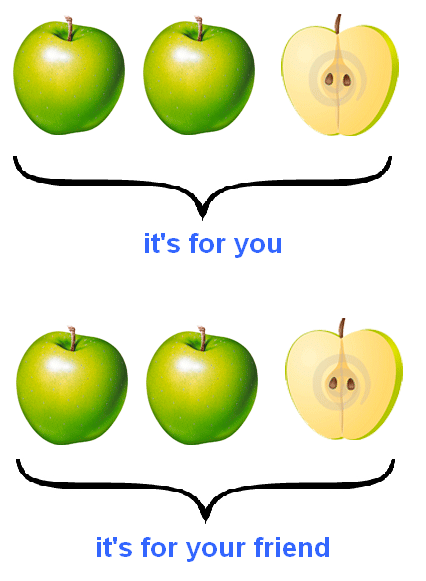
Imagine you have five apples and decide to share them with your friend. And share them fair and square, so that everyone gets the same. How do you divide these five apples?
Obviously, each of you will get two apples, and you will cut the remaining one apple in half with a knife and divide it among yourselves as well:
Definition. The commutative law of addition says that it doesn't matter what order you add up numbers.
Indeed, add a five to a two and you get a seven. And vice versa, add a two to a five and you get a seven again:
5 + 2 = 7
2 + 5 = 7
If we put 10 kilograms of apples in one bag and put 10 kilograms of apples in other bag, bags will be equal, and it does not matter that the apples in the bags are mixed in a random way. If we take the bag from the scales and mix the apples in it like balls in a lottery bag, the bag will still weigh 10 kilograms. The sum will not change from rearranging the summands. The summands in this case are apples, and the sum is the total weight.
Definition. The commutative law of multiplication says that it doesn't matter what order you multiply variables or numbers. Let's see if this is true.
Multiply a five by a two and then vice versa by a two by a five.
5 × 2 = 10
2 × 5 = 10
Page 1 of 9