Basic Laws of Math

There are rules in our lives that we must obey. Following the rules guaranteesa a peaceful and carefree life. When you don't obey laws, it leads to unfortunate consequences.

Mathematics has its own laws that must also be followed. Failure to follow the laws of mathematics will at best result in lower grades, and at worst will result in planes falling, computers freezing, roofs flying off due to high winds, poor communication, and similar bad things.

The laws of mathematics consist of simple properties. These properties are familiar to us from school. But it doesn't hurt to remember them again, or, better yet, to write them down and learn them by heart.

In this lesson we will look at only a small part of the laws of mathematics. They will be enough for us to study mathematics further.

Commutative Law of Addition

Definition. The commutative law of addition says that it doesn't matter what order you add up numbers.

Indeed, add a five to a two and you get a seven. And vice versa, add a two to a five and you get a seven again:

5 + 2 = 7

2 + 5 = 7

If we put 10 kilograms of apples in one bag and put 10 kilograms of apples in other bag, bags will be equal, and it does not matter that the apples in the bags are mixed in a random way. If we take the bag from the scales and mix the apples in it like balls in a lottery bag, the bag will still weigh 10 kilograms. The sum will not change from rearranging the summands. The summands in this case are apples, and the sum is the total weight.

Thus, the expressions 5 + 2 and 2 + 5 can be equated. This would mean that their sum is equal:

5 + 2 = 2 + 5

7 = 7

We assume that you have learned one of the previous lessons, which was called expressions, so we will write down the commutative law of addition using variables:

a + b = b + a

This commutative law of addition will work for any numbers. For example, take any two numbers. Let a = 2, b = 3. We have assigned the variables a and b with values 2 and 3. These values will go into the main expression a + b = b + a and substitute where needed. Number 2 will be substituted for a, number 3 will be substituted for b

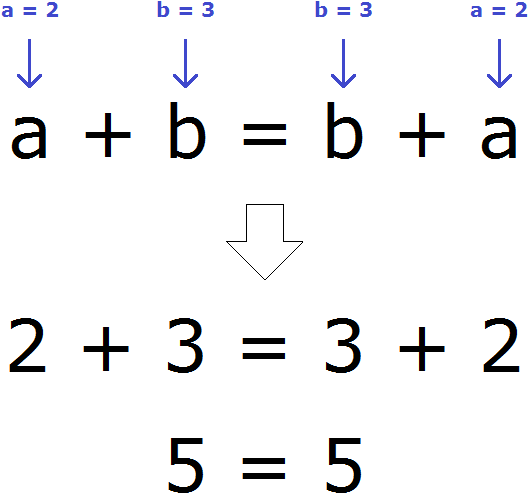
Associative Law of Addition

Consider the sum of three summands:

2 + 3 + 5

To calculate this expression, you can first add the numbers 2 and 3 and add the result to the number 5. For convenience, the sum of numbers 2 and 3 can be placed in parentheses, indicating that this sum will be calculated first:

2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10

Or you can add the numbers 3 and 5, then add the result to the number 2

2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10

You can see that in both cases you get the same result.

Thus, between the expressions (2 + 3) + 5 and 2 + (3 + 5) we can put an equal sign, because they are equal to the same value:

(2 + 3) + 5 = 2 + (3 + 5)

10 = 10

Let's write down the associative law of addition using variables:

(a + b) + c = a + (b + c)

Commutative law of multiplication

Definition. The commutative law of multiplication says that it doesn't matter what order you multiply variables or numbers. Let's see if this is true.

Multiply a five by a two and then vice versa by a two by a five.

5 × 2 = 10

2 × 5 = 10

In both cases you get the same result, so you can put an equal sign between the expressions 5 × 2 and 2 × 5 because they are equal to the same value:

5 × 2 = 2 × 5

10 = 10

Let's write down the commutative law of multiplication using variables:

a × b = b × a

It is not necessary to use the letters a and b to write laws as variables. Any other letters can be used, e.g. c and d or x and y. The same commutative law of multiplication can be written as follows:

x × y = y × x

Associative law of multiplication

Definition. The associative law of multiplication says that there is no matter how you group numbers you are multiplying together.

Consider the following expression:

2 × 3 × 4

This expression can be calculated in any order. First you can multiply the numbers 2 and 3, and multiply the result by 4:

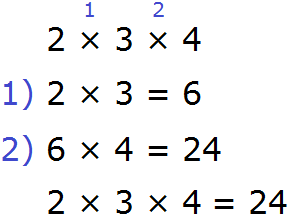
Or you can first multiply the numbers 3 and 4, and multiply the result with the number 2

Thus, between the expressions (2 × 3) × 4 and 2 × (3 × 4) we can put an equal sign, because they are equal to the same value:

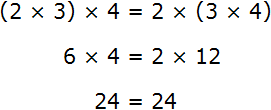
Let's write down the combinative law of multiplication using variables:

a × b × c = (a × b) × c = a × (b × c)

Example 2. Find the value of the expression 1 × 2 × 3 × 4

This expression can be calculated in any order. Let us calculate it from left to right in the order of actions:

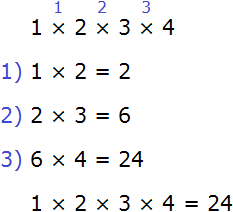
Distributive law of multiplication

Definition. The distributive law of multiplication says that any number which is multiplied by the sum of two or more numbers is equal to the sum of that number multiplied by each of the numbers separately.

Consider the following expression:

(3 + 5) × 2

We know that we must first perform the action in parentheses. We do it:

(3 + 5) = 8

In the main expression (3 + 5) × 2, replace the expression in parentheses with the resulting eight:

8 × 2 = 16

The answer is 16. The same example can be solved using the distributive law of multiplication. To do this, multiply each summand in parentheses by 2, then add the results:

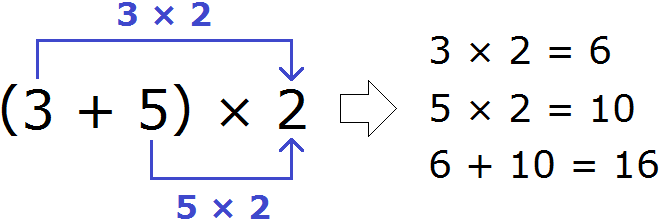
We have looked at the distributive law of multiplication in too much detail. At school, this example would have been recorded very briefly. You need to get used to this kind of notation, too. It looks like this:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

Or even shorter:

(3 + 5) × 2 = 6 + 10 = 16

Now let's write down the distributive law of multiplication using variables:

(a + b) × c = a × c + b × c

Let's look carefully at the beginning of this distributive law of multiplication. Its beginning looks like this: (a + b) × c.

If we consider the expression in parentheses (a + b) as a whole, it will be a multiplier, and the variable c will be a multiplier because they are connected by the multiplication sign ×

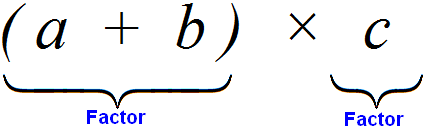
From the commutative law of multiplication we learned that if we swap the first factor and the second, the product does not change.

If we swap the factor (a + b) and the factor c, we get the expression c × (a + b). Then we multiply the variable c by the sum of (a + b). To do this multiplication, we apply the distributive law of multiplication. In this case, the variable c must be multiplied by each summand in parentheses:

c × (a + b) = c × a + c × b

Example 2. Find the value of the expression 5 × (3 + 2)

Multiply the number 5 by each summand in parentheses and add the results:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Example 3. Calculate 6 × (5 + 2)

Multiply 6 by each summand in parentheses and add the results:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

If the parentheses are not the sum but the difference, you must first multiply the multiplier by each number that is in the parentheses. Then subtract the second number from the first number. In principle, there is nothing new.

Example 4. Find the value of the expression 5 × (6 - 2)

Multiply 5 by each number in parentheses. Then subtract the second number from the first number:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Example 5. Calculate 7 × (3 - 2)

Multiply 7 by each number in parentheses. Then subtract the second number from the first number:

7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7

Exercises

Task 3. Find the value of the expression using the order of operations:

4 × (5 + 4) + 9 × (3 + 2)

Solution:

Show Solution

Add comment